饱和状态下黄绵土坡面细沟侵蚀可蚀性和临界剪切应力特征

黄钰涵，杨梦格，雷廷武，李法虎，王 伟

饱和状态下黄绵土坡面细沟侵蚀可蚀性和临界剪切应力特征

黄钰涵1,2，杨梦格2，雷廷武1※，李法虎1，王 伟3

（1. 中国农业大学水利与土木工程学院，北京 100083；2. 广西大学林学院，广西森林生态与保育重点实验室，南宁 530004；3. 中国农业大学工学院，北京 100083）

土壤可蚀性参数和临界剪切应力是评价土壤易侵蚀程度和抗水流剪切变形能力的重要指标，目前在黄绵土坡面细沟侵蚀过程中，土壤饱和条件下可蚀性参数和临界剪切应力的变化尚不明确。该研究采用室内土槽模拟冲刷试验确定不同坡度（5°、10°、15°、20°）和流量（2、4、8 L/min）下饱和黄绵土坡面的最大细沟剥蚀率，基于数值法、修正数值法和解析法计算土壤可蚀性参数和临界剪切应力。结果表明，3种方法所得最大细沟剥蚀率均随坡度和流量增加而增大，其中修正数值法和解析法计算的最大细沟剥蚀率更接近。土壤可蚀性参数分别是0.470、0.278和0.256 s/m，土壤临界剪切应力分别为1.502、1.306和1.367 N/m2。修正数值法可提高数值法近似计算的精度，使近似计算结果更接近解析法计算获得的理论值。饱和较未饱和黄绵土的土壤可蚀性参数略有减小（16.83%），而临界剪切应力减小了66.97%，表明土壤饱和对黄绵土土壤可蚀性参数影响很小，但大幅度削弱了土壤临界剪切应力，使得黄绵土坡面饱和后土壤侵蚀更为强烈。此外，饱和黄绵土边坡的临界剪切应力与饱和紫色土坡面相比差异不大，而细沟可蚀性参数大2.26倍，表明土壤饱和对2种土壤临界剪切应力影响程度相似，但黄绵土较紫色土对土壤侵蚀的敏感性更高。研究结果可为饱和状态下不同土壤坡面细沟侵蚀模型参数的优化提供参考。

土壤；侵蚀；细沟；可蚀性；临界剪切应力；饱和；最大细沟剥蚀率

0 引 言

细沟侵蚀是坡面侵蚀泥沙的重要来源，是坡面侵蚀泥沙运移的主要通道。侵蚀细沟形成后，土壤侵蚀显著增加，土地退化加剧，严重威胁农业可持续发展[1-3]，因此，研究者们对土壤侵蚀预报和土壤侵蚀控制措施持续关注[4]。目前，常用的土壤侵蚀预报模型包括：经验模型（Universal Soil Loss Equation (USLW)和Revised Universal Soil Loss Equation (RUSLE)）、基于物理过程的预报模型（Water Erosion Prediction Project (WEPP)和European Soil Erosion Model (EUROSEM)）、分布式流域水文模型（Soil and Water Assessment Tool (SWAT)）等[5-6]。土壤可蚀性参数和临界剪切应力是土壤侵蚀预报模型的2个重要参数，其中，土壤可蚀性是指土壤是否易受侵蚀破坏的性能, 即土壤对侵蚀介质剥蚀和搬运的敏感性[7]；土壤的临界剪切应力是表征土体力学性质的一个主要指标，它的大小与土壤凝聚力和内摩擦角有关，可直接反映土体抵抗外力作用发生剪切变形破坏的能力[7]。因此，这2个参数是评价土壤易侵蚀程度和抗水流剪切变形能力的重要指标[8-9]。

土壤可蚀性参数与临界剪切应力作为土壤坡面细沟侵蚀模型的重要参数，实现其精确计算对提高细沟侵蚀模型精度有十分重要的意义。研究发现影响土壤可蚀性参数和临界剪切应力的因素包括：土壤含水量[10-12]、土壤水势梯度[13]、有机质含量[14]、坡度、水流流量[7]、土壤孔隙水压力[13,15-16]、土壤孔隙比[17]等。其中，土壤含水量的影响越来越受到关注，Hanson等[10]发现土壤抗侵蚀能力随着土壤含水量的增加在土壤塑限范围内升高。Su等[15]发现随着土壤水文条件的变化（从排水到饱和再到渗流状态下），不同土壤类型（黄褐土、紫色土、干红壤）的土壤可蚀性参数逐渐增加，而临界剪切应力没有显著变化。Nouwakpo等[13]发现土壤渗流状态下临界剪切应力随垂直水力梯度的增加呈线性减小趋势，导致土壤侵蚀加剧。邢行等[12]通过限定性细沟模拟试验指出，土壤水分含量变化会引起土壤临界剪切应力的变化，这与Singh等[11]研究小流域土壤侵蚀得出的试验结果一致。以上研究均表明土壤含水量不同能引起近地表水文状况显著变化，进而引发不同程度的土壤侵蚀。土壤饱和作为一种特殊的近地表水文状况，显著影响了土壤团聚体结构、土壤孔隙水压力和表面粗糙程度等[18]，进而改变土壤侵蚀。目前关于土壤饱和的研究主要集中于坡面产流产沙过程[19-22]及土壤力学性质方面[23-25]，而针对饱和土壤坡面土壤可蚀性参数和临界剪切应力的研究较少，开展相关研究可为完善土壤侵蚀预报模型提供科学依据。

黄土高原地区每年60%～70%的降雨量集中于夏季，降雨具有短历时、高强度的特点[26]。极端降雨条件下，可能因犁底层入渗受阻，使耕层逐渐形成饱和土层，加剧土壤流失。黄绵土作为黄土高原分布面积最大的土壤类型，是受强降雨影响形成农地耕作层饱和土壤侵蚀的核心区域之一，因此针对黄土区坡耕地饱和状态下黄绵土边坡的土壤侵蚀研究显得尤为重要。本文研究黄绵土坡面饱和对土壤可蚀性参数和临界剪切应力的影响，并对比了黄绵土与紫色土的差异，以期为饱和状态下土壤坡面细沟侵蚀模型参数的优化提供科学基础。本文主要研究内容如下：1）根据室内试验细沟剥蚀率数据集，运用数值法、修正数值法和解析法计算饱和黄绵土的细沟可蚀性参数和临界剪切应力；2）根据解析法精确计算的理论值，明确数值法与修正数值法的计算精度；3）对比饱和与未饱和状态下黄绵土坡面及饱和状态下黄绵土与紫色土的土壤可蚀性参数与临界剪切应力。

1 材料与方法

1.1 供试土壤

试验土壤为黄绵土，采集自中国科学院水利部水土保持研究所安塞水土保持综合试验站（36°51′30″N、109°19′23″E）周边的退耕荒地，该区域为典型梁茆状黄土丘陵沟壑区。将收集的土壤风干后过4 mm筛，使用Mastersizer 3000激光粒度分析仪（Malvern, UK, ±1%）测定试验土壤机械组成结果如下：砂粒、粉粒和黏粒体积分数分别为23.80%、64.57%和11.63%，根据美国制土壤质地分类标准试验土壤为粉壤土。通过重铬酸钾法测得有机质含量为4.5 g/kg。

1.2 试验设计与数据集

试验在中国农业大学水利与土木工程学院模拟降雨大厅进行，试验土槽为钢制可调节坡度土槽，长8 m、宽1.2 m。用钢板将土槽中间隔成8个8 m×0.1 m×0.35 m的限定性沟槽，即8条细沟，每条细沟长度为8 m，宽度0.1 m，深度0.25 m。在最左和最右侧预留出0.2 m设置饱和土壤装置，隔板间及隔板与试验平台的间隙用黏质土壤填充压实5 cm厚，用于模拟犁底层，填土容重为1.5 g/cm3。

供试土槽的8条细沟以1 m为间隔等分为8条沟段,每米沟段的底部都压实填充3 cm厚的黏土层，并在每米沟段的黏土层上方水平设置1根水管，每根水管位于每米沟段前端10 cm处，且贯穿8条细沟（图1a）。每个0.1 m沟段间隔的渗水管上表面布设3个渗水孔（直径2 mm），渗水孔的间距为20 mm，在安装时渗水孔朝上坡方向放置。自渗水管向下游0.9 m长都用黏性土壤填充压实2 cm，土壤容重为1.5 g/cm3，每米沟段的前部0.1 m采用粗砂填充2 cm并覆盖渗水管，作为渗水单元向供试土壤中供水（图1b）。渗水管上部为供水管，每个供水管上安装阀门控制供水水量，8根供水管末端都共同连接至1根输水管，将水流分别输送至各供水管。此外，在8条细沟中均铺设渗水良好的土工织物以保护底部沙层，填入20 cm厚的供试土壤并自然沉降。

图1 试验装置图

试验工作原理为水流通过输水管进入供水管而后到达渗水管，并通过渗流孔进入沙层直至沙层达到饱和，而后水流持续向上饱和供试土壤，并逐渐向下游推进，最终实现全坡面土壤供水直至完全饱和。根据中国农耕地的坡度最高25°，且据已有研究[27]以及野外坡耕地调研，细沟发育的临界坡度为2°，且在5°以上发育最为广泛，因此试验选取缓斜坡、斜坡与陡坡的代表性坡度，设置4个坡度：5°、10°、15°、20°。根据以往研究[28]得出的黄绵土坡耕地产生细沟侵蚀的临界流量及黄绵土细沟侵蚀研究中采用的人工模拟降雨强度进行换算，同时为了与前人研究[4]体系保证统一以便对比，因此，本文设计3个流量：2、4、8 L/min。当供试土壤完全饱和后，调节坡度与流量测定细沟侵蚀水流流速与沿程含沙水样浓度，且试验开始前供水条件保持不变。采用电解质示踪法测量（1、2、3、4、5、6、7、8 m）的水流流速，并取平均流速作为不同水力工况条件下的水流流速（表1）[29]。另外，沿程测定含沙水样浓度：分别从距离细沟出口的1、2、4、8 m处用4个300 mL容积的钢杯收集泥沙水流样品，采样时间为30～60 s。每个设计工况条件下，水流流速测量与沿程水流含沙量冲刷试验均各重复3次。之后将样品静置24 h后滤掉上层清液，放入105 ℃烘箱中烘干48 h，称质量记录并计算水流含沙量，并通过数值法、修正数值法和解析法分别计算得到细沟剥蚀率。

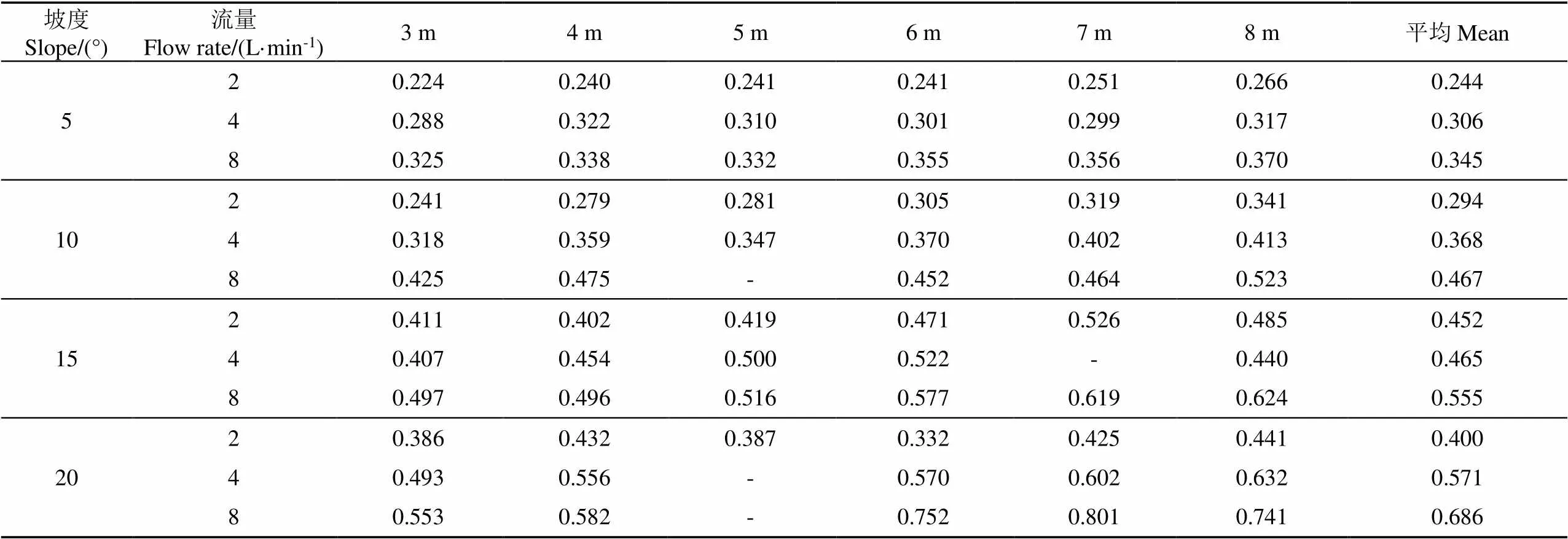
表1 不同水力工况条件下饱和黄绵土坡面沿程水流流速[29]

1.3 计算原理

在WEPP模型中细沟剥蚀率可用式（1）表示：

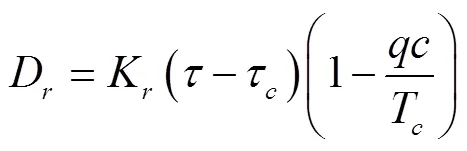
式中D是细沟剥蚀率，kg/(m2·s)；K是土壤可蚀性参数，s/m；是水流剪切应力，N/m2；τ是临界剪切应力，N/m2；为单宽流量，m3/(s·m)；为水流含沙量，kg/m3；T为水流输沙能力，kg/m3。在饱和土壤坡面上，清水中的含沙量为0，即水流刚刚进入细沟沟头时细沟剥蚀率可视为最大值，因此由式（1）可得饱和土壤坡面最大细沟剥蚀率为

式中D(max)为饱和土壤坡面的最大细沟剥蚀率，kg/(m2·s)。由式（2）可知，确定不同设计试验工况下最大细沟剥蚀率与水流剪切应力，就可通过拟合分析得到细沟可蚀性参数与临界剪切应力。

1.3.1 数值法

根据细沟剥蚀率定义，细沟剥蚀率是细沟沟长的函数，且不随时间变化[30]。基于质量守恒定律，在细沟剥蚀阶段水流输沙量的增量应与土壤剥蚀量相等，则对应的饱和土壤坡面细沟剥蚀率可用数值法近似计算获得[31]，即：

式中为细沟沟长，m；为水流流量，m3/s；，为细沟沟宽，m；Δ为细沟沟宽增量，m；为单宽流量，m3/(s·m)，D1为数值法计算的细沟剥蚀率，kg/(m2·s)。已有研究表明[31]，饱和土壤坡面上细沟剥蚀率数值计算结果与水流含沙量有良好的线性函数关系，如式（4）：

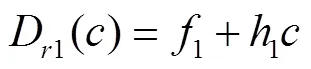
式中1为常数，kg/(m2∙s)；1为比例系数，一般为负值，表示随水流含沙量增加细沟剥蚀率下降的速率，m/s。从式（4）中可看出在饱和土壤坡面上水流的细沟剥蚀率随水流含沙量的增大而呈线性减小。当水流含沙量为0时，细沟剥蚀率可达到其最大值。

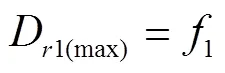
式中D1(max)为数值法计算的饱和土壤坡面最大细沟剥蚀率，kg/(m2·s)。

1.3.2 修正数值法

根据Huang等[32]获得饱和土壤坡面细沟侵蚀过程中水流含沙量与细沟沟长的变化关系。

式中为水流达到输沙能力时的最大水流含沙量，kg/m3；为随细沟沟长增速的衰减系数，m-1。

由于数值法为近似计算，因此数值法计算获得的细沟剥蚀率与真实值存在较大误差。式（6）为单调增函数，且根据1.3.1节所述细沟剥蚀率数值计算原理，基于数学理论，总能在（x-1, x）区间上找到一点(ξ)使得式（7）成立。

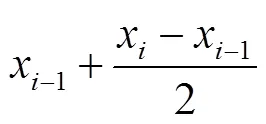
式中D2为修正数值法计算的饱和土壤坡面细沟剥蚀率，kg/(m2∙s)；c-1和c分别表示细沟沟段内第-1和处水流含沙量，kg/m3。修正数值法可提高沿程细沟剥蚀率的计算精度，为后续的细沟侵蚀参数估算及模型构建提供基础。采用修正数值法计算细沟剥蚀率与水流含沙量间的关系，如式（9）所示：

式中2为常数，kg/(m2∙s)；2为式（9）中的比例系数，表示随水流含沙量增加细沟剥蚀率下降的速率，m/s。从式（9）可看出，当水流含沙量为0时细沟剥蚀率可达到其最大值，如式（10）：

式中D2(max)为修正数值法计算的饱和土壤坡面最大细沟剥蚀率，kg/(m2∙s)。

1.3.3 解析法

如式（3）所示，根据细沟剥蚀率的定义，当∆趋近于0时，∆/2也趋近于0。因此，根据极限的基本原理对式（3）进行转换：

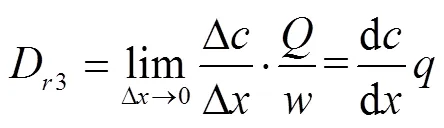
式中D3为解析法计算的饱和土壤坡面细沟剥蚀率(kg/(m2∙s))，即依据数学原理精确计算所得的理论细沟剥蚀率。式（11）定义了解析法计算饱和土壤坡面细沟剥蚀率，因此将式（6）代入式（11）中可获得通过细沟沟长解析计算细沟剥蚀率的式子，如下：

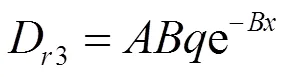
式中D3为通过细沟沟长解析计算的饱和土壤坡面细沟剥蚀率，kg/(m2∙s)；是饱和土壤坡面测量最大水流含沙量，kg/m3；为相关系数m-1，表明细沟剥蚀率随细沟沟长增加而降低的速率。采用解析法计算细沟剥蚀率与水流含沙量间的关系，如式（13）所示：

式中3为常数，kg/(m2∙s)；3为式（13）中的比例系数，表示随水流含沙量增加细沟剥蚀率下降的速率，m/s。由式（13）可知，当水流含沙量为0时，细沟剥蚀率可达到其最大值，如式（14）：

式中D3(max)为解析法计算的饱和土壤坡面最大细沟剥蚀率，kg/(m2∙s)。

将式（2）分别代入式（5）、式（10）与式（14），可计算得到基于3种计算方法的饱和土壤坡面细沟侵蚀土壤可蚀性参数K和土壤临界剪切应力τ：

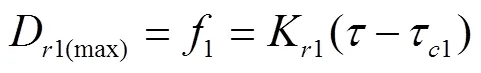
式中K1是基于数值法拟合的土壤可蚀性参数，s/m；τ1是基于数值法拟合的临界剪切应力，N/m2；K2是基于修正数值法拟合的土壤可蚀性参数，s/m；τ2是基于修正数值法拟合的临界剪切应力，N/m2；K3是基于解析法拟合的土壤可蚀性参数，s/m；τ3是基于解析法拟合的临界剪切应力，N/m2。水流剪切应力（τ）为

式中是水的重力密度，9 800 N/m3；为地表坡度的正弦值；avg是侵蚀细沟的水流流速，m/s。

2 结果与分析

2.1 基于3种方法的土壤可蚀性参数与临界剪切应力

基于WEPP模型原理，最大细沟剥蚀率是计算土壤可蚀性参数与临界剪切应力的基础。通过式（5）、式（10）和式（14）得出不同水力工况条件下数值法、修正数值法和解析法计算的最大细沟剥蚀率，如表2所示，3种方法所得结果在坡度为5和10°，流量为2 L/min时都较小，但在坡度为15°和20°，流量为4和8 L/min时逐渐增大。随坡度增加，数值法计算的最大细沟剥蚀率明显高于修正数值法和解析法，即数值法计算的最大细沟剥蚀率对于坡度更加敏感。例如流量为8 L/min时，坡度从10°变化至15°，数值法计算的最大细沟剥蚀率变化率为288.1%，而修正数值法与解析法计算的最大细沟剥蚀率变化率仅为156.0%和151.5%。而在同一坡度下，流量增加对3种方法计算的最大细沟剥蚀率的影响无明显差异。整体来看，修正数值法和解析法计算的最大细沟剥蚀率更接近。

表2 数值法、修正数值法和解析法计算的最大细沟剥蚀率

根据最大细沟剥蚀率结果，运用式（18）计算获得不同水力工况条件下的水流剪切应力，并根据式（15）、（16）和（17）分别进行线性回归，所得结果如图2所示。图2a中直线的斜率即为基于数值法的土壤可蚀性参数0.470 s/m，图2b中直线的斜率即为基于修正数值法的土壤可蚀性参数0.278 s/m，图2c中直线的斜率即为基于解析法的土壤可蚀性参数0.256 s/m。当最大细沟剥蚀率为0时，此时水流剪切力即为临界剪切应力，因此基于数值法计算的临界剪切应力为1.502 N/m2，基于修正数值法的临界剪切应力为1.306 N/m2，基于解析法的临界剪切应力为1.367 N/m2。

将3种方法计算的饱和黄绵土坡面设计水力工况条件下土壤可蚀性参数及临界剪切应力的结果进行对比，发现修正数值法与解析法计算的土壤可蚀性参数（0.278、0.256 s/m）和临界剪切应力（1.306、1.367 N/m2）较为接近，数值法计算的土壤可蚀性参数较大（0.470 s/m、1.502 N/m2）。可见修正数值法较大程度提高了由实测数据近似计算细沟剥蚀率的准确性，使其与解析法计算获得的理论细沟剥蚀率更为接近，从而提高了基于最大细沟剥蚀率计算所得土壤可蚀性参数和临界剪切应力的精度。

图2 基于数值法、修正数值法和解析法计算不同水力工况条件下最大剥蚀率与水流剪切应力的关系

2.2 饱和与未饱和黄绵土坡面细沟侵蚀的土壤可蚀性参数与临界剪切应力对比

本课题组在前期研究中相同试验条件获得了基于解析法计算的未饱和黄绵土坡面土壤可蚀性参数与临界剪切应力[4]。将之与本研究中基于修正数值法和解析法计算的饱和黄绵土坡面细沟侵蚀土壤可蚀性参数及临界剪切应力进行对比，如表3所示。

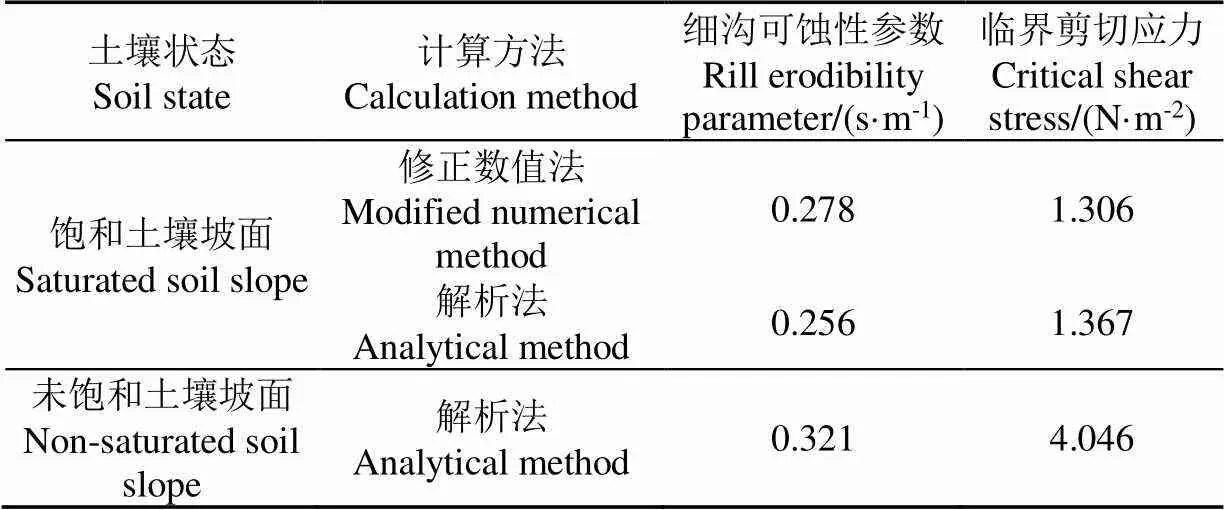
表3 饱和与未饱和黄绵土坡面土壤可蚀性参数与土壤临界剪切应力

如表3所示，饱和黄绵土坡面修正数值法与解析法计算所得土壤可蚀性参数分别较未饱和黄绵土坡面解析法计算土壤可蚀性参数结果小13.40%和20.25%，平均上小16.83%，但饱和黄绵土坡面修正数值法与解析法计算的临界剪切应力分别较未饱和黄绵土坡面解析法计算的临界剪切应力小67.72%和66.21%，平均小66.97%。说明尽管饱和黄绵土坡面细沟侵蚀过程中泥沙输送能力和细沟水流含沙浓度比未饱和黄绵土坡面大[22,32]，但对于给定类型的土壤，土壤可蚀性参数是一个较为稳定的值[14,34]，土壤饱和对土壤可蚀性参数的影响小，但对临界剪切应力影响大。一方面，土壤饱和导致土壤颗粒之间黏结力减弱，土壤团聚体易分解为单颗粒，使得土壤强度显著降低，致使土壤抵抗径流剪切的能力降低[29,35]；另一方面，土壤饱和使得土壤颗粒间隙在孔隙水压力影响下增大，且颗粒间的摩擦显著减小，从而导致土壤的临界剪切应力降低[16]。因此，饱和与未饱和状态下的黄绵土临界剪切应力相差较大，也是饱和黄绵土坡面细沟侵蚀输沙量更大的原因。上述结果表明，土壤饱和主要导致了黄绵土抵抗径流剪切破坏的能力大幅度降低，从而使得黄绵土坡面饱和后更易发生细沟侵蚀。

2.3 饱和黄绵土与紫色土坡面细沟侵蚀的土壤可蚀性参数与临界剪切应力对比

前期研究[2]基于修正数值法和解析法计算得到饱和紫色土坡面细沟剥蚀率，之后通过最大细沟剥蚀率与水流剪切应力回归分析，获得饱和紫色土坡面在相同坡度与流量条件下的土壤可蚀性参数和临界剪切应力。与本文研究结果对比（表4），分析得出饱和状态下黄绵土坡面解析法与修正数值法计算所得土壤临界剪切应力分别比紫色土坡面大4.68%和小2.10%，整体差异不大。但饱和黄绵土坡面解析法与修正数值法计算所得土壤可蚀性参数分别比紫色土坡面大2.16倍和2.35倍，平均大2.26倍。原因可能是黄绵土粉粒含量高、有机质含量低，而紫色土黏粒含量高、有机质含量高，且有研究表明黏粒和有机质含量越高，土壤可蚀性参数越小[14,36]。此外，黄绵土黏聚力低，黏结性差，土壤剖面结构不良，使得黄绵土容易侵蚀；而紫色土通常是丰富的不完全风化粗土块，不易被侵蚀。因此，2种土壤在饱和状态下，黄绵土较紫色土更易分散为小颗粒，易发生侵蚀[37]，黄绵土的土壤可蚀性参数显著高于紫色土。黄绵土与紫色土在饱和状态下的临界剪切应力相近，但土壤可蚀性参数相差较大，说明土壤类型更大程度上决定了土壤可蚀性参数，因此土壤饱和对其他土壤类型的土壤可蚀性参数和临界剪切应力影响值得进一步探究。

表4 饱和状态下黄绵土与紫色土的土壤可蚀性参数与临界剪切应力

3 结 论

本文基于饱和黄绵土坡面细沟侵蚀水流流速与沿程含沙量试验，采用数值法、修正数值法和解析法计算不同水力工况条件下细沟剥蚀率，获得最大细沟剥蚀率，而后通过最大细沟剥蚀率与水流剪切应力的线性回归获得饱和黄绵土坡面细沟侵蚀的土壤可蚀性参数和临界剪切应力，结果表明：1）3种方法所得土壤可蚀性参数分别是0.470、0.278和0.256 s/m，临界剪切应力分别为1.502、1.306和1.367 N/m2。修正数值法可提高数值法近似计算的精度，使近似计算结果更接近解析法计算获得的理论值。2）饱和状态下黄绵土坡面细沟侵蚀的土壤可蚀性参数较与未饱和土壤平均减小16.83%，临界剪切应力相较于未饱和黄绵土坡面平均减小66.97%；说明同一土壤类型的坡面在饱和前后土壤可蚀性参数相近，但临界剪切应力变化较大，土壤饱和极大影响了临界剪切应力，从而使得黄绵土坡面饱和时更易发生细沟侵蚀。3）对不同饱和土壤而言，饱和状态下黄绵土坡面的临界剪切应力与紫色土差异不大，而土壤可蚀性参数比紫色土大2.26倍，说明2种土壤在饱和状态下的临界剪切应力相近，但土壤可蚀性参数相差较大，即土壤类型对土壤可蚀性参数起决定性作用。土壤饱和使得临界剪切应力降低导致土壤坡面细沟侵蚀加剧，且不同土壤类型坡面的土壤可蚀性参数与临界剪切应力受饱和状态的影响不同，因此进一步探究土壤饱和对不同土壤类型土壤坡面的影响可为完善土壤侵蚀预报物理模型提供科学依据。

[1] Chen X Y, Zhao Y, Mi H X, et al. Estimating rill erosion process from eroded morphology in flume experiments by volume replacement method[J]. Catena, 2016, 136: 135-140.

[2] Li D D, Chen X Y, Han Z, et al. Determination of rill erodibility and critical shear stress of saturated purple soil slopes[J]. International Soil and Water Conservation Research, 2021, 10(1): 38-45.

[3] 赵宇辉，张建军，于洋，等. 晋西黄土区蔡家川小流域切沟的空间分布及形态特征[J]. 农业工程学报，2022，38(4)：151-158.

Zhao Yuhui, Zhang Jianjun, Yu Yang, et al. Spatial distribution and characteristics of the gullies in Caijiachuan watershed in loess region of Western Shanxi Province, China[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2022, 38(4): 151-158. (in Chinese with English abstract)

[4] Lei T W, Zhang Q W, Yan L J, et al. A rational method for estimating erodibility and critical shear stress of an eroding rill[J]. Geoderma, 2008, (3/4): 628-633.

[5] 陈平安，雷孝章. 美国土壤侵蚀模型研究综述[C]//刘国东，梁川，覃光华. 河流开发、保护与水资源可持续利用—第六届中国水水坛水论坛论文集. 北京：中国水利水电出版社，2008：1018-1023.

Chen Pingan, Lei Xiaozhang. A review of soil erosion models in the United States[C]//Liu Guodong, Liang Chuan, Qin Guanghua. River Development and Protection and Sustainable Utilization of Water Resources—The Sixth China Water Forum Proceedings. Beijing: China Water&Power Press, 2008: 1018-1023. (in Chinese with English abstract)

[6] 周正朝，上官周平. 土壤侵蚀模型研究综述[J]. 中国水土保持科学，2004，2(1)：52-56.

Zhou Zhengchao, Shangguan Zhouping. Overview on soil erosion model research[J]. Science of Soil and Water Conservation in China, 2004, 2(1): 52-56. (in Chinese with English abstract)

[7] 张晴雯，雷廷武，潘英华，等. 细沟侵蚀可蚀性参数及土壤临界抗剪应力的有理（实验）求解方法[J]. 中国科学院研究生院学报，2004，21(4)：468-475.

Zhang Qingwen, Lei Tingwu, Pan Yinghua, et al. Rational computational method of soil erodibility and critical shear stress from experimental data[J]. Journal of Graduate School of Chinese Academy of Sciences, 2004, 21(4): 468-475. (in Chinese with English abstract)

[8] van Klaveren R W, McCool D K. Erodibility and critical shear of a previously frozen soil[J]. Transactions of the ASAE, 1998, 41(5): 1315-1321.

[9] 刘宝元，张科利，焦菊英. 土壤可蚀性及其在侵蚀预报中的应用[J]. 自然资源学报，1999，14(4)：345-350.

Liu Baoyuan, Zhang Keli, Jiao Juying. Soil erodibility and its use in soil erosion prediction model[J]. Journal of Natural Resources, 1999, 14(4): 345-350. (in Chinese with English abstract)

[10] Hanson G J, Hunt S L. Lessons learned using laboratory JET method to measure soil erodibility of compacted soils[J]. Applied Engineering in Agriculture, 2007, 23: 305-312.

[11] Singh H V, Thompson A M. Effect of antecedent soil moisture content on soil critical shear stress in agricultural watersheds[J]. Geoderma, 2016, 262: 165-173.

[12] 邢行，陈晓燕，韩珍，等. 饱和与非饱和黄绵土细沟径流水动力学特征及侵蚀阻力对比[J]. 水土保持学报，2018，32(3)：92-97.

Xing Hang, Chen Xiaoyan, Han Zhen, et al. Comparation of hydrodynamic characteristics and flow resistance under rill erosion between saturated and unsaturated loess soil[J]. Journal of Soil and Water Conservation, 2018, 32(3): 92-97. (in Chinese with English abstract)

[13] Nouwakpo S K, Huang C H, Bowling L, et al. Impact of vertical hydraulic gradient on rill erodibility and critical shear stress[J]. Soil Science Society of America Journal2010, 74(6): 1914-1921.

[14] 王彬，郑粉莉，王玉玺，等. 东北典型薄层黑土区土壤可蚀性模型适用性分析[J]. 农业工程学报，2012，28(6)：126-131.

Wang Bin, Zheng Fenli, Wang Yuxi, et al. Adaptability analysis on soil erodibility models in typical thin layer black soil area of Northeast China[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2012, 28(6): 126-131. (in Chinese with English abstract)

[15] Su Z G, Xiong D H, Zhang J H, et al. Variation in the vertical zonality of erodibility and critical shear stress of rill erosion in China’s Hengduan Mountains[J]. Earth Surface Processes and Landforms, 2019, 44(1): 88-97.

[16] Han Z, Chen X Y, Li Y H, et al. Quantifying the rill-detachment process along a saturated soil slope[J]. Soil and Tillage Research, 2020, 204: 104726.

[17] Liu Q J, Wells R R, Dabney S M, et al. Effect of water potential and void ratio on erodibility for agricultural soils[J]. Soil Science Society of America Journal, 2017, 81(3): 622-632.

[18] Bullock M S, Nelson S D, Kemper W D. Soil cohesion as affected by freezing, water content, time and tillage[J]. Soil Science Society of America Journal, 1988, 52(3): 770-776

[19] 董月群，李淑芹，原翠萍，等. 黑麦草对黄土坡面降雨产流产沙过程的影响[J]. 中国农业大学学报，2011，16(4)：67-73.

Dong Yuequn, Li Shuqin, Yuan Cuiping, et al. Impacts of rye grasses on runoff and sedimentation processes from loess slopes[J]. Journal of China Agricultural University, 2011, 16(4): 67-73. (in Chinese with English abstract)

[20] 安娟，郑粉莉，李桂芳，等. 不同近地表土壤水文条件下雨滴打击对黑土坡面养分流失的影响[J]. 生态学报，2011，31(24)：7579-7590.

An Juan, Zheng Fenli, Li Guifang, et al. Effect of raindrop impact on nutrient losses under different near-surface soil hydraulic conditions on black soil slope[J]. Acta Pedologica Sinica, 2011, 31(24): 7579-7590. (in Chinese with English abstract)

[21] Wu B, Wang Z L, Zhang Q W, et al. Evaluation of shear stress and unit stream power to determine the sediment transport capacity of loess materials on different slopes[J]. Journal of Soils and Sediments, 2018, 18: 116-127.

[22] Huang Y H, Li F H, Liu Z Q, et al. Experimental determination of sediment transport capacity of concentrated water flow over saturated soil slope[J]. European Journal of Soil Science, 2020, 72(2): 756-768.

[23] 孙树林，王利丰. 饱和、非饱和有机质粉土抗剪强度的对比[J]. 岩土工程学报，2006，28(11)：1932-1935.

Sun Shulin, Wang Lifeng. Comparison of shear strength between saturated and unsaturated sandy silt[J]. Journal of Geotechnical Engineering, 2006, 28(11): 1932-1935. (in Chinese with English abstract)

[24] 滕延京，盛志强，王曙光. 饱和黏性土抗剪强度的试验方法[J]. 岩土工程学报，2015，37(3)：426-431.

Teng Yanjing, Sheng Zhiqiang, Wang Shuguang. Test method for shear strength of saturated cohesive soil[J]. Journal of Geotechnical Engineering, 2015, 37(3): 426-431. (in Chinese with English abstract)

[25] Saffari P, Noor M J M, Ashaari Y, et al. Shear strength of unsaturated malaysian granitic residual soil[J]. Journal of Testing and Evaluation, 2019, 47(1): 640-653.

[26] 王伟，陈杨，庄晓晖，等. 极端降雨条件下秸秆覆盖坡面水流流速空间分布[J]. 农业工程学报，2022，38(2)：149-156.

Wang Wei, Chen Yang, Zhuang Xiaohui, et al. Spatial distribution of overland flow velocity along straw-mulched slope under extreme rainfall[J]. Journal of Geotechnical Engineering (Transactions of the CSAE),2022, 38(2): 149-156. (in Chinese with English abstract)

[27] 沈海鸥, 郑粉莉, 温磊磊. 细沟发育与形态特征研究进展[J].生态学报，2018，38(19)：6818-6825.

Shen Haiou, Zheng Fenli, Wen Leilei. A research review of rill development and morphological characteristics[J]. Acta ecologica sinica, 2018, 38(19): 6818-6825. (in Chinese with English abstract)

[28] 张科利, 秋吉康宏. 坡面细沟侵蚀发生的临界水力条件研究[J]. 土壤侵蚀与水土保持学报，1998(1)：42-47.

Zhang Keli, Qiuji Kanghong. Critical hydraulic condition of rill erosion onsloping surface[J]. Journal of Soil Erosion and Soil and Water Conservation, 1998(1): 42-47. (in Chinese with English abstract)

[29] Huang Y H, Chen X Y, Li F H, et al. Velocity of water flow along saturated loess slopes under erosion effects[J]. Journal of Hydrology, 2018, 561: 304-311.

[30] Lei T W, Zhang Q W, Zhao J, et al. A laboratory study of sediment transport capacity in the dynamic process of rill erosion[J]. Transactions of the ASAE, 2001, 44(6): 1537-1542.

[31] Lei T W, Zhang Q W, Zhao J, et al. Soil detachment rates for sediment loaded flow in rills[J]. Transactions of the ASAE, 2002, 45(6): 1897-1903.

[32] Huang Y H, Wang W, Lei T W, et al. Saturation effect on the distribution of rill detachment rate[J]. European Journal of Soil Science, 2021, 72(5): 2076-2087.

[33] 黄钰涵. 饱和土壤坡面细沟侵蚀动力机制试验研究[D]. 北京：中国农业大学，2020.

Huang Y H. Experimental Study on the Dynamic Mechanism of Rill Erosion over Saturated Soil Slope[D]. Beijing: China Agricultural University, 2020. (in Chinese with English abstract)

[34] Huang C H, Bradford J M, Laflen J M. Evaluation of the detachmenttransport coupling concept in the wepp rill erosion equation[J]. Soil Science Society of America Journal, 1996, 60(3): 734-739.

[35] Chen X Y, Huang Y H, Zhao Y, et al. Comparison of loess and purple rill erosions measured with volume replacement method[J]. Journal of Hydrology, 2015, 530: 476-483.

[36] 刘纪根，张平仓，陈展鹏. 聚丙烯酰胺对扰动红壤可蚀性及临界剪切力的影响[J]. 农业工程学报，2010，26(7)：45-49.

Liu Jigen, Zhang Pingcang, Chen Zhanpeng. Effects of Polyacrylamide (PAM) on soil erodibility and critical shear stresses for disturbed red soil[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2010, 26(7): 45-49. (in Chinese with English abstract)

[37] Xing H, Huang Y H, Chen X Y, et al. Comparative study of soil erodibility and critical shear stress between loess and purple soils[J]. Journal of Hydrology, 2018, 558: 625-631.

Characteristics of soil erodibility parameter and critical shear stress on saturated loess soil slope

Huang Yuhan1,2, Yang Mengge2, Lei Tingwu1※, Li Fahu1, Wang Wei3

(1.,,100083,;2.,,,530004,;3.,100083,)

Soil erodibility parameter and critical shear stress are important indicators to evaluate the degree of soil erosion sensitivity and the resistance to the shear deformation of water flow. To date, the change of soil erodibility parameter and critical shear stress is unclear in the rill erosion process of saturated loess soil slope. In this study, the maximum rill detachment rates of saturated loess soil slope were determined by a series of soil scouring experiments in the laboratory under different slopes (5°, 10°, 15°, and 20°) and flow rates (2, 4, and 8 L/min). Then, the numerical, modified numerical, and analytical approaches were utilized to calculate the soil erodibility parameters and critical shear stresses. The results showed that the maximum rill detachment rates calculated by the three methods increased with the increase of slope and flow rate over saturated loess soil slope, and the maximum rill detachment rates calculated by the modified numerical method were similar with those calculated by the analytical method. The soil erodibility parameters were 0.470, 0.278, and 0.256 s/m, respectively, and the critical shear stresses were 1.502, 1.306, and 1.367 N/m2, respectively. The modified numerical method improved the calculation accuracy, thus the modified numerical calculation was close to the theoretical value calculated by the analytical method. The soil erodibility parameters of saturated loess soil slope decreased by 16.83%, and the critical shear stresses decreased by 66.97%, compared with those of non-saturated loess soil slope in the same study area. Soil saturation had no significant effect on the soil erodibility parameters, while greatly reducing soil critical shear stress, and then leading to serious soil erosion on loess soil slope. Besides, the critical shear stresses of the saturated loess soil slope were 6.38% larger than those of the saturated purple soil slope, and the soil erodibility parameters of the saturated loess soil slope were 2.26 times those of the saturated purple soil slope. These results indicated that the soil saturation had similar effects on the critical shear stress of the two soils, while the saturated loess soil was more sensitivity on soil erosion than the saturated purple soil. These findings can provide some references to optimize the rill erosion model parameters in different soil slopes under the condition of saturations.

soils; erosion; rills; erodibility parameter; critical shear stress; saturation; maximum rill detachment rate

10.11975/j.issn.1002-6819.2022.17.009

S224.2

A

1002-6819(2022)-17-0083-08

黄钰涵，杨梦格，雷廷武，等. 饱和状态下黄绵土坡面细沟侵蚀可蚀性和临界剪切应力特征[J]. 农业工程学报，2022，38(17)：83-90.doi：10.11975/j.issn.1002-6819.2022.17.009 http://www.tcsae.org

Huang Yuhan, Yang Mengge, Lei Tingwu, et al. Characteristics of soil erodibility parameter and critical shear stress on saturated loess soil slope[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2022, 38(17): 83-90. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2022.17.009 http://www.tcsae.org

2022-05-18

2022-07-10

国家自然科学基金面上项目（41571257）

黄钰涵，博士，讲师，研究方向为土壤侵蚀机理、土壤水文与水土保持。Email：huangyuhan0710@foxmail.com

雷廷武，博士，教授，博士生导师，研究方向为土壤侵蚀机理、土壤水文与水土保持。Email：leitingwu@cau.edu.cn