借助GeoGebra深度剖析一道调研测试题

朱亚军

（江苏省苏州中学，江苏 苏州 215007）

2022届苏州市第2次调研考试结束后，高三师生们对选择题第9题留下了比较深刻的印象.虽然单个小球在竖直平面内的变速圆周运动大家都耳熟能详，但本题设问非常精妙，创新设计，要求考生分析两个小球在同一竖直光滑圆轨道内侧的相对运动问题.有的学生即使蒙对正确答案是（C）选项，其实并没有真正理解其中的道理.有的教师在讲评这道选择题的时候，由于两小球间的相对运动比较抽象、复杂，讲解颇为周折，似乎只可意会，不可言传.为此，笔者尝试借助GeoGebra软件模拟第9题描述的动态情境，进而绘制两个小球运动过程中相关物理量随时间变化的规律，以期给大家今后的教学提供一点帮助.

1 题目及定性分析

例题.如图1所示，竖直平面内固定着内侧光滑的圆形轨道，半径为r.两个质量都为m的小球1、2，某时刻恰好位于轨道的最高点和最低点，初速率分别为，以圆环最低点为重力势能零点，则两小球1、2在运动过程中

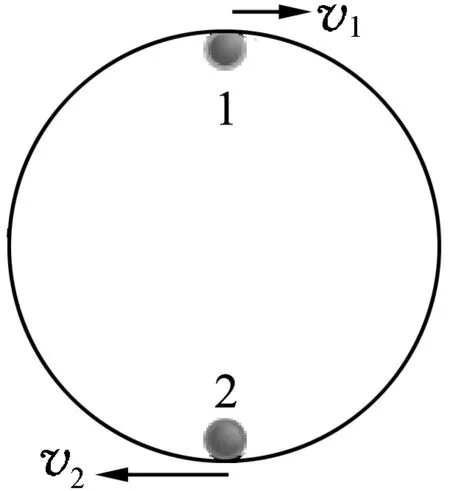
图1

（A）可能会在某一位置中发生碰撞.

（B）可能同时位于水平直径的两端.

（C）两小球距离最近时总动能最小.

（D）系统重力势能的最大值为2mgr.

本题以竖直平面内光滑圆轨道约束两个小球的运动为情境，通过分析小球1、2分别以初速率从最高点、最低点出发顺时针沿圆轨道做变速圆周运动的情况，考查学生对小球在竖直平面内圆周运动速率随时间变化规律的掌握情况，同时考查两球之间的相对运动、系统总动能和总重力势能的变化规律.

根据小球在竖直光滑轨道内维持变速圆周运动的条件和机械能守恒定律可知，题设初速率恰能满足小球1、2分别从最高点、最低点开始沿内侧光滑圆形轨道维持运动的条件，由于，所以，小球1运动到最低点的速率等于v2，小球2运动到最高点的速率等于v1，意味着小球1、2运动的周期相等，不可能会在某一位置中发生碰撞，故选项（A）错误.另外，根据机械能守恒定理可得小球1、2分别运动到水平直径两端时的速率都是所以，小球1、2分别运动到水平直径右端、左端的过程中平均速率不相等，经历的时间必然不同，选项（B）错误.

题干中规定以圆环最低点为重力势能零点，则最初系统的重力势能、动能和机械能分别为2mgr，3mgr和5mgr.在随后的一小段运动过程中，因小球2上升的速率大于小球1下降的速率，故系统的重力势能逐渐增大，直至小球2越过水平直径后与小球1达到同一高度时，系统的重力势能最大，且大于2mgr，系统的总动能最小，小于3mgr.所以，选项（C）正确，选项（D）错误.

2 借助GeoGebra探究小球的运动规律

（1）小球运动的微分方程.

首先，分析小球1的运动情况.如图2所示，从小球1在最高点的时刻开始计时，设t时刻小球运动到图示位置，小球1和圆心O的连线与竖直方向的夹角为θ1，根据牛顿第二定律和圆周运动的规律有

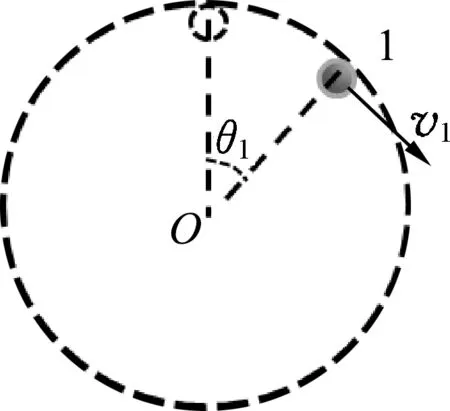
图2

（2）在GeoGebra软件中输入已知量、初始条件和微分方程组.可调节的已知量：轨道半径r＝2.5 m，小球质量m＝0.1 kg；不可调节的已知量：重力加速度g＝9.8 m／s2.

（3）利用“NsolveODE”指令解常微分方程组，绘制小球运动过程中相关物理量随时间变化的图像.

图3所示为θ1- t、ω1- t图像.图4所示为θ2- t、ω2-t图像.

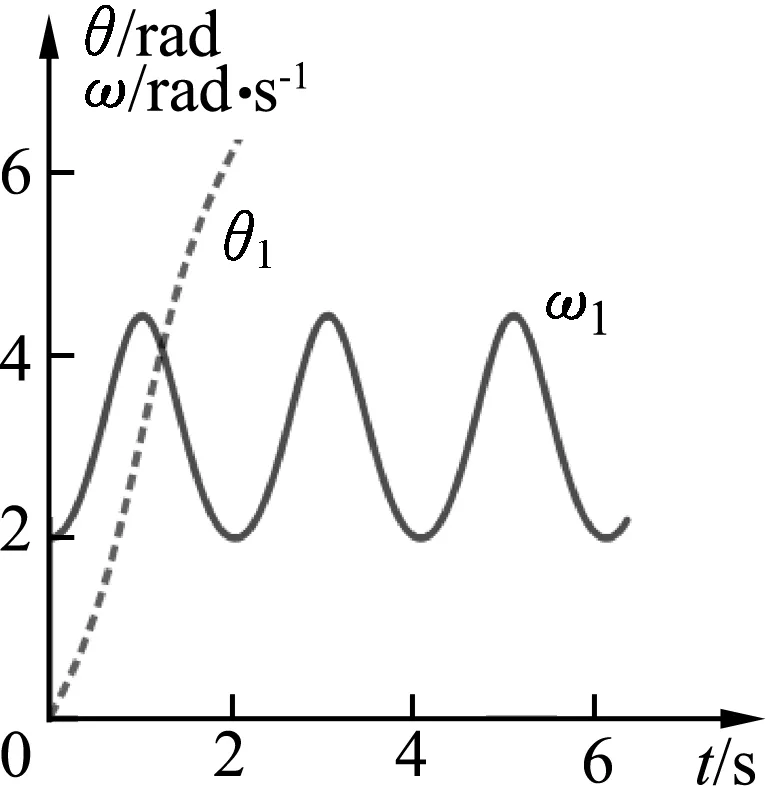
图3

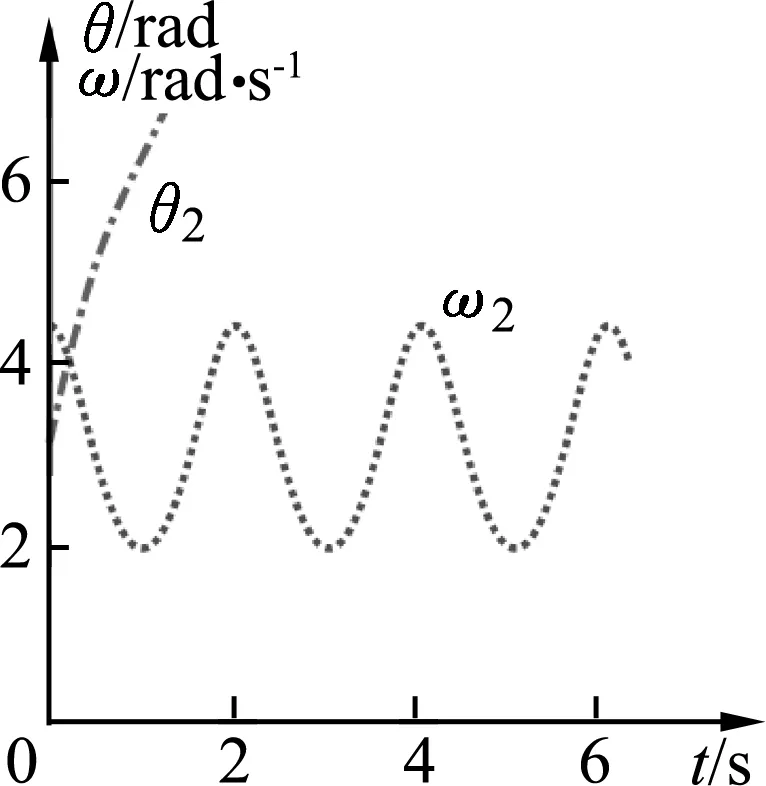
图4

为描绘小球的运动轨迹和运动过程中相关物理量随时间变化的图像，需要从图3、图4中获取任意时刻t对应的θ1、ω1、θ2和ω2的瞬时值.

输入：len＝length（θ1），

描 点：Point（θ1，t），Point（ω1，t），Point（θ2，t），Point（ω2，t），如 图 5所示.

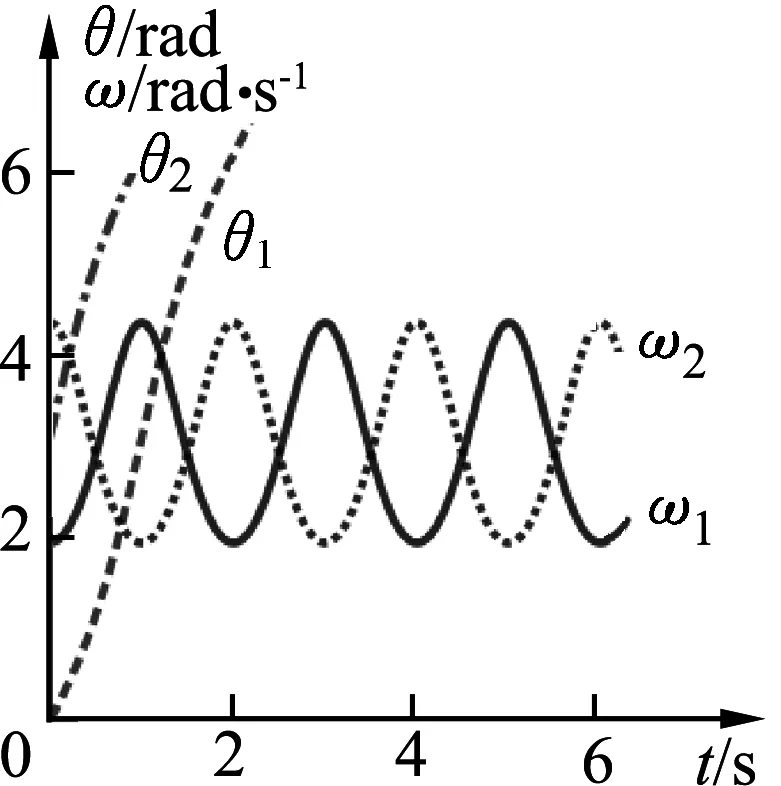
图5

输 入：x1＝r sinθ1，y1＝r（1＋cosθ1）；x2＝－r sinθ2，y2＝r（1－cosθ2）.

输入：（x1，y1）——小球1的位置，Locus（1，t）——小球1的轨迹；（x2，y2）——小球2的位置，Locus（2，t）——小球2的轨迹.小球1、2的初始位置和轨迹如图6所示.

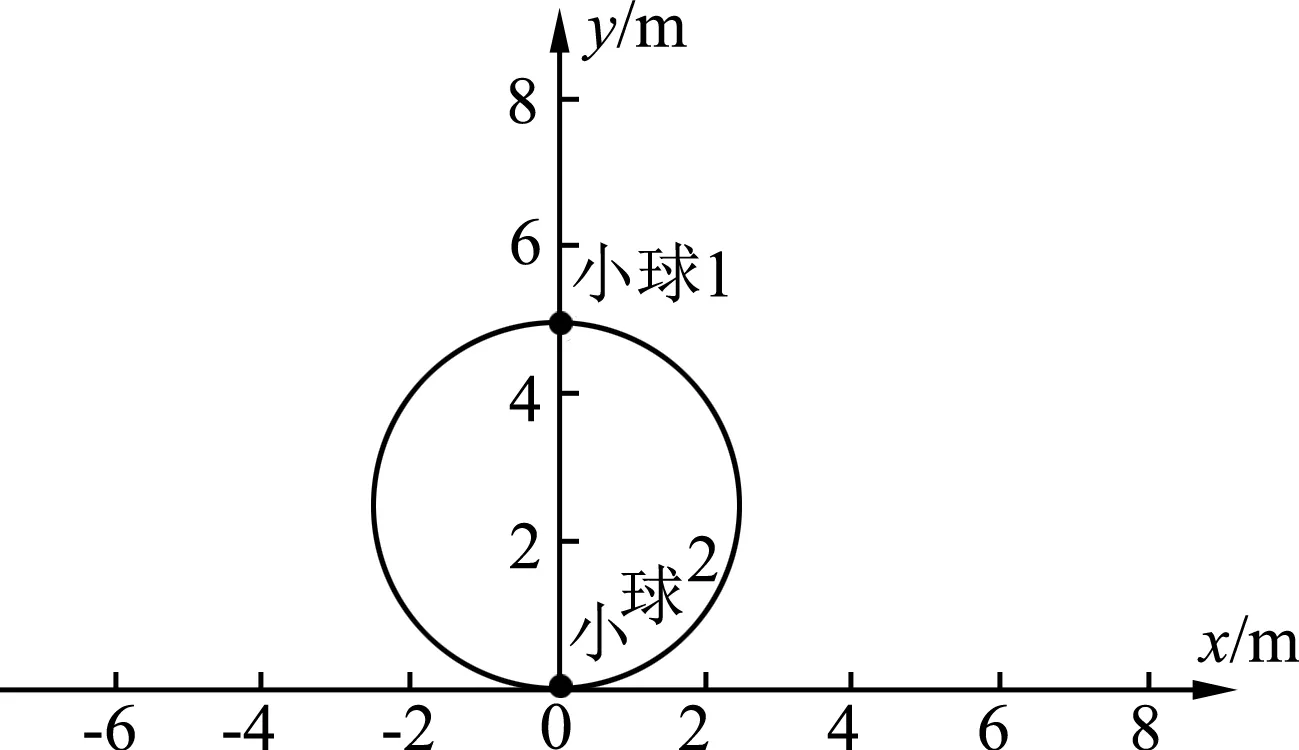
图6

用虚线连接小球1、2，并获取这段虚线的长度l.利用“Locus”指令描绘l- t图像，如图7所示.由此可见，小球1、2之间的最大距离为5.00 m，最小距离约为4.62 m.运动过程中小球1、2不可能发生碰撞.

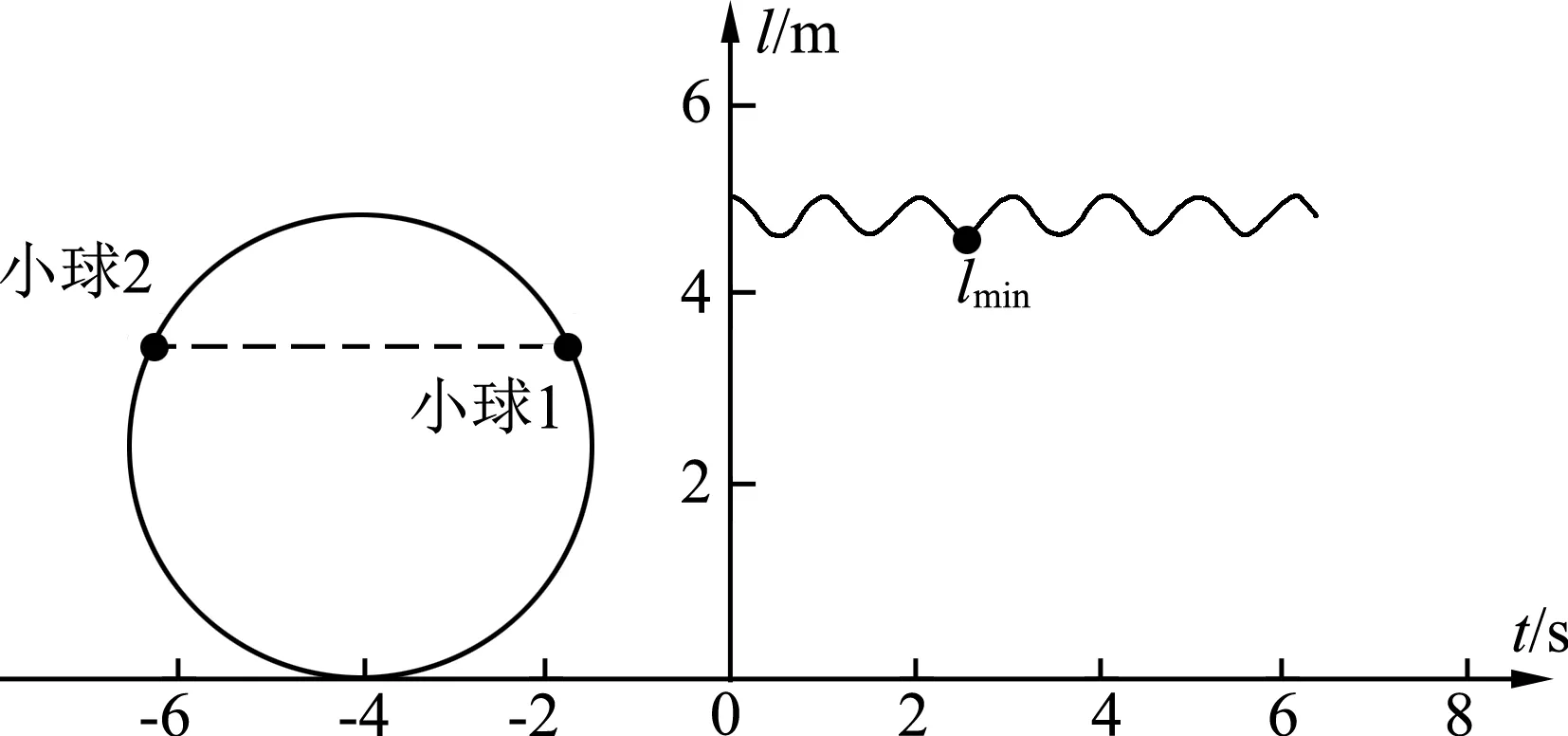
图7

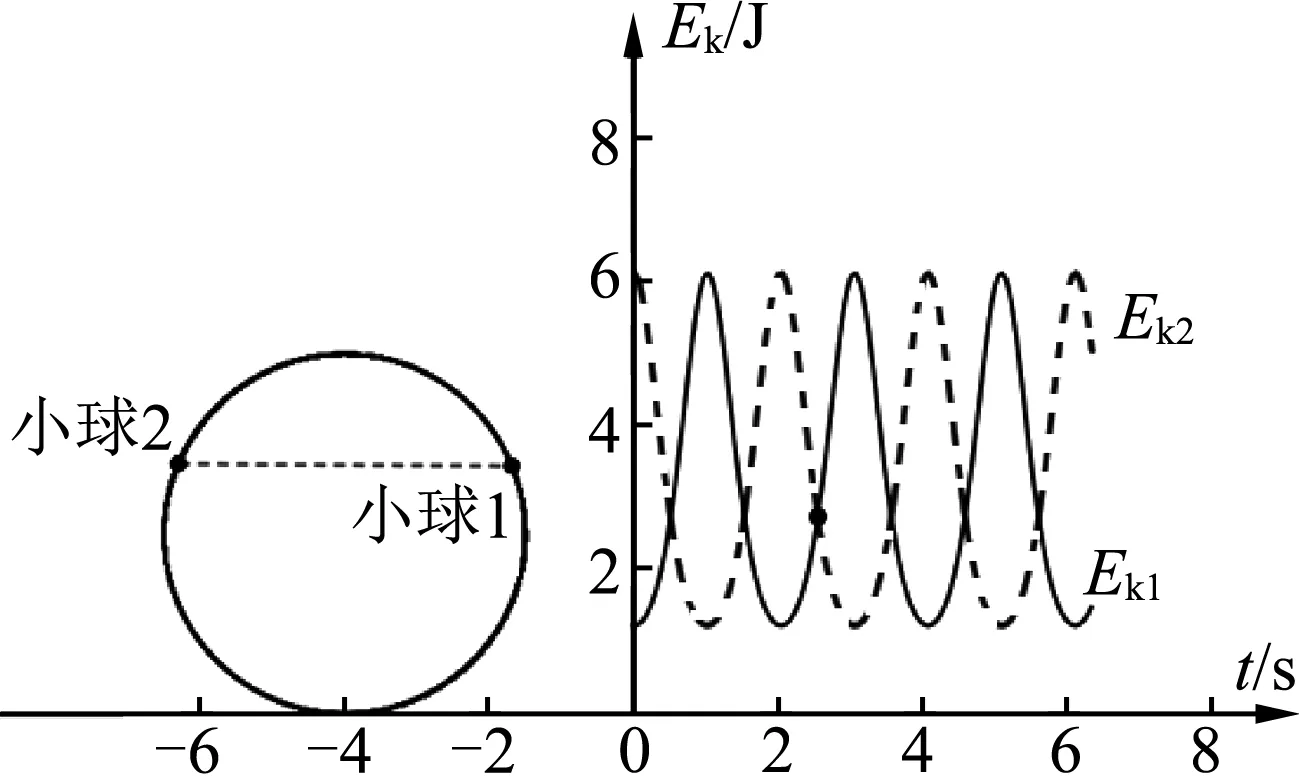
图8

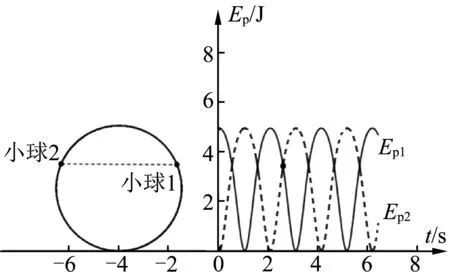
图9

图10

图7—图11表明，当小球1、2的连线水平，且在水平直径的正上方时，两球之间的距离l最小，小球1、2的动能相等，重力势能相等，且重力势能大于动能；两个小球的总动能最小，总重力势能最大，故本题的选项（C）正确.

图11

3 小结

本文借助GeoGebra的“NsolveODE”指令探究小球1、2的运动规律.利用“Locus”指令描绘小球1、2运动过程中相关物理量（θ1，θ2，ω1，ω2，l，Ek1，Ek2，Ep1，Ep2，Ek总和Ep总）随时间t变化的图像，非常直观、形象地呈现小球1、2的相对运动情境和总动能、总重力势能的变化情况.将转瞬即逝的运动过程逐一定格——化动为静，实现竖直平面内光滑圆轨道约束小球运动规律的可视化，突破教学的难点.