基于随机振动法的大跨度双塔斜拉桥地震响应分析
钱 进, 周泽箭
(1.湖南省交通规划勘察设计院有限公司, 湖南 长沙 410200;2.广东省交通规划设计研究院集团股份有限公司, 广东 广州 510507)
0 引言
地震对人类的危害巨大,属于自然灾害[1],具有破坏力大和难以预测的特点,其引发的桥梁破坏常给人民的生命与财产造成巨大损失。因此,对桥梁进行抗震性能分析,确保其在地震作用下的安全和正常使用具有极其重要的意义。而大跨度斜拉桥作为21世纪最具代表性的桥梁之一[2-3],有必要对其抗震性能进行研究。与此同时,我国现行抗震规范细则主要针对跨度不大的桥梁,对于大跨度斜拉桥适用性还不够。所以,大跨度斜拉桥的抗震性能值得深入研究。
在对大跨度斜拉桥地震响应分析中,地震动的空间效应不可忽略[4-5]。空间效应包括:局部场地效应、部分相干效应和行波效应[6]。由于随机振动理论具有概率统计的特点,与实际工程较符合,因此该理论被广泛应用于工程抗震。
本文以某双塔斜拉桥为例,利用ANSYS软件,基于随机振动理论,对某大跨度双塔斜拉桥一致激励下的地震响应进行分析,同时考虑了局部场地效应的影响,为该斜拉桥在地震作用下的动力响应特性提供一定参考。
1 随机振动法概述
随机振动是结合了结构动力学和概率论的基本原理,用以研究随机激励下确定性结构动力响应问题的理论[7]。相较于确定性地震反应分析,随机振动理论基于地震反应谱的功率谱密度与方差对结构展开动力响应分析,其基本原理如下:
对于单自由度体系,根据达朗贝尔原理,其运动微分方程如式(1)所示:
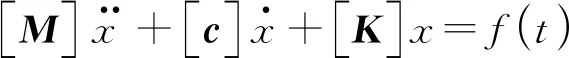
(1)
式中:[K]表示刚度矩阵;[M]表示质量矩阵;[c]表示阻尼矩阵;f(t)为随机变量。
由于输入的f(t)为随机变量,所以输出x(t)也为随机变量,运用统计学方法,根据Duhamel积分公式[8]对式(1)求解,得:
(2)
两边同时取均值后如式(3)所示:
(3)
即可得:
(4)
采用相同的方法,随机变量的自相关函数可表示为:
(5)
将式(3)、式(4)代入式(5)可得:
Rx(τ)=[RF(τ)·h(τ)]h(-τ)
(6)
将式(6)的相关函数进行傅里叶变换,可得:
Sx(ω)=|H(ω)|2SF(ω)
(7)
式中:Sx(ω)为输出的自反应谱密度函数;SF(ω)为输入的自反应谱密度函数;H(ω)为频率响应函数。
2 有限元模型建立与动力特性分析
2.1 工程概况
本文案例为某大跨度双塔斜拉桥(见图1),桥跨布置为(145+350+145)m,桥面宽28 m,塔高125.8 m。主塔每侧各设14对斜拉索,全桥共112根斜拉索。主梁和桥塔均采用钢筋混凝土结构,混凝土强度等级为C50。主梁采用预应力混凝土箱梁结构,斜拉索采用扇形方式布置。
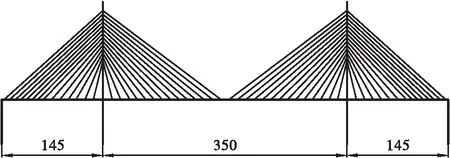
图1 某大跨双塔斜拉桥示意(单位: m)
2.2 有限元模型的建立
运用ANSYS建立有限元模型。其中,主梁、主塔分别采用BEAM4梁单元和BEAM188梁单元模拟;钢臂采用MPC184S模拟;斜拉索采用LINK10单元模拟,单元属性为受拉。有限元模型如图2所示。

图2 双塔斜拉桥有限元模型示意
2.3 动力特性分析
结构动力特性是结构的固有属性,包括周期、振型等,它们只与结构的质量、刚度和材料等有关。结构的动力特性决定了结构的动力响应特性,是结构动力计算和分析的基础。斜拉桥结构形式复杂、斜拉索质量轻和阻尼较小的特点使得其动力特性成为人们在实际工程中所重视的问题。因此,对斜拉桥的动力特性进行分析是有必要的。本案例桥梁结构的自振特性如表1所示。
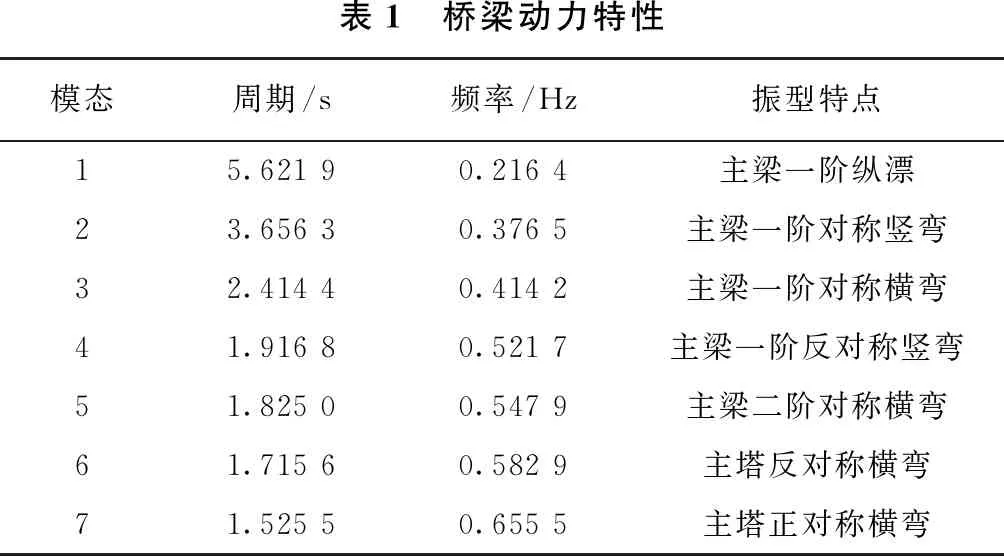
表1 桥梁动力特性模态周期/s频率/Hz振型特点15.621 90.216 4主梁一阶纵漂23.656 30.376 5主梁一阶对称竖弯32.414 40.414 2主梁一阶对称横弯41.916 80.521 7主梁一阶反对称竖弯51.825 00.547 9主梁二阶对称横弯61.715 60.582 9主塔反对称横弯71.525 50.655 5主塔正对称横弯
从表1可以得出本文所采用的双塔斜拉桥的动力特性为: ①自振周期较长。本模型一阶振动为主梁纵漂,周期较长,达到了5.621 9 s,频率为0.216 4 Hz,体现了斜拉桥属于柔性结构的特点。②自振频率非常密集。但该桥的自振频率是缓慢均匀增加的,表明了该斜拉桥结构动力特性复杂。
3 地震响应分析
3.1 随机振动模型选取及参数确定
主要采用随机振动理论中的平稳随机激励模型。在分析桥梁随机地震响应中,地震动的强度等特征一般采用功率谱密度函数来表示。该双塔斜拉桥随机地震响应分析的地震动模型选用杜修力[9]随机振动模型,其模型表达式如式(8)所示:
(8)
式中:ωg为土层的频率;ω0为低频拐角频率;ζg为土层阻尼比;S0为白谱强度;Tg为平稳持时;D为震源辐射加速度脉冲宽度。
模型的场地类别为一类,抗震烈度为8度,地震烈度为7度。具体参数取值参考杜修力模型设计地震动功率谱参数:ωg=26.08,ω0=1.41,ζg=0.85,S0=32.69,Tg=15.84,D=0.009。当考虑三维地震联合作用时,纵向、横向和竖向的加速度输入比值为1∶0.85∶0.65[10]。
局部场地效应采用屈铁军等[11]提出的线性回归拟合公式,如式(9)所示:
ΔS0=0.257 1 Δh-0.012 4Δx
(9)
式中: ΔS0表示自功率差值,cm2/s3;Δh为土层覆盖厚度差值,m;Δx为震中距差,m。
3.2 一致激励下随机地震响应分析
计算分析了一致激励下4种不同工况对结构的地震响应,一致激励是指各支撑点位置输入的地震动相同,三维激励主要考虑了结构在纵向、横向和竖向3个方向同时输入地震动。一致激励下的4种工况如表2所示。

表2 一致激励下的工况工况激励类型1横向激励2纵向激励3竖向激励4横向+纵向+竖向激励
按照选定的工况,利用杜修力随机振动模型作为地震激励输入,计算结构的地震响应,关键截面位移响应和典型截面内力计算结果如图3~5所示。图4中,由于在工况3和工况4作用下,主梁横向弯矩较小,故未在图中表示。
计算结果表明: ① 主梁的竖向位移主要因竖向激励产生,且纵向激励对主梁竖向位移也有一定影响,但横向激励对其影响不明显;三维激励时主梁竖向位移大于竖向激励下的竖向位移;② 主梁的横向弯矩主要因横向激励产生,且在主梁跨中出现最大值,纵向激励和竖向激励作用下几乎不产生横向弯矩,在抗震设计时应重视主梁跨中处的横向抗震要求;③ 主塔横桥向弯矩主要由纵向激励引起,三维激励下主塔横桥向弯矩比纵向激励下横桥向弯矩稍大。④ 综合分析各工况激励下结构的地震响应结果,发现三维激励下结构的地震响应一般较一维输入稍大,同时三维激励下结构的响应更加全面,为使结构更好地满足抗震要求,应着重考虑三维激励下结构的地震响应。
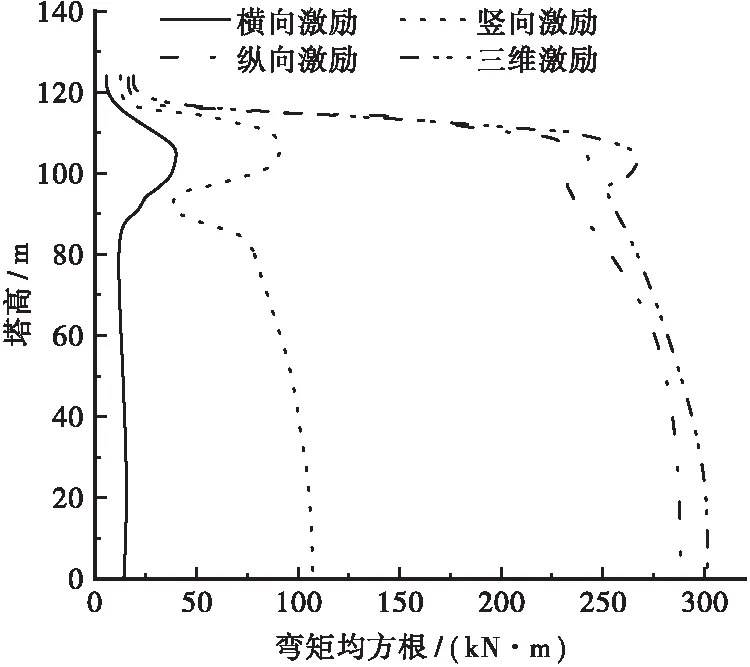
图3 主梁竖向位移均方根
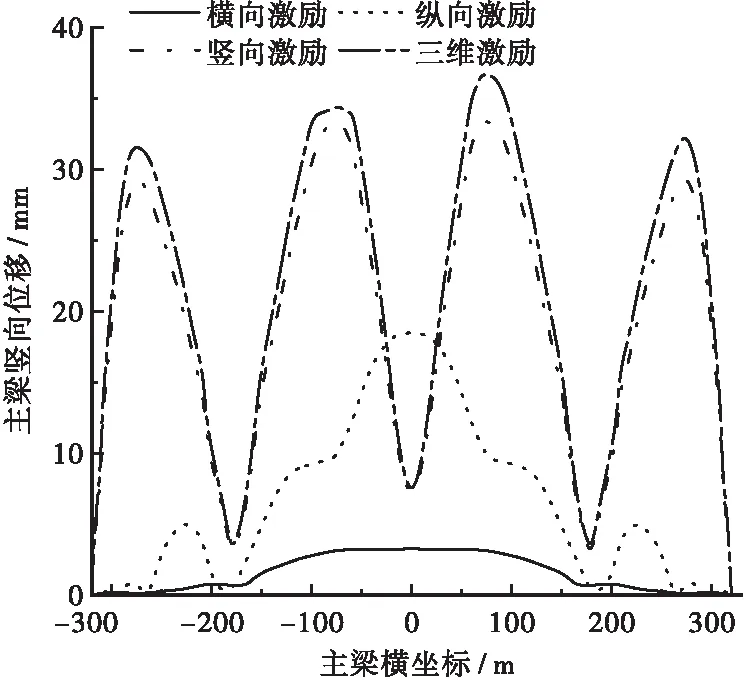
图4 主梁横向弯矩均方根
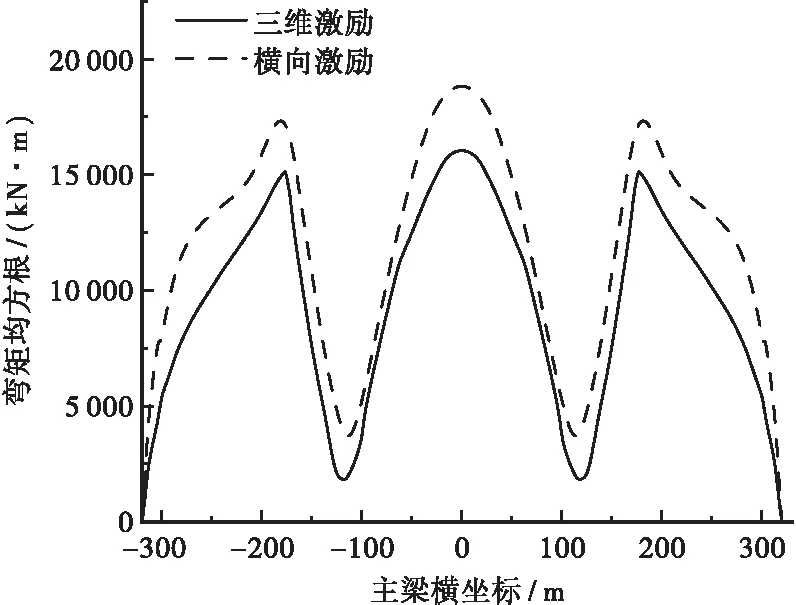
图5 主塔横桥向弯矩均方根
3.3 局部场地效应影响分析
局部场地效应按式(6)分析,此处按Δh=5m、Δx=495 m,考虑南北主塔支撑处的场地差异,并且假设各支撑点间完全相干,结果如图6~8所示。
分析图6~8可知,对比一致激励下的随机地震响应,考虑局部场地效应后,该桥地震响应变化较大,且均呈增大趋势。分析图5可以发现,局部场地效应使主梁位移显著增大,增幅达到了26%;分析图7可知,局部场地效应会使弯矩在波峰处显著增大,但主梁的其它位置变化不大;另外,局部场地效应使顺桥向弯矩增大了30%。因此,对于大跨度斜拉桥,应充分考虑局部场地效应对结构随机地震响应的影响。
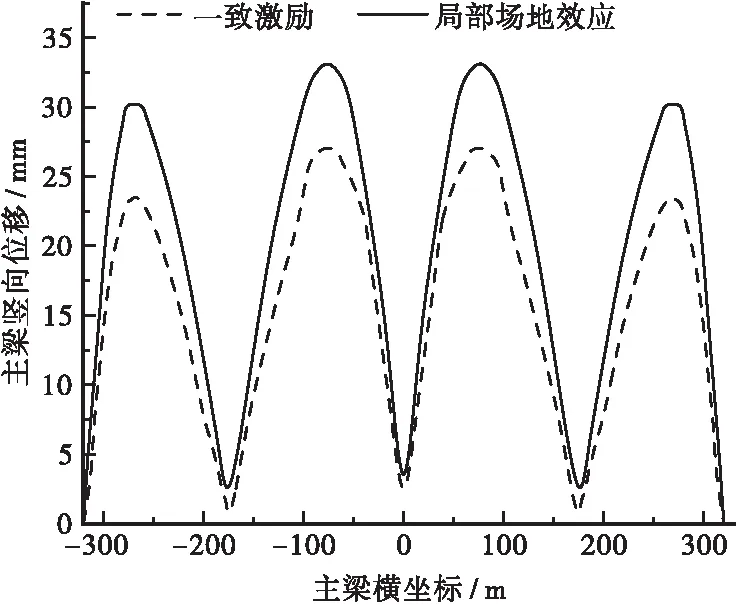
图6 主梁竖向位移均方根
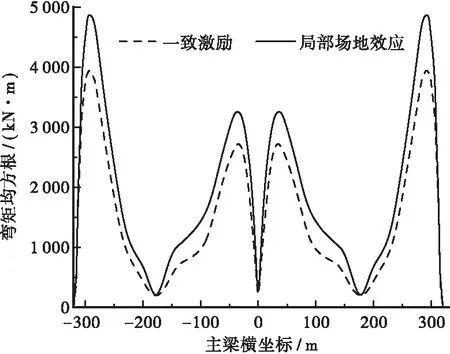
图7 主梁横向弯矩均方根
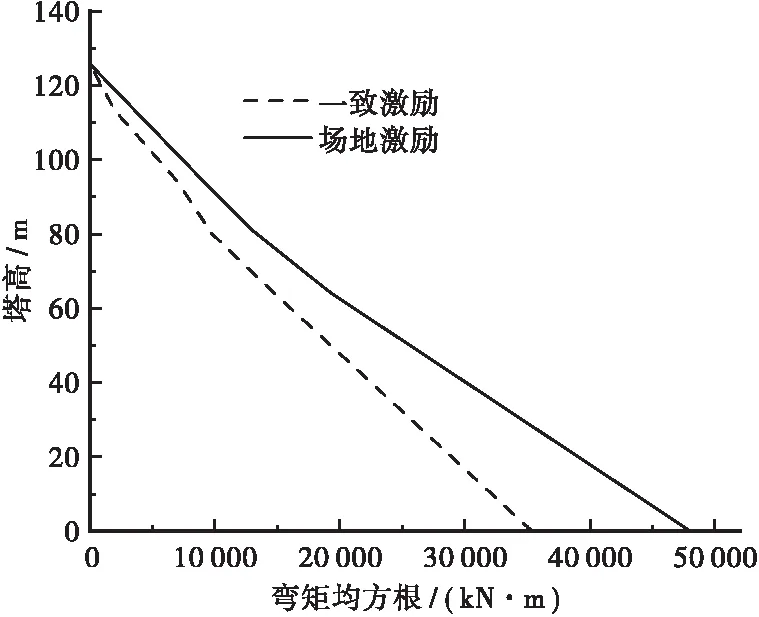
图8 主塔顺桥向弯矩均方根
4 结论
以某大跨度双塔斜拉桥工程为实例,基于随机振动法,分析了4种不同工况在一致激励下的随机地震响应,同时分析了局部场地效应对其影响,得到结论如下:
1) 一致激励下,单维地震输入均会产生某一响应的峰值。比较分析三维地震输入和单维地震输入的地震响应,发现三维激励下结构的地震响应一般较一维输入稍大,同时三维激励下结构的响应更加全面,为使结构更好地满足抗震要求,应着重考虑三维激励下结构的地震响应。
2) 对比在一致激励下的随机地震响应,考虑局部场地效应后,结构地震响应变化较大,且均呈增大趋势,其中主梁位移均方差和主塔顺桥向弯矩均方根增幅分别达到了26%和30%。因此,局部场地效应对大跨度斜拉桥随机地震响应的影响巨大,设计时应予以考虑。

