哑铃型截面钢管混凝土拱桥动力特性和稳定性研究

吴 灿， 相斌辉， 陈 坤， 习明星 ，张 鸿

(1.南昌工程学院 土木与建筑工程学院， 江西 南昌 330099； 2.江西交通咨询有限公司， 江西 南昌 330008)

0 引言

桥梁结构的自振特性研究对桥跨结构的抗震设计、抗风稳定性分析、健康检测和维护等都有着重要的意义，桥梁的自振特性包括桥梁的自振频率与主振型，是进行结构动力分析和抗震设计的重要参数，也是使用阶段判别桥梁是否存在损伤的基本依据[1-4]。而在大跨度钢管混凝土拱桥中， 拱肋作为主要承重构件对拱桥稳定性能与动力性能影响最为显著，因此对拱肋主要横向联系的横撑研究也很有必要[5]。国内一些科研工作者在这方面做了些研究，王頠、董晓康等[6-7]采用有限元分析软件，对钢管混凝土拱桥的动力特性进行了研究，分析了主拱圈含钢率、横撑截面积及布置形式等结构参数对拱桥结构动力特性的影响。朱亚飞等[8]采用有限元方法建立了习营下承式钢管混凝土拱桥三维计算模型，求解了桥梁的自振频率和振型，结合桥面振动实测频率验证了桥梁模型的准确性。孙昊、成凯等[9-10]运用有限元方法对钢管混凝土人行拱桥进行了动力特性研究，分析了拱肋刚度和横撑数量对该类型桥梁自振特性的影响。 另外，还有一些文献对钢管混凝土提篮拱桥的动力特性和稳定性进行研究[11-12]。

上述研究主要针对桁式截面或单圆管截面钢管混凝土拱桥，而关于大跨径哑铃型截面钢管混凝土拱桥的动力特性研究方面的文献比较少见。为此，本文以木高金沙江大桥为工程背景，采用有限元方法对哑铃型截面钢管混凝土拱桥的动力特性进行研究，并分析了矢跨比、横撑布置形式等结构参数对该桥结构动力特性和稳定性的影响规律，丰富了钢管混凝土拱桥动力特性的研究内容，可为同类型桥梁的设计和施工提供借鉴参考。

1 计算理论

1.1 结构自振频率和振型

如果结构受到外部因素的干扰发生振动，在以后的振动过程中不再受到外部干扰作用，这种振动称为自由振动；若在振动过程中还不断受到外部激振力的作用，则称为强迫振动。然而，结构在强迫振动时各截面的最大内力和位移都与结构自由振动的频率和振动形式密切相关，因而寻求自振频率和振型就成了研究结构动力特性的前提[13-14]。无阻尼多自由度体系自由振动运动方程为:

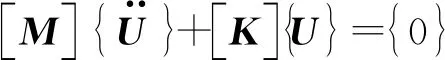
(1)

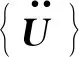
式(1)是一个二阶线性齐次常微分方程租，假设结构振动为简谐振动，则方程的解可写成U(t)=φsin(ωt+φ)，这里，φ是位移幅值向量或者振型，代入式(1)，消去公因子sin(ωt+φ)，得:

(K-ω2M)φ=0

(2)

式：(2)是位移幅值φ的齐次方程，也称为振型方程。为了得到φ的非零解，应使系数行列式为零，即:

D=|K-ω2M|=0

(3)

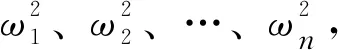
1.2 拱桥稳定性分析理论

实际结构因不可避免的构件初弯曲、荷载初偏心、截面形和材料性质方面的缺陷等不完美因素，丧失稳定性，所以工程上的失稳问题严格来说都属于第二类失稳；由于第一类失稳的临界荷载是第二类失稳临界荷载的上限值，又第一类失稳问题数学方程式清晰明了，求解简单，故通常可以通过求解第一类失稳的临界荷载，将其乘以一定的折减系数以得到相应的临界荷载[16]。结构静力计算方程为：

([KD]+[KG]){δ}={F}

(4)

式中：[KD]是结构的弹性刚度矩阵；[KG]是结构的几何刚度矩阵；{δ}为位移列向量；{F}为节点荷载。

当荷载不断增加，则结构位移不断增大，由于[KG]与荷载大小有关，这时结构的力与位移不再是线性关系，假如{F}增加到λ{F}时，结构出现随遇平衡状态，此时就是要求的临界荷载。此时的结构方程可表示为：

([KD]+λ[KG]){δ}=λ{F}

(5)

若λ足够大，使结构达到随遇平衡状态，当{δ}变为{δ}+{Δλ}时，式(5)也能满足，即：

([KD]+λ[KG])({δ}+{Δλ})=λ{F}

(6)

同时满足式(5)和式(6)的条件是：

([KD]+λ[KG]){δ}=0

(7)

式(7)就是计算结构稳定的特征方程，若方程有n阶，则理论上存在n个特征值λ1、λ2…λn和对应的n个特征向量(失稳模态)。但在工程上只有最小的特征值或稳定安全系数才有实际意义。

2 工程概况及计算模型建立

2.1 工程概况

木高金沙江大桥位于香格里拉市上江乡木高村北侧，上跨金沙江，桥头设置引道与金江公路连接，北岸连接S226省道。木高金沙江大桥为预应力混凝土系杆拱桥，计算跨径L=120m，拱轴线为二次抛物线，矢跨比1/5，矢高为24 m。拱肋采用哑铃型钢管混凝土，每个钢管外径1.0 m，钢管及腹板壁厚0.014 m，内充C50微膨胀混凝土。系杆采用箱型截面，系杆高为1.8m，宽为1.4 m，壁厚0.3 m；拱桥吊杆间距为5.4 m，每片拱肋设吊杆21根；端横梁采用箱型断面，高1.50～1.585 m，宽1.90 m。拱桥横撑采用双管桁架型一字横撑，由外径0.7 m和0.3 m钢管焊接而成，共5组，分别位于5#、8#、11#、14#、17#吊杆处。木高金沙江大桥主跨布置见图1，拱肋风撑见图2。

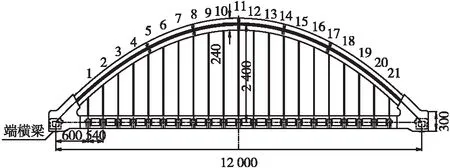
(a) 主跨布置

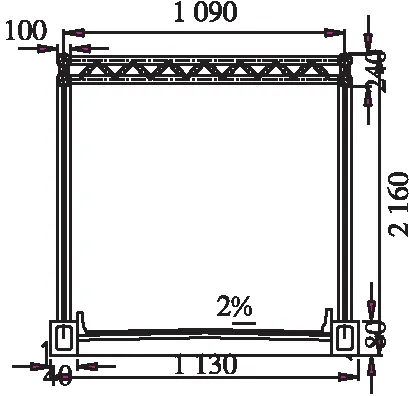
(b) 横断面

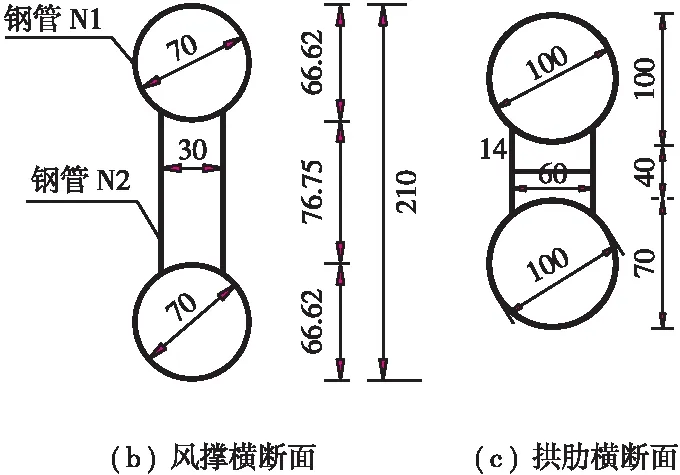
图2 木高金沙江大桥拱肋风撑示意(单位： cm)

2.2 计算模型建立

本文采用桥梁大型通用软件Midas Civil对木高金沙江大桥进行建模，上部结构共有724个节点，790个单元，其中拱肋、横系梁、横撑均采用梁单元模拟，吊杆采用桁架单元模拟，梁单元共有748个，桁架单元共有42个。由于本文主要计算成桥状态桥梁的整体稳定性与动力特性，故支座都采用固结，限制所有平动与转动自由度。桥面板及二期荷载以等效均布荷载形式加载在横梁上，钢管和管内混凝土组合在一起，等效处理成单一弹性模量和密度的梁单元，按抗弯刚度等效的原则计算组合截面的等效弹性模量，按抗拉刚度等效的原则计算组合截面的等效截面面积[17]，即:

EI=ESIS+ECIC

(8)

EA=ESAS+ECAC

(9)

式中：ES、IS、AS分别为钢管部分的弹性模量、惯性矩和截面面积；EC、IC、AC分别为与混凝土对应的弹性模量、惯性矩和截面面积；A是组合截面的折算弹性模量和截面总惯性矩。

木高金沙江大桥三维空间计算模型见图3。

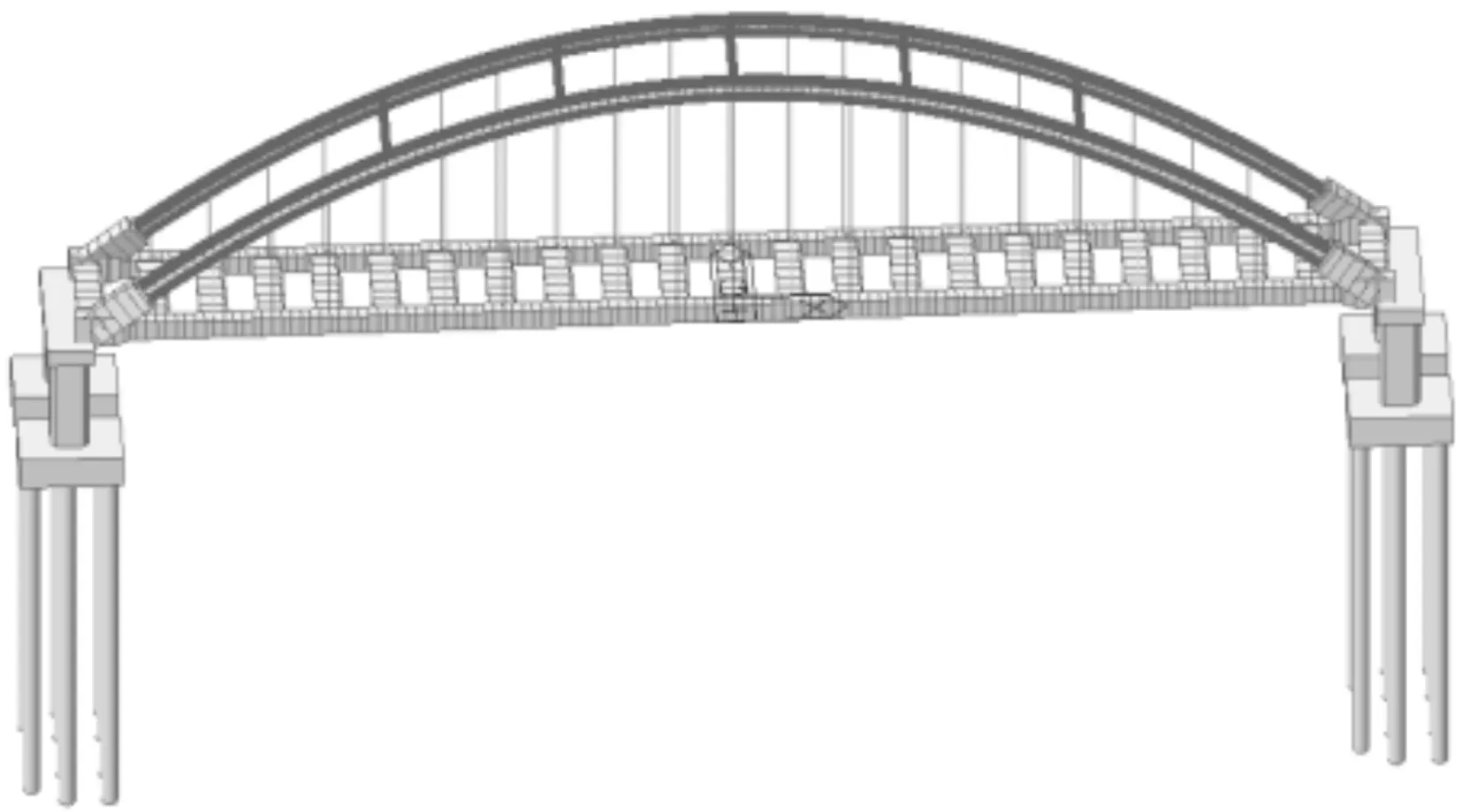
图3 全桥有限元计算模型

3 计算结果分析与讨论

3.1 横撑布置形式对拱桥动力特性影响分析

为了研究横撑布置形式对木高金沙江大桥动力性能的影响，本文拟定了5种不同的横撑布置工况，分别计算木高金沙江大桥的自振频率和振型。各工况具体布置内容如下：工况1为原设计布置的横撑，即5#、8#、11#、14#、17#吊杆处各布设一字横撑；工况2在原设计的基础上，将拱顶处的一字横撑改为“K”撑，其余横撑布置不变；工况3在原设计的基础上，将拱顶处的一字横撑改为“米”撑，其余横撑布置不变；工况4在拱脚处将一字横撑改为“K”撑，其余横撑布置不变；工况5在临近拱脚处将一字横撑改为“米”撑，其余横撑布置不变。各工况拱桥的自振频率计算结果及振型特点分别如表1和表2所示，图4为各工况拱桥的自振频率变化趋势曲线。

通过上述计算结果分析可知：

1)桥梁的振动形式大致分为拱肋面外正对称、反对称振动，拱肋与桥面系竖向竖弯振动和桥梁整体扭转振动等3种。

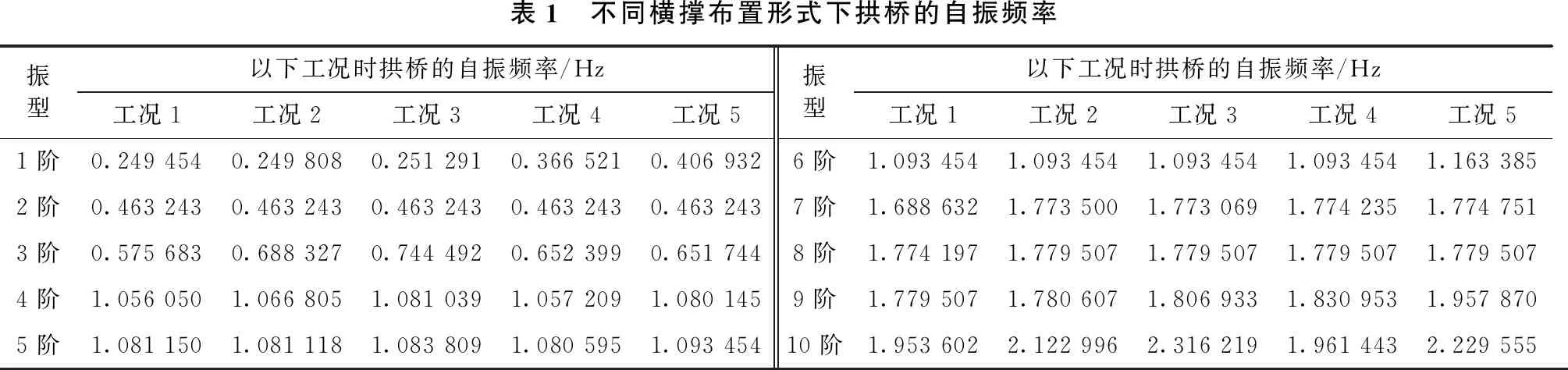
表1 不同横撑布置形式下拱桥的自振频率振型以下工况时拱桥的自振频率/Hz工况1工况2工况3工况4工况5振型以下工况时拱桥的自振频率/Hz工况1工况2工况3工况4工况51阶0.249 4540.249 8080.251 2910.366 5210.406 9322阶0.463 2430.463 2430.463 2430.463 2430.463 2433阶0.575 6830.688 3270.744 4920.652 3990.651 7444阶1.056 0501.066 8051.081 0391.057 2091.080 1455阶1.081 1501.081 1181.083 8091.080 5951.093 4546阶1.093 4541.093 4541.093 4541.093 4541.163 3857阶1.688 6321.773 5001.773 0691.774 2351.774 7518阶1.774 1971.779 5071.779 5071.779 5071.779 5079阶1.779 5071.780 6071.806 9331.830 9531.957 87010阶1.953 6022.122 9962.316 2191.961 4432.229 555

表2 不同横撑布置形式下拱桥的振型特征振型振型特征工况1工况2工况3工况4工况51阶拱肋1阶正对称侧弯拱肋1阶正对称侧弯拱肋1阶正对称侧弯拱肋1阶正对称侧弯拱肋1阶正对称侧弯2阶拱肋1阶正对称侧弯拱肋1阶正对称侧弯拱肋1阶正对称侧弯拱肋1阶正对称侧弯拱肋1阶正对称侧弯3阶拱肋面外1阶反对称侧弯拱肋1阶反对称侧弯拱肋1阶反对称侧弯拱肋1阶反对称侧弯拱肋1阶反对称侧弯4阶拱肋2阶正对称侧弯拱肋2阶正对称侧弯拱肋、桥面系面内1阶反对称竖弯拱肋2阶正对称侧弯拱肋、桥面系面内1阶反对称竖弯5阶拱肋、桥面系面内1阶反对称竖弯拱肋、桥面系面内1阶反对称竖弯拱肋1阶面外反对称侧弯,桥面系1阶反对称竖弯拱肋、桥面系面内1阶反对称竖弯拱肋1阶面外反对称侧弯,桥面系1阶反对称竖弯6阶拱肋1阶面外反对称侧弯,桥面系1阶反对称竖弯拱肋1阶面外反对称侧弯,桥面系1阶反对称竖弯拱肋2阶正对称侧弯拱肋1阶面外反对称侧弯,桥面系1阶反对称竖弯拱肋2阶正对称侧弯7阶拱肋面外2阶反对称侧弯拱肋、桥面系面内1阶正对称竖弯拱肋、桥面系面内1阶正对称竖弯拱肋、桥面系面内1阶正对称竖弯拱肋、桥面系面内1阶正对称竖弯8阶拱肋、桥面系面内1阶正对称竖弯拱肋2阶面外正对称侧弯,桥面系2阶正对称竖弯拱肋2阶面外正对称侧弯,桥面系2阶正对称竖弯拱肋2阶面外正对称侧弯,桥面系2阶正对称竖弯拱肋2阶面外正对称侧弯,桥面系2阶正对称竖弯9阶拱肋2阶面外正对称侧弯,桥面系2阶正对称竖弯全桥扭转全桥扭转拱肋面外2阶反对称侧弯全桥扭转10阶全桥扭转全桥扭转全桥扭转全桥扭转拱肋面外2阶反对称侧弯

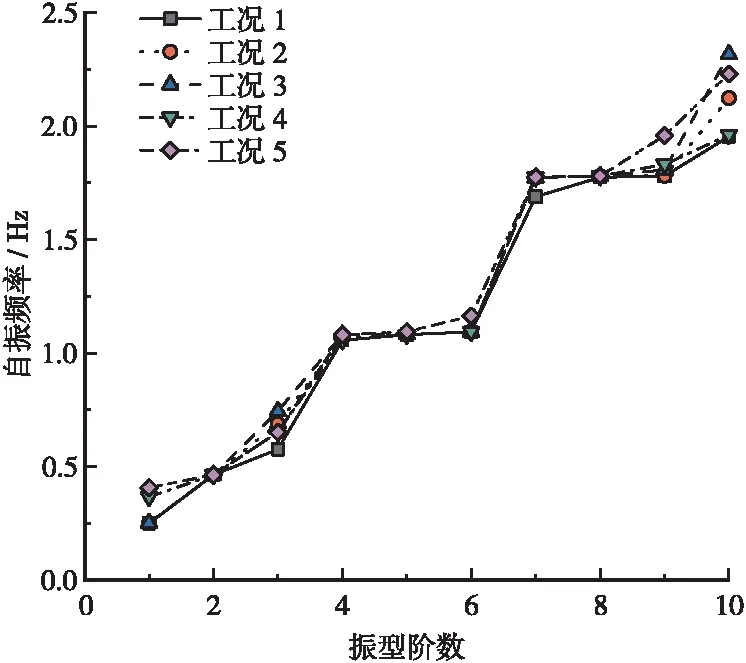
图4 不同横撑布置形式与拱桥自振频率变化曲线

2)5种工况下，振动形式都是低阶发生面外振动，中阶发生面内竖弯振动，高阶发生桥梁整体扭转振动，改变横撑形式基本不会改变桥梁的振动形式。此外，从低阶到高阶的不同振动形式可以看出，木高金沙江大桥的整体面外刚度小于面内刚度，小于抗扭刚度。

3)改变临近拱脚处的横撑布置形式，相应的低阶频率变化较大，前3阶都为面外振动，说明临近拱脚处的横撑布置形式对钢管混凝土拱桥面外基频影响较大，对面内基频影响不大；同时发现，拱顶处的横撑布置形式对面外振动频率与面内竖弯振动频率影响不大，而对扭转振动影响较大，这说明结构形式对拱桥的抗扭刚度影响较大。

4)到了第9阶甚至第10阶才出现全桥扭转的振型，说明木高金沙江的桥面系与拱肋的整体扭转刚度较大，这主要是由于横梁的布设合理，使得横梁与系杆组成的框架体系刚度较大，不易发生扭转振动。

3.2 横撑布置形式对拱桥稳定性影响分析

肋拱桥不同于板拱桥，其横向联系非常弱，而在空间结构环境中，肋拱极易发生面外失稳，因此肋拱之间的横撑就起到了非常重要的作用。为了研究不同横撑的布置形式对木高金沙江稳定性能的影响，现以前文所述的5种工况对拱桥的稳定性进行计算，不同横撑布置形式下的拱桥稳定安全系数如表3所示。

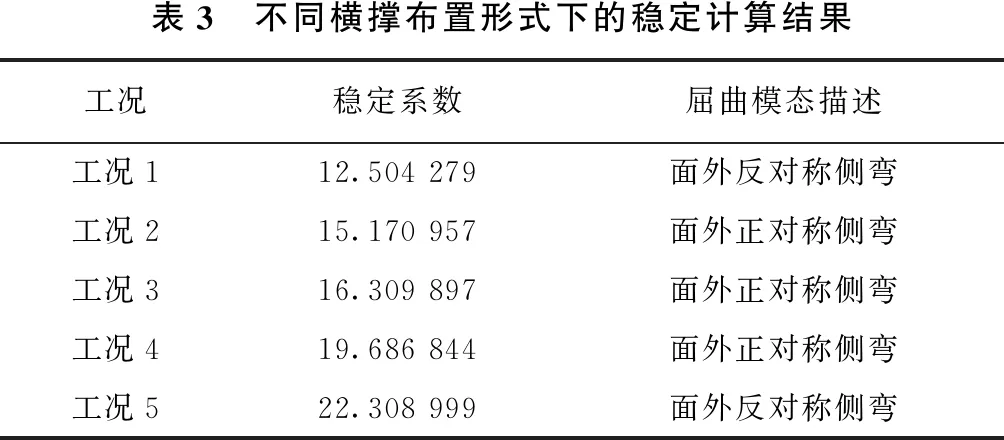
表3 不同横撑布置形式下的稳定计算结果工况稳定系数屈曲模态描述工况112.504 279面外反对称侧弯工况215.170 957面外正对称侧弯工况316.309 897面外正对称侧弯工况419.686 844面外正对称侧弯工况522.308 999面外反对称侧弯

从表3可以看出，5种工况下木高金沙江大桥的稳定安全系数都远大于4，符合规范要求，这主要是因为该桥的桥跨径相对较小，原设计布设5道一撑(工况1)即可提供足够的整体刚度，使其满足稳定性要求。从表3计算结果对比发现，改变横撑的形式，对于提升拱桥的整体稳定安全系数有显著影响。例如，工况4和工况5的拱桥稳定系数分别比工况1增加了57%和78%，由此可以看出“米”撑好于“K”撑，“K”撑好于一撑。

从不同横撑布置形式下5种工况拱桥的屈曲模态可以看出(由于篇幅有限未示出)，各工况下前3阶均为面外失稳，第4阶才出现面内失稳，说明钢管混凝土拱桥的面外失稳是桥梁的主要问题，在设计施工中应重点考虑此类桥型的面外失稳。此外，拱肋在1/4跨径处和跨中处相对错动变形较大，说明这两处是钢管混凝土拱桥容易发生面外失稳的地方，这符合一般拱桥的失稳规律，因此，应增强木高金沙江大桥拱肋1/4跨径处和跨中处的横向联系。

3.3 矢跨比对拱桥动力特性影响分析

拱桥矢跨比是影响拱桥弯矩和压力的重要因素，因此矢跨比对拱桥的动力特性和稳定性能有重要影响。为了研究矢跨比对木高金沙江大桥动力性能和稳定性的影响，本节采用了5种工况进行分析，以木高金沙江大桥的跨径不变(跨径120 m)，改变矢高，从而改变桥梁的矢跨比，拱肋的横撑采用原设计布置形式。工况1的矢跨比为0.05(矢高6 m)，工况2的矢跨比为0.1(矢高12 m)，工况3的矢跨比为0.2(矢高24 m)，工况4的矢跨比为0.3(矢高36 m)，工况5的矢跨比为0.4(矢高48 m)。5种工况木高金沙江大桥的自振频率计算结果如表4所示，各工况振型描述如表5所示。

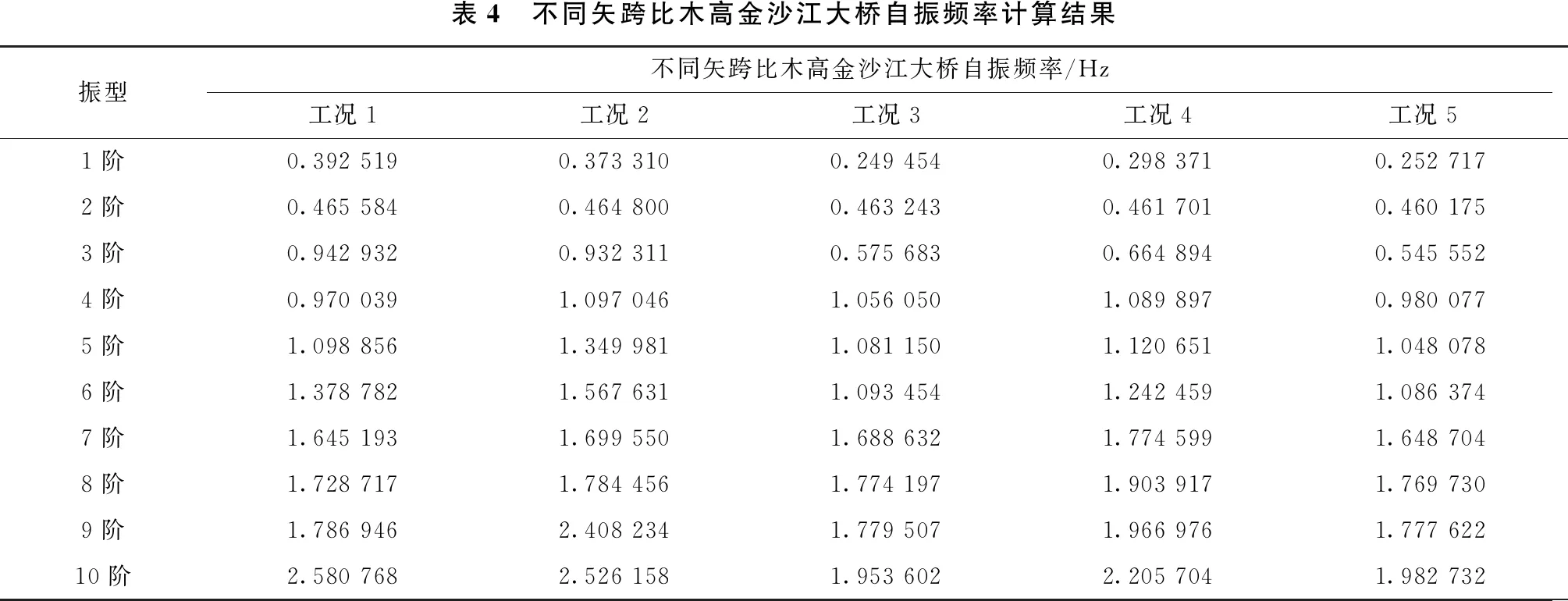
表4 不同矢跨比木高金沙江大桥自振频率计算结果振型不同矢跨比木高金沙江大桥自振频率/Hz工况1工况2工况3工况4工况51阶0.392 5190.373 3100.249 4540.298 3710.252 7172阶0.465 5840.464 8000.463 2430.461 7010.460 1753阶0.942 9320.932 3110.575 6830.664 8940.545 5524阶0.970 0391.097 0461.056 0501.089 8970.980 0775阶1.098 8561.349 9811.081 1501.120 6511.048 0786阶1.378 7821.567 6311.093 4541.242 4591.086 3747阶1.645 1931.699 5501.688 6321.774 5991.648 7048阶1.728 7171.784 4561.774 1971.903 9171.769 7309阶1.786 9462.408 2341.779 5071.966 9761.777 62210阶2.580 7682.526 1581.953 6022.205 7041.982 732

通过对5种工况下木高金沙江大桥自振频率计算结果(见表4)及各工况振型描述(见表5)对比分析可知：

1)随着矢跨比增大，各工况1阶自振频率整体呈现减小的趋势(如图5所示)，说明矢跨比的减小能够增大拱桥刚度，但矢跨比并不是越大越好，其在0.1～0.2附近基频较大，整体刚度较好。

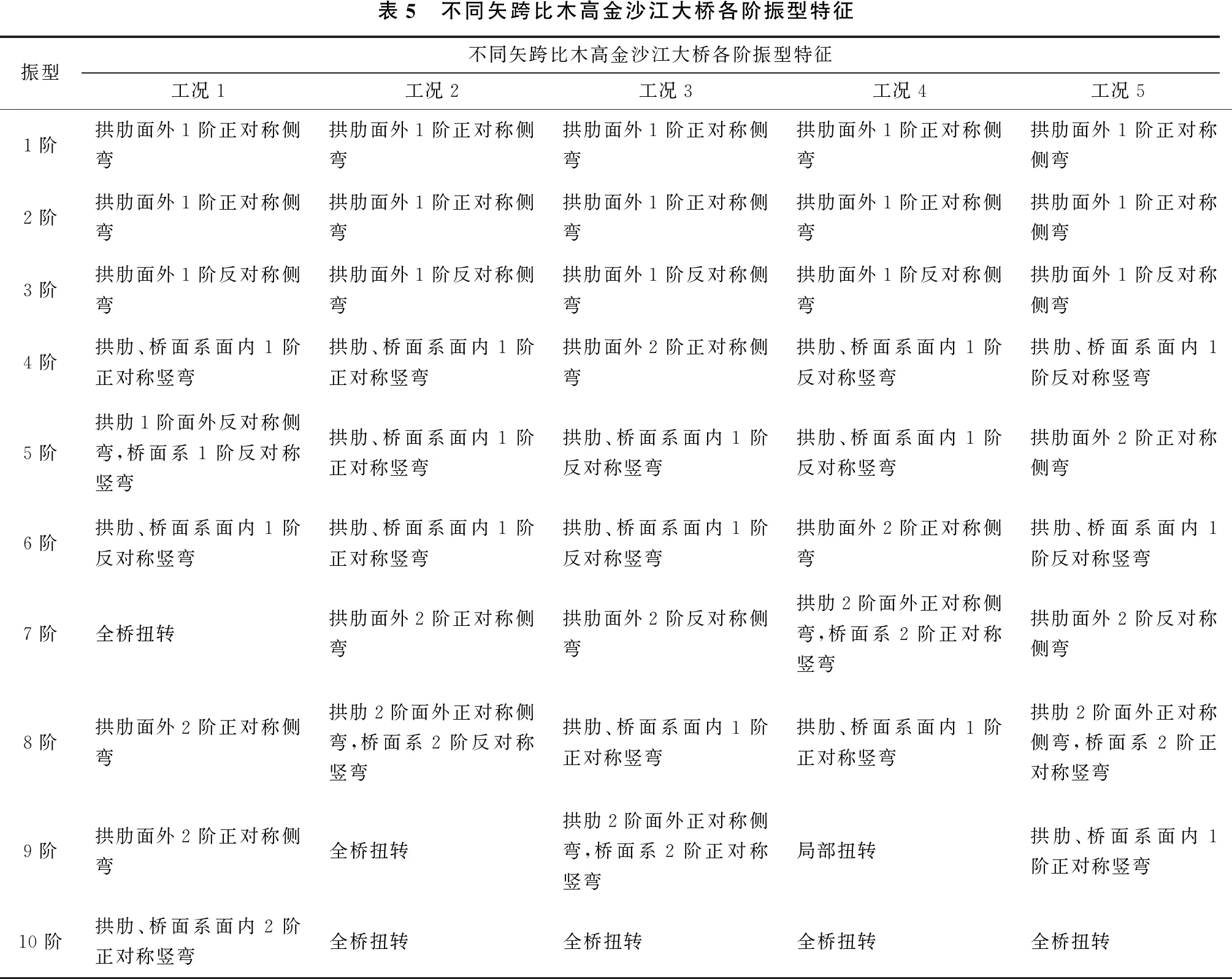
表5 不同矢跨比木高金沙江大桥各阶振型特征振型不同矢跨比木高金沙江大桥各阶振型特征工况1工况2工况3工况4工况51阶拱肋面外1阶正对称侧弯拱肋面外1阶正对称侧弯拱肋面外1阶正对称侧弯拱肋面外1阶正对称侧弯拱肋面外1阶正对称侧弯2阶拱肋面外1阶正对称侧弯拱肋面外1阶正对称侧弯拱肋面外1阶正对称侧弯拱肋面外1阶正对称侧弯拱肋面外1阶正对称侧弯3阶拱肋面外1阶反对称侧弯拱肋面外1阶反对称侧弯拱肋面外1阶反对称侧弯拱肋面外1阶反对称侧弯拱肋面外1阶反对称侧弯4阶拱肋、桥面系面内1阶正对称竖弯拱肋、桥面系面内1阶正对称竖弯拱肋面外2阶正对称侧弯拱肋、桥面系面内1阶反对称竖弯拱肋、桥面系面内1阶反对称竖弯5阶拱肋1阶面外反对称侧弯,桥面系1阶反对称竖弯拱肋、桥面系面内1阶正对称竖弯拱肋、桥面系面内1阶反对称竖弯拱肋、桥面系面内1阶反对称竖弯拱肋面外2阶正对称侧弯6阶拱肋、桥面系面内1阶反对称竖弯拱肋、桥面系面内1阶正对称竖弯拱肋、桥面系面内1阶反对称竖弯拱肋面外2阶正对称侧弯拱肋、桥面系面内1阶反对称竖弯7阶全桥扭转拱肋面外2阶正对称侧弯拱肋面外2阶反对称侧弯拱肋2阶面外正对称侧弯,桥面系2阶正对称竖弯拱肋面外2阶反对称侧弯8阶拱肋面外2阶正对称侧弯拱肋2阶面外正对称侧弯,桥面系2阶反对称竖弯拱肋、桥面系面内1阶正对称竖弯拱肋、桥面系面内1阶正对称竖弯拱肋2阶面外正对称侧弯,桥面系2阶正对称竖弯9阶拱肋面外2阶正对称侧弯全桥扭转拱肋2阶面外正对称侧弯,桥面系2阶正对称竖弯局部扭转拱肋、桥面系面内1阶正对称竖弯10阶拱肋、桥面系面内2阶正对称竖弯全桥扭转全桥扭转全桥扭转全桥扭转

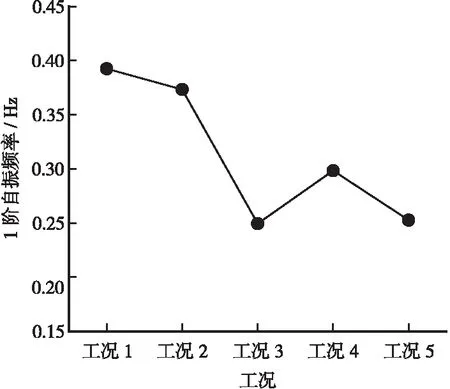
图5 不同矢跨比与拱桥自振频率变化关系曲线

2)对比发现，拱桥低阶发生面外振动，接着发生面内竖弯，最后发生全桥扭转，说明面外刚度较小，扭转刚度较大，符合钢管混凝土拱桥的振动形式，而且面外振型都是正反对称交替出现，这是因为木高金沙江大桥为对称体系，对称体系振动一般是正反对称交替出现。

3)从表4结果分析还发现，矢跨比对拱桥的面内竖弯基频和扭转影响较大，对拱桥的面外基频影响较小。例如，工况5(矢跨比为0.4)的第1阶面外基频为0.252717，工况1(矢跨比为0.05)第1阶面外基频为0.392519，面外基频改变幅度约为14%；工况1(矢跨比为0.05)第7阶全桥扭转基频为 1.645193，工况2(矢跨比为0.1)第10阶的全桥扭转基频为2.526158，全桥扭转基频改变幅度约为53%。这是因为改变矢跨比，会改变拱中轴力的大小，轴力会影响结构的几何刚度，就会改变拱桥的面内刚度和面外刚度。

3.4 矢跨比对拱桥稳定性影响分析

不同矢跨比对拱桥稳定性系数计算结果如表6所示，从表6可以看出，随着矢跨比的增加，稳定安全系数持续增加，矢跨比从0.05增加至0.3，拱桥的安全系数与矢跨比基本上呈线性关系增加(如图6所示)，但当矢跨比大于0.3时，拱桥的稳定安全系数增加不明显，说明矢跨比并非越大越好。从计算结果分析可知，矢跨比为0.2～0.3，拱桥的稳定系数较为合理。

通过对5种工况计算结果分析发现，拱桥的失稳模态均为面外失稳，这主要是因为拱桥的拱肋是一个压弯受力构件，同时受竖向力和横向力作用，当拱桥受横向力的作用时，拱桥拱肋的横向联系较弱，故失稳模态常常表现为面外失稳，因此，对于哑铃型截面拱桥需要加强拱肋的横向联系，以确保整桥的稳定性。

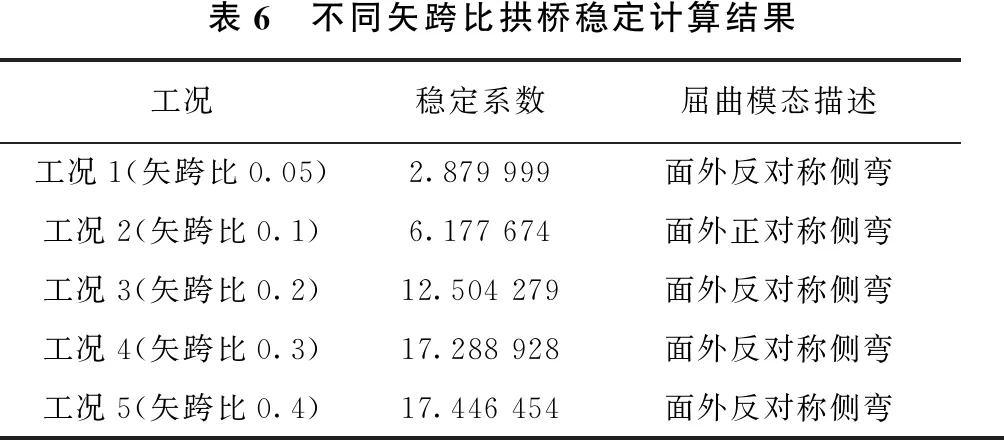
表6 不同矢跨比拱桥稳定计算结果工况稳定系数屈曲模态描述工况1(矢跨比0.05)2.879 999面外反对称侧弯工况2(矢跨比0.1)6.177 674面外正对称侧弯工况3(矢跨比0.2)12.504 279面外反对称侧弯工况4(矢跨比0.3)17.288 928面外反对称侧弯工况5(矢跨比0.4)17.446 454面外反对称侧弯

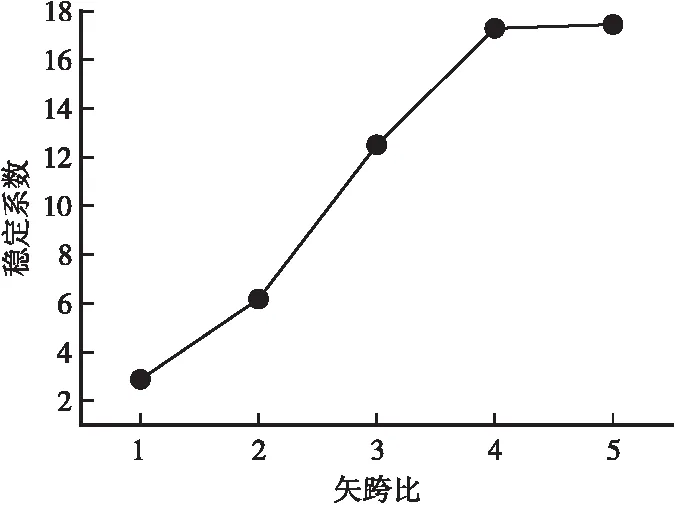
图6 不同矢跨比与拱桥稳定系数变化曲线

4 结论

以木高金沙江大桥为研究背景，采用有限元方法建立了哑铃型截面拱桥的三维计算模型，研究了拱肋横撑布置形式、矢跨比对哑铃型拱桥动力特性及稳定性的影响，主要结论如下：

1) 计算结果对比发现，临近拱脚处设置为“K”撑和“米”撑的拱桥稳定系数分别比设置为一撑的拱桥安全系数增加57%和78%，说明拱桥的横撑形式可以明显提高拱肋的刚度，改变横撑布置形式对于提升拱桥的整体稳定性有显著影响。

2) 计算结果表明，不同横撑布置形式下拱桥屈曲模态前3阶均为面外失稳，第4阶才出现面内失稳，说明钢管混凝土拱桥的面外失稳是哑铃型拱桥的主要问题，在设计施工中应重点考虑此类桥型的面外失稳。此外，拱肋在1/4跨径处和跨中处相对错动变形较大，说明这两处是钢管混凝土拱桥容易发生面外失稳的地方，因此，应增强木高金沙江大桥拱肋1/4跨径处和跨中处的横向联系。

3) 随着矢跨比增大，拱桥第1阶自振频率整体呈现减小趋势，矢跨比为0.1～0.2时，拱桥的基频较大，整体刚度较好。拱桥稳定系数一开始基本上随着矢跨比的增大而呈线性增加，但当矢跨比大于0.3时，拱桥的稳定系数增加不明显。因此，木高金沙江大桥的矢跨比为0.2～0.3较为合理。