DC-DC全桥电路软启动控制方法

李源升，薛梦娇，胡朋举

(国网新疆电力有限公司超高压分公司，新疆 乌鲁木齐 830092)

随着社会能源需求的增长，社会高速可持续发展的能源结构不再仅仅依靠单一的化石能源，为了应对这一问题，我国一直积极发展新能源，新型清洁能源是今后的发展趋势，当今能源结构多样化越来越明显。而人类生产生活所需求的载能体也呈现多样化趋势。为了促进能源网络的发展，实现社会的可持续发展，能源互联网成为目前研究能源形式的热点[1]。

传统的桥式直流变换器是将输入侧能量传输到输出侧，而且是单向的能量流动。只能将能量由一端向另外一端传输，而双向DC-DC变换器可以在同一设备上实现能量的双向传输。早在20世纪80年代初，为了减轻人造卫星太阳能电源系统的体积和质量，就有学者提出用双向Buck/Boost 变换器与太阳能电池的组合代替蓄电池供电[2]。华中科技大学研究团队针对电力电子变压器对配电系统的控制性能及动态特性的影响进行了理论与仿真研究[3]。清华大学研究团队针对柔性直流配电网的直流固态变压器方案进行了研究，并对其基本结构、控制策略及能量管理系统做了分析验证[3]。赵争鸣教授提出了直接基于能量平衡关系的电能路由器控制策略，并对其正确性进行了试验验证[4]。

目前研究热点主要集中在改进的变换器拓扑结构及移相控制方法，但是还存在许多不足[5]。前文重点研究方向在于，尽量减小系统的回流功率，降低开关管的单管电压应力、电流应力等方向，鲜有分析系统启动过程中出现大电流的现象。本文在单移相控制的基础上针对启动过程中出现的大电流进行分析[6-12]，提出改进方法，解决系统启动过程中所出现的大电流现象。减少了启动过程中出现的大电流，改善了系统的可靠性和安全性。同时使用数字处理器实现双向DC-DC变换器的移相闭环控制。

1 DC-DC全桥电源系统控制器设计

1.1 DC-DC全桥电源的工作原理

图1中，变压器两侧全桥每个桥臂的上下管之间都是180°互补导通，斜对角2只开关管之间的脉冲信号相同。变压器左侧全桥逆变输出的电压均为固定占空比的双极性方波，右侧全桥折算到变压器左侧的电压也为固定占空比的双极性方波，两侧方波之间有相角差。单移相控制方式就是通过控制变压器两侧绕组之间的移相角来实现功率的大小变化和方向的流动。

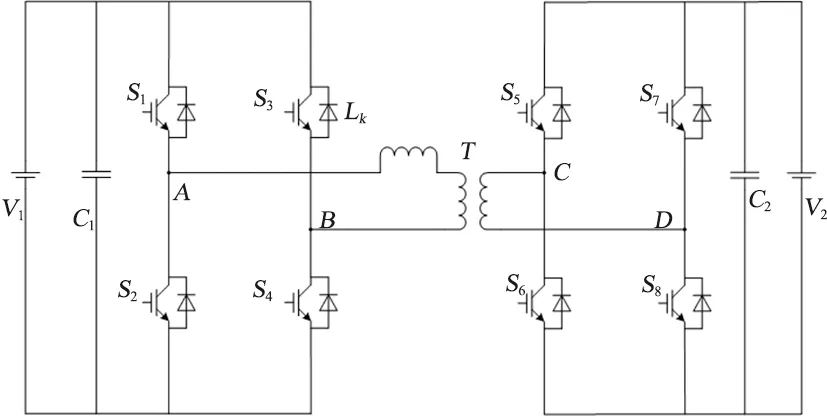
图1 双向全桥拓扑结构

单移相下的能量正向流动中，DAB模块是从左侧流向右侧，即UAB的相位超前UCD；同理，单移相下的能量负向流动中，能量从右侧流向左侧，即UAB的相位滞后UCD。为了便于分析，进一步简化全桥DC-DC电路的变压器，可以得到变压器的等效电路，同时图1所示的全桥DC-DC电路可以简化为图2所示的DAB能量流动电路模型[13-15]。由图2可知，全桥DC-DC电路的能量双向传递与储存主要是靠这个功率电感以及变压器内部的漏感。通过图2可以对单移相控制下DAB电路的正向能量流动的工作模式进行具体分析。

图2 DAB的等效电路模型

在单移相控制下，一个开关周期内DC-DC变换器的稳态电感电流可以分为4个阶段[16-17]，若令t0=0，则t1-t6时刻可以分别表示为t2=DT，t3=T，t5=(1+D)T，t6=2T，D为移相占空比，0≤D≤1。根据伏秒平衡原理，即电感电流的对称性，即iL(t0)= -iL(t3)。

(1)

(2)

式中：V1和V2分别为变换器输入侧和输出侧的电压；n为变压器变比；L为等效电感，是串联电感和变压器漏感之和。则有：

(3)

(4)

设交换器的电压调节比k=V1/V2，开关频率fs=1/(2T)，则有：

(5)

(6)

相应可得到单移相控制方式下传输功率为

(7)

则有DC-DC变换器的输出平均电流为

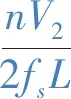
(8)

流经变换器等效电感L的电流峰值为

(9)

通过式(9)可知，传输功率的范围会随移相占空比改变而发生改变。为了便于分析，将传输功率标幺化，定基准值为

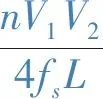
(10)

则此时传输功率的标幺值为

(11)

1.2 DC-DC全桥电源的软启动

当从低压侧启动时，电容C2的电压为0，漏感电流会出现较大的冲击。电路在半个周期内占空比由0逐渐增加到0.5，因此其半周期的伏秒值为

(12)

式中：n为变压器的匝比，n=n2/n1；D为移相比；T为半个开关周期。

由此可见，从0开始缓慢增加占空比D，电压半周期伏秒值从0增加，从而有效减小漏感冲击电流。该启动方式的波形如图3所示，即改变加在各个开关管上的驱动脉冲宽度，在系统未达到稳定前，动态调节驱动脉冲宽度，限制电感电流的上升时间，使电感电流工作在DCM模式，从而将电流限制在一定范围内，有效降低单个开关管的电流应力。

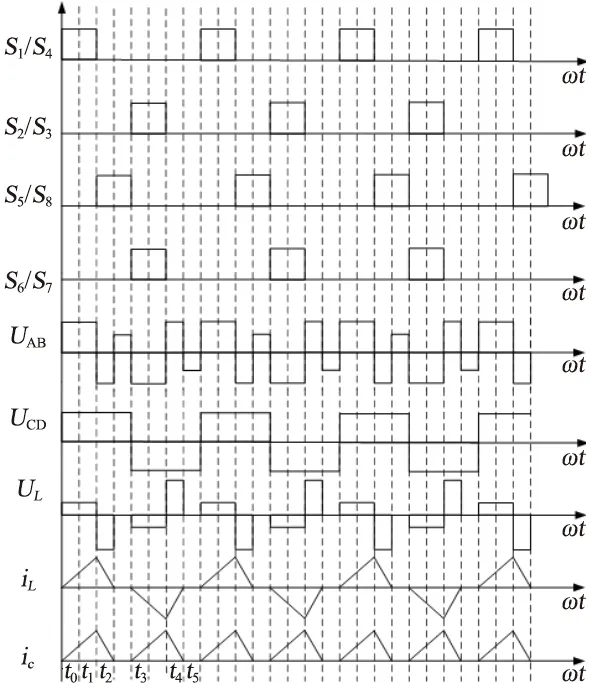
图3 窄脉宽启动过程

1.3 死区影响分析及补偿措施

在变换器工作时，为了避免同一桥臂的上下开关管同时导通造成短路，致使电路无法正常工作，一般要设置一个死区时间，这对电路工作的可靠性十分重要，但是死区会造成波形变化和传递功率大小变化。以功率正向传输为例，设置一个死区时间tdb。当i(t0)<0且i(t2)<0时，两侧工作模态如图4所示。D为DAB模块的低压侧原边全桥与高压侧副边全桥开关管之间的驱动信号的移相比，由图4可知，t0-t2时刻，DAB模块的电流在t0时刻之前，it0<0,t0时刻后，变压器原边电流经S1、S4上的体二极管，此时电路原边侧输出的电压UAB与原边侧的输入电压相同，即UAB的高电平比S1、S4的驱动脉冲提前死区时间tdb。it2<0，高压侧副边电路的开关管S6、S7的二极管需要进行续流，同时开关管S5和S8不导通。因此，死区影响下的实际移相比为Dt=D+tdb/T。因此，当移相比D=0 时，由于死区时间的存在，Dt=tdb/T，系统仍会输出功率。当i(t0)<0且i(t2)>0时，即前文分析的正常稳定工作时的情况，此时死区时间对实际的移相占空比没有影响，Dt=D。

图4 死区时间对于移相比的影响(i(t0)<0, i(t2)<0)

当i(t0)>0且i(t2)>0时，两侧工作模态如图5所示。实际的移相占空比为Dt=D-tdb/T。由于i(t0)>0，故在S1、S4没有给驱动信号时，原边电流通过开关管S2、S3并联的二级管续流，UAB的高电平与S1、S4的驱动脉冲相比，减少了死区时间tdb，而由于i(t2)>0，故在S5、S8没有给驱动信号时，副边的电流通过开关管S6、S7的体二极管进行续流，UCD的高电平与S5、S8的驱动脉冲同步，因此，死区影响下的实际移相比Dt=D-tdb/T，实际移相比小于理论值。

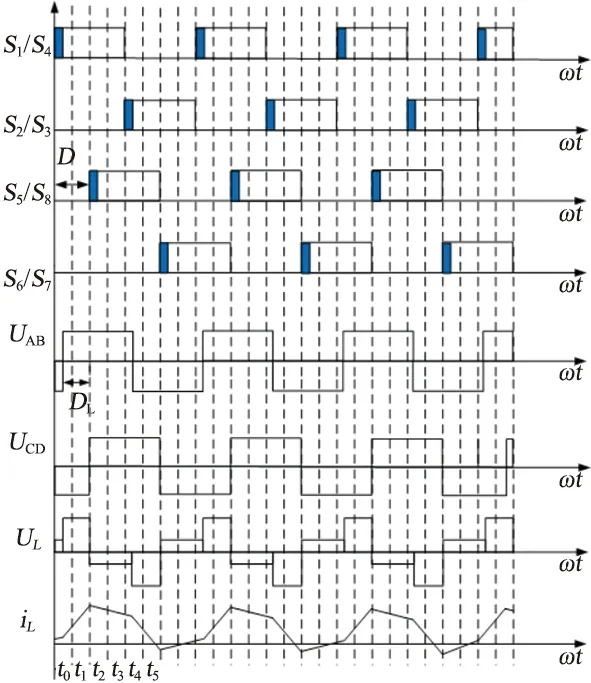
图5 死区时间对于移相比的影响(i(t0)>0, i(t2)>0)

系统仿真的输出功率是完全理想情况下，然而实际开关管的死区影响输出功率，而且随着电流变化而改变，当死区时间tdb越来越大时，死区影响将增加。因此需要采取补偿措施。DAB模块工作在i(t0)<0且i(t2)<0时，加上死区的实际移相比为Dt=D+tdb/T，此时应使S5、S7的驱动信号相对于S1、S3的驱动信号滞后，时间比理论减小tdb即可。DAB模块工作在i(t0)<0且i(t2)>0时，实际移相比为Dt=D，此时开关管不用死区补偿，而且开关管容易实现软开关状态。DAB模块工作在i(t0)>0且i(t2)>0时，实际的移相比为Dt=D-tdb/T，此时应使S5、S7的驱动信号相对于S1、S3的驱动信号滞后时间比理论增加tdb即可。

1.4 电压闭环控制

双向DC-DC全桥电路的开关频率大，普通设备难以在极小时间内同时采样得出电压、电流的波形，采样难度大。因此本文的控制方式采用电压单闭环的控制方式，将采样电压作为闭环的被控对象，利用改变占空比来影响电压的大小，从而影响电流大小，进行控制整个电路的稳定。

由前文有输出与输入控制量之间传递函数为

(13)

试验中参数取值为U1=48、n=8、fs=25 kHz、C2=470 μF、Ro=250 Ω、D=0.2、L=8 μH。则加入调节器前，系统开环传递函数为

(14)

图6的Bode图是根据式(14)中传递函数得出，在系统加入调节器前，该系统是稳定系统，但可以明显看出在低频段时，系统的増益过小，从而导致系统稳态精度不佳，存在稳态误差。而系统的动态响应因截止频率过低而过慢。对于改善系统的性能有多种方法，本论文通过加入快速PI调节器，利用Bode图进行系统优化。为消除低频情况下的缺点，PI调节器零点接近系统的低频极点，能够解决低频极点对系统的影响。

加入快速PI调节器后的系统Bode图如图7所示，PI调节器含有积分项，一定程度上提高了系统稳态精度，系统动态响应快。经过实际仿真验证，得出Kp=0.01，Ki=90。

1.5 系统控制结构

经过对DAB模块的工作原理进行分析，在单移相控制的基础上进行了详细分析，并且搭建了1台1 kW的双向DC-DC变换器样机，为了验证隔离性双向DC-DC电路在此控制方式下的正确性，具体的技术要求和系统参数如下：DAB模块的额定输出功率Pn=1 kW；直流母线电压(低压侧)VL=48 V，变化范围48±10%；直流母线电压(高压侧)VH=400 V，变化范围400±10%；开关频率fs=25 kHz；低压侧母线电容C1=4700 μF/100 V；高压侧母线电容C2=470 μF/450 V。

控制系统的整体控制框如图8所示，包括主功率电路、控制电路、调理电路、驱动电路等。

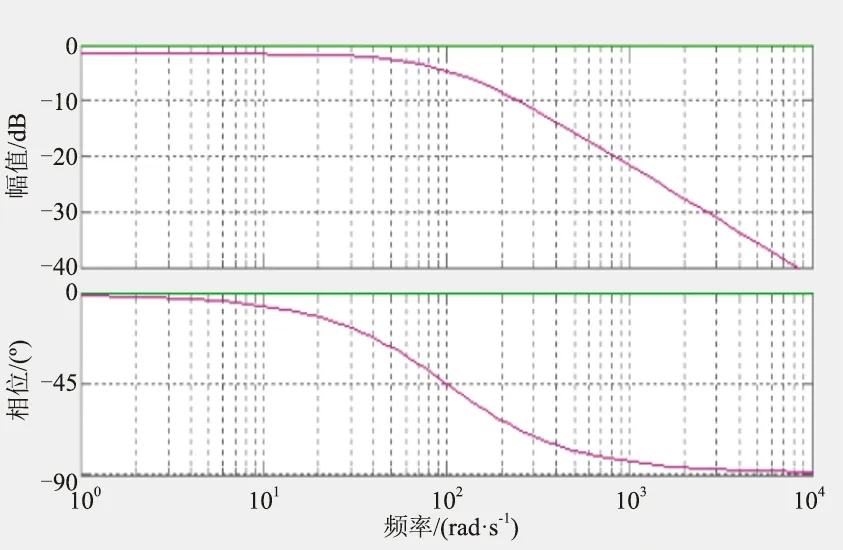
图6 系统开环Bode图

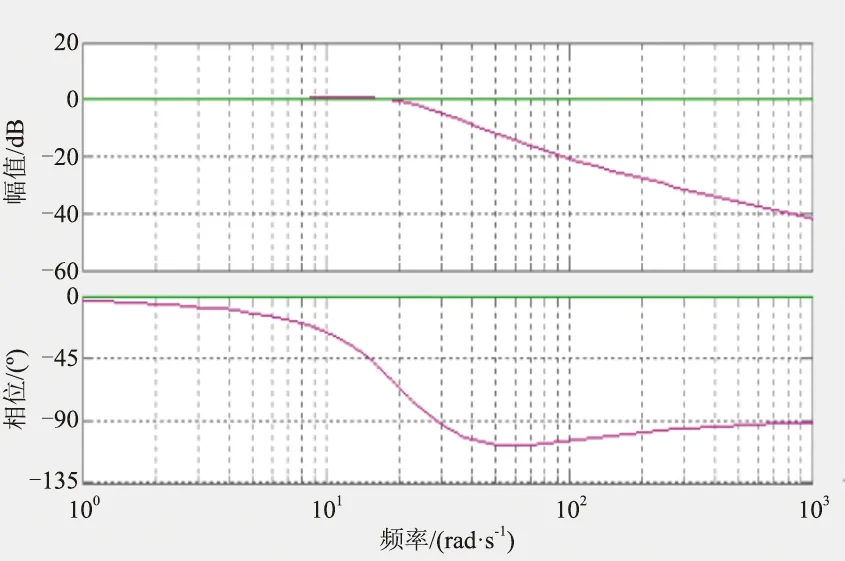
图7 系统补偿后Bode图

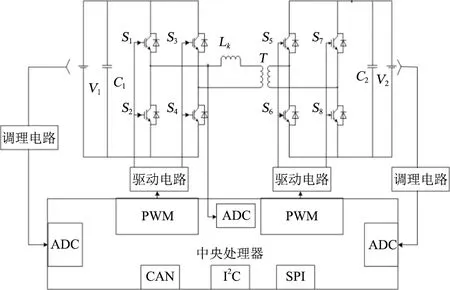
图8 系统控制结构框图

2 仿真及试验结果分析

2.1 PLECS仿真及结果分析

本系统以25 kHz DC-DC电源为背景进行仿真研究。采用上述方案构建DC-DC电源的闭环控制系统，在PLECS仿真环境下进行仿真分析。系统的仿真参数如下：输出电压380 V，直流母线电压VDC=48 V，电感L=10 μH，电容C=440 μF，三角载波频率fs=25 kHz。外环调节器的PI参数：kp1=1.75，ki1=20。

对所设计的DC-DC电源分别做启动(负载电阻R=250 Ω)和稳态过程负载(负载电阻R=250 Ω)仿真。

图9与图10对比了系统在启动和稳定状态下两侧全桥输出侧电压波形，启动过程中，两侧电压基本同向，从而限制启动过程中的冲击电流。在系统稳定后，系统以一个固定的移向角运行。

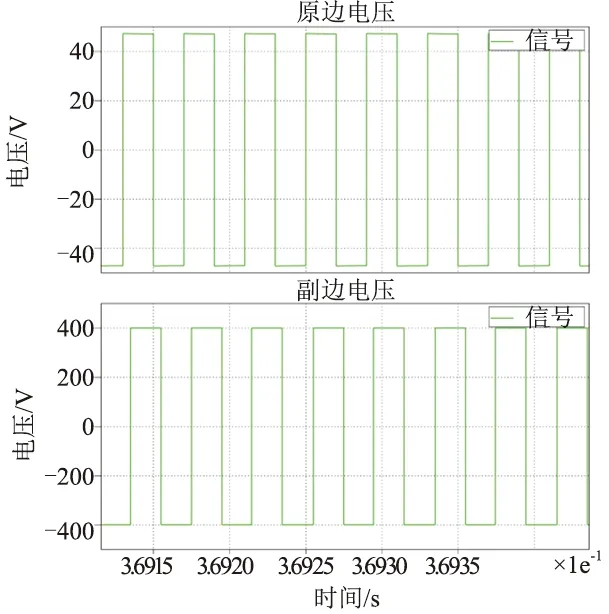
图9 启动过程波形

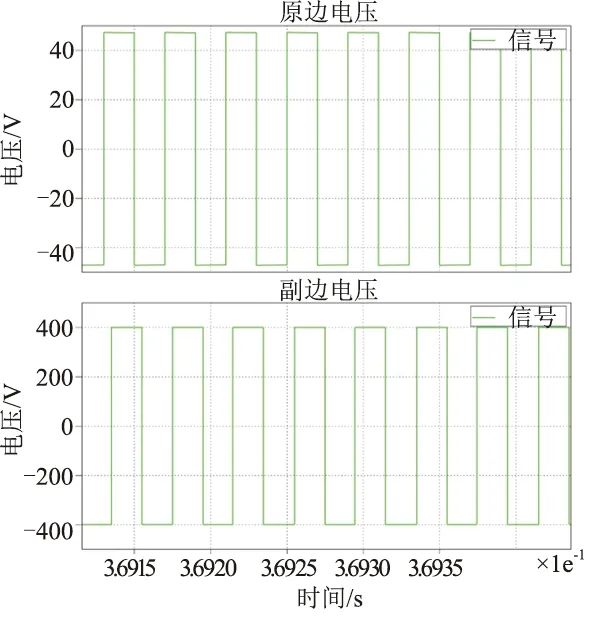
图10 稳态输出波形

图11与图12对比了系统在启动和稳定状态下变压器两侧电压和电流波形，启动过程中，副边电压为逐渐增加的方波，流过变压器的电流也由三角波逐渐变为梯形波，系统最后逐步稳定下来，在负载不变的前提下，以固定移相角运行。

图13、图14与图15分别为软启动电压电流波形、软启动功率电感电压波形与软启动状态下负载突变时电压波形。由图13可知，软启动状态下电压电流缓慢增加，有利于减少电压电流突变导致的电流过大或者短时电压过大对开关管的冲击，一定程度上减少了纹波电流对开关电源的冲击影响。

由图14可知，电感电压缓慢增大，减少了电压突变对电路稳定性造成的影响，一定程度上减少了电压对开关管及供电电源冲击，使其寿命增加。

图15为负载突变时电压波形，由图15可知，在软启动作用下，系统的超调仅有0.92%。调节时间较短，而且最大峰值电压只超出额定电压2.8 V，对开关管的冲击基本可以忽略不计，验证了该启动方式具有良好的快速性能。

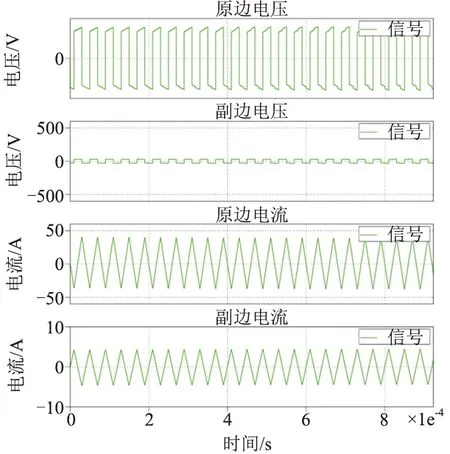
图11 启动过程时电流波形

图12 稳态时电流波形

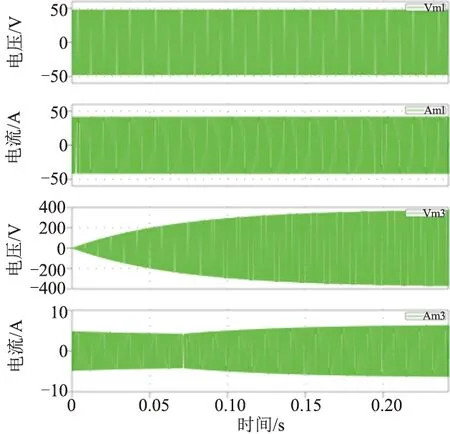
图13 软启动电压波形

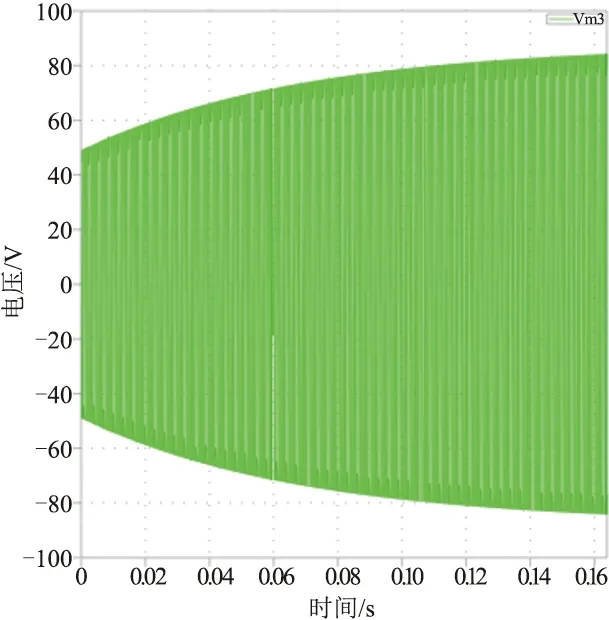
图14 软启动功率电感电压波形

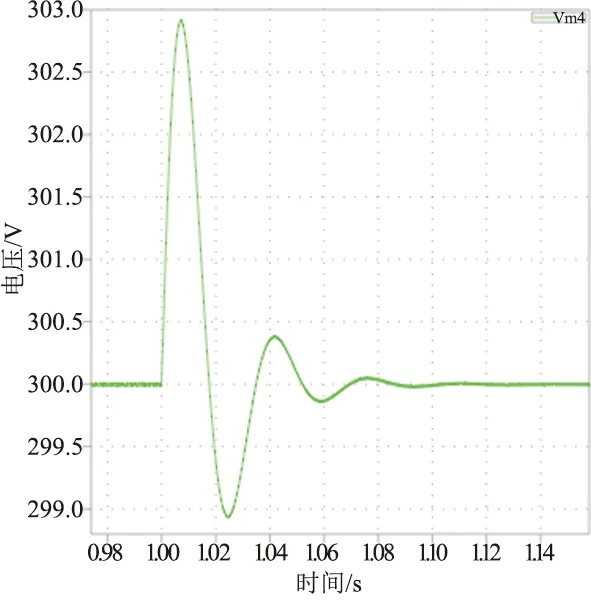
图15 软启动状态下负载突变时电压波形

2.2 试验结果分析

本系统以DSP为核心，使用TI官方提供的编程软件Code Composer Studio 6.0进行软件算法的编程，实现对全桥DC-DC的闭环控制。利用上述控制方法搭建试验平台，试验参数如表1所示，图16为试验平台。

表1 试验主电路参数

试验波形如图17所示。图17为开关管实现ZVS软开关；图18为直接启动与软启动波形。图17为开关管ZVS(zero voltage switch)导通波形，蓝色为驱动信号波形，绿色为相应IGBT上CE之间电压波形，由图17可知，IGBT在未给驱动信号前，两侧电压已经为零，因而，该开关管可以实现零电压导通，开通损耗几乎为零。功率回路中的8个开关管均可实现零电压导通。

图18为系统正常启动时系统输出电压波形，系统输出电压逐渐稳定到400 V。

图16 试验平台

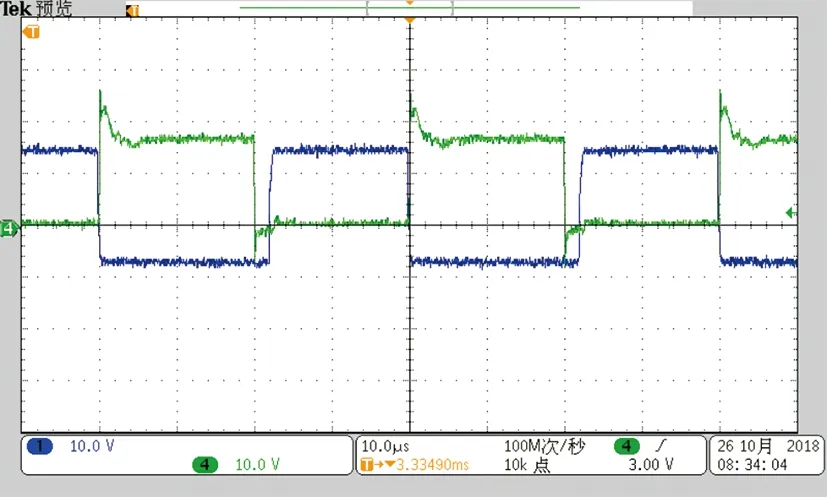
图17 开关管实现ZVS软开关

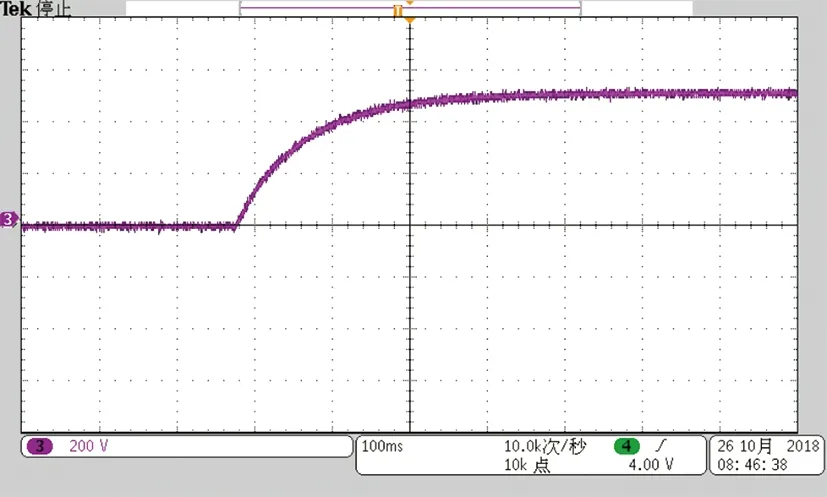
图18 直接启动电压波形

图19为系统软启动波形，在启动的前半段，由于采用了软启动策略，限制了电路中的电流，也就限制了高压侧电容的充电电流。

由图19可知，软启动过程中，前半部分由于充电电流被限制，电压缓慢上升，待达到设定电压后，系统进入闭环控制状态，将PWM波的占空比固定在0.5，动态调节移相角度。稳定输出电压波形。使电压逐渐稳定到400 V。系统稳定时间稍长，但相比较于直接启动，限制了系统的冲击电流，减小了系统中的电流应力。保证了系统运行的安全性。

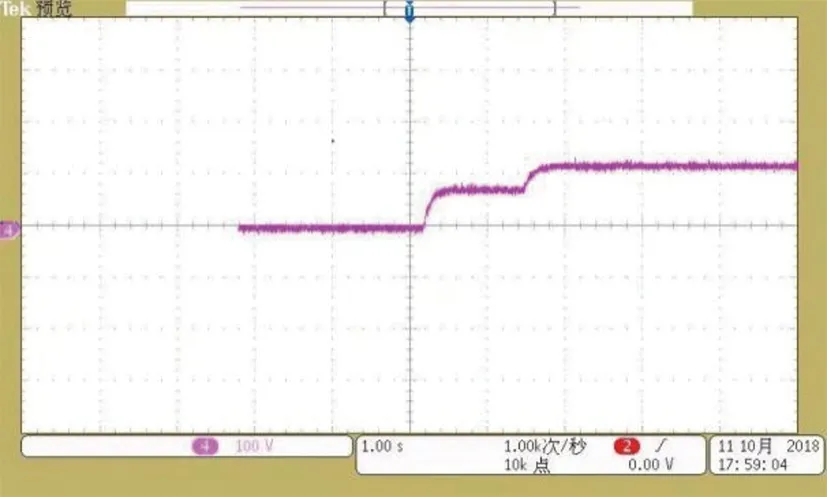
图19 软启动电压波形

3 结语

本文以单相全桥DC-DC电源作为研究对象，对双向全桥直流变换器进行建模，得出系统的传递函数，对开环系统进行补偿，有效改善了系统的稳定性。针对系统启动过程中出现的短暂冲击电流，分析了冲击电流的成因，提出了动态改脉宽的软启动控制方式，较串电阻、加辅助回路等方式具有成本低，控制简单等优点。系统进入稳态运行后，采用闭环控制策略维持电压稳定。最后对实际工程中出现的死区对系统输出的影响进行了具体分析，并针对具体情况，提出了相应的补偿措施。此外，系统仿真和试验结果表明，本文采用的控制方法有效可行，提高了电源的输出精度及响应速度。