吊装环境下塔类设备局部应力及参数影响性分析

张朝明，詹忠锜，范 磊，郭甲俊，徐艳红，王会乾

(中建安装集团有限公司，江苏 南京 210000)

大型塔类设备的吊装是工程施工中的一个重要环节【1】。在吊装过程中，由于设备质量和直径大、跨度长，不仅需要关注结构整体的变形及应力，同时也需要关注吊耳整体强度以及吊耳与筒体接触区域的局部应力。因此如何合理高效地设计吊耳尺寸，并在控制工程造价的前提下，保证结构稳定可靠、筒体局部应力不超限、不产生塑性破坏是吊耳设计选型的主要考量。

吊耳局部应力计算一般有规范理论计算【2-4】和有限元分析两种方法。牛龙哲【5】采用现有各种规范及Ansys仿真对超大型立式塔器轴式吊耳进行局部应力计算分析，但其有限元计算结果并未分离薄膜应力及表面应力，仅从变化趋势及应力数量级方面与现有规范进行了对比；刘宏超【6】、张微【7】等分别采用SW6—2011软件及有限元软件分析了轴式吊耳起吊过程中的薄膜应力及表面应力；王非【8】采用WRC 107和有限元法分析了轴式吊耳在水平及竖直状态下的受力情况，并对垫板间隙及加厚段进行了优化设计。上述研究重点关注了轴式吊耳的受力及筒体局部应力，但对于吊耳尺寸参数变化及板式吊耳的研究涉及较少。而现有规范【9】仅能计算长宽比小于4的矩形附件和圆形附件，无法对一般板式吊耳进行局部应力计算。

针对现有板式吊耳难以根据规范计算局部应力，或有限元计算结果难以指导实际设计的问题，建立三维实体有限元模型，充分考虑模型的边界效应，采用路径应力线性化的方法计算筒体的薄膜应力、表面应力，并基于此分析不同吊耳参数及荷载参数下的吊耳局部应力。同时，采用正交实验、多因素方差分析确定不同参数对局部应力的影响权重。

1 吊耳局部应力分析模型

1.1 模型介绍

以某项目丙烯精馏塔设备实际吊装为例进行分析。丙烯精馏塔结构如图1所示。该塔塔体高度为67 950 mm，塔体内径为φ9 200 mm/φ11 000 mm。主吊为轴式吊耳，质心高度为63 900 mm。局部应力分析模型主要由筒体、连接件和吊耳组成，分析工况为水平起吊，吊索与吊耳夹角为0°。各部件间通过“Tie”进行连接。管轴式吊耳局部应力有限元模型如图2所示。为方便计算结果分析对比，模型中对吊耳进行相应简化。不考虑吊耳焊接材料强度变化，默认其强度与吊耳强度一致。由于起吊质量大，轴式吊耳自行设计，相关计算参数如表1所示。

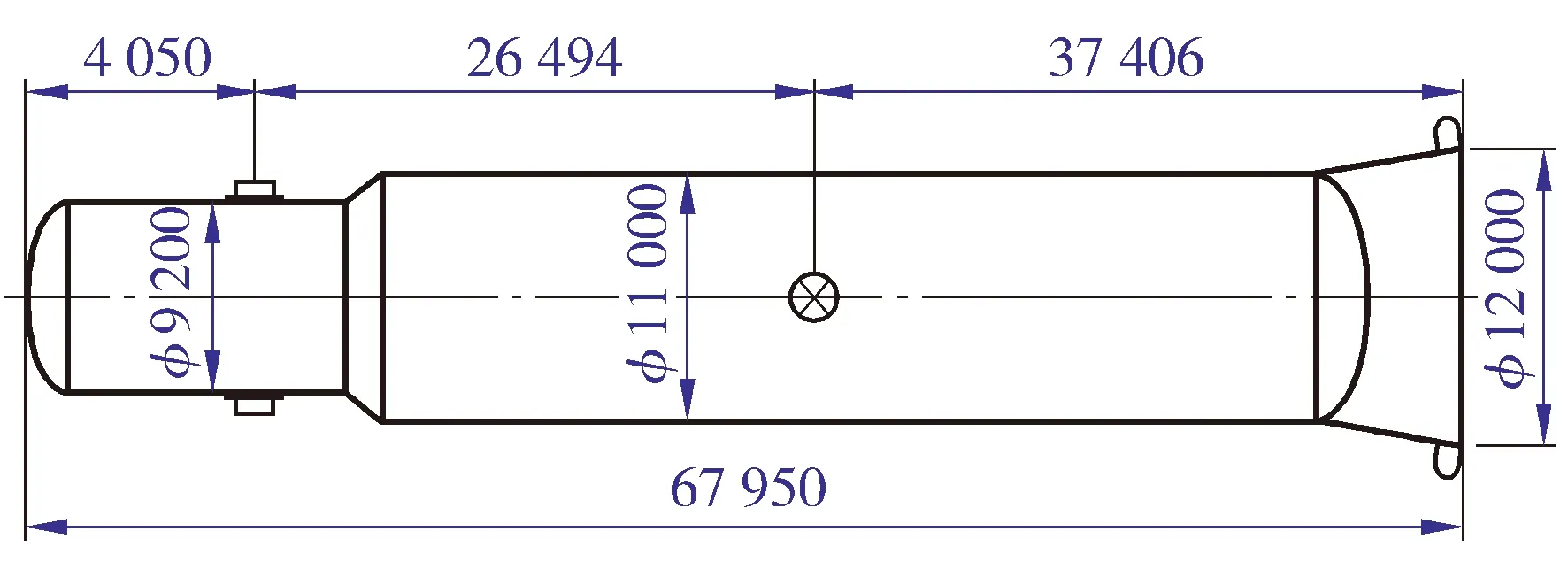
图1 丙烯精馏塔结构

图2 管轴式吊耳局部应力有限元模型

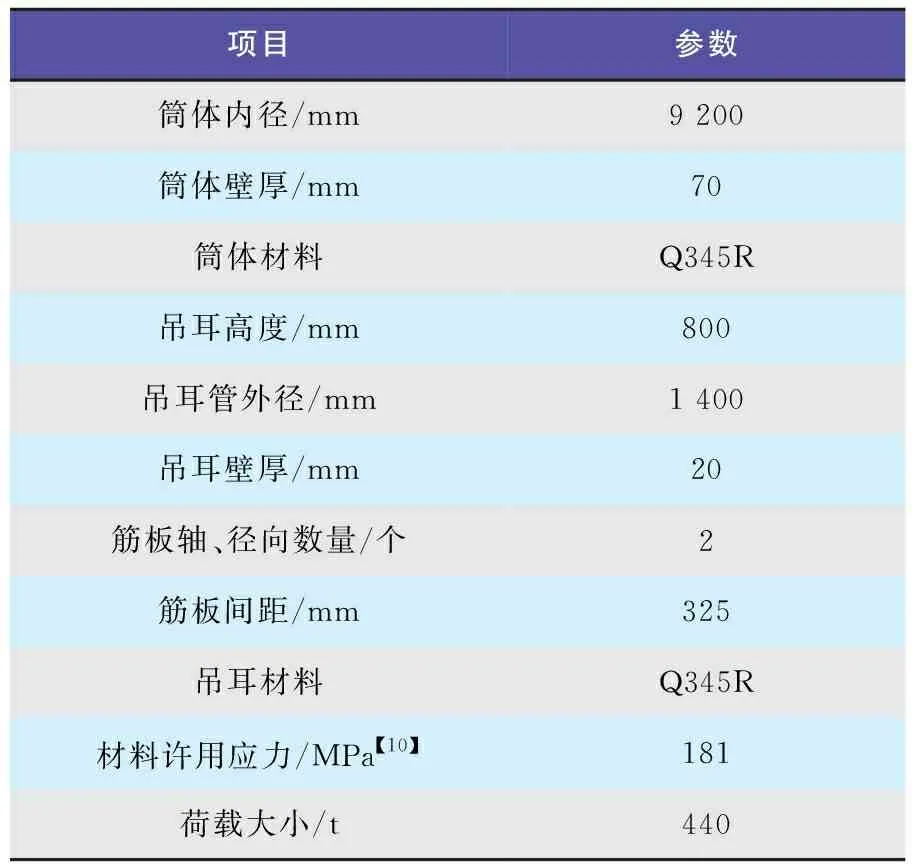
表1 模型尺寸及参数

一般而言，对于筒体壁厚与直径的比值小于1∶15的压力容器器壁可采用薄壳单元(M3D4R四结点四边形膜单元)进行有限元模拟，而对于具有明显复杂三维结构的吊耳只能采用实体单元(C3D8R)进行模拟【11】。

进行有限元计算时，由于薄壳单元与实体单元之间存在自由度不匹配的问题，往往使得转动自由度在连接的交界处产生不连续，进而造成交界处结构应力计算不准确，从而影响局部应力的计算【12】。故在本模型计算时，筒壁及吊耳均采用C3D8R实体单元进行离散化模拟。

当采用实体单元进行有限元分析时，一般来说，在横穿厚度的路径上应力分布不是线性的，通常的做法时将计算的应力沿着厚度方向进行应力线性化【13】，以便提取薄膜应力和弯曲应力。应力分类线的位置根据ASME Ⅷ的选取原则确定。基本方法是将应力分类线(SCL)的实际应力分布按照静力和静力矩等效原理处理沿着应力分类线恒定分布的薄膜应力和沿着应力分类线线性分布的弯曲应力【14】，即：

(1)

(2)

式中：σm——薄膜应力，MPa；

σb——弯曲应力,MPa；

σ——实际应力,MPa；

x——局部坐标系的x轴坐标,mm；

t——SCL长度,mm，本文指壁厚。

实际计算时需要将x、y和z方向的正应力和剪应力这6个应力分量分别进行应力线性化，得到各分量的薄膜应力和弯曲应力。再通过第三强度理论计算大主应力σ1、中主应力σ2和小主应力σ3【15】，进而得到Tresca应力，开展各类应力评定。根据《钢制压力容器—分析设计标准》(2005年确认)【16】、《化工设备吊耳设计选用规范》【17】，本文的主要评定内容如下：

SⅡ≤1.5KSm

(3)

SⅣ≤2.6Sm

(4)

式中：SⅡ——一次局部薄膜应力强度,MPa；

SⅣ——一次加二次应力强度,MPa；

K——荷载组合系数；

Sm——材料许用应力强度,MPa。

1.2 模型边界对计算结果的影响

不同的模型边界条件将直接影响模型计算结果的准确性。合理地设置边界条件可大大降低模型单元数量，提高模型计算效率，同时也能提高模型的计算准确度。为分析不同模型边界对计算结果的影响，共设以下4种模型边界，分别为全圆周、半圆周、1/4圆周和半对称结构，如图3所示。

图3 不同模型边界设置方法

不同边界条件下计算的模型最大Tresca应力及结构位移结果如表2所示。

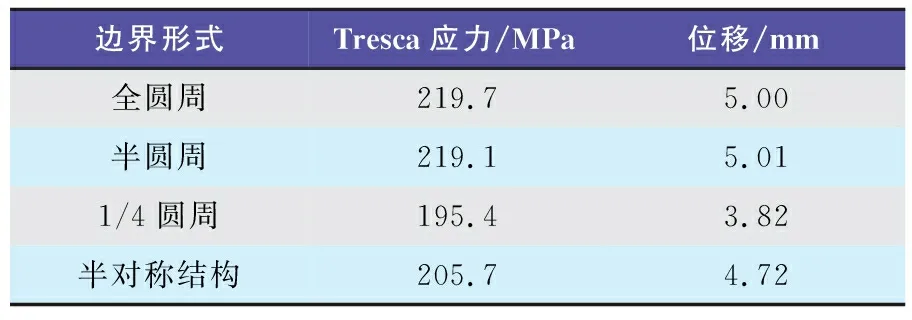
表2 不同边界条件下的筒体应力及变形结果

从表2中可以看出，在相同的起吊荷载下，采用半圆周边界条件与全圆周边界的计算结果几乎一致，在保证计算精度的同时节约近一半网格。而1/4圆周及半对称边界，由于约束过强，整体刚度较大，位移及应力均有明显降低。故在本文分析过程中主要采用半圆周边界对模型进行约束。

2 有限元与规范计算结果对比分析

将有限元计算结果推导出的薄膜应力、弯曲应力与规范方法计算结果进行进一步对比分析，从侧面验证模型的准确性，以便进行下一步吊耳参数影响性的分析。

首先，采用HG/T 20582—2020《钢制化工容器强度计算规范》(以下简称规范)【9】第19章中的方法对轴式吊耳局部应力进行计算，相关参数说明见规范，各参数示意见图4。

图4 规范计算参数示意

轴式吊耳起吊过程中，外荷载对圆筒引起的局部应力主要是由作用在吊耳上的横向剪力以及横向外力矩导致的。故薄膜应力可按式(5)～式(6)计算，剪应力可按式(7)计算(各式中的符号说明详见规范)：

(5)

(6)

(7)

计算得到吊耳周边圆筒上各点应力后，按式(8)取两者中的较大者作为复合应力强度σ。

(8)

按上述公式计算得到一次局部薄膜应力SⅡ=32.7 MPa，一次薄膜+弯曲+二次应力SⅣ=222.4 MPa。

其次，采用精细化有限元方法对起吊过程中的圆筒进行力学分析，荷载施加条件与规范计算时一致。Tresca应力云图如图5所示。由图5可知，吊耳根部最大应力为259.7 MPa，垫板根部最大应力为219.7 MPa。此处主要以垫板根部为例分析其局部应力。由图5可以确定圆筒上最大应力点，以该点为起点沿着筒壁厚方向设置应力分类线，如图6所示。

图5 吊装力作用下轴式吊耳Tresca应力云图

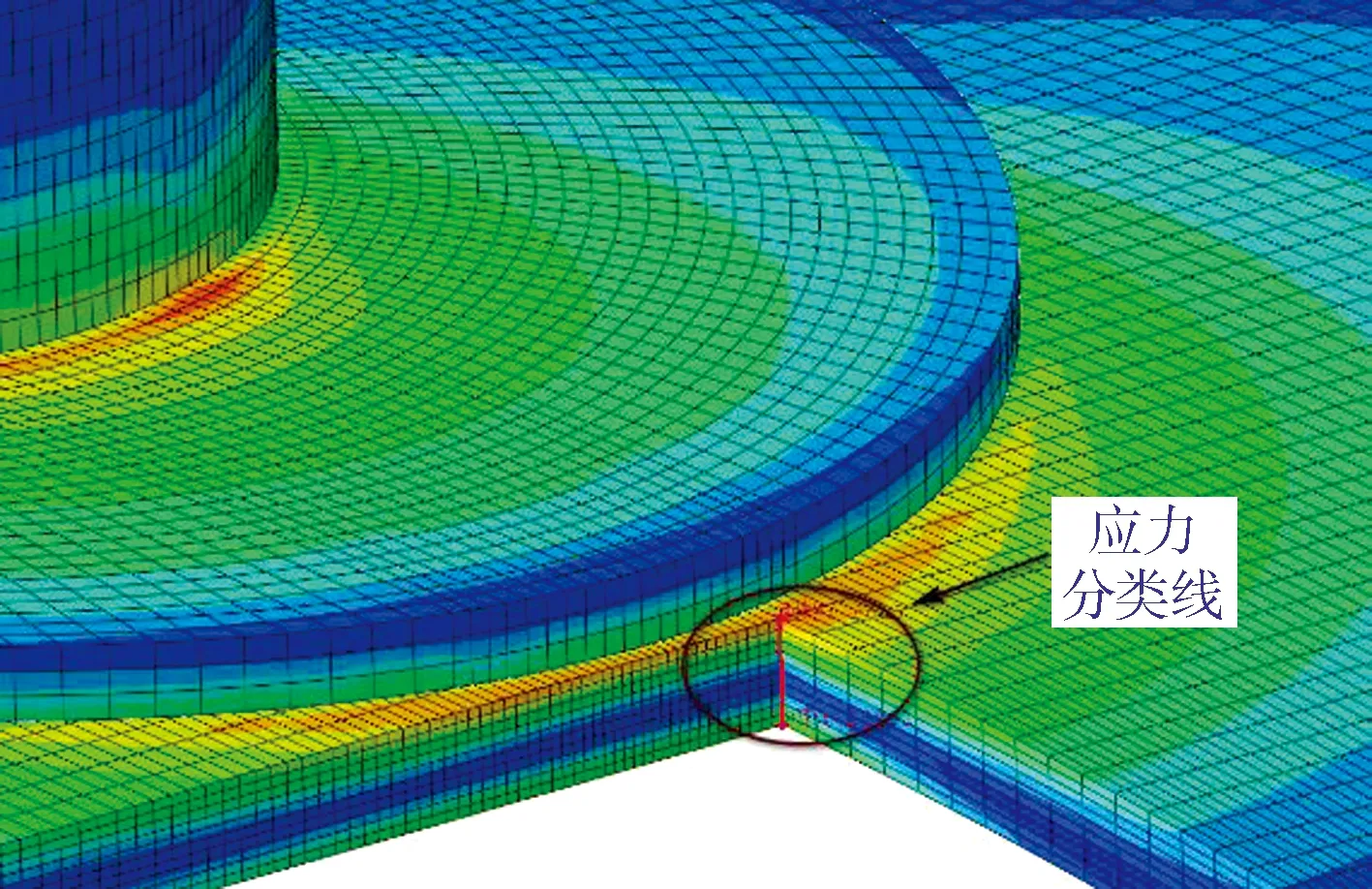
图6 应力分类线布置

提取应力分类线上所有节点的6个应力分量，如图7所示。x、y、z方向如图5所示。由图7 可以看出，各应力分量下筒体表面应力均较大，内部应力较小。因此，后续分析将重点关注筒壁表面应力。

图7 SCL上各节点的应力分量

根据应力线性化方法，对各应力分量进行计算，得到各分量的薄膜应力和表面应力，结果如图8 所示。

图8 不同应力分量下的薄膜应力及表面应力

通过求解应力张量的特征方程可以进一步得到σ1、σ2和σ3。特征方程如式(9)所示。

σ3-J1σ2-J2σ-J3=0

(9)

式中：σ1——大主应力,MPa；

σ2——中主应力,MPa；

σ3——小主应力,MPa。

其中

SⅡ/SⅣ=σ1-σ3;

J1=Sx+Sy+Sz;

(Sx·Sy+Sy·Sz+Sx·Sz);

J3=det(Sij)

Sij为应力空间6个分量。

根据方程的根进一步计算得到：薄膜应力SⅡ=33.3 MPa(Tresca应力)，与规范计算结果相差1.8%；表面应力SⅣ=215.1 MPa(起点)和SⅣ=132.2 MPa(终点)，表面应力取二者中较大值，即215.1 MPa，与规范计算结果相差2.13%。说明该方法的计算结果能够很好地反映吊耳起吊引起的筒体局部应力变化。

3 荷载参数对筒体局部应力的影响

第2节的计算及对比验证分析表明：有限元计算得到的设备局部应力与规范计算结果均相近，采用该方法能够对规范无法计算的板式吊耳进行局部应力分析。下面以板式吊耳APA-4【17】为例分析荷载参数对筒体局部应力的影响，其中肋板厚度为30 mm，筒体直径为4 m，筒体厚度为30 mm，有限元分析模型如图9所示。

图9 板式吊耳有限元分析模型

荷载方向示意如图10所示。首先分析荷载FL变化情况下筒体局部应力的变化，为控制变量个数，吊索张角θ、设备提升角α均取0°。荷载大小变化情况下的筒体局部应力计算分析结果如图11 所示。

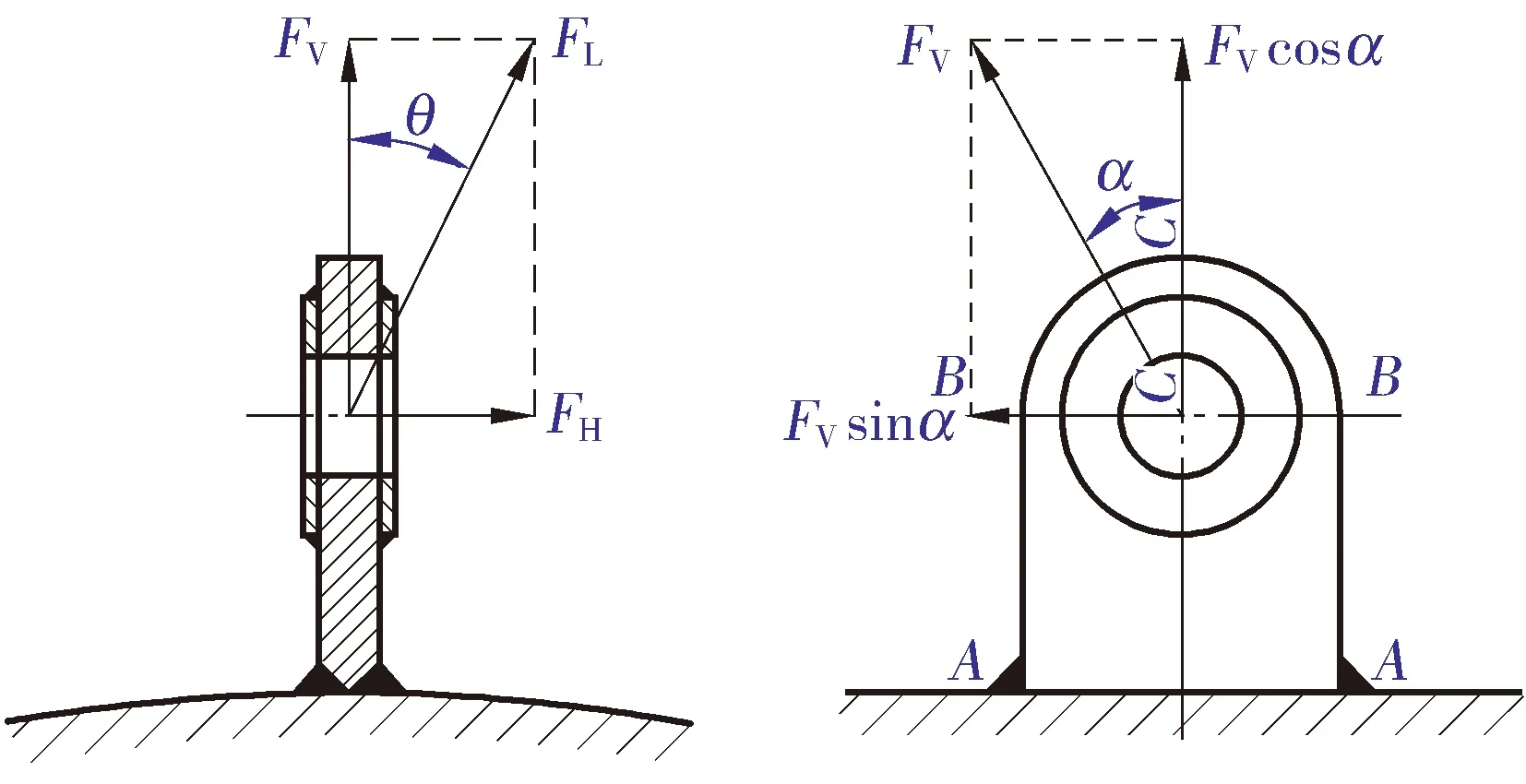
图10 板式吊耳荷载示意

图11 荷载变化对筒体局部应力的影响

由图11可以看出，荷载大小与筒体局部应力呈明显线性关系，随着荷载逐渐增加，薄膜应力SⅡ和表面应力SⅣ均逐渐增加，荷载为500 kN时，薄膜应力和表面应力分别为126 MPa和527 MPa。

进一步分析塔式设备起吊过程中，设备提升角度α变化对筒体局部应力的影响，结果如图12所示。提升角为0°，即水平状态时，荷载与筒面垂直。由图12可以看出：薄膜应力与提升角呈线性关系，提升角每增加1°，增加约1.54 MPa；表面应力与荷载呈非线性关系，随着提升角增大，表面应力逐渐增加，但增速逐渐降低。

在大型塔式设备实际起吊过程中，提升角的变化总会引起吊耳荷载大小变化，二者之间存在以下关系：

(10)

式中：T——吊耳荷载，N；

Wd——设计吊装质量，N；

L2——设备重心与顶部吊耳距离，m；

L1——顶部吊耳与尾部吊耳距离，m；

L4——吊耳孔中心与设备轴距离，m。

根据本案例计算得到的吊耳荷载与提升角关系如图13 所示。由图13可以看出，提升角在0°～80°之间时，设备提升角α与吊耳荷载T近似呈线性关系，随着提升角α继续增加，塔器尾部板式吊耳荷载急剧降低，直至为0。

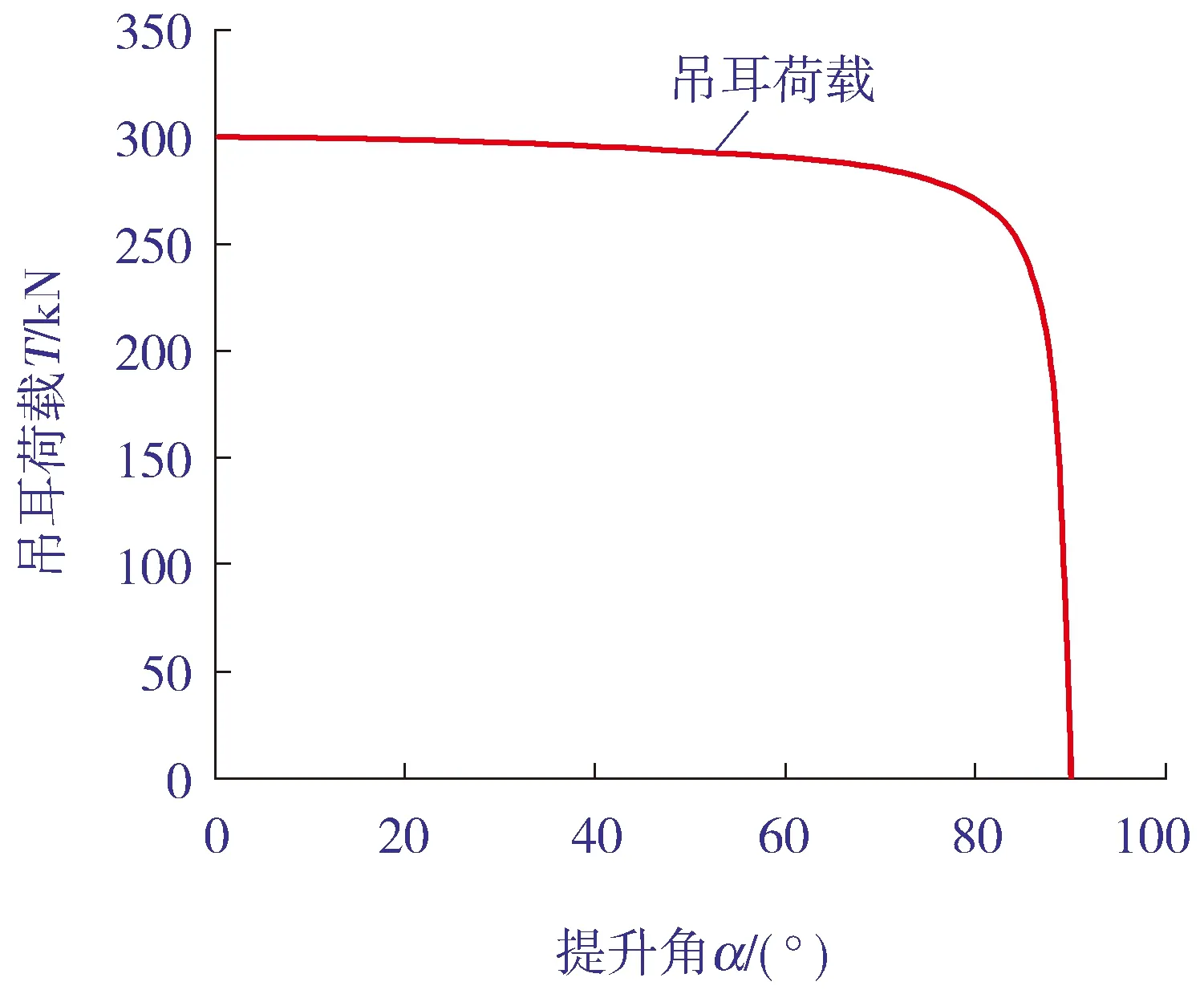
图13 吊耳荷载T与提升角α关系

再进一步分析塔器提升角α与吊耳荷载共同变化情况下筒体局部应力的变化，如图14所示。由图14 可以看出：随着提升角α逐渐增加，吊耳实际荷载发生改变，筒体局部应力先增加后迅速降低；在提升角α为60°时，局部应力达到最大值，最大薄膜应力为153.16 MPa，最大表面应力为510.18 MPa。

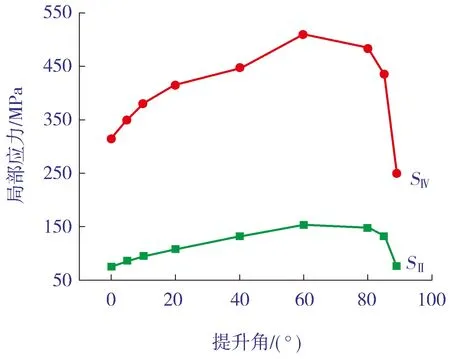
图14 提升角α与荷载共同变化情况下筒体局部应力的变化

由于设备配重不一、平衡梁倾斜等因素，吊装缆索力与吊耳在筒轴向存在夹角，故需进一步分析吊索张角θ对筒体局部应力的影响。荷载为300 kN、提升角为0°时，筒体局部应力随吊索张角θ的变化情况如图15所示。由图15可以看出：筒体局部应力受吊索张角θ影响显著，局部应力与吊索张角θ近似呈线性关系；吊索张角每增加1°，薄膜应力增加2.7 MPa，表面应力增加14.4 MPa。

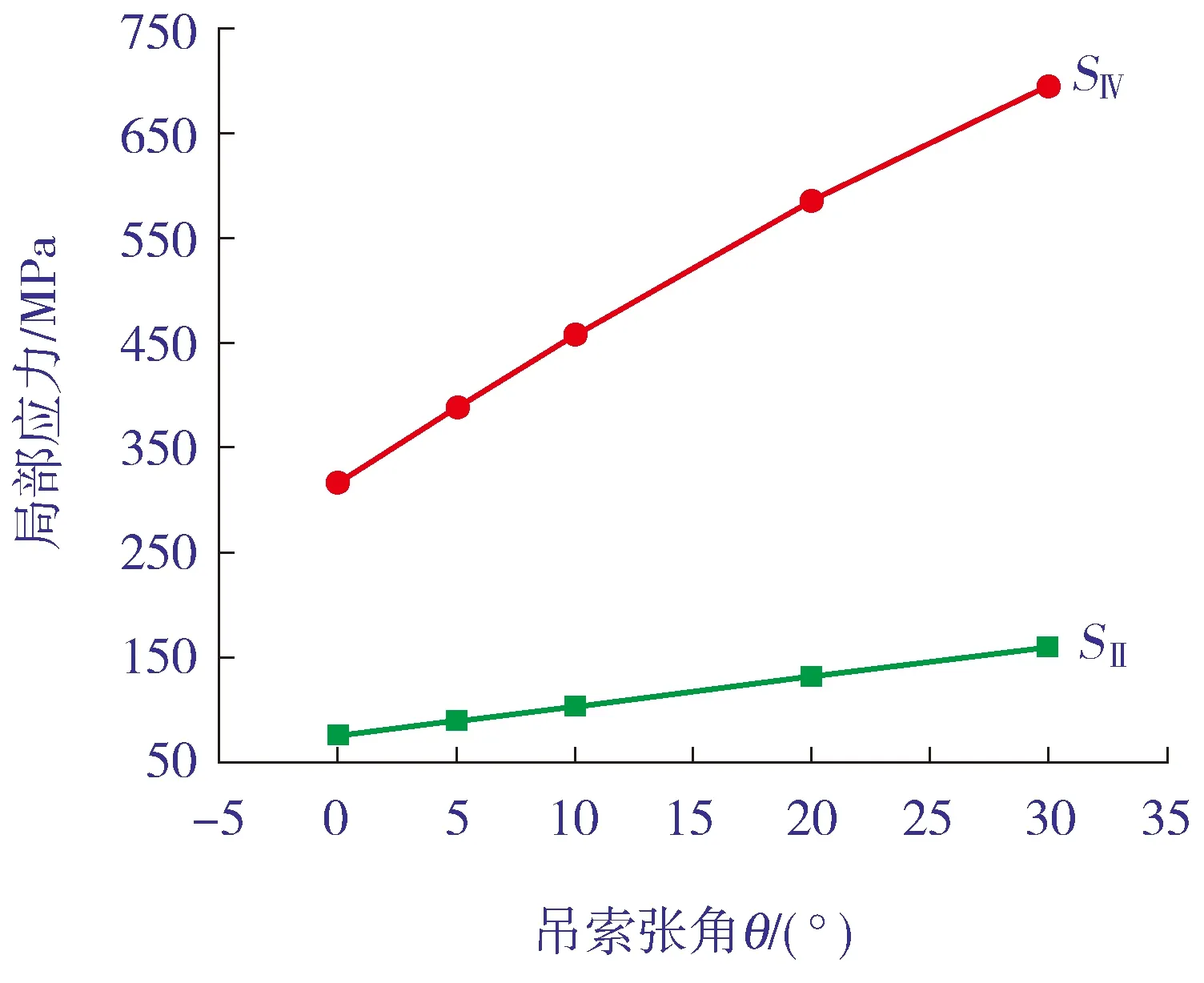
图15 吊索张角θ变化情况下筒体局部应力的变化

4 尺寸参数对筒体局部应力的影响

筒体及吊耳尺寸也是影响筒体局部应力的重要参数。本节主要分析筒体直径、筒体厚度、吊耳肋板厚度、吊耳厚度、吊耳宽度对筒体局部应力的影响，计算时荷载取300 kN，吊索张角θ、设备提升角α均取0°。筒体直径变化对局部应力的影响如图16所示。

图16 筒体直径变化对局部应力的影响

由图16可知：随着筒体直径的逐渐增加，在起吊过程中，筒体整体刚度下降，局部应力也相应的增大；薄膜应力变化幅度不大，在74～80 MPa之间，而表面应力变化明显，当筒体直径超过3 m后，直径每增加1 m，表面应力增加约18.8 MPa，需要合理设置内部支撑，保证其整体刚度。

图17所示为当筒体壁厚变化时，吊耳与筒体连接处的局部应力。由图17可以看出：筒体壁厚变化对筒体局部应力影响显著；当筒体较薄时，薄膜应力和表面应力均显著增加，壁厚为15 mm时，筒体表面应力高达900 MPa，远高于3倍许用应力限值；随着壁厚增加，筒体局部应力逐渐降低，但下降幅度逐渐变缓。

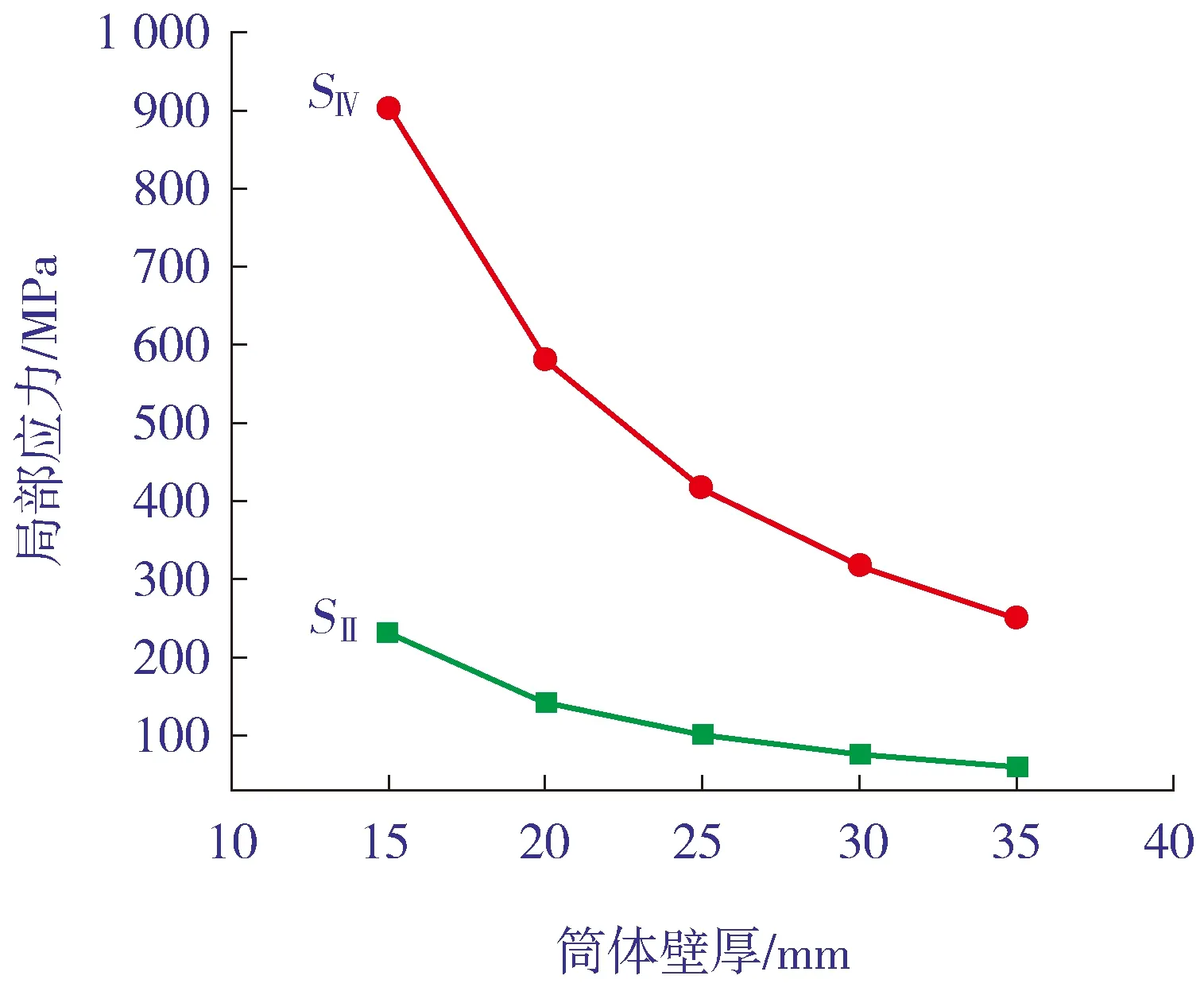
图17 筒体壁厚对局部应力的影响

为提高板式吊耳的侧向刚度和根部的焊接强度，一般在吊耳两侧增设三角形肋板。以APA-4型板式吊耳为例，分别计算肋板宽度为15、20、25、30、35和40 mm时的筒体局部应力，结果如图18 所示。由图18可以看出：增加肋板后，筒体局部应力明显降低，其中薄膜应力降低约29%，表面应力降低约10%；同时随着肋板厚度增加，筒体局部应力中，薄膜应力呈线性下降，肋板厚度每增加5 mm，薄膜应力降低1.81 MPa，表面应力呈非线性下降，速率逐渐增加。

图18 肋板宽度对局部应力的影响

进一步分析吊耳厚度和宽度变化对筒体局部应力的影响,结果分别如图19和图20所示。由图19和图20可以看出：随着吊耳厚度和宽度的逐渐增加筒体局部应力逐渐降低；对于薄膜应力而言，厚度每增加10 mm，应力降低0.6 MPa；吊耳宽度变化对筒体局部应力变化有限，宽度每增加100 mm，薄膜应力应力降低2.2 MPa，表面应力应力降低4.8 MPa。

图19 吊耳厚度对局部应力的影响

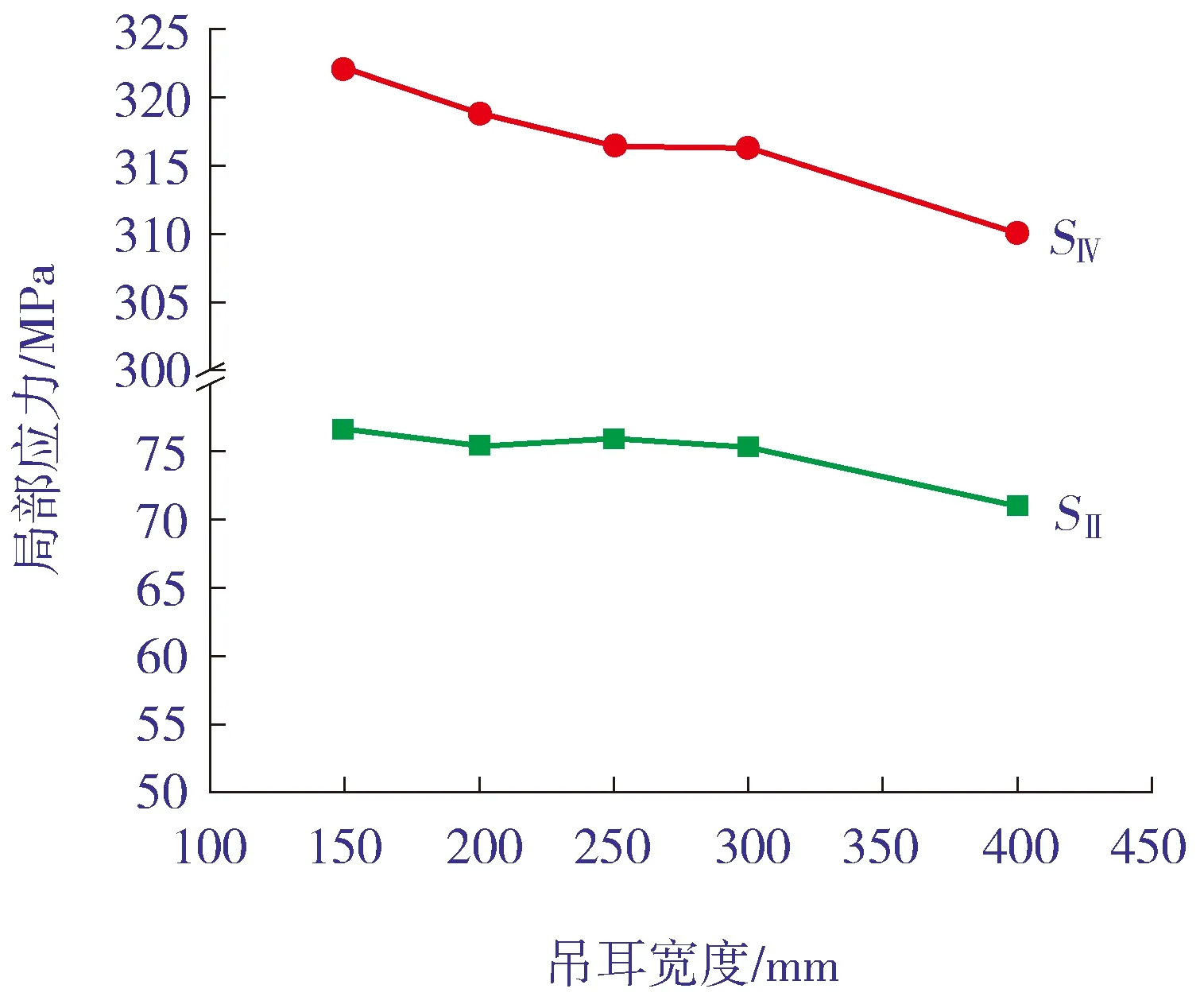
图20 吊耳宽度对局部应力的影响

5 基于正交实验的多参数因子分析

本节采用正交实验【18】对吊耳及筒体相关参数进行分析，根据实际吊耳选型及筒体参数共设置5个因素水平，以最终有限元计算得到的薄膜应力和表面应力作为实验指标，不考虑各因素之间的相互作用。得到的因素水平如表3所示。

表3 因素水平

根据因素水平，不考虑因素间的相互作用，选择正交表L25(56)，由于实验因素为5个，故1列设置为空列。按照实验需要进行有限元仿真计算并提取结果如表4所示。

表4 L25(56)正交实验

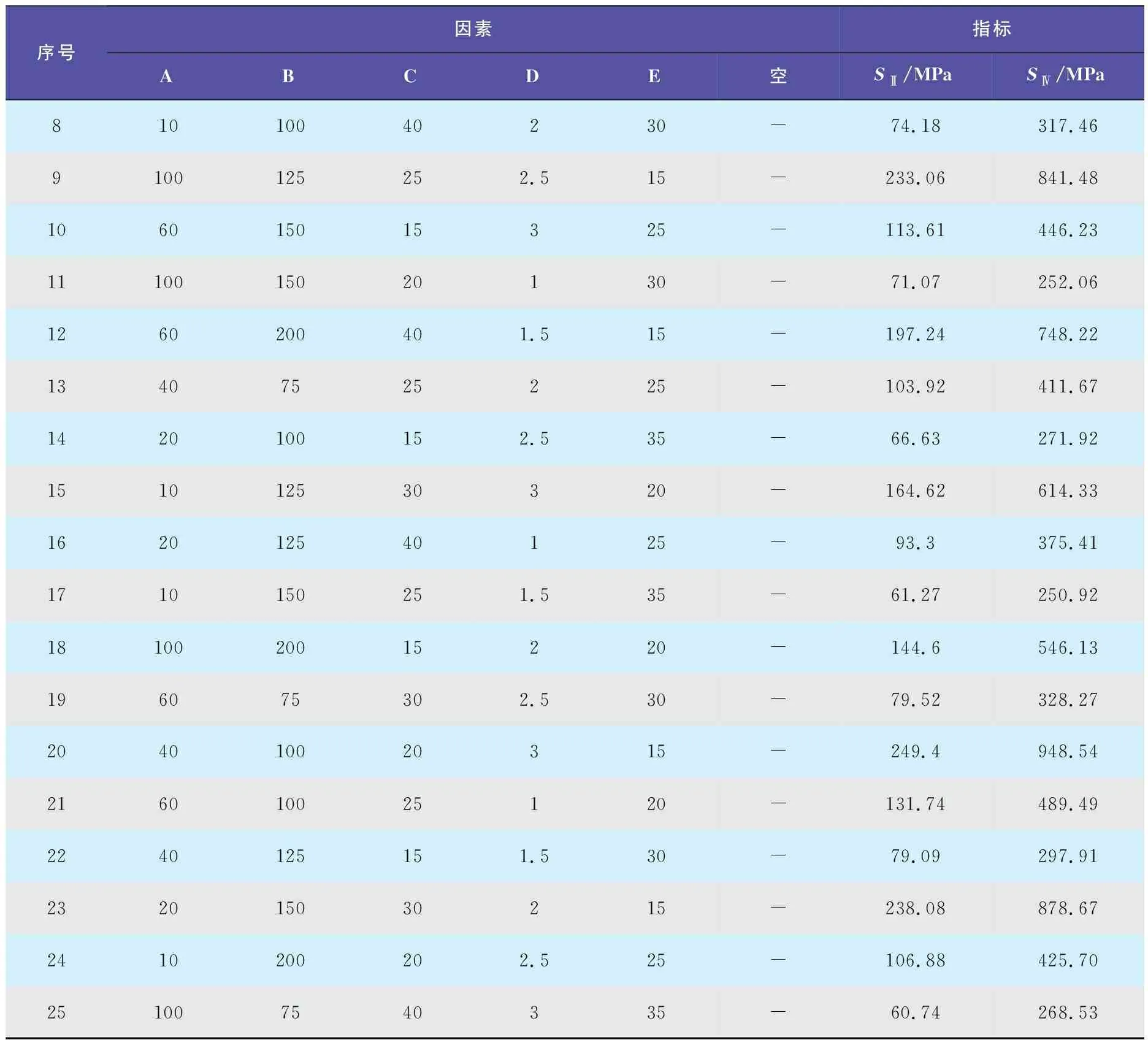
(续表4)

方差分析可以将实验指标数据总的波动分解为反映水平变化引起的波动和反映随机因数引起的波动2个部分。具体操作是将数据总的偏差平方和SST分解为反映必然性的各个因素的偏差平方和SS(SSA，SSB，…，SSE)与反映偶然性的误差偏差平方和SSe，并计算它们的平均偏差平方和MS，再由此获得各因素的均偏差平方和误差均偏差平方和的比值F。

采用SPASS计算各参数变化情况下的局部应力方差，薄膜应力方差和表面应力方差分析结果分别如表5和表6所示。

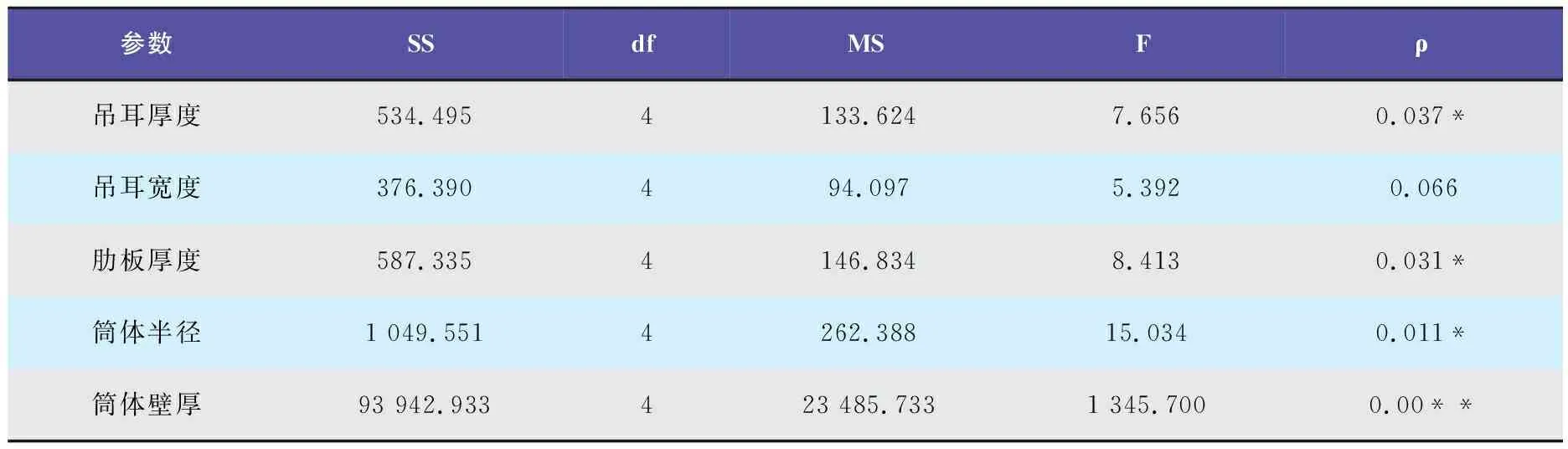
表5 薄膜应力方差分析

利用多因素方差分析研究吊耳厚度、吊耳宽度、肋板厚度、筒体半径和筒体壁厚这5项参数对于薄膜应力和表面应力的差异性影响关系，模型R2分别为0.999和0.998。由表5可知，各参数对薄膜应力的权重影响顺序为筒体壁厚、筒体半径、肋板厚度、吊耳厚度、吊耳宽度。由表6可知，各参数表面应力的权重影响顺序为筒体壁厚、筒体半径、吊耳厚度、吊耳宽度、肋板厚度。由此可以看出，吊耳宽度、肋板厚度变化对筒体局部应力不会产生明显影响。

表6 表面应力方差分析

4 结论

为分析吊装环境下塔类设备局部应力及相关参数对局部应力的影响，建立吊装环境下筒体局部应力精细化计算模型，并与规范方法相对比，主要结论如下：

1) 分析筒体局部应力时，为保证计算结果准确性，同时提高计算效率，筒体可采用半模型对称边界建模。过于简化可能导致计算结果产生较大误差。

2) 采用有限元计算吊装引起的筒体局部应力，将计算结果进行应力线性化处理，并将所得薄膜应力、表面应力与规范计算结果进行对比，结果显示，误差均在5%以内。上述结论表明，可以将有限元建模分析与规范规定相结合，指导设计与施工。

3) 荷载工况下，荷载大小与局部应力呈正线性关系，而随着提升角的增加，薄膜应力变化缓慢，表面应力则迅速增大。实际吊装过程中，提升角60°左右时，筒体局部应力达到最大值；同时筒体局部应力受吊索张角变化影响明显。

4) 通过正交实验，采用多因子方差分析方法确定了不同尺寸变化对筒体局部应力的影响权重，结果表明，筒体壁厚和半径对局部应力影响显著。吊耳宽度、肋板厚度变化对筒体局部应力不会产生明显影响。