天绘二号双星方位向天线方向图在轨测量关键技术
高敬坤,汪志龙,程家胜,丛 琳,范炜康,胡振龙
中国资源卫星应用中心,北京 100094
合成孔径雷达(synthetic aperture radar,SAR)是一种全天时全天候的对地观测手段,同时具有能反映地物电磁散射特性和图像分辨率与成像距离无关的特点[1]。干涉合成孔径雷达(interferometry synthetic aperture radar,InSAR)是SAR发展历程中的一个重要里程碑[2-9],它使得SAR具有了对三维地形的获取与重建能力,同时也是SAR遥感技术从定性走向定量的标志性进步之一。
为实现定量遥感,对星载SAR系统进行在轨定标与测试是必不可少的一环。SAR系统通过发射并接收电磁波实现对目标的探测,SAR天线正是实现电磁波收发的核心组件[10],SAR天线方向图直接影响着雷达接收机获取的地物散射回波的质量并进一步影响辐射精度、模糊度、多普勒频率、分辨率等参数[11]。另一方面,SAR天线方向图容易受到发射振动、天线展开、收发组件性能等因素的影响[12]。为实现定量SAR遥感,对天线方向图进行在轨测量具有重要意义。
自首颗SAR卫星SEASAT发射以来[13],星载SAR取得了巨大发展。绝大多数星载SAR系统特别是近20年的星载SAR系统均开展了天线方向图的在轨测量,例如SIR、ERS、RADARSAT、ENVISAT、Sentinel、TerraSAR-X、TanDEM-X以及我国的GF-3等[14-22]。为了便于对SAR天线方向图进行测量,通常将其分解为距离向天线方向图和方位向天线方向图。其中距离向天线方向图的测量方法主要包括标准角反射器法、分布目标法、地面接收机测量方法、地面发射机测量方法[23-25]等,方位向天线方向图的测量方法主要包括地面接收机测量方法和地面发射机测量方法[25-26]等。此外,由于近年来SAR系统天线波位数量的增加,上述测量方法的高人力成本和时间成本问题也更加凸显,为提高测试效率,业界还发展了外部特性因子法[27]和基于数学模型的方法[28]等,这些方法一方面极大地提高了测试效率,另一方面它们仍然以前面提到的方法为基础。
天绘二号卫星组是我国首型以双星编队绕飞方式工作的微波InSAR测绘卫星[29]。在轨测试初期,两星采用一前一后的跟飞模式飞行,并独立工作于SAR模式以便于分别对两星进行测试。对于SAR天线方向图测量,一方面,当卫星在轨完成SAR天线板展开后天线工作状态保持稳定;另一方面,方位向天线方向图的测量需要地面设备的配合从而带来较高成本。因此,SAR天线方向图特别是方位向方向图的测量通常仅在卫星在轨初期即在轨测试阶段开展。现有针对SAR卫星天线方向图在轨测量的研究均是针对单SAR卫星。对于由A、B两颗卫星构成的天绘二号卫星组,在轨测量方位向天线方向图时遇到了新问题。
首先回顾基于地面接收/发射机的针对单SAR卫星的方位向天线方向图测量方法。如图1所示,在针对单SAR卫星天线方向图的典型测量方法中,需分别测量发射方向图和接收方向图,然后将发射和接收方向图进行综合处理以获得最终的方位向SAR天线双程方向图。具体为:首先利用地面接收机采集卫星在工作期间发射的信号,并提取SAR天线的发射方向图(图1(a));然后在另一卫星飞行圈次,利用地面发射机发射特定波形的信号,通过对卫星接收到的包含地面发射机信号的SAR载荷数据进行处理,提取SAR天线的接收方向图(图1(b))。
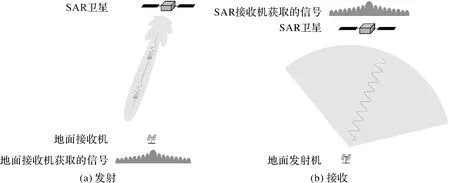
图1 单SAR卫星方位向天线方向图测量方法Fig.1 Conventional method for azimuth single-SAR antenna pattern measurement
天绘二号卫星组在轨测试期间进行方位向SAR天线发射方向图测量的示意图如图2所示。可以看出,在对前后跟飞模式下的A、B两颗卫星展开SAR天线发射方向图测量时,地面接收机中两星的信号叠在一起,从而给分别提取两颗卫星的方向图带来困难,这在以往对单颗SAR卫星的测试过程中是未遇到的。针对上述问题,本文提出了一种进行信号分离的方法,使得在前后跟飞模式下同时测量两星方向图成为可能。相比于在跟飞测试阶段对每颗卫星单独测量的方式,基于本文所提方法进行两星同时测量使测试效率提升了一倍。
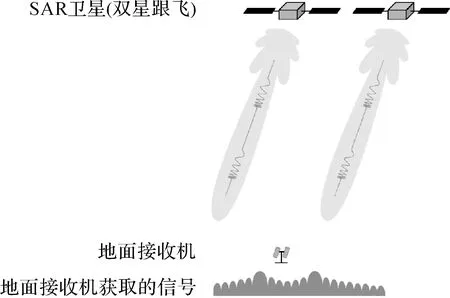
图2 天绘二号双星方位向SAR天线发射方向图测量示意Fig.2 Schematic diagram of azimuth transmitted SAR antenna pattern measurement for TH-2 satellites
1 地面接收机信号建模与分析
地面接收机对SAR卫星发射信号检波后进行采样,采集的信号可视为线性调频信号幅度包络,其信号模型可表示为
s(τ)=s1(τ)+s2(τ)+ω(τ)
(1)
式中,s1(τ)、s2(τ)分别为与卫星1、2对应的信号分量;ω(τ)为地面接收机恒定偏置和噪声。由于A星、B星为天绘二号两颗卫星的物理编号,其与地面接收机中信号分量的对应关系会随两星跟飞前后关系而变。因此为表述方便,后文将峰值在左侧的信号对应卫星记为卫星1,在右侧的为卫星2。s1(τ)、s2(τ)由式(2)给出
(2)
式中,a1[·]、a2[·]分别为对应两个卫星信号包络的幅度值;p(·)为单个单位幅度线性调频信号的包络,可认为其为宽度由发射信号脉冲宽度决定的门信号,即p(τ)=rect(τ/Tp),其中Tp为线性调频信号脉冲宽度;τ为地面接收机时间,τ=0为地面接收机采样起始时刻;t1[n1]为地面接收机接收到卫星1第n1个脉冲的时刻,t2[n2]为地面接收机接收到卫星2第n2个脉冲的时刻。设两星分别以时间间隔PRT1和PRT2发射脉冲信号,则卫星1发射第n1个脉冲的时刻和卫星2发射第n2个脉冲的时刻分别为
(3)
式中,t0,1、t0,2为常数,它们分别代表两颗卫星发射首个脉冲的起始时刻,参考0时刻为地面接收机采样起始时刻。根据卫星发射端与地面接收端时延关系可知
(4)
式中,c代表光速;R1[n1]为卫星1发射第n1个脉冲时到地面接收机的距离;R2[n2]为卫星2发射第n2个脉冲时到地面接收机的距离。
对式(4)中的R1(·)和R2(·)进行建模,需要卫星与地面接收机间的几何模型,以单颗卫星为例,几何关系如图3所示。
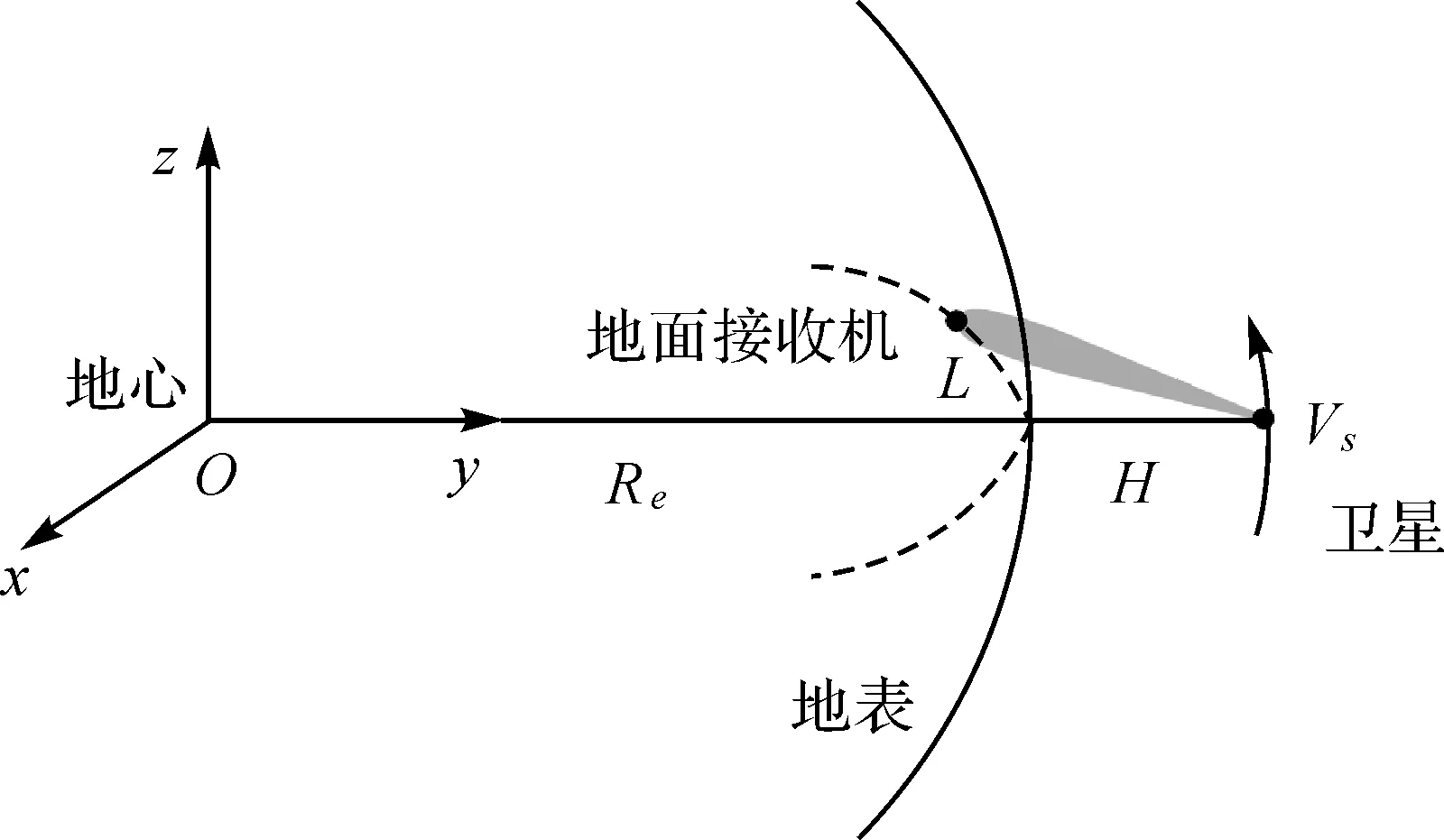
图3 卫星与地面接收机几何关系Fig.3 Geometry relationship between the satellite and the ground receiver
图3中,O-xyz为地心地固坐标系;Re为地球半径;H为卫星轨道高;L为零多普勒时刻星下点到地面接收机间的距离;Vs为卫星轨道速度。以卫星零多普勒时刻为参考定义时间变量η,于是卫星位置和地面接收机位置可分别表示为
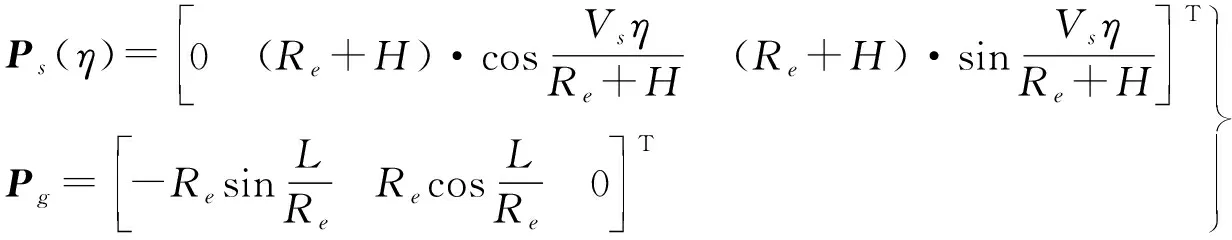
(5)
由式(5)可知,卫星-地面接收机距离可表示为R(η)=|Ps(η)-Pg|,设卫星1、2分别在各自第m1、m2个脉冲时到地面接收机距离最近,即第m1、m2个脉冲时刻分别对应两星的零多普勒时刻,于是有
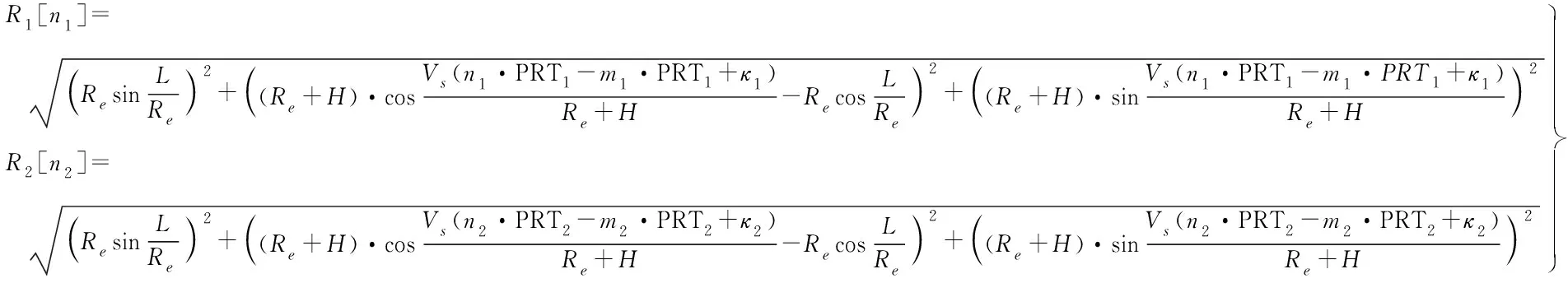
(6)
式中,κ1、κ2为对零多普勒时刻的修正量,这是由于实际情况中零多普勒时刻几乎不会恰巧等于离散的m1·PRT1或m2·PRT2时刻,后文将对各误差的影响进行专门分析。
另外,式(1)中τ为连续时间,对于地面接收机采集到的离散信号,有如下关系
τ=i/fs
(7)
式中,i为地面接收机采样点下标;fs为地面接收机信号采样率。考虑到地面接收机时钟与卫星时钟之间存在的偏差,fs会与实际标称值之间存在一个微小偏差,因此fs在上面信号模型中仍是一个待估计的未知参数。
综上,本文已建立了地面接收机同时接收两颗卫星发射信号条件下的信号模型,如式(1)—式(7)所示。进行信号分离的本质就是分别求得该信号模型中对应第1个卫星的a1[·]、t1[·]和对应第2个卫星的a2[·]、t2[·],即s(τ)分离为s1(τ)和s2(τ),后续便可分别利用s1(τ)和s2(τ)和单SAR卫星测量方法进行SAR天线方位向发射方向图的测量。
上述模型中的已知参数包括Tp、Re、H、L、Vs、PRT1、PRT2,待求解参数包括N1、N2、t0,1、t0,2、m1、m2、fs。为便于模型求解,做如下假设:①卫星1和卫星2分别在各自第m1、m2个脉冲时到地面接收机距离最近;②由于测试期间卫星二维导引已开启,因此卫星方位向波束指向与零多普勒面重合,即卫星到地面接收机距离最近时也是波束中心指向地面接收机的时刻,故而有卫星距离地面接收机距离最近时,地面接收机收到该星的发射信号幅度亦最大。以上两点假设与实际情况的偏差将带来一定的零多普勒时刻估计误差,即κ1、κ2,后文将对包含此误差的各种误差因素进行影响分析。
2 信号分离方法与分析
2.1 中间变量定义
信号分离问题现已转换为对式(1)—式(4)所示模型中未知参数的求解问题。这些未知参数与模型的代数表示十分贴近,而与地面接收机中采样的离散信号之间的关系并不直观。为了便于问题求解,现定义若干可由未知参数表示而更贴近地面接收机测量值的中间变量。分别定义卫星1第1个、第m1个、最后一个脉冲的接收时刻为
(8)
分别定义卫星2第1个、第m2个、最后一个脉冲的接收时刻为
(9)
与接收时刻对应的信号s(τ)中的离散采样下标值可分别定义如下,卫星1第1个、第m1个、最后一个脉冲接收时刻对应采样下标分别为
(10)
卫星2第1个、第m2个、最后一个脉冲接收时刻对应采样下标分别为
(11)
至此,式(10)、式(11)中的采样下标i1,1、i1,m1、i1,N1、i2,1、i2,m2、i2,N2已为可从地面接收机离散信号中直接提取的观测量。在所有待估计参数中,fs与式(10)、式(11)中直接观测量最贴近,由此可以看出对fs的标定是问题求解的关键一步。
2.2 信号分离方法
整个求解过程可分解为3个部分,分别为首-峰-尾脉冲上升沿提取、全部脉冲位置估计、脉冲幅度估计。首-峰-尾脉冲上升沿提取的作用为获得i1,1、i1,m1、i1,N1、i2,1、i2,m2、i2,N2的值。全部脉冲位置估计的作用是分别求得i1,n1、i1,n2以及对应的t1[n1]、t2[n2],其中n1=1,2,…,N1;n2=1,2,…,N2。此过程将求得模型参数N1、t0,1、m1、N2、t0,2、m2、fs。脉冲幅度估计的作用是估计与t1[n1]、t2[n2]对应的信号幅度值a1[n1]、a2[n2]。所述方法的源代码可开源获取(https:∥gitee.com/Oscargjk/azimuth-ant-beam),下面分别对上述3个部分进行介绍。
2.2.1 首-峰-尾脉冲上升沿提取
第1步:包络提取与包络滤波,包络的相邻采样点间隔约为2个脉冲重复间隔(pulse repetition time,PRT)。第2步:分别对两颗卫星对应的包络信号的峰值位置进行粗定位,粗定位精度为2个PRT。第3步:在粗定位点附近一个PRT内进行峰值脉冲上升沿检测,根据上升沿位置以及脉冲宽度确定脉冲中心位置,两颗卫星分别进行。第4步:分别对首尾脉冲进行粗定位,粗定位精度为2个PRT。第5步:在粗定位点附近一个PRT内对两颗卫星的脉冲信号进行上升沿检测,并确定脉冲中心位置,接收机信号首部和尾部分别进行。
根据上面的脉冲位置(采样点下标)确定方法,仅能给出6个下标位置,但尚不足以完全确定这6个脉冲与卫星的对应关系,特别是首尾脉冲与卫星1、2的对应关系仍有待确定。即目前已根据信号峰值位置得到i1,m1、i2,m2的值,而ik,1、i3-k,1、il,N1、i3-l,N2中的卫星标示k、l仍不确定,其中k的可取值为1或2,l的可取值同样为1或2。确定脉冲位置与卫星对应关系的过程须与下一小节介绍的“全部脉冲位置估计”配合进行。
2.2.2 全部脉冲位置估计
在此步骤中,两星的估计过程相对独立,为方便阐述,以卫星1为例进行说明。以第m1个脉冲的接收时刻为原点,定义新的时间参考
η1[o1]=t1[n1]-t1[m1]
(12)
式中,o1=n1-m1,o1∈Ζ。
依靠η1[o1]可以屏蔽m1尚为未知量而带来的影响,于是可得第o1个脉冲对应的信号采样下标值为
j1,o1=η1[o1]·fs+i1,m1
(13)
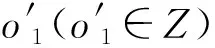
(14)
由式(14)得到标定后的fs为
(15)
由式(15)得到修正后的下标值为
(16)
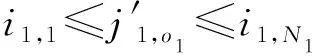
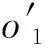
(17)
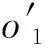
(18)
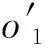
上一节中提到信号首尾下标与卫星的对应关系尚不确定,现将其确定方法简述如下:首部两个脉冲按从左至右的顺序,可分别对应卫星1、卫星2(即k=1),或者卫星2、卫星1(即k=2);尾部两个脉冲按从左至右的顺序,也可分别对应于卫星1、卫星2(即l=1),或者卫星2、卫星1(即l=2)。可见,下标与卫星的对应关系共有4种可能,分别在4种可能下求得最优的J1与J2,4种情况中J1+J2值最大者即指示了下标ik,1、i3-k,1、il,N1、i3-l,N2与卫星的正确对应关系。
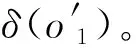
2.2.3 脉冲幅度估计
确定脉冲位置之后,最后是进行脉冲幅度估计。本文对脉冲幅度的估计区分3种情况:第1种为两星脉冲完全分离的情况,即脉冲间距大于脉冲宽度的情况;第2种为两星脉冲有部分重叠但仍可区分的情况;第3种为两星脉冲十分接近难以区分的情况。由图4(b)、(c)、(d)展示的实际采集信号看,信号幅度包络相比于理想门信号存在一定差异,实际信号幅度包络在一个脉冲宽度内可能存在一定波动。分析可知,这种不平坦可能由卫星与地面接收机相对运动带来的载频多普勒效应和卫星与地面接收机本身载频频率的微小差异导致,这种载频微小差异会造成幅度的调制衰减。因此,本文采用有效脉冲宽度内最大值来估计脉冲幅度。
对于第1种情况,将一个脉冲宽度内的采样点幅度最大值作为对该脉冲幅度值的估计;对于第2种情况,对不重叠部分的脉冲幅度取最大值作为对脉冲幅度的估计;对于第3种情况,则不定义该脉冲的幅度值。至此,已完成了由原始接收信号s(τ)分离出s1(τ)与s2(τ)的任务,后续方位向天线发射方向图的测试可依据经典的单星测量方法分别在s1(τ)和s2(τ)的基础上进行。
2.3 误差分析与适用条件分析
在本文方法中,决定信号分离精度的关键因素在于对信号s(τ)中两星脉冲时刻t1[n1]、t2[n2]估计的准确性。对于时间宽度为Tp的脉冲,若对其脉冲时刻的估计精度已达到与Tp同一量级,则很难准确捕获该脉冲,从而造成信号提取与分离的失败。
在上一小节介绍的三步分离方法中,前两步计算决定了t1[n1]、t2[n2]的值,下面分别进行分析。对于第1步计算,即脉冲上升沿提取,通过对实际信号的分析可以发现,地面接收机采集的信号s(τ)质量良好,主要表现在其具有较高的信噪比,同时每个脉冲信号的边沿陡峭完整,对上升沿的提取精度约为1个离散采样间隔。因此,脉冲上升沿估计精度主要取决于地面接收机采样率。在试验中,标称fs=1 MHz,由此得出第1步计算对t1[·]、t2[·]的估计精度约为10-6s=1 μs。
下面以卫星1为例分析第2步计算的精度。由式(6)和式(12)可知,其余脉冲时刻t1[n1]的估计是以零多普勒时刻t1[m1]为参考的,因此对t1[n1]的估计精度由式(19)的精度决定
η1[o1]=t1[n1]-t1[m1]=
(19)
简单分析可知,n1与m1偏离越大,即|o1|越大,参数误差造成η1[o1]的误差越大。再次,由于fs经过标定后与PRT1已在同一基准频率下,因此式(19)中第1项o1·PRT1的误差由标定误差决定。由式(14)可知,标定误差由第1步上升沿提取误差决定,当o1=1-m1时,其误差值约为10-6s=1 μs。
对中第2项进行误差分析,由式(15)、式(16),可以通过微分方法解析地分析(R1[n1]-R1[m1])/c与各参量间误差传递情况,参量包括Re、H、L、Vs、PRT1、κ1、c,此处省略冗长的公式。下面在典型试验条件下,给出各参量误差范围以及其对t1[n1]估计精度的影响情况。表1中假定n1与m1间对应时间长度为20 s。

表1 t1[·]估计精度分析
由以上分析可知,两步计算给t1[·]计算带来的总误差不超过5 μs,对于典型卫星脉冲宽度Tp=49 μs,5 μs误差对信号提取与分离的影响可通过设定一定冗余量而避免。上述误差分析对应代码同样已开源。
下面对算法适用条件进行分析,前文已提到本文所提方法主要解决天绘二号卫星组在轨初期即前后跟飞模式下的测试问题,在绕飞阶段不再进行SAR方位向天线方向图测量。由前述求解步骤可以看出,对两星信号峰值脉冲m1、m2的提取是后续计算的基础。由图4(a)易见,当两星间距靠近时两峰值也逐步贴近,根据信号分辨率相关理论,当第2个峰值位置与第1个峰值右侧第1零点位置重合时,无法再区分两个峰值。当两星间距小于此临界距离时,本文方法不再适用。通过实际信号测量可知峰值距第1零点时间间距约为0.55 s,在典型卫星速度Vs=7674 m/s下,两星临界距离为4.23 km。
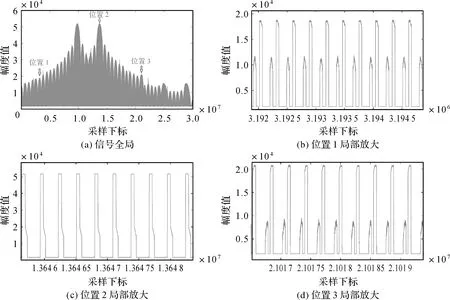
图4 天绘二号在轨测试实测地面接收机原始信号Fig.4 Collected signal in the ground receiver during the on-orbit test for TH-2 satellites
3 试验结果
下面用典型试验测试数据验证所提方法的有效性。数据的获取时间是2019年5月28日,B星先过顶,A星后过顶,A星跟随在B星后约40 km,A、B星的脉冲重复频率(pulse repetition frequency,PRF)存在微小差异,A星PRF2=3 465.904 053 Hz,B星PRF1=3 466.504 883 Hz,脉冲宽度Tp=49 μs。试验中地面接收机采样率为fs=1 MHz,地面接收机采样时长约为30 s。由以上参数可知,在地面接收机原始采样信号中,每个卫星脉冲对应的离散采样点个数约为49个。
地面接收机采样获取的原始信号如图4所示,图4展示了3个不同采样时刻附近的原始信号细节。由图4可见,两星对应的信号脉冲的相对位置关系和幅度值均在随时间发生变化。
首先进行首-峰-尾脉冲上升沿提取。下面展示包络提取与包络滤波、对两星包络信号峰值位置进行粗定位、确定两峰值处对应卫星脉冲的上升沿位置3个步骤的中间过程与结果,如图5所示。对应“首-峰-尾脉冲上升沿提取”中的第1步至第3步。
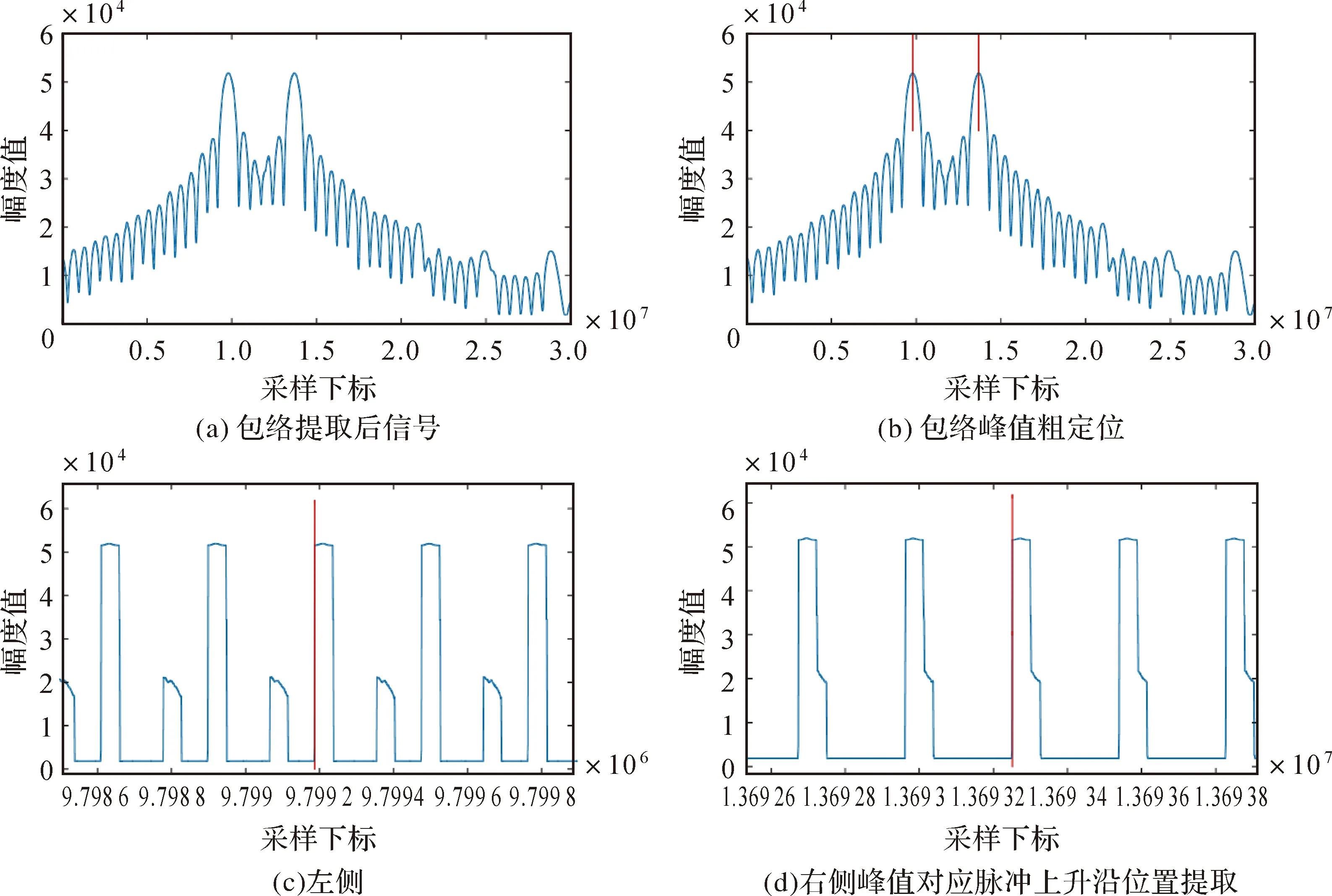
图5 两星峰值脉冲上升沿提取试验结果Fig.5 Rising edge extraction of the peak pulses
在对两星峰值脉冲进行位置提取后,已获得了直接测量量i1,m1与i2,m2的值。下面再分别对两星的首尾脉冲位置进行提取,对应首-峰-尾脉冲上升沿提取中的第4步和第5步,中间步骤与部分结果与图6所示。
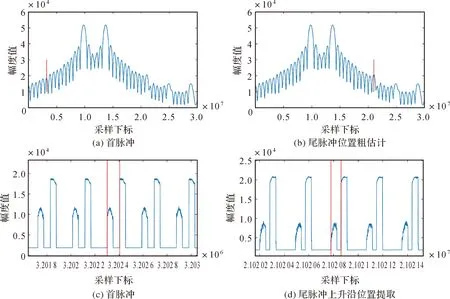
图6 两星首尾脉冲上升沿提取试验结果Fig.6 Rising edge extraction of the head and tail pulses
需要说明的是,上面所提取的两卫星对应的首尾脉冲并非是地面接收机中实际接收到的两卫星的第1个和最后一个脉冲,而是由算法确定的纳入本文第1节所建立的信号模型进行建模使用的第1个和最后一个脉冲。至此已获得了直接测量量ik,1、i3-k,1、il,N1、i3-l,N2。如第2节所分析,由于两星的脉冲相对位置关系随时间不断变化,因此仍不能确定上面4个下标位置与卫星编号的对应关系,即k、l的取值仍待定。
下面进行全部脉冲位置估计。根据第2节所提方法,使式J1+J2最大化可求得模型中位置参数并确定直接测量量ik,1、i3-k,1、il,N1、i3-l,N2与卫星的对应关系。图7展示了全部脉冲位置估计的过程与结果,其中浅蓝色线条代表地面接收机的原始观测信号,红色线条代表估计所得脉冲位置及对应的幅度值。图7(a)、(b)分别给出ik,1、i3-k,1、il,N1、i3-l,N2与卫星的对应关系不正确时的全部脉冲位置估计结果。可以看出,由于下标位置与卫星对应不正确,脉冲位置的估计出现偏差,对单颗卫星而言,仅其峰值附近的脉冲位置可以正确估计,距离峰值位置越远的脉冲位置偏差不断累积,最终导致大部分脉冲的位置无法正确估计。当脉冲位置错误时,对应位置的信号幅度值可视为地面接收机恒定偏置与噪声之和,因此对应的J1+J2较小。图7(c)、(d)展示了正确的估计结果,此时下标位置与卫星对应关系正确。由红色线条可见,正确估计位置处的信号幅度也较大,此时J1+J2取得极大值。
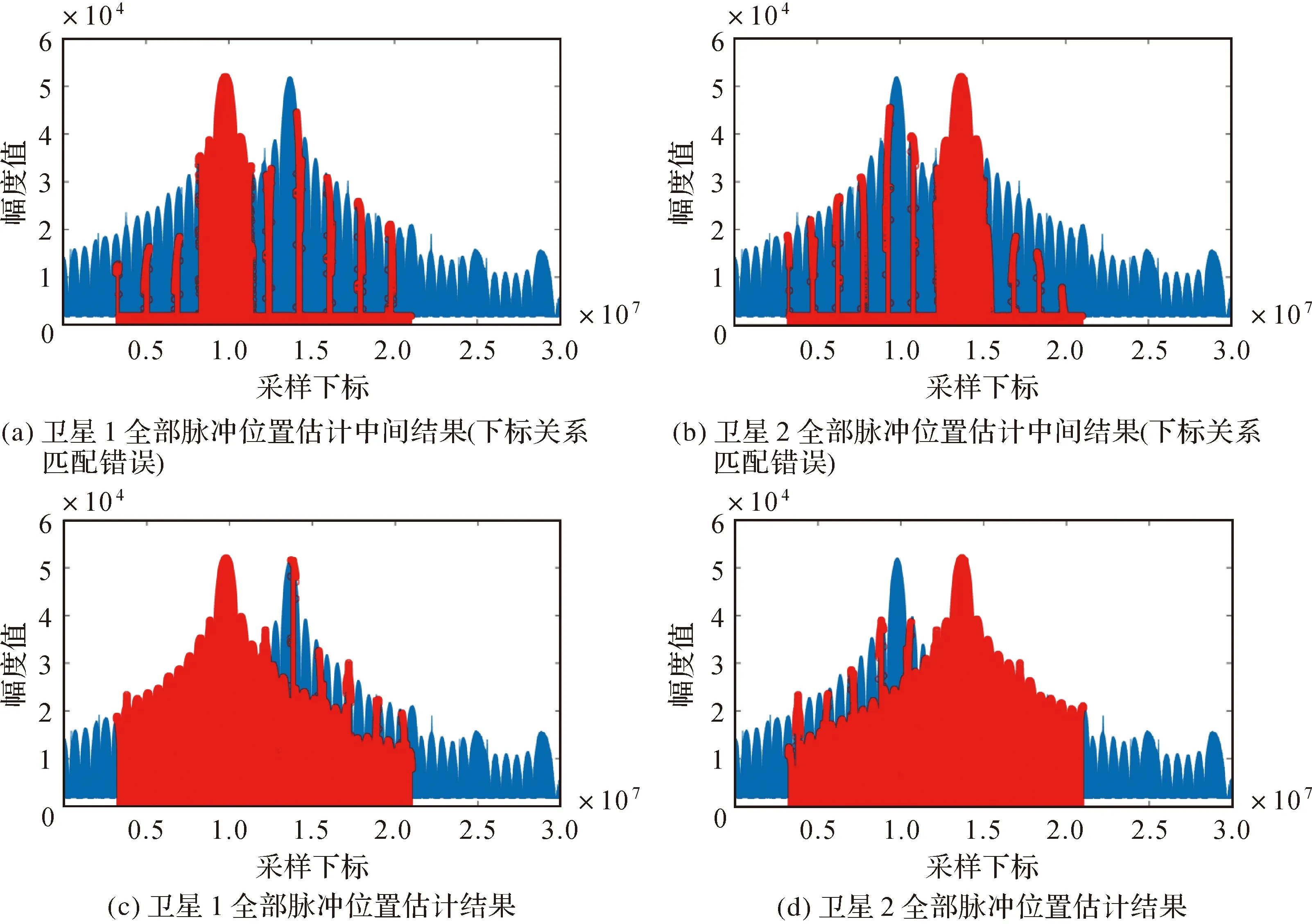
图7 两星全部脉冲位置估计过程与结果Fig.7 Results of position estimation
由图7(c)、(d)可知,虽然两星的脉冲位置得到了正确的估计,但相应位置处的信号幅度仍不能准确地反映方位向天线方向图的形状,可以发现部分红色线条对应的信号幅度值存在明显错误,这是由这些位置上两颗卫星的脉冲重叠度较高导致。为此,仍需利用第3步脉冲幅度估计进行脉冲幅度值的估计,最终可得如图8所示的估计结果。
由图8可以看出,分离出的信号中存在若干小段是无效值。这是由于两星在这些位置附近的脉冲间隔较小即重叠度很高,因而难以实现分离。在实际测试中,由于这些小段的比例较小,对指标测试并不造成障碍,若确有必要获得完整无缺的方向图信号,一种简单的方法是利用插值方法填补漏洞区域。另外,进一步分析还可得知,这些高度重叠区域或漏洞区域出现的频率正好等于两颗卫星PRF间的拍频。
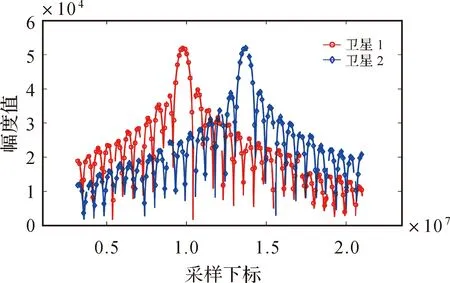
图8 幅度估计后的两星方向图分离结果Fig.8 Separation results after amplitude estimation
为了验证图8所示提取结果的准确性,将原始信号与分离结果叠在一起进行对比,分别对“首-峰-尾”脉冲位置进行局部放大,如图9所示,其中浅蓝色实现为原始观测信号,带圆形标记红色线为分离后对应卫星1的信号,带圆形标记蓝色线为分离后对应卫星2的信号。为了进一步验证信号分离的准确性,采用人工方法对分离脉冲的位置和幅度进行检查比对。对于卫星1,在“首-峰-尾”脉冲位置处,提取脉冲中心与人工读取的脉冲中心采样下标差分别为0.44、0.11、0.05;对于卫星2,在“首-峰-尾”脉冲位置处,提取脉冲中心与人工读取的脉冲中心采样下标差分别为0.54、0.01、-0.11。可见,脉冲位置提取准确性均优于1个采样点,与上一节中理论分析结果相符。在脉冲幅度方面,本文目前采用了取有效采样范围中最大值(见“脉冲幅度估计”小节)的估计方法,通过人工检查可知,所提取幅度值与有效采样范围脉内最大值相等。综上,本文所提方法能准确估计两星脉冲的位置和幅度, 所得信号分离结果为方位向SAR天线方向图后续测试开展奠定了坚实基础。
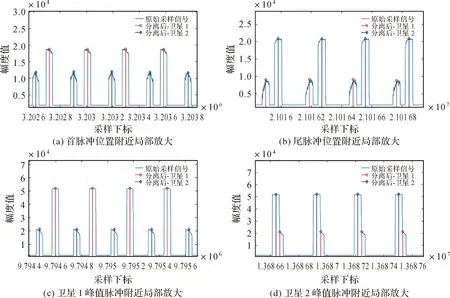
图9 原始采集信号与信号分离结果对比Fig.9 Comparison of the original collected signals and the separation results
4 结束语
针对天绘二号卫星组方位向天线方向图在轨测量期间出现的地面接收机中两星信号交叠在一起进而导致方向图测量困难的问题,本文提出了一种高效的全自动的信号分离方法。利用所提方法对信号进行分离处理后,后续测量即可按照典型的单颗SAR卫星的天线方向图测量方法进行。所提方法的基本思路是,首先进行脉冲位置估计;然后进行脉冲幅度估计,具体由首-峰-尾脉冲上升沿提取、全部脉冲位置估计、脉冲幅度估计3部分实现;最后利用试验数据展示并验证了所提方法的有效性。所提方法已成功用于天绘二号卫星的在轨测试,并保证了在轨测试的顺利进行。该方法的成功应用也为后续相似型号卫星的方位向天线方向图在轨测量提供了经验和保障。

