地铁盾构下穿立体车库修建时序的影响分析

宁德飚， 刘 婷， 郭 峰， 肖 西， 余 健

(1.云南省公路科学技术研究院， 昆明 650051； 2.昆明晟捷建筑工程技术咨询有限公司， 昆明 650214； 3.云南云岭高速公路工程咨询有限公司， 昆明 650041)

随着中国城市地铁规模的不断扩大，地铁隧道营运里程的快速增长，盾构隧道开挖工法越来越普遍。盾构机在推进、出土、拼装衬砌等自动化程度较高，在掘进效率和安全性方面有较强的优越性。由于盾构隧道开挖不可避免要穿越各种各样的地上或地下临近建筑物，如何在保证上部建筑物使用安全的条件下，保障地铁盾构隧道施工期间顺利穿过临近建筑物以及建成后运营期间不受临近建筑物的影响，对推进轨道交通建设项目的顺利实施意义重大。

土压平衡式盾构机利用刀盘切削开挖前方土体，依靠千斤顶推力克服土体压力和土体摩擦阻力向前掘进，螺旋输送机排渣的同时借助土压舱内土体压力来平衡开挖面土水压力以控制开挖面及周围土体不发生坍塌失稳。盾构机向前推进后，在其内部将预留注浆孔的管片拼装成衬砌，然后对盾尾的施工空隙实施壁后注浆，盾尾空隙产生的地层损失得以减小。

地铁盾构穿越施工时，盾构机向前掘进扰动土体，引起周边地层变形和地表沉降，进而影响附近建筑物的安全。

受隧道与建筑物的交互影响作用，二者的修建时序孰先孰后，很大程度上影响临近建筑物的正常使用及下穿地铁盾构隧道施工期与运营期的结构安全。目前国内研究隧道与临近建筑物修建时序的文献相对较少。

文献[1]利用FLAC3D对地铁区间隧道与邻近高层构筑物的不同建设时序下相互影响建立三维模型进行数值模拟分析，得出了先施工高层构筑物后施工地铁隧道的建设时序可有效避开施工风险、降低工程造价的结论。文献[2]利用Plaxis 3D将不同施工顺序引起的邻近高层建筑物结构沉降、应力重分布、塑性区分布以及倾斜情况进行数值模拟对比分析，以此对隧道穿越高层建筑物的施工顺序进行优化。

本文以地铁隧道盾构施工下穿某一拟建七层公共立体车库工程为研究背景，采用Midas GTS NX提供的数值模拟手段，分析不同修建顺序对立体车库结构与地铁隧道结构的影响，据以优化修建时序以保证地铁盾构隧道下穿立体车库时二者的结构及运营安全。

1 盾构隧道下穿施工影响计算方法

1.1 Peck理论[3]

计算盾构隧道施工的地表沉降可以采用经典Peck理论或体积损失理论。Peck理论认为地层的沉降主要是由地层损失所引起的，隧道施工沉降变形在空间上表现为随开挖不断向前推进沉降槽，沉降槽曲线为近似于一个Gauss分布曲线。Peck理论假定地层在不排水的条件下的开挖，其损失即为地表沉降槽的体积大小，如图1所示。

图1 Peck公式沉降槽

当采用Peck公式进行分析时，地表沉降横向分布的公式为

(1)

(2)

(3)

Vs=πVlR2

(4)

式中：S(x)为距离图1沉降槽O点处为x处的地表沉降，mm；Smax为O点处的地表最大沉降，mm；i为沉降槽宽度系数，m；z为盾构中心埋深；φ为土体内摩擦角；Vs为盾构单位长度的地层损失量，m3/m，也即盾构实际开挖的岩土体的体积与竣工盾构的体积之差；Vl为地层体积损失率，即单位长度地层损失占单位长度盾构体积的百分比；R为盾构机半径。

1.2 三维有限元数值模拟方法

运用地层结构法设计原理，采用三维有限元数值方法模拟盾构隧道下穿工程的施工力学行为，在实际工程中应用十分广泛。地层结构法通过建立地层、隧道、支护结构以及其他结构几何模型，赋予围岩、衬砌等物理力学参数，施加边界条件和荷载，在满足变形协调的前提下分别计算隧道管片与地层的内力和变形，分析包括施工阶段的围岩稳定、初期支护参数以及地表沉降对周围环境的影响情况等三维效应[4-8]。

有限元软件通常用荷载释放控制法或节点反力法模拟盾构隧道的开挖行为。开挖过程的模拟通过在开挖边界上施加释放荷载实现。将一个相对完整的施工阶段称为施工步，每个施工步包含若干增量步，该施工步相对应的开挖释放荷载在各个增量步中逐步释放，由释放系数控制每个增量步的荷载释放量。通过在开挖边界上设置释放荷载并将其转化为等效结点力，据以模拟开挖效应[9]。

盾构隧道开挖过程中的地层损失包含考虑了壁后注浆效应的盾构机与衬砌之间的空隙、盾构机前面的土体的弹塑性变形等。GTS NX通过设置洞周开挖土体形变至收敛位置来体现，直接在盾构隧道边缘施加强制位移边界条件来模拟应力释放过程，可以模拟任意给定的地层损失比。盾尾空隙、土体向盾尾空隙的自然充填及注浆后浆体的分布情况在GTS NX中还可以用等代层法模拟[10-11]。

盾构管片采用修正惯用法计算因管片接头存在而使管片环降低的整体刚度，用折减等效刚度ηEI(η≤1)对圆环模型进行模拟，管片错缝拼装的影响考虑用弯矩修正系数ξ(ξ≤1) 来体现，管片主截面的弯矩为(1+ξ)M,管片接头弯矩为 (1-ξ)M。根据大量管片错接头荷载试验结果，参数η取0.6～0.8,ξ取0.2～0.3[12]。

2 工程实例

2.1 项目概况

地铁盾构隧道施工项目即将下穿某一拟建七层公共立体车库工程，两个项目的修建存在工期冲突。立体车库项目场地南侧下方为规划轨道交通线，车库基底距离待建地铁盾构隧道边线最小竖向净距约为12.7 m。项目总平面布置如图2所示。

拟建立体车库建筑物占地面积为1 641.4 m2，地上建设七层车库，结构体系为钢结构框架，建成后将有335个停车位。立体车库楼层典型平面布置图如图3所示。

地铁区间隧道长为1 467.2 m，均采用盾构法施工，盾构机外径6.48 m，盾构管片外径6.2 m，内径5.5 m，厚度350 mm，管片环宽1.2 m，分块数为6块，衬砌环纵、环缝采用环螺栓连接。盾构管片断面如图4所示。

2.2 地层物理力学参数

场地范围内自上而下可分为第四系人工填土层(Q4ml)，第四系全新统冲洪积层(Q4al+pl)及第四系上更新统冲湖积层(Q3al+l)3个地层单元，岩土层从上往下分布为①杂填土、②红黏土、③红黏土、④红黏土、⑤强风化玄武岩，各土层的岩土物理力学指标取值见表1。

2.3 技术路线

本文需要研究车库与地铁的修建时序影响：一是地铁施工对先期修建的车库结构的影响，二是后期施工车库及其车辆活载变化对地铁安全的影响范围等。

第一种情形：在车库先期存在的情况下，盾构施工导致地层应力释放，地层土体产生相应的弹塑性变形，容易导致相邻车库结构物发生沉降、倾斜等现象，从而对车库结构物产生不利影响。严重时甚至危及车库结构的安全，进而影响隧道施工的安全和进度。

图2 项目总平面布置

图3 立体车库平面

图4 盾构管片断面图

表1 各土层物理力学指标

第二种情形：在地铁先期存在的情况下，车库基坑开挖和筏基回筑施工，改变了原土壤应力场的平衡，产生的土压力差容易导致相邻地铁车站结构物沿纵向和横向发生不均匀变形，从而对地铁车站结构物产生不利影响。车库建成后，进一步需考虑按设计楼面活载进行运营是否可能影响地铁结构的安全。

第三种情形：隧道和车库均已建成后，考虑按设计楼面活载进行运营对地铁结构的安全影响。

为此，本研究对上述情形采用数值模拟手段，考虑各种施工条件，对各主要施工工况进行具体的数值模拟计算，研究整个过程中车库结构或地铁结构的内力、变形情况，找出施工过程中可能对结构造成不利影响的工况进行安全性评估，提出针对性的预防措施和建议[13]。

2.4 安全评估控制值

1)车库项目为采用混凝土筏形基础，尺寸为48.4 m×38.4 m，建筑物高度为24.7 m。为确保结构安全，根据规范推荐值结合以往经验和相关理论分析，采用+10 mm和-30 mm作为建筑物结构竖向附加变形(位移)控制值，水平方向附加变形(位移)的理论控制值采用±20 mm，结构最大不同点差异沉降引起的基础倾斜控制值为12 mm[14-16]。

2)盾构隧道结构采用±10 mm作为竖向附加变形(位移)或水平方向附加变形(位移)的安全评估控制标准值。管片内力由最大裂缝宽度控制，盾构隧道结构按荷载标准组合或准永久组合并考虑长期作用影响的最大裂缝宽度迎水面按0.2 mm、背水面按0.3 mm控制。在模拟计算时将根据管片类型核查盾构内力的是否满足设计控制弯矩值，本例相应的设计控制弯矩值为137 kN·m。结合以往类似工程相关经验，如果能够控制外部项目对盾构隧道结构的附加变形在上述变形控制值内时，地铁盾构隧道的内力值变化较小，所以一般以变形控制为主[17-20]。

2.5 数值模拟计算

2.5.1 三维有限元模型

采用Midas GTS NX有限元软件建立的项目总体模型如图5所示。

图5 项目总体模型

2.5.2 盾构施工对先期修建的车库结构的影响

图6 车库建筑的水平、竖向位移

考虑车库先期修建完工的情况下，将地铁分为1、2、3段施工范围，其中进入车库建筑物之前的为1施工段，下穿车库建筑物范围为2施工段，穿过车库建筑物之后为3施工段，按每段6 m进行细分，左线分为8段，右线分为10段。

上述情形的计算结果表明，地铁盾构穿过项目建筑物的全过程，车库建筑的结构水平方向最大位移发生在y方向，其值为-3.44 mm，竖向z方向最大位移为-7.48 mm，均小于前文提出的结构位移控制限值，如图6所示。

2.5.3 车库施工对先期修建的盾构隧道的影响

项目计算范围和前述一致，考虑地铁盾构隧道先期修建完工的情况下，计算车库从开挖筏形基础到逐层施工至顶层过程的受力情况。

上述情形的计算结果表明，车库从开挖筏形基础到顶层施工完成的全过程，地铁隧道水平方向最大位移发生在y方向，其值为-4.47 mm，小于前述安全评估控制标准值；竖向z方向最大位移为-13.81 mm，已大于安全评估控制标准值，如图7所示。地铁管片弯矩Mxx最大为-154.8(kN·m)/m，Myy最大为141.9(kN·m)/m，已大于设计控制弯矩值，如图8所示。

图7 盾构隧道水平、竖向位移

图8 盾构隧道弯矩

2.5.4 车库设计活载对已建盾构隧道的影响

车库建成后，运营设计楼面活载为7.0 kN/m2，计算在设计活载作用下地铁结构的位移和变形情况。

计算结果表明，在车库设计楼面活载作用下，地铁隧道水平方向最大位移发生在y方向，其值为-4.07 mm，小于安全评估控制标准；竖向z方向最大位移为-12.44 mm，已大于安全评估控制标准，如图9所示。地铁管片弯矩Mxx最大为161.2(kN·m)/m，Myy最大为149.4(kN·m)/m，已大于设计控制弯矩值，如图10所示。

图9 盾构隧道水平、竖向位移

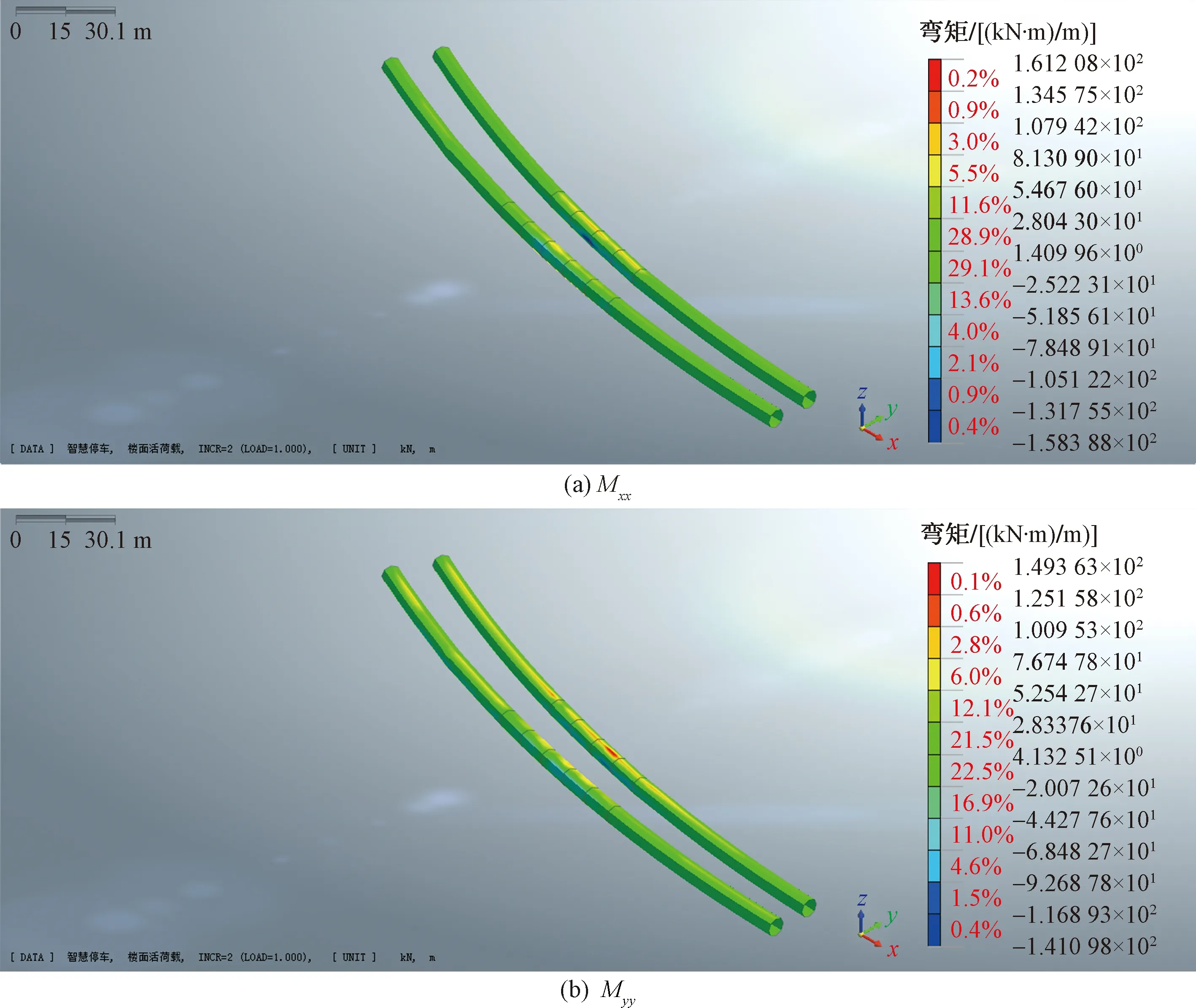
图10 盾构隧道弯矩

2.6 地铁下穿车库修建时序分析

综合以上计算结果，得到以下结论：

1)车库建筑物先期施工时，因后续地铁盾构隧道施工引起的车库建筑物位移变形附加值最大值，不超过安全评估控制标准值。

2)地铁盾构隧道先期施工时，因后续车库建筑物施工引起的隧道结构位移变形，水平方向最大位移附加值小于安全评估控制标准值；竖向z方向最大位移附加值为-13.81 mm，大于安全评估控制标准值；因后续车库建筑物施工引起的隧道结构弯矩Mxx最大值为-154.8(kN·m)/m，Myy最大值为141.9(kN·m)/m，已大于设计控制弯矩值。

3)在地铁隧道和车库建筑物均已修建完成的情况下，按设计楼面活载7.0 kN/m2作用于车库引起的地铁隧道位移变形附加值,地铁结构水平方向最大位移小于安全评估控制标准值；竖向z方向最大位移为-12.44 mm，超过了安全评估控制标准；车库按相同设计楼面活载作用时地铁结构弯矩Mxx最大为161.2(kN·m)/m，Myy最大为149.4(kN·m)/m，均已大于设计控制弯矩值。

由上述结论汇总不难看出，车库在地铁结构施工完成后再进行施工，地铁盾构管片的变形和内力均超过限值。而车库先期施工，在地铁施工抵达之前完成大部分沉降，对地铁的结构安全相对有利。同时立体车库的设计楼面活载须进行必要的调整，以满足地铁结构的安全要求。

3 结论

采用三维有限元软件对地铁盾构隧道下穿立体车库进行修建时序比较的数值模拟分析是可行的。结合不同修建时序建立工况的数值计算结果，优化二者的修建时序，有效解决了两个项目的工期冲突问题。分析成果表明，立体车库先期施工时对盾构隧道结构受力比较有利，立体车库的设计楼面活载须进行必要的调整。为同时保障地铁隧道安全掘进施工、立体车库的结构和运营安全提供了充分的决策依据。后续项目得以顺利推进直至通车运营，表明三维有限元数值仿真模拟可以为实施复杂结构项目的安全评估提供重要手段。