海口地区GPS反演大气可降水量中加权平均温度模型构建及其应用

李光伟，黄光瑞，邢峰华，敖 杰

（1.海南省气象科学研究所，海南 海口 570203；2.海南省南海气象防灾减灾重点实验室，海南 海口 570203）

引 言

强降水引起的洪涝灾害是威胁人类生存发展最严重的自然灾害之一。水汽则是大气中最活跃的成分，是强降水发生的基本条件，在辐射收支、水循环和天气气候等方面发挥关键作用，精确探测水汽具有重要意义。大气可降水量（precipitable water，PW）是指从地面直到大气顶界的单位面积大气柱中所含水汽总量，如果全部凝结并降落到地面可以产生的降水量，通常用相当的水量在单位面积容器中的深度表示，以毫米为单位，PW 可以用来表征大气中的水汽含量。PW 不能直接测量，只能通过间接方法获得。PW 计算方法主要包括探空资料计算［1］、地基全球定位系统（Global Positioning System，GPS）资料反演［2］、卫星资料反演、再分析资料计算等。传统的探空方法比较精确，缺点是探空站点和探测次数都比较少。相对于其他方法，地基GPS 反演PW 技术具有高时间分辨率和全天候的特点。地基GPS 水汽遥感资料已广泛应用于卫星和再分析水汽资料验证［3-4］、水汽日变化研究［5-6］等方面，其精度达到一定水平。BEVIS 等［2］首先提出了地基GPS 反演PW 原理，国内外许多研究对地基GPS 资料反演PW 的方法进行了详细叙述［7-11］。GPS 反演PW 过程中一个关键参数是加权平均温度（Tm），GPS 湿项延迟转换为PW 的精度主要是取决于Tm的精度。WANG 等［12］研究发现当Tm有5 K 的不确定性，可以导致PW 有1.6%～2.1%的不确定性。因此Tm模型的精度提升对PW 反演结果有重要影响。

国内外不少学者开展了地基GPS 反演PW 应用及其精度检验以及Tm本地化模型研究［7-25］。在GPS反演PW 应用及其精度检验方面，国外研究表明PW的均方根误差（root mean square error，RMSE）在北美［2，7］、欧洲［8］小于2 mm，在国际全球导航卫星系统（Global Navigation Satellite System，GNSS）服务（International GNSS Service，IGS）站点为2.6 mm［9］；在国内，有学者将利用探空等资料计算的PW 与GPS反演结果进行比较，以探空计算的PW 作为参照，GPS 反演PW 的RMSE 为5 mm 左右［11，14-16］。另外，准确计算Tm值，需要探空观测大气温湿廓线资料，但探空数据时间和空间分辨率较低。在实际应用中，Tm主要通过两种途径来得到，一是利用地面大气温度（Ts）等参量和Tm的线性或非线性关系来估计，二是利用大气模式数据或再分析资料的温湿数据采用数值积分法来计算，但模式数据或再分析资料本身具有不确定性［12］。许多学者利用基于Ts等地面观测建立了Tm模型并就其精度进行了评估，目前最广泛使用的模型是Bevis 模型（Tm=70.2+0.72Ts），该模型利用美国境内13 个探空站资料8718 个样本建立，回归Tm的RMSE 为4.74 K［2］。在国内直接应用Bevis模型会导致一定的偏差，因此许多学者对该模型进行了本地化改进［17-24］。如刘焱雄等［18］在国内较早建立了适合香港的本地Tm最优回归方程；李国翠等［21］在对Tm与地面各气象要素的关系分析基础上，建立了华北地区Tm单因子和多因子回归模型；也有利用再分析等资料估算Tm，如李建国等［17］应用MM4 中尺度模式，给出了适合中国东部地区不同季节的Tm模型。上述研究表明，Tm区域性时空特征明显，建立本地化Tm模型对提高GPS水汽反演精度有重要意义。

海南岛地处热带，干湿季分明，一年四季均有暴雨发生，水汽的精密监测是提高暴雨预报能力的关键因素。目前，关于海南岛水汽研究主要集中于利用探空、再分析等资料对海南岛PW 时空分布特征进行分析［26-28］。海南岛已建成GPS 观测网络，然而，关于海南岛GPS 反演PW 应用及其精度检验等相关研究仍比较缺乏。海南岛汛期为5—10月，为全国时间最长地区，更有必要对GPS 反演PW 精度进行分析。本文首先利用海口国家气象站2008—2010年探空数据计算Tm，并分析Tm的时间变化规律及其影响因素；然后利用2008—2012年数据建立海口地区Tm线性回归模型和加入年积日的Tm回归模型，并利用2013—2014年数据对所建模型进行统计检验；最后基于本地Tm模型对海口2012年5—10月GPS 观测数据进行PW 反演并对其精度进行检验验证。以期为本地区GPS 水汽应用及天气预报预警提供参考。

1 资料和方法

1.1 资 料

本文选取同时具有探空和地基GPS 观测，且气候上具有区域代表性的海口站进行分析，同时选取北京和武汉站进行对比分析，所用探空、地面资料和GPS 观测资料时段分别为2008年1月至2014年12月和2012年5—10月。计算Tm的探空数据是美国国家气候数据中心（National Climatic Data Center，NCDC）提供的全球站点无线电探空资料数据集（the Integrated Global Radiosonde Archive，IGRA）［29］。探空资料包括海口、北京和武汉3 站每日00：00 和12：00（世界时，下同）观测的大气垂直方向的气温、露点温度、位势高度、大气压强、风向和风速；海口地基GPS 观测资料由海口市气象局提供，GPS 资料时间分辨率为0.5 h；地面资料包括地面气压、水气压、相对湿度、露点温度、地面温度。

1.2 方 法

1.2.1 探空资料计算PW

PW 可通过利用探空获取的从地面到高空各等压面层的温度、露点温度、气压数据来计算各层饱和水汽压，进而计算各层水汽混合比，并通过水汽混合比叠加求和得到［1，12，26］。在计算PW 时，只有当地面及以上规定层至500 hPa 的压强、温度及温度露点差均有探测数据，且至少有5个标准气压层时，才进行PW值计算，否则记作缺测［12］。

国外有学者研究指出，探空仪在探测近饱和大气时，湿度观测值会出现偏低现象［30-31］。国内郝民等［32］发现中国L波段探空观测湿度也同样存在偏低现象，特别是当背景场湿度大于60%时，偏低更加明显，并提出了适合中国L波段探空湿度观测资料偏差特点的分段函数订正方法，个例试验表明，偏差订正后，观测偏差明显减小，订正效果非常显著。郝民等［33］进一步研究表明，多种探空湿度偏差订正方案均使观测湿度偏低现象得到显著改进，特别是在500 hPa 以上改进更加明显，其中订正方案5 即分段线性函数与Vömel方案结合的偏差订正方案在个例和连续预报试验中更接近实况，且订正方案5在连续预报试验的检验评分中优于其他订正方案，该订正方案对实际应用改进效果更加突出。因此本文采用订正方案5对探空观测湿度进行订正：在400 hPa以下，利用分段线性函数订正方法，对探空观测相对湿度高于60%的值进行一定的加湿订正，在400 hPa及以上采用Vömel方案进行偏差订正［30，33］。

1.2.2 GPS反演PW原理

GPS 反演PW 的原理主要是利用天顶湿项延迟与PW 建立正比关系，通过一个转换系数求解出精确的PW［2，19］。转换系数Π是Tm的函数，公式如下：

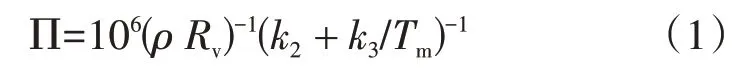
式中：ρ为液态水密度，ρ=1000 kg·m-3；Rv为水汽的气体常数，Rv=461.495 J·kg-1·K-1；k2和k3为大气物理参数，k2=22.13＋2.20 K·hPa-1，k3=3.739＋0.012 K2·hPa-1。

获取Tm的方法主要包括3 种［12，19］：常数法，探空/模式输出产品、大气再分析资料积分算法，回归经验公式。其中，常数法会导致较大的Tm误差；探空积分算法精度最高，但一天只有两次探测，站点少，时空分辨率低，对于数值预报模式输出或大气再分析产品［25］，因模式或再分析资料本身存在不确定性，限制了其应用；回归经验公式，即通过与地面气温等的关系来估算Tm，是目前最常用方法［12，19，23］，如Bevis经验公式［7］。

利用探空资料计算Tm的公式［12］如下：

式中：Pvi（hPa）、Ti（K）和zi（m）分别为第i层平均水汽压、绝对温度和高度。

在利用探空资料计算Tm时，水汽分压不能直接观测，只能利用饱和水汽压和露点温度经验关系间接获取（本文采用世界气象组织推荐的Goff-Gratch水汽压公式）。对于每日两个时次（00：00和12：00）探空观测数据，分别计算得到两个时次Tm值。

如何对Tm做回归分析、哪些因子与Tm的相关性更显著？本文采用核密度估计方法考察不同地面参数对Tm的可预报性。核密度估计是在概率论中常被用来估计未知密度函数，属于非参数检验方法［34］。简单地说，核密度估计法是一种仅从样本数据自身出发估计其概率密度函数进而准确刻画其分布特征的非参数统计方法［35］。

2 Tm与地面气象要素关系

Tm变化主要受太阳辐射影响，白天地表吸收太阳辐射能而逐渐增热，通过辐射、分子运动、湍流及对流运动和潜热输送等方式将热量传递给大气，使大气温度随之升高；夜间地表因放射长波辐射而冷却，使大气温度随之降低。因而太阳辐射和地球大气热辐射的周期变化会引起Tm的周期变化［19］。图1给出了利用探空数据计算的海口站2008—2010年Tm分别与地面气温Ts及地面气压Ps（图1）的变化。可以看出，Tm与Ps和Ts均具有明显的年周期变化，在一个年度内，Tm季节变化明显，2月为低值，7—8月为高值，且在4月存在一个次高峰，说明海口Tm年变化具有双峰结构，这与李国翠等［21］发现华北Tm具有单峰结构不同，表明华南与华北Tm年变化有明显差异。这应该与海口站地表吸收太阳辐射的季节变化有关。Tm普遍低于Ts，但两者峰值、谷值对应很好，且变化趋势和升降幅度比较一致，两者相关系数为0.776，且通过α=0.05 显著性检验。Ps高值（低值）对应Tm的低值（高值），二者增加（减少）趋势基本相反，变化幅度有一定差异。

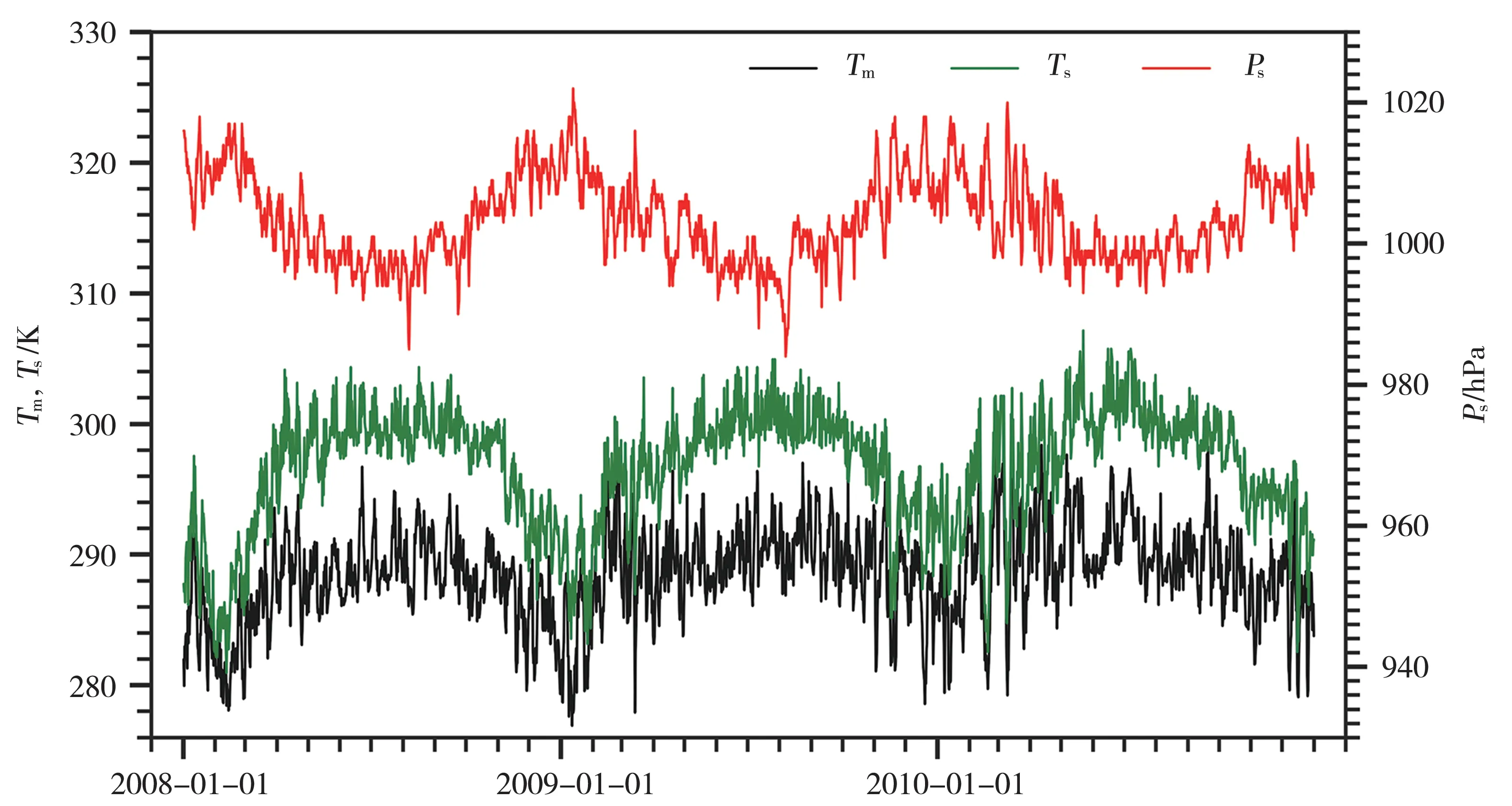
图1 2008—2010年海口站Tm与Ts及Ps时间演变Fig.1 The temporal variation of Tm and surface temperature Ts and pressure Ps at Haikou station during 2008-2010

图2给出了利用探空数据计算的海口站2008—2010年Tm分别与相对湿度RH 及地面水气压Pes的变化。可以看出，海口站Tm与RH 变化趋势和升降幅度一致性均较差。Pes与Tm变化趋势相同，Pes峰值（谷值）与Tm峰值（谷值）一一对应，但两者变化幅度略有差异。另外，Tm普遍高于地面露点温度Td，但两者峰值、谷值对应较好，变化趋势和升降幅度比较一致（图略）。

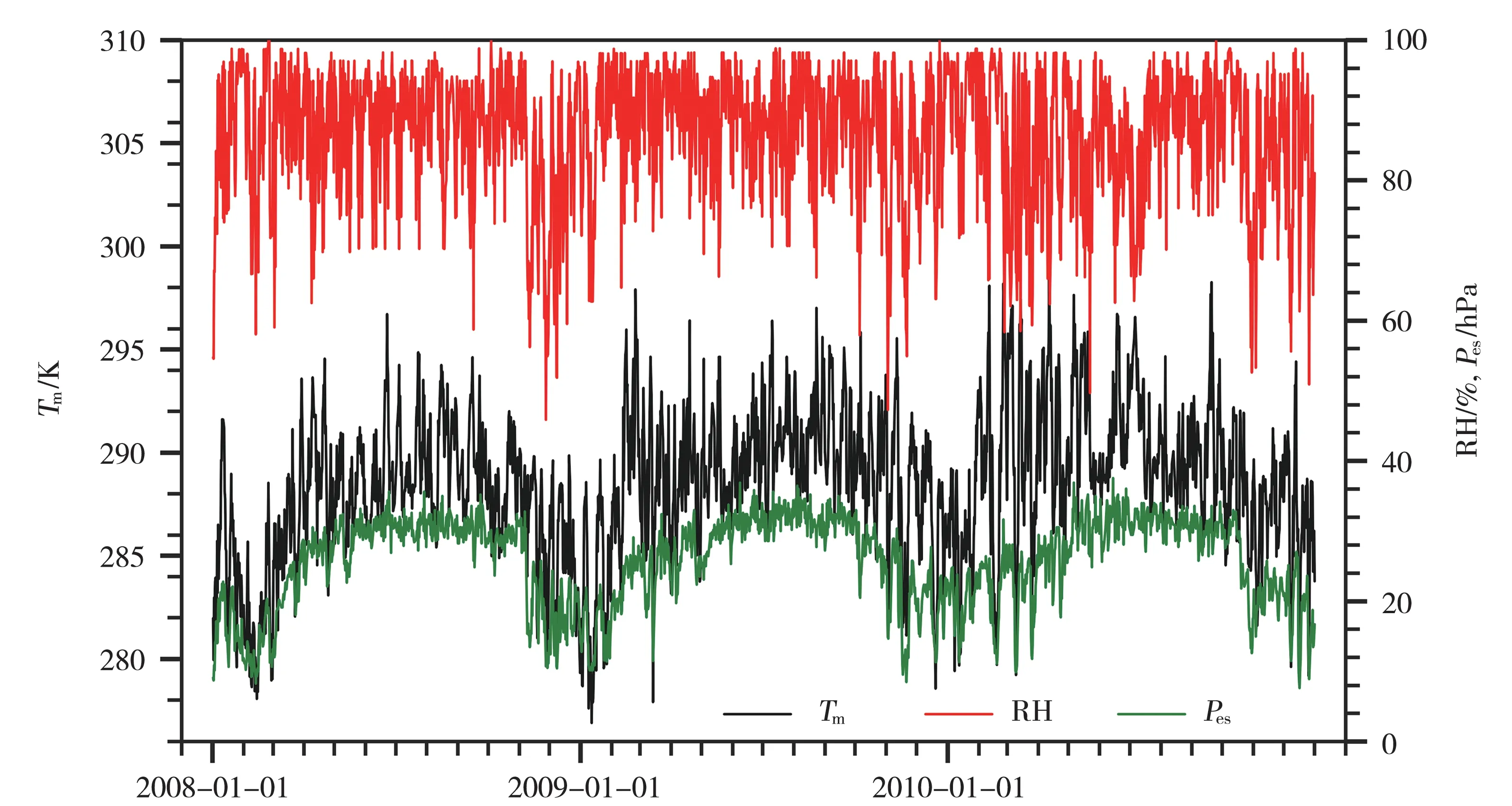
图2 2008—2010年海口站Tm与RH和Pes时间演变Fig.2 Temporal evolution of Tm and relative humidity RH and water vapor pressure Pes at Haikou station during 2008-2010

图3为海口站Tm与地面气象要素核密度估计及两者之间的散点图。可以看出，Tm与Ts和Pes散点近似成线性分布，存在较好的线性对应关系，为正相关，且Tm与Ts的概率密度曲线也比较相似，均为单峰结构；Tm与Ps则为较好的线性负相关；而同样的Tm值可以对应多个RH 值说明两者线性相关性较差。另外，Tm与地面露点温度Td呈正相关（图略）。为了理解Tm与地面温湿参量关系的南北差异，对北京站Tm与RH 等地面温湿参量的关系（图略）进行分析。与海口站类似，北京站Tm与Ts同样存在较好的线性正相关，与Ps为较好的线性负相关。但与海口站不同，北京站Tm与Ts概率密度曲线则为双峰结构。北京站Tm与Pes为非线性关系，散点呈指数分布，也与海口站不同。这说明华南和华北地区Tm与地面温湿参量的关系也存在明显不同。

图3 海口站Tm 与地面气象要素核密度估计及两者之间的散点图Fig.3 The kernel density estimation of Tm and surface meteorology element at Haikou station and scatter plots between them

3 Tm本地化模型建立

3.1 Tm常用计算方法对比

在分析Tm与各气象要素关系基础上，为对比几种常用计算Tm方法在本地的适用性，对探空积分法、Bevis经验公式和两种常数方法的计算结果进行对比（表1）分析。北京站Bevis 经验公式计算的Tm高于探空积分法，而南部地区的海口和武汉站Bevis经验公式计算的Tm则低于探空积分法。常数法计算的3站点Tm平均值相同，与探空积分法相比，偏高或偏低。

表1 2008—2010年4种常用方法计算的Tm及其他3种方法相对于探空积分法计算的Tm的RMSETab.1 Tm calculated by 4 common calculation methods and root-mean-square errors of Tm calculated by using other three methods compared with Tm calculated from radiosonde at Haikou during 2008-2010

以探空积分法计算Tm为真值，对Bevis 公式、常数法1 和常数法2 计算结果进行分析。北京、海口和武汉3 站Bevis 公式法计算Tm的均方根误差（RMSE）均小于两种常数法。以海口站为例，Bevis公式计算的Tm的RMSE 最小，为5.30 K，海口站常数法2计算的Tm的RMSE最大（18.95 K）。

图4为利用探空积分法和Bevis 公式计算得到的海口站2008—2010年Tm的时间演变，可以看出，利用Bevis 公式计算的Tm变化趋势与探空积分法计算结果比较一致，但Bevis公式计算结果在峰值区间明显较利用探空积分结果普遍偏低，说明Bevis公式计算结果能够反映海口站Tm的时间变化特征，但存在系统性偏差。

图4 探空积分法和Bevis公式计算海口站Tm时间演变Fig.4 Temporal evolution of Tm calculated by radiosonde integration method and Bevis method at Haikou station

3.2 基于地面参量的Tm单因子和多因子模型

Tm与Ts、Ps、Pes均有较好的相关性，其中与Ts相关性最高。利用海口探空站2008—2012年逐日00：00 和12：00 资料，按照四季（春季、夏季、秋季和冬季）、夏半年（5—10月）和冬半年（11月至次年4月）及全部样本，分别建立海口站Tm单因子线性回归方程，结果如表2所示。可以看出，冬、春季决定系数明显大于夏、秋季，冬半年模型决定系数则好于夏半年。

表2 2008—2012年海口站Tm分季节单因子回归模型及统计检验结果Tab.2 Tm single factor regression models considering seasonal at Haikou station during 2008-2012 and their statistical tests results

Tm分别与Ts、Td和Pes呈正相关，与Ps呈负相关性。将基于Ts、Ps、Pes、RH 及Td等5 个因子进行Tm多因子回归建模，可建立31 个回归方程，考虑到Ts与Tm的相关性最强，将不包含Ts因子的回归方程剔除后有20个回归方程。其中F1、F2、F3、F4、F5模型为单因子模型，F6、F7、F8、F9模型为两因子模型，F10、F11、F12、F13、F14、F15 模型为三因子模型，F16、F17、F18、F19 模型为四因子模型，F20 为五因子模型。进一步采用逐步回归法选择最优自变量子集筛选确定两因子、三因子等最优回归方程，结果如表3所示。

表3 2008—2012年海口站Tm单因子和多因子回归模型及统计结果Tab.3 Single-factor/multi-factor regression models of Tm at Haikou station during 2008-2012 and their statistical tests results

单因子、两因子、三因子和四因子最优回归模型分别为F1、F9、F15 和F19，其决定系数分别为0.6281、0.6339、0.6474 和0.6486，分别是单因子、两因子、三因子和四因子模型中决定系数最高的，RMSE 也是同类模型中最小。所有模型中，除F5外，其他回归模型均通过α=0.05显著性检验。由单因子模型到两因子模型决定系数有一定提升，由两因子模型到多因子模型决定系数则缓慢增加。

从因子系数看，模型的因子系数大部分均较合理，但部分多因子模型系数不合理，前述分析表明Tm与Ps为负相关，与Td呈正相关，但模型F11中Ps因子系数为正值，回归系数t统计量检验表明变量Ps对模型F11没有显著贡献。

3.3 顾及Tm周期性变化的模型优化

上述研究发现，多因子模型可以提升本地化模型的精度，但效果并不明显。根据前面的时间分析，Tm及地面气象因子均具有明显的年周期变化。因此需要针对地面气象因子模型进行周期性校正的研究。YAO 等［36］指出Tm模型误差存在周期性变化现象，并进一步通过构建补偿模型来对原模型进行改进，但并未在原模型中直接考虑这种周期性影响。臧建飞等［37］在Tm模型中对周期性残差进行考虑并进行一次建模。本文参考文献［37］做法，通过在模型中加入与年积日有关的季节校正项（a_doy）来降低Tm模型误差的周期变化，a_doy 采用了顾及年周期和半年周期的年积日三角函数表达式，公式如下：

式中：doy为年积日；a1、a2、a3和a4为拟合系数。

表4列出2008—2012年海口站加入年积日的Tm多因子回归模型及统计检验结果。可以看出，与未加入年积日的模型相比，加入年积日的Tm回归模型决定系数普遍提高，RMSE 明显减小。FD1（为F1模型中加入年积日的Tm回归模型，其他依此类推）决定系数为0.6755，相对F1 提高7.5%，比传统Bevis模型决定系数平均提升21.7%。

表4 2008—2012年海口站加入年积日的Tm多因子回归模型及统计检验结果Tab.4 Multi-factor regression models of Tm with day of year factor at Haikou station during 2008-2012 and their statistical tests results

另外，模型因子系数也存在一定改善，如模型F11 中Ps因子系数为正，FD11 模型中则变为负值。单因子和两因子模型加入年积日后，精度均提高，最优模型是FD1和FD9。三因子和四因子模型加入年积日后，最优模型分别是FD11 和FD17，均是含有Ps因子的模型，模型FD11决定系数为0.6863，相对F11提高8.3%，模型FD17 的决定系数为0.6871，相对F17提高7.9%，FD11和FD17模型计算Tm结果显示，RMSE相对未加入年积日模型也有一定程度减小。

3.4 本地化模型效果检验

利用2 a（2013—2014年）数据作为检验样本，分别对表2—4 得到的单因子模型、多因子模型（F9、F15、F19 和F20），及加入年积日的多因子非线性模型（FD1、FD9、FD11、F17 和FD20）的预报效果进行检验，检验样本同时也应用于Bevis模型（表5）。

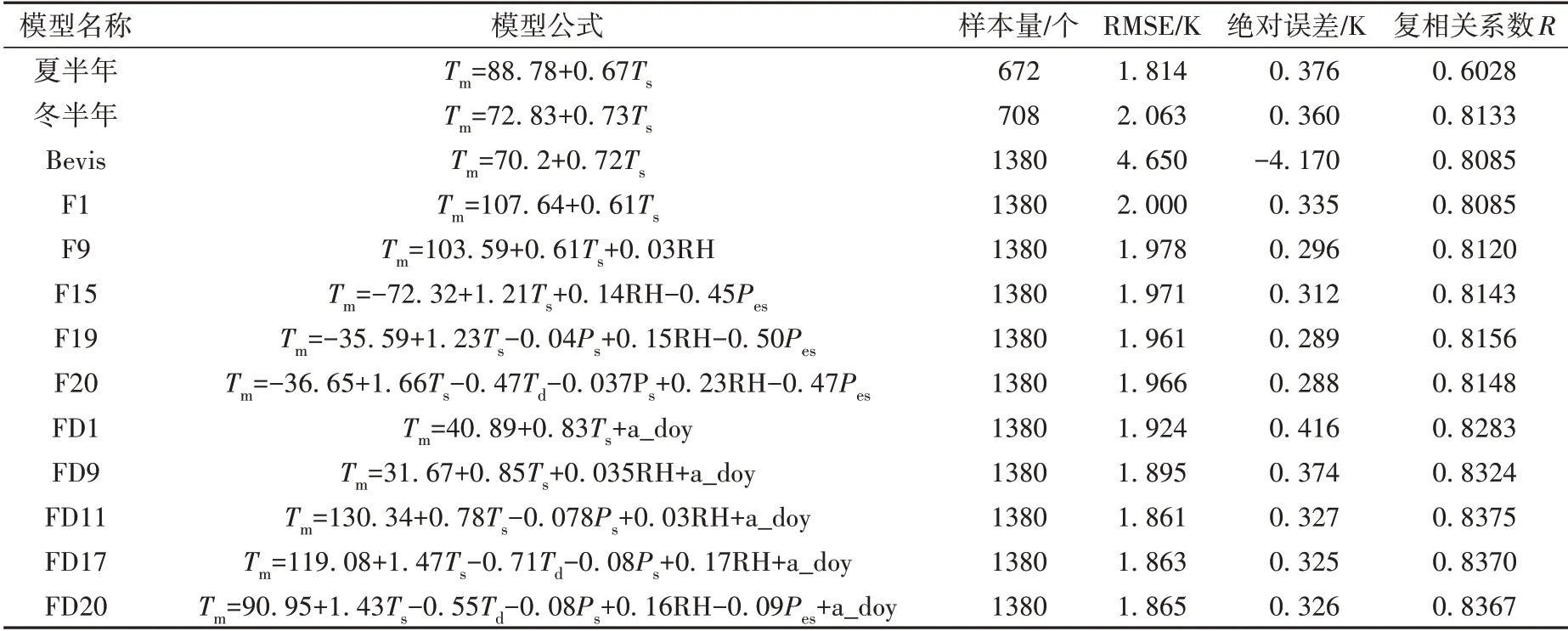
表5 2013—2014年海口站Tm回归模型统计检验结果Tab.5 Statistical tests result of Tm regression model from 2013 to 2014 at Haikou station

以探空资料计算的Tm作为真值，单因子F1模型和Bevis 模型Tm绝对误差（回归值-真值）分别为0.335 和-4.170 K，RMSE 分别为2.000 和4.650 K，说明本地单因子模型预报效果明显优于Bevis模型。加入年积日因子的FD1模型Tm绝对误差和RMSE分别为0.416 和1.924 K，预报效果也优于Bevis 模型。所有本地单因子模型中，RMSE 最小（1.814 K）的Tm模型是夏半年单因子模型，冬半年单因子模型RMSE最大（2.063 K）。

随着回归模型因子数增加，Tm的RMSE 缓慢减小，由2.000 K（F1）减小至1.865 K（FD20），模型F1、F9、F15、F19 和F20 绝对误差分别为0.335、0.296、0.312、0.289 及0.288 K，说明回归模型预报精度随因子数增加略有一定提高。模型加入年积日后模型预报精度有明显提升，如：模型FD1 和F1回归的Tm的RMSE 分别为1.924 和2.000 K，RMSE减小4%，复相关系数R（回归值与真值）分别为0.8283和0.8085。

上述分析表明，与Bevis 经验模型相比，本地单因子模型和多因子模型计算出的Tm明显接近真值，回归Tm的RMSE和绝对误差相对稳定，相对来看，本地化多因子模型的改进效果相比单因子模型略好，加入年积日的非线性多因子模型明显优于线性多因子模型。

4 Tm模型在GPS反演PW中应用

确定Tm的目的是将其应用于地基GPS 反演PW中。以2012年5—10月探空资料计算PW（PWIGRA）为参考值，与同时段GPS反演PW（PWGPS）进行对比，来评价不同Tm模型对PWGPS结果影响，表6列出基于所有分季节和F1单因子Tm模型，及预报效果较好的多因子Tm模型（FD1、F9、FD9、FD11）PWGPS与PWIGRA的结果对比。可以看出，PWGPS平均偏差绝对值在0.8 mm以内，标准差和RMSE小于5.0 mm，PWGPS与PWIGRA的相关系数均在0.9446左右，通过α=0.01显著性检验，均可较好满足实际应用需要。基于Bevis模型的PWGPS与PWIGRA的相关系数为0.9445，其标准差和RMSE 分别为4.960、4.970 mm，而基于本地夏半年Tm模型的PWGPS与PWIGRA相关系数则为0.9447，其标准差、RMSE 分别为4.900、4.913 mm。基于海口站本地夏半年等单因子和多因子Tm模型的PWGPS标准差和RMSE 均小于Bevis 模型结果，相关系数大于Bevis 模型结果。从本地Tm模型对比看，基于多因子Tm模型的PWGPS平均偏差和RMSE均小于基于单因子Tm模型，前者相关系数大于后者，PWGPS有一定提高，其中，基于加入年积日的多因子Tm模型（FD9）反演的PWGPS综合表现更好。

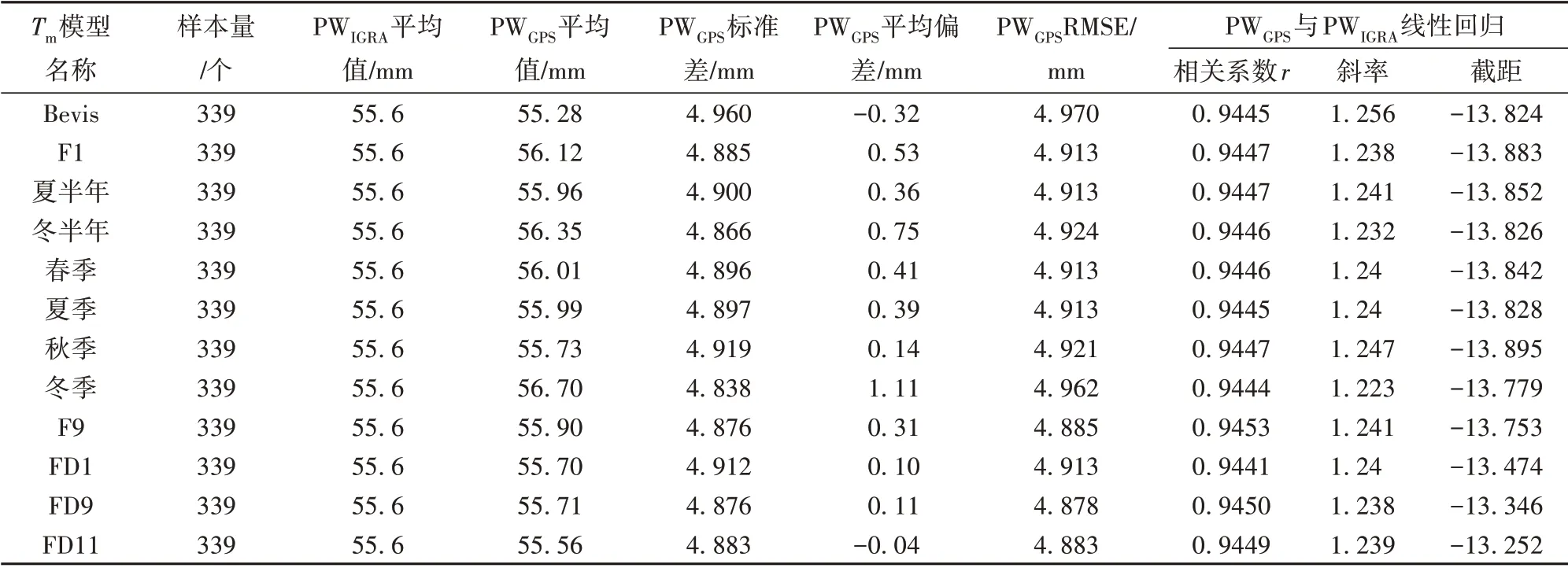
表6 海口站基于不同Tm模型的PWGPS与 PWIGRA结果对比Tab.6 Comparison of result of PWGPS based on different Tm models and PWIGRA at Haikou station

根据以上分析结果，进一步对2012年5—10月逐日00：00 和12：00 基于本地Tm模型FD9 的PWGPS及PWIGRA进行对比（图5）。可以看出，PWGPS与PWIGRA时间变化趋势比较一致，其中00：00 两者的一致性略好于12：00，7—9月两者的一致性则略好于其他月份。

图5 基于本地Tm模型FD9的PWGPS及PWIGRA2012年5—10月逐日00：00（a）和12：00（b）对比Fig.5 The comparison of daily PWGPS based on local Tm model FD9 and PWIGRA at Haikou station at 00：00 UTC （a）and 12：00 UTC （b） from May to October 2012

5 结 论

为了提高海南岛PW 反演精度和可靠性，利用海口站3 a（2008—2010年）探空和地面数据，分析了Tm变化特征及其与地面气温Ts等气象要素的关系，建立了基于地面气象要素的海口Tm单因子和多因子线性回归方程，基于5 a（2008—2012年）地面气象要素资料通过顾及Tm周期性变化（加入年积日）对模型进行了优化，并以2013—2014年探空数据计算的Tm作为参照对Tm模型进行了检验。最后进一步基于本地Tm单因子和多因子模型反演海口2012年5—10月PWGPS，并验证了新建模型的水汽反演精度。得到的主要结论如下：

（1）海口站Tm与地面气温Ts、水汽压Pes成线性正相关，与地面气压Ps呈线性负相关，与相对湿度RH的相关性不明显。

（2）利用常数法和Bevis 模型估算的海口站Tm值普遍低于探空积分法计算值，其中Bevis公式计算Tm的RMSE 明显小于常数法。利用Bevis 公式得到的Tm可随时间变化，且变化趋势与探空积分法计算结果一致，能够反映海口地区Tm的时间变化特征，而常数法则不能反映出这种变化。

（3）与利用探空积分法计算的Tm相比，本地化单因子模型F1、两因子模型F9 及Bevis 模型计算得到的海口地区Tm绝对误差分别为0.335、0.296 及-4.170 K，其RMSE分别为2.000、1.978和4.650 K，与Bevis 模型相比，两种本地化模型反演的Tm明显接近真值。

（4）多因子模型F15、F19 和F20 预报Tm结果相对于利用探空积分法计算的Tm的绝对误差分别为0.312、0.289 和0.288 K，本地化多因子线性模型随着因子增加，RMSE 缓慢减小，精度相比单因子模型略提高。加入年积日的非线性模型精度则普遍优于线性模型。

（5）不同Tm模型解算PW 与探空结果的平均偏差绝对值在0.80 mm 以内，相关系数为0.94 左右，均可较好满足实际应用需要。利用本地单因子和多因子Tm模型的GPS 反演PW 与探空值相关性更高，偏差更小，相对Bevis模型精度有一定提高，能更好反映海口地区气象条件。