1973-2020年洞庭湖水温演变特征*
潘惠敏,蔡华阳,王博芝,张 萍,姚 宇
(1:中山大学海洋工程与技术学院,河口海岸研究所,广州 510275) (2:长沙理工大学水利与环境工程学院,长沙 410114)
湖泊表层水温(即湖泊0~0.5 m或半深处的水温)是湖泊生态环境监测与评价研究领域的重要物理参数,其对气候变化和人类活动等均具有高度的敏感性[1]。湖泊水体增温直接改变湖泊热力学结构,影响湖泊热力分层和热力循环,进而影响湖泊生态系统的物理、化学和生物过程,最终引发生态系统结构和功能的重大转变[2]。例如,水温升高间接导致水体溶解氧浓度降低和营养盐载荷增加(尤其是磷),诱发水体富营养化,促进水体浮游藻类种群结构变化;改变大型水生植物的生长条件、生物量及分布;影响水体中鱼类的生存、生长发育及栖息地分布,使水生无脊椎动物种群数量减少[3]。因此,探讨湖泊表层水温在气候变化驱动下的响应过程及变化规律,对于维持区域生态环境安全具有重要意义,是湖泊热力学研究的重要科学问题。
近年来,国内外学者针对湖泊表层水温的长期演变趋势已开展一系列研究,湖泊表层水温与气温的正相关关系得到证实[4-5]。研究指出,随着气候变暖加剧,全球许多湖泊正经历一个迅速增温的过程,湖泊表层水温正在以0.3℃/10 a的速率快速上升[6-7],脆弱的湖泊生态系统将面临重大威胁。对于大多数缺乏长期水温观测的湖泊,主要采用统计学模型和确定性模型计算和预测水温[8-9]。统计学模型主要根据水温与气温等影响因子间的相关关系来预测水温。这类模型(如线性或非线性回归模型等)相对简单,对数据的需求量较少,但在统计分析中没有考虑湖泊的基本物理过程(如热分层),同时样本数据有限,不具有普适性。确定性模型主要基于水体的能量守恒及质量守恒等物理过程来模拟水温的时空演变过程。这类模型需要大量输入数据(如详实的气象数据、地貌信息、径流数据等)。由于长时序资料不足或时空分辨率不够,实际运用中往往无法满足上述数据需求条件。因此,为了克服统计学模型和确定性模型的局限性,基于物理过程的数据驱动模型被广泛应用于水温预测。这类模型的关键优势在于,将基于物理过程建立的控制方程与模型参数的统计率定相结合,同时保留统计学模型的简单性和确定性模型的鲁棒性。基于大气与湖泊表层水体的能量平衡,Piccolroaz等开发出Air2water数据驱动模型,仅以气温作为输入变量,能较为可靠地预测湖泊表层水温[10]。相比于其他统计模型和确定性模型,Air2water模型具有较高的精度,且大幅减少数据需求量[11]。
洞庭湖作为我国第二大淡水湖,在涵养水源、调蓄洪水、保育生物多样性等方面具有重要的生态服务价值[12]。长期以来,由于人类活动干扰、全球气候变化等多方面因素影响,洞庭湖生态环境持续恶化,已严重制约湖泊生态服务功能的发挥和区域的可持续性发展。目前,国内很多学者对洞庭湖已进行较为系统的研究,主要集中在长序列湖泊面积、水位和流量对气候变化的响应研究[13-15],但由于观测数据的缺乏,对湖泊水温变化及其驱动机制的研究仍有待进一步深入。综上,本文针对湖泊表层水温的长期演变趋势问题,通过收集不同站点的实测湖泊水温及相应的气象站资料,采用数据驱动模型重构洞庭湖的长序列水温,结合数理统计方法研究在气象条件驱动下湖泊表层水温的演变特征。在此基础上,初步评估气候变暖对湖泊水热平衡的影响,探讨湖泊表层水温与气温之间的耦合关系演变,以期为湖泊表层水温预测提供借鉴参考,从而为洞庭湖湖区生态环境监测、水安全保障和综合治理等提供理论依据。此外,本文提出的Air2water数据驱动模型的成功应用,将有助于揭示湖泊对气候变化的热响应过程及机制。
1 研究区域、资料与方法
1.1 研究区域概况
洞庭湖(28°30′~30°20′N,111°40′~113°10′E)位于湖南省东北部、长江中游荆江南岸(图1)。该湖泊天然湖泊总面积2625 km2,总蓄水量167亿m3,流域面积26.33万km2[16]。洞庭湖区属北亚热带湿润季风气候,具有四季分明、热量丰富、降水充沛的气候特征,年均气温在15~18℃之间,年降水量在1148~1837 mm之间[17]。洞庭湖是长江出三峡进入中下游平原后的第一个通江湖泊,是兼具蓄、泄功能的过水性洪道型湖泊。洞庭湖承纳荆江段“三口”(即松滋口、太平口、藕池口,调弦口1958年建闸封闭)分流及“四水”(湘江、资水、沅江、澧水)来水,经湖泊调蓄后由城陵矶注入长江,形成吞吐长江之势以及复杂的江河湖水系格局[18]。由于历史演变和泥沙淤积严重,湖区现可分为东洞庭湖、南洞庭湖和西洞庭湖3个不同区域,地势呈“西北高、东南低”之势。东洞庭湖面积1328 km2,约占洞庭湖面积的50%,是洞庭湖的主体湖。
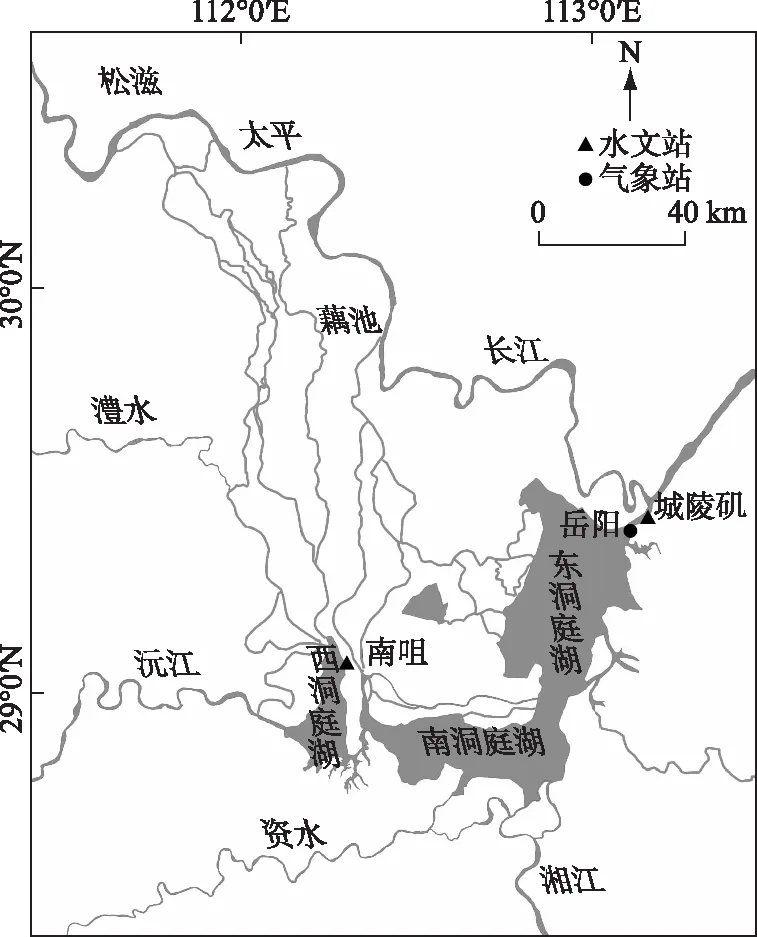
图1 洞庭湖区域及水文气象站点位置Fig.1 Geographical location of Lake Dongting displaying hydrological and meteorological stations
1.2 数据来源
本文所用水文数据为2007-2018年东洞庭湖入江口城陵矶水文站、西洞庭湖南咀水位站的实测日均水温(水面以下0.5 m深处的水温),资料来自《中华人民共和国水文年鉴第6卷长江流域水文资料:洞庭湖区》;气象数据为1973-2020年岳阳气象站的监测数据,采样时间间隔为3 h,来自美国国家气候数据中心(National Climatic Data Center,NCDC,网址:ftp://ftp.ncdc.noaa.gov/pub/data/noaa/isd-lite/)。站点位置如图1所示。为了使资料序列统一和便于统计分析,首先对原始气温数据进行预处理,将同一天内每隔3 h的气温累加求平均值,得到日均尺度的气温序列。此外,对于气温数据出现的个别缺失值,采用三次样条插值法插补,构建完整的长时间序列以保证数据的连续性。
1.3 研究方法
1.3.1 Air2water模型 本文采用Piccolroaz等开发的Air2water数据驱动模型(源代码来自https://github.com/spiccolroaz/Air2water)用于重构湖泊表层水温序列。该模型假定气温是驱动水温-气温系统演化的主要因子,是基于能量平衡的一维热力学模型,一般适用于日均时间尺度的水温预测。在实际应用中,气温是唯一的输入变量。该模型采用湖泊表层水体热量的体积积分方程来描述湖面与大气的热量交换过程[10]:
(1)
式中,ρ为湖水密度;cp为常压比热容;Vs为湖泊表层水体体积;Tw为日均水温;t为时间,一般以日为单位;Hnet为净热通量;A为湖泊表层面积。
Piccolroaz等通过对式(1)进行适当简化(具体推导过程见参考文献[10]),建立完整的8参数模型,方程如下:
(2)
(3)
式中,pi(i=1, 2, 3, 4, 5, 6, 7, 8)为模型率定参数;Tr为深水温度的参考温度,冷季对流混合型湖泊的Tr假定为最高水温,暖季对流混合型湖泊的Tr假定为最低水温,双季对流混合型湖泊的Tr假定为4℃;δ表示表层水体体积Vs与参考体积Vr的比值,为无量纲参数;tyr表示一年的时间。
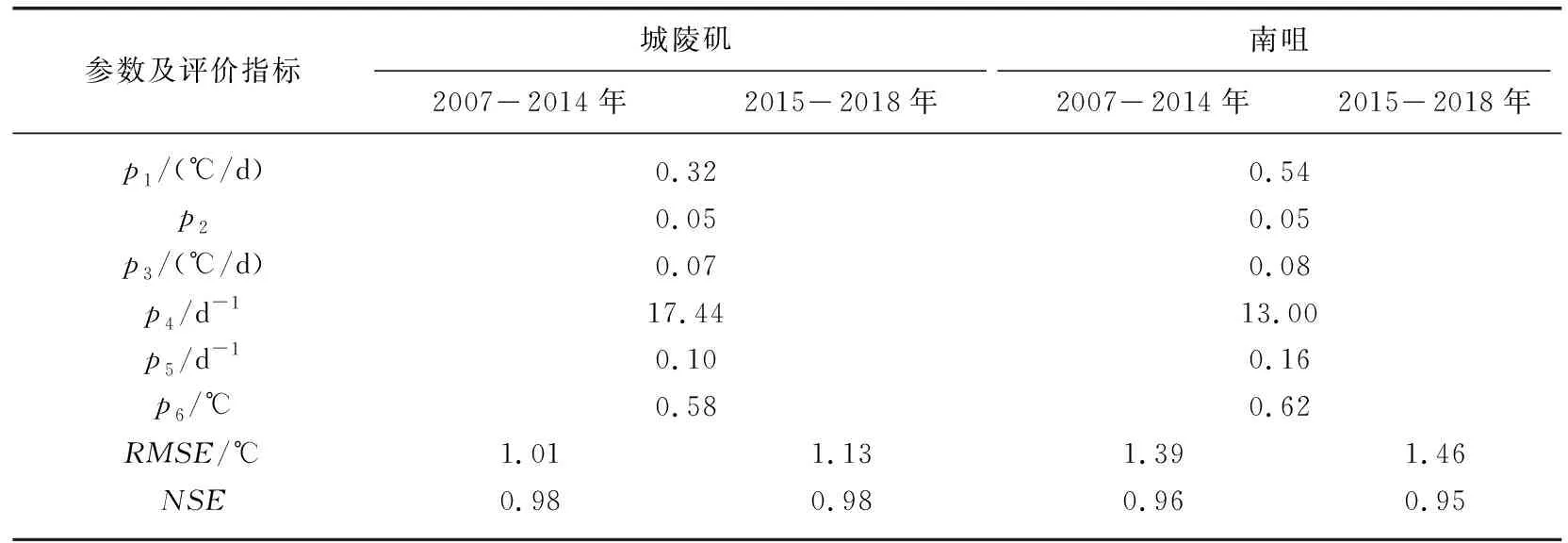
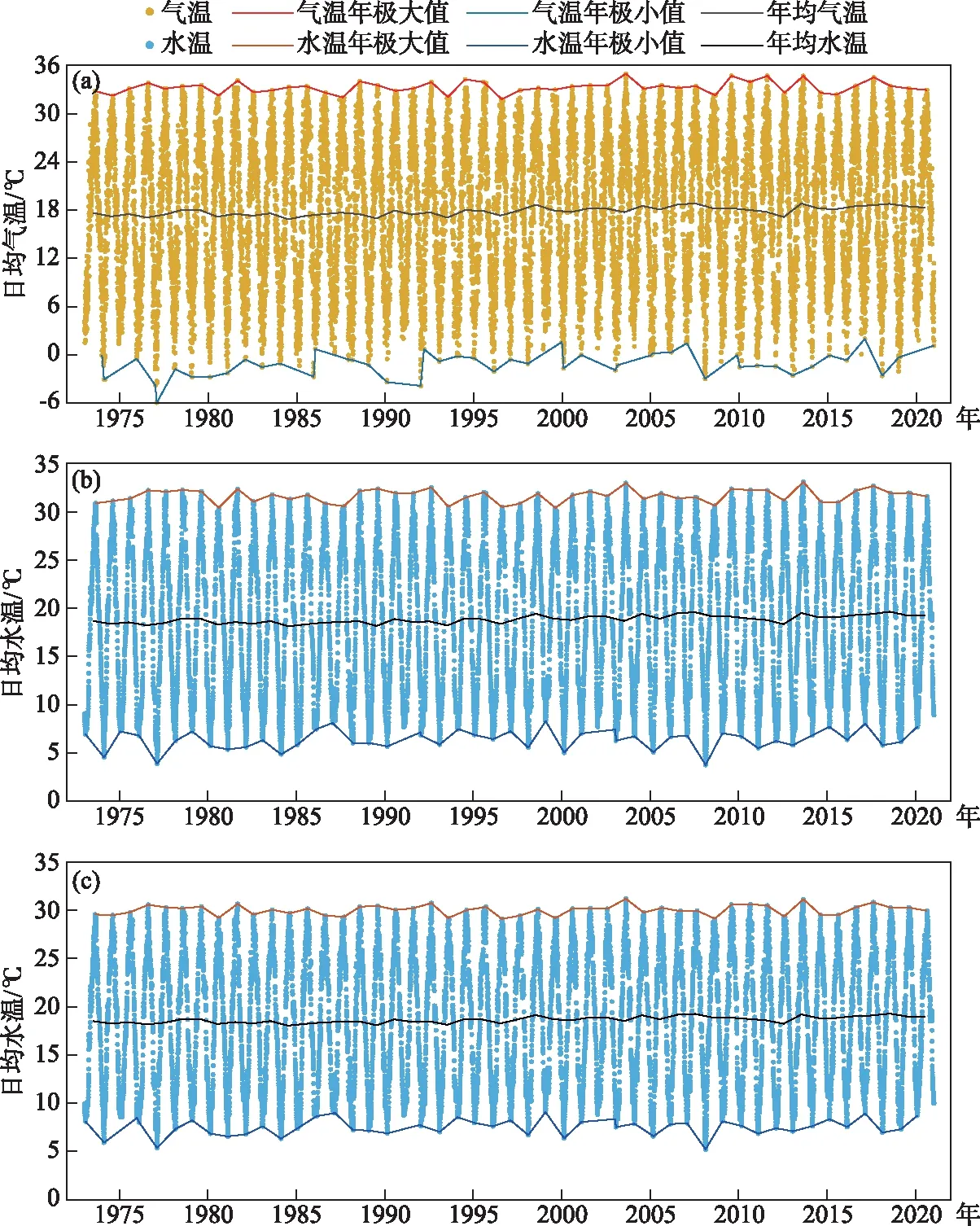
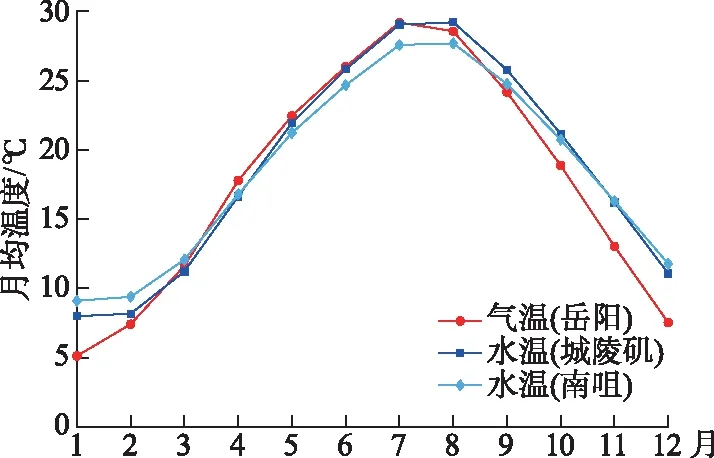
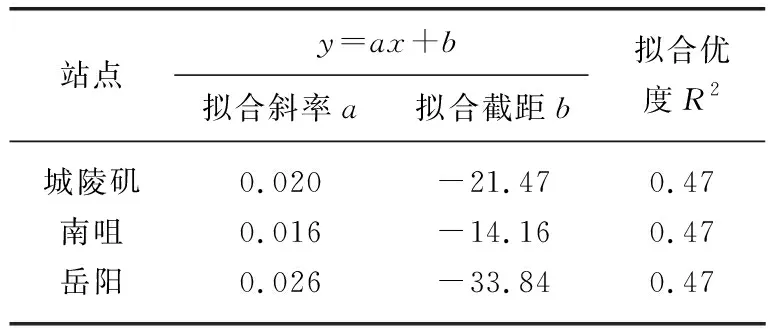
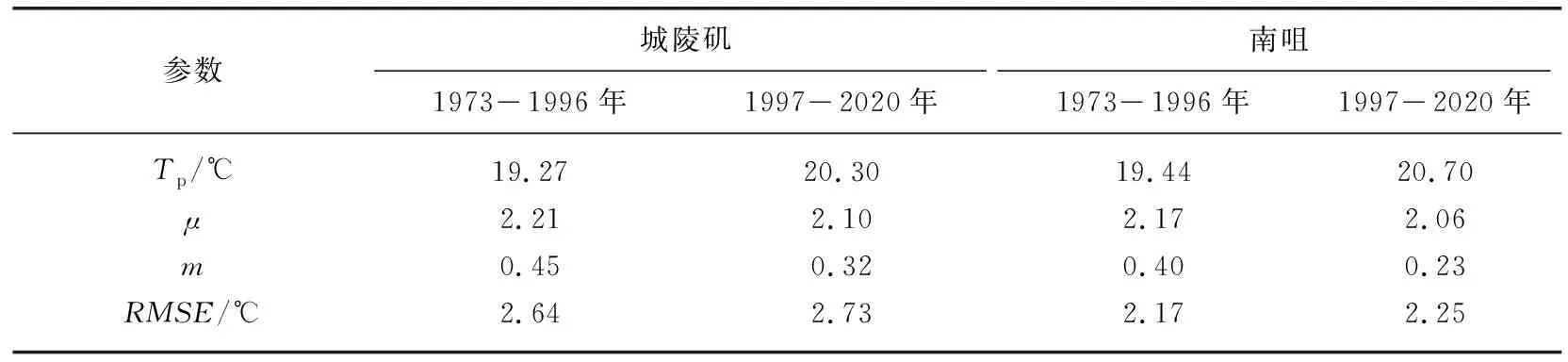
模型通过实测气温和水温数据对上述8个物理参数进行率定,并根据参数定义估计其合理变化范围,同时将时间步长设置为一日,采用四阶龙格-库塔格式求解常微分方程(2)[10]。Piccolroaz等对8个参数进行敏感性分析,证实p7、p8不具有良好的可识别性,并对模型进行简化。假设当Tw 本文选取常用的评价指标,即均方根误差(RMSE)和纳什效率系数(NSE)来系统地评估模型的模拟效果。RMSE值越小,表明模型预测误差越小;NSE值越接近于1,表明模型可信度越高。评价指标的具体定义分别为: (4) (5) 1.3.2 广义单位线法 Guo提出的广义单位线理论建立了描述S形增长曲线的一般函数表达式[20]。针对湖泊水温-气温的耦合关系及其演变问题,本文采用广义单位线法揭示水温随气温的演变特征,包括快速上升期、临界点和缓慢上升期的变化特征。建立水温-气温变化过程线的表达式为: (6) 其中, x(Ta)=exp[μ(Ta/Tp-1)] (7) 由式(6)和(7)进一步推导得到水温随气温变化的瞬时变化率u的表达式为: (8) 为了率定和验证Air2water模型,以2007-2018年岳阳站的日均尺度气温序列为模型驱动数据,将城陵矶站、南咀站的实测日均尺度水温序列分为两部分,其中2007-2014年的数据用于模型参数率定,2015-2018年的数据用于模型验证。图2为6参数模型率定和验证阶段实测水温与模拟水温的对比结果。模型的率定参数及评价结果如表1所示,其中率定期的RMSE对应最优参数集。由图2可知,率定期和验证期的散点基本紧密分布在y=x附近,表明模拟水温与实测值吻合较好。由表1可知,相比于率定期,验证期RSME较小,NSE较大。相比于南咀站,城陵矶站的散点更为集中,RSME较小,NSE较大。城陵矶站实测水温和模拟水温的绝对误差最大为4.45℃,出现在率定期;而南咀站为7.87℃,出现在验证期。可见城陵矶站的模拟结果优于南咀站。这是由于南咀站和岳阳站(气象站)之间的距离较远,应用条件存在差异,一定程度上影响模型的预测精度。此外,相比于率定期,模型不能直接捕捉到验证期间湖泊表层水体的太阳辐射、风扰动等影响因素的变化。因此,采用邻近气象站实测数据作为模型输入条件更为合理,结果的准确性、可靠性更高。同时在率定期间采用8参数模型进行参数敏感性分析,结果表明p7、p8的取值对模型效果无显著影响。 表1 Air2water模型的参数及评价结果Tab.1 The calibrated parameters and performance of Air2water model 图2 2007-2018年洞庭湖实测水温与模拟水温的对比:(a)城陵矶2007-2014年;(b)城陵矶2015-2018年;(c)南咀2007-2014年;(d)南咀2015-2018年Fig.2 Comparison between observed and simulated water temperature in Lake Dongting from 2007 to 2018:(a) Chenglingji during the calibration period; (b) Chenglingji during the validation period; (c) Nanju during the calibration period; (d) Nanju during the validation period 值得注意的是,Air2water模型存在一定的局限性,主要体现在其简单结构上,没有明确解释除气温以外的外部强迫因子(如太阳辐射、风速、相对湿度、湖泊形态等)对湖泊表层水温的影响。模型亦没有考虑水体透明度的变化及其可能对表层水体混合层深度产生的影响。事实上,湖泊表层水温是多个因子综合作用的结果,其变化特征不仅是对气象强迫的响应,也可能是对随机过程和不确定性因素的反馈,但模型无法模拟其具体作用。可见,模型率定参数的具体数值与率定期的湖泊属性和气候条件密切相关。如果考虑采用不同的率定期,最终模拟结果可能略有变化。总体而言,尽管Air2water模型是以简化的形式描述湖泊表层水温变化的主要物理过程(热分层现象),但仍能有效地重现水温的长期演变趋势,较好地反演水温-气温的耦合关系,在洞庭湖流域具有较好的适用性。 以1973-2020年岳阳站的日均尺度气温序列为Air2water模型驱动数据,2007-2014年城陵矶站、南咀站的实测日均尺度水温和气温序列为模型率定和验证数据得到的参数,采用Air2water模型重构1973-2020年洞庭湖的日均尺度水温序列,结果如图3所示,统计特征值如表2所示。由图3可知,日均水温、气温呈现以一年为周期的规律变化。岳阳站气温、城陵矶站水温、南咀站水温的多年平均值分别为17.70、18.74、18.55℃;多年平均极差分别为34.28、25.15、22.41℃。相对于气温,水温的多年平均值较大且变化幅度较小。由表2可知,城陵矶日均水温最高值为2013年8月11日的32.94℃;最低值为2008年2月3日的3.73℃。南咀日均水温最高值为2003年8月2日的31.04℃;最低值为2008年2月2日的5.19℃。城陵矶日均水温序列的方差为60.28(℃)2,南咀的为46.28(℃)2。相比于南咀,城陵矶的水温方差较大,历年最高温度较高,历年最低温度较低,波动比较剧烈,温度值离散程度较大。 图3 1973-2020年洞庭湖日均水温与日均气温的变化:(a)岳阳站气温;(b)城陵矶站水温;(c)南咀站水温Fig.3 Variation of daily averaged temperature in Lake Dongting from 1973 to 2020: (a)air temperature at the Yueyang Station; (b) water temperature at the Chenglingji Station; (c)water temperature at the Nanju Station 表2 1973-2020年洞庭湖日均水温与日均气温统计特征值Tab.2 Statistical characteristics of daily averaged temperature in Lake Dongting from 1973 to 2020 2.2.1 趋势性分析 洞庭湖逐月水温和逐月气温的多年平均值变化如图4所示。结果表明,48 a间两者的变化趋势基本一致,但水温变幅小于气温变幅。水温、气温的年内变化曲线较为规则,呈单峰变化且波动明显,在7、8月形成波峰,在12月、翌年1月形成波谷,即“夏季高、冬季低”,与太湖水温的年内变化规律相似[21]。水温极大值出现在8月,分别达到29.21℃(城陵矶)和27.68℃(南咀);极小值出现在1月,分别为7.99℃(城陵矶)和9.10℃(南咀)。以8月为分界点,2-7月作为升温期,气温以4.36℃/月的速率显著上升,水温分别以4.18℃/月(城陵矶)、3.64℃/月(南咀)的速率上升,水温较气温的升温速率慢;8月至翌年1月作为降温期,气温以4.69℃/月的速率显著下降,水温分别以4.24℃/月(城陵矶)、4.18℃/月(南咀)的速率下降,水温较气温的降温速率慢。水温变化的下降期比上升期短,湖水冷却比升温快,表明湖泊水温在不同季节的变化机理存在差异性。相对于气温而言,水温月际间变化较为平缓,变化幅度较小。月均水温开始下降的时间(8月)比月均气温(7月)延迟约1个月,与云南抚仙湖表层水温的研究报道吻合[22]。这主要归因于水体的比热容比空气的大,水温对热量变化的响应具有滞后性。 图4 1973-2020年洞庭湖月均水温与月均气温的变化Fig.4 Variation of monthly averaged water temperature and air temperature in Lake Dongting from 1973 to 2020 不同站点水温变化特征表现出空间差异性。由图4可知,在5-10月,城陵矶月均水温高于南咀,表明该时期洞庭湖月均水温空间分布呈现东高西低的态势;11月至翌年4月,城陵矶月均水温低于南咀,表明该时期洞庭湖月均水温空间分布呈现东低西高的态势。产生上述结果的原因可能是东洞庭湖位置靠北,水体面积较西洞庭湖大许多,湖盆形态、区域水文条件等因素导致水温的空间分布上存在差异。此外,城陵矶作为洞庭湖的唯一出湖口,其水温受长江干流的影响更大。 以时间为自变量,洞庭湖的年平水温、年平气温为因变量,采用一元线性回归拟合的方法分析其变化趋势,拟合结果如图5所示,拟合参数如所表3所示。其中拟合优度R2的值越接近1,表明回归直线对温度的拟合效果越好;反之,R2的值越小,表明回归直线对温度的拟合效果越差。R2定义为: (9) 从拟合结果(图5)可知,1973-2020年间,年均气温和年均水温的变化具有较高的一致性,均表现出冷暖交替、波动性变化的特点,总体呈上升趋势。2007年的年均气温最高,达到18.66℃;1984年的年均气温最低,为16.70℃。2018年的年均水温最高,达到19.55℃(城陵矶)和19.20℃(南咀);1984年的年均水温最低,分别为18.04℃(城陵矶)和17.96℃(南咀)。由表3可知,R2均较小(为0.47),这是由于洞庭湖流域内水温、气温波动频繁,线性拟合效果较差。各回归方程均通过α=0.05的显著性检验,表明水温、气温的上升趋势显著。城陵矶站、南咀站、岳阳站年均温度的上升速率分别为0.20、0.16、0.26℃/10 a,温度年极大值的上升速率分别为0.08、0.06、0.12℃/10 a,温度年极小值的上升速率分别为0.13、0.09、0.42℃/10 a。其中气温的上升趋势最为显著,在气温驱动下水温呈上升趋势,水温变化较气温更为平缓。上述结果指出的城陵矶站年均水温上升速率(0.20℃/10 a)略高于刘鹏翼等研究报道的1960-2010年城陵矶站年均水温上升速率(0.18℃/10 a)[23]。值得注意的是,2012年水温、气温偏低,可能受2011/2012年我国冬季气温异常偏低的影响[24]。相对于南咀站,城陵矶站的上升趋势更为明显,且年均水温偏高。在气候变暖的背景下,洞庭湖流域气温、水温有明显的上升趋势,但水温的上升速率低于全球湖泊表层水温的平均上升速率(即0.3℃/10 a[6-7])。 图5 1973-2020年洞庭湖年均水温与年均气温的逐年变化及变化趋势:(a)城陵矶站年均水温与岳阳站年均气温;(b)南咀站年均水温与岳阳站年均气温Fig.5 Interannual variation and trend of annual mean temperature in Lake Dongting from 1973 to 2020:(a)annual mean water temperature at the Chenglingji Station and annual mean air temperature at the Yueyang Station; (b) annual mean water temperature at the Nanju Station and annual mean air temperature at the Yueyang Station 表3 1973-2020年洞庭湖年均水温与气温的一元线性回归拟合参数Tab.3 Linear regression model parameters of annual mean water and air temperature in Lake Dongting from 1973 to 2020 2.2.2 突变性分析 从1973-2020年洞庭湖年均水温、年均气温距平及累积距平的逐年变化趋势(图6)可以看出,年均气温距平绝对值最大,表明气温较水温不稳定性更大。在1973-1996年年均水温距平主要是负值,为相对冷期;而在1997-2020年水温距平主要是正值,且近8年的水温距平均为正值,为相对暖期。年均水温、年均气温的累积距平曲线出现拐点的时间一致,均在1996年附近,且拐点前后累积距平曲线均呈现先下降后上升的趋势。结合运用累积距平法、滑动t检验方法和M-K检验方法,判定洞庭湖的年均气温和水温存在一个显著变暖的突变点,为1996年。气温突变结果与彭嘉栋等的研究结果(1997年)较为接近[25]。可见在1973-2020年间,洞庭湖先是经历一个缓慢的增温过程,但1996年气温、水温发生由低到高的跃变,此后湖区进入一个快速的增温时期。 图6 1973-2020年洞庭湖年均水温与年均气温距平及累积距平的逐年变化Fig.6 Interannual variation of annual mean temperature anomaly and accumulated anomaly in Lake Dongting from 1973 to 2020 以突变年份1996年为界,将研究时段划分为突变前(1973-1996年)和突变后(1997-2020年)两个阶段。岳阳站、城陵矶站、南咀站的多年平均温度从1973-1996年的17.32、18.45、18.31℃升高至1997-2020年的18.07、19.04、18.79℃,较之前24年分别增加0.75、0.59、0.48℃,增幅分别为4.3%、3.2%、2.6%。将夏、秋季(6-11月)定义为暖季,冬、春季(12月至翌年5月)定义为冷季,暖、冷季平均温度的变化趋势如图7所示。结果表明,城陵矶的暖季平均水温变化速率从0.02℃/10 a升高至0.12℃/10 a,冷季从0.004℃/10 a升高至0.10℃/10 a;南咀的暖季平均水温变化速率从0.02℃/10 a升高至0.10℃/10 a,冷季从-0.004℃/10 a变为0.08℃/10 a。1973-1996年,暖季平均温度呈微弱的上升趋势;冷季平均温度以波动为主,无明显变化趋势。1997-2020年,水温、气温的年际间波动起伏加剧,暖季、冷季内的冷暖交替更为频繁,暖季持续变暖且速率增大,冷季转变为升温趋势。突变前后暖季、冷季水温的变化机制不同,但均是变暖的积极作用占主导。此外,1996-1997年冷季平均温度存在明显的由冷至暖的状态跃迁。可见1996年洞庭湖流域的突变式增温主要是由冷季的显著增暖过程驱动的,即冬季、春季增温效应对变暖的贡献较大。 图7 1973-2020年洞庭湖暖季(a)与冷季(b)平均水温和气温的逐年变化(阴影分别表示1973-1996年和1997-2020年两个阶段)Fig.7 Interannual variation of annual mean temperature during warm season (a) and cold season (b) in Lake Dongting from 1973 to 2020 由结果分析部分可知,从日、月、年的尺度来看,水温整体随气温变化,水温对气温的响应程度较强,水温变化幅度较气温小,且水温变化趋势较气温更为平缓。但在不同时间尺度上,水温与气温的相关性具有一定差异。月均水温变化比月均气温延迟约1个月(图4),水温具有滞后性;而年均气温和年均水温的变化趋势具有明显的一致性(图5),水温的滞后性并不明显。由此可见,随着时间尺度的增大,滞后效应减弱,使得水温、气温趋向于同步变化。值得注意的是,气温通常是影响水温演变的主要因子。由于大气与表层水体相接触,并且以长波辐射和感热交换的方式直接作用于水体,水体内储存热量变化,水面温度随之改变。因此,湖泊表层水温是湖泊热量平衡状态的直接反映,其长期变化趋势是揭示气候变化驱动水温变化的有效手段和途径。由于气候变化具有不确定性,加上湖泊自身的物理特性,湖泊对气候变暖的响应亦具有复杂性和多变性。随着气候变暖,气温上升通过影响长波辐射、水气界面热交换、湖面蒸发等调节湖泊表面热收支,从而驱动湖泊表层水温变化[26]。 通过对实测水温及气温资料分析可知,水温-气温变化过程线分布与广义单位线相似。因此,为了深入探究水温-气温之间的耦合关系及其演变,以日均气温为自变量,日均水温为因变量,采用广义单位线法建立两者之间的耦合关系模型,结果如图8所示,参数如表4所示,其中模型计算得到的均方根误差RMSE介于2.17~2.73℃,表明拟合效果良好。结果表明,水温对气温变化的响应程度强,两者之间呈现显著的正相关关系。水温随气温的变化速率呈负偏分布,当气温Ta较低时,水温随气温升高而缓慢上升;随着Ta持续上升,水温随气温的瞬时变化率u(Ta)先增大,增到最大值后减缓,u(Ta)最大值相对应的气温即为临界气温值Tp。当大气与水体的热量交换至一定程度时,有限的热量所引起水温的变化量减小,但水温仍随气温上升而上升。当气温低于0℃或高于35℃时,u(Ta)小于0.01℃-1,表明水温-气温的耦合关系相对较弱。可见气温在驱动水温变化的同时,制约着水温变化。洞庭湖流域于1996年发生突变式增温后,城陵矶的Tp从19.27℃增大至20.30℃,μ从2.21减小至2.10,m从0.45减小至0.32;南咀的Tp从19.44℃增大至20.70℃,μ从2.17减小至2.06,m从0.40减小至0.23(表4)。水温随气温变化的临界气温值上升1℃左右。无论是快速上升期还是缓慢上升期,水温随气温的变化速率均略有减小,表明水温对气温响应的敏感性降低,水温-气温的耦合关系有所削弱。这可能与黎鹏等研究指出的2003-2017年洞庭湖流域水位总体呈上升趋势有关[14]。由于小而浅的湖泊往往比大而深的湖泊更易增暖[27],因此随着湖泊水深的增大,水体的透光层上升,光的衰减程度减弱,水温对气温的响应速率有所减小,水温-气温耦合关系有所削弱[28]。针对洞庭湖水位变化对水温长期演变趋势的影响有待进一步深入研究。此外,岳阳的最低气温从突变前的-6.00℃升高至突变后的-3.04℃,最高气温从突变前的34.02℃升高至突变后的34.72℃。当气温持续升高,大气持水能力的增加促进湖面的蒸发冷却,且水温升高使得湖面的逆辐射相应加强,阻止水温进一步升高[29-30]。由此可知,水温-气温的耦合关系削弱可能与水温、气温的持续上升趋势存在一定的关联性。 图8 1973-2020年洞庭湖水温-气温变化过程线及水温随气温变化的瞬时变化率:(a)城陵矶1973-1996年;(b)城陵矶1997-2020年;(c)南咀1973-1996年;(d)南咀1997-2020年Fig.8 S-hydrograph and instantaneous unit hydrograph applied to water temperature and air temperature in Lake Dongting from 1973 to 2020: (a) Chenglingji before mutation; (b) Chenglingji after mutation; (c) Nanju before mutation; (d) Nanju after mutation 表4 1973-2020年洞庭湖水温-气温的广义单位线模型参数Tab.4 Model parameters of the general unit hydrograph applied to water temperature and air temperature in Lake Dongting from 1973 to 2020 本文针对水温的长期演变趋势问题,基于长序列的实测气温资料,采用Air2water数据驱动模型重构出洞庭湖1973-2020年的水温序列,结合数理统计方法研究湖泊表层水温在气象条件驱动下的演变特征,得出以下主要结论: 1)尽管Air2water模型以常微分方程的简化形式概化湖泊的热力学过程,存在一定的局限性,但采用模型重构1973-2020年洞庭湖日均尺度水温序列具有较高的可信度。通过验证Air2water模型的准确性可知,RMSE均在合理范围内,且NSE均接近于1,实测水温与模拟水温吻合良好,表明该模型可较准确地反演水温的长期演变趋势,在洞庭湖流域有较好的适用性,是一种预测湖泊表层水温的有效方法。 2)在时间尺度和空间尺度上水温的变化特征呈现出差异性。1973-2020年,从年内变化来看,洞庭湖水温波动明显,呈现夏高冬低的季节变化特征。水温有明显的上升期和下降期,且降温过程较升温快。从年际变化来看,在气候变暖驱动下年平均水温呈现持续的波动性上升趋势,且1996年发生突变之后上升趋势更为显著,其中城陵矶和南咀年均水温的上升率分别达到0.20和0.16℃/10 a。1996年洞庭湖流域的突变式增温主要是由冷季的显著增暖过程驱动。相对于南咀站,城陵矶站水温的升温趋势更为显著。整体而言,水温随气温变化而变化,水温变化幅度较小且变化趋势较为平缓,具有滞后性。 3)采用广义单位线法建立水温-气温之间的耦合关系,水温随气温上升的速率先增长至极大值后逐渐减缓。洞庭湖于1996年发生突变式增温后,城陵矶的Tp从19.27℃增大至20.30℃,μ从2.21减小至2.10,m从0.45减小至0.32;南咀的Tp从19.44℃增大至20.70℃,μ从2.17减小至2.06,m从0.40减小至0.23。水温随气温的变化速率略有减小,表明水温对气温响应的敏感性降低,水温-气温的耦合关系有所削弱。

2 结果分析
2.1 Air2water模型的率定与验证


2.2 水温演变特征分析
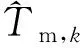



3 讨论

4 结论

