基于FFT算法的低频信号失真度测量装置优化设计
俞达,陈冬英,安南,谢孔亮
基于FFT算法的低频信号失真度测量装置优化设计
俞达1,陈冬英1,2,安南1,谢孔亮1
(福建江夏学院 1. 电子信息科学学院,2. 数字福建智能家居信息采集及处理物联网实验室,福建 福州 350108)
总谐波失真(THD)是运算放大器、功率放大器等器件的主要衡量参数之一.设计以TMDSSK3358开发板为硬件基础,以FFT算法为核心的高精度快速信号失真度测量装置.传统的模拟测量法不仅硬件设计复杂,且性能受限于滤波器.该设计利用AD转换实现模拟信号与单片机可接收的数字信号转换,采用FFT(快速傅里叶变换)实现信号的时频转换,通过获得幅频信息进而得到各个谐波的功率,最后所测的THD值通过TMDSSK3358开发板上的液晶屏模块显示.测量结果表明,该设计在频率为1 kHz时测量精度误差小于0.05%,失真度测量与显示用时不超过 10 s.与传统的信号失真度测量装置对比,在简化硬件复杂度时,速度更快、精度更高,为FFT算法应用于失真度测量提高新的研究思路.
信号失真度测量;FFT算法;AD转换:总谐波失真
总谐波失真(Total Harmonic Distotion,THD)是信号的主要参数之一,表征信号偏离正弦波的程度[1].对于波形测量,优先关注的性能指标是实际所得信号和原始输入信号是否存在失真.一般情况而言,相对于“简单”波形,如常规方波、正弦波,实际信号和原始信号是否一致性,利用该波形的典型参数即可实现判断,如信号的幅值、频率、周期或者相位偏移、频率偏移等.更进一步,也可以采用信噪比等复杂参数作为重要衡量标准.但是判断复杂的波形,参数法可能不再有“典型”意义(如幅度或者频率),或者不能正确实现定义(如信号的信噪比).同时,若通过是否具有相同有效值法,也不能唯一校准波形的失真情况.因这些方法受人们的主观判断影响比较大,所以采用波形定量值“失真度”恰好能够很好地衡量两个波形一致的程度[2-3].
失真度测量广泛涉及各类仪器精确度问题,传统失真度测量仪器,主要是模拟法,核心通过设计滤波器,以此滤除输入信号中基频分量,从而获得各个谐波值.该设计法所获得的测量精度由滤波器性能决定,且硬件相对较为复杂[4],而本文采用数字式失真测量方法,在保证提高精度与速度基础上,大幅度降低外界噪声干扰.
1 总体的设计方案
本设计以TMDSSK3358开发板为硬件基础,采用FFT算法(Fast Fourier Transform 快速傅立叶变换)为核心,实现对不同频率和幅度的信号失真度的测量.首先,采用模数转换(analogue-to-digital conversion,ADC)将模拟信号放大并转化为数字信号;其次,利用欧拉公式实现实部虚部的分离,并通过基-2蝶形的FFT算法,实现信号的时频转换,获得幅度谱,进而获得各个谐波的各类功率;第三,利用THD,即总谐波失真的定义式进行计算得到最后的失真度;最后,将测量THD与理论THD进行对比分析,并进行输出.本文采用FFT算法将信号失真度的计算参数进行优化,将电压幅值关系转为功率值关系运算,大大提高计算精度与速度.
总体设计框图见图1.通过AD进行输入信号放大采用,并进行数字化处理,然后利用FFT算法进行时频转化,以单片机实现系统的控制,完成信号幅度谱的获取,并获得双边频带的功率谱,计算基本功率、总功率、各次谐波功率和,最后完成失真度的计算.该设计不仅降低模拟测量中设备繁杂度,同时有效提高了整个系统的精确度和运行速度.

图1 模块设计流程
2 基于FFT算法的改进失真度测量装置设计
2.1 AD模块
该装置的输入信号为模拟信号,为适应嵌入式处理器可处理的,采用ADC模块将其转为数字量.本文选用TMDSSK3358开发板内置的SAR ADC(逐次逼近寄存器型模数转换器),SAR ADC基本架构见图2.
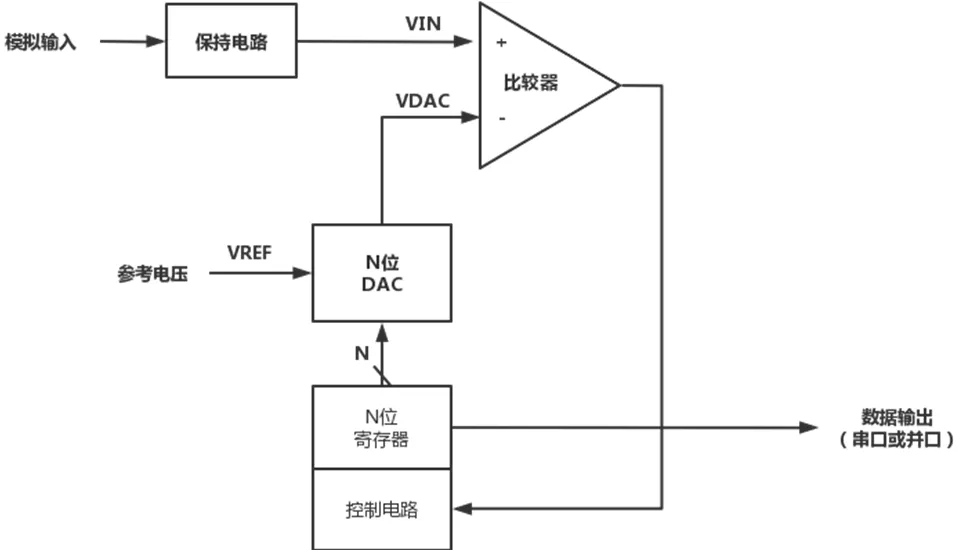
图2 SAR ADC基本架构
模拟输入的电压(VIN)进行数字化需通过采样——保持——量化——编码,经过采样后的数据,进一步量化处理,主要采用二进制搜索算法实现.具体步骤为:(1)N位寄存器所设置值为中间刻度100….00,其中,MSB初始化为1.(2)再将DAC输出(VDAC),将其取值为VREF/2,VREF为ADC的基准电压.(3)比较判断VIN与VDAC的关系.若输入电压值比VDAC大,那么比较器输出结果为高电平(1),同时将N位寄存器中MSB置为1.若输入电压比VDAC小,那么比较器输出结果为低电平(0),同时将N位寄存器中MSB清零.(4)将SAR控制逻辑向下移动一位,同时设置其为高电平,并与下一次完成比较.此过程一直持续,直至LSB.完成上述操作,即实现了模拟信号与数字信号的转换,所得的N位转换结果储存在寄存器内,最后通过串口(或并口)进行输出[5-7].
2.2 FFT算法
对于测量信号参数的转化涉及整周期同步采样和 FFT 处理.
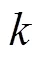
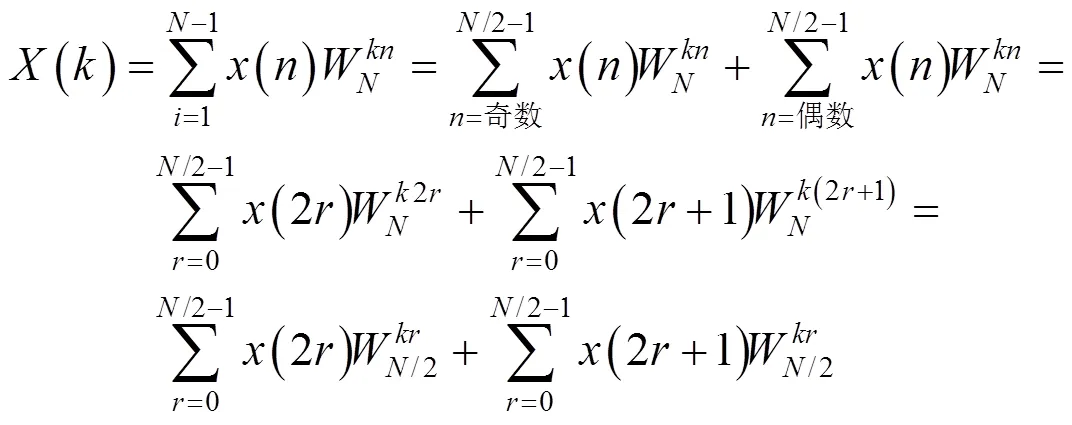
其中

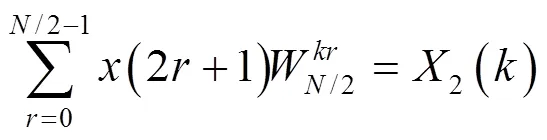
则式(1)可化成

蝶形运算单元见图3.

图3 基2 DIT-FFT
本设计的FFT设置点数为4 096(212,FFT点数只能为2的倍数),即对ADC读到的4 096个点进行FFT转换,得到频域数据[8-9].
2.3 失真度计算
通过FFT算法可获得信号对应的频域数据.因所得的第1个数据为常数,即为直流分类,因此,去掉第1个数据,由此获得信号的频谱[12].若一个周期正弦振荡信号出现失真,其具有基波分量(频率为基本频率)及多次谐波分量.将该失真的周期信号按傅里叶级数展开
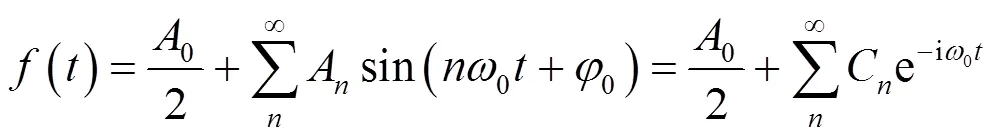
其中

常见方法中信号的失真采用失真度来衡量.失真度的测量方法即把各次谐波的电压有效值平方后,再累加,最后开根号的结果与基本波形电压有效值进行相除获得所需的失真度值[13-14].本文采用FFT算法获得各个信号的频谱,求得对应的平均功率,获得相应的失真度值

利用功率来计算谐波失真度,可以得到噪声信号总功率,即可以求出由噪声引起的误差.具体实现流程见图4.

图4 基于FFT的失真度测量方法流程
3 设计结果与分析
本设计采用Tektronix双踪示波器、普源DG4162信号发生器和TMDSSK3358开发板完成测试.该装置适用于各种常见波形测量,包括方波、正弦波、三角波等.因篇幅有限,该测试结果以最典型的正弦波为例进行说明.部分测量结果见图5a~f,具体结果分析见表1.

图5 部分正弦波信号失真度测量结果

表1 测试过程结果
由表1分析可知,该装置可以实现的功能:
(1)输入信号的峰值电压范围为30~ 600 mV;
(2)输入信号基频为1~100 kHz;
(3)输入信号失真度测量误差绝对值THD-THD ≤0.05%;
(4)失真度测量与显示用时不超过 10 s.
为进一步对比验证该设计功能,将传统滤波法实现结果与本文实现结果进行对比(见表2).因低频段信号失真度较难检测,因此主要以低频为参考数据.通过对比,本设计的误差比传统的滤波法小0.05%,同时与文献[4]进行对比,在相同频率、相同幅值,且均采用数字化基础上,本设计失真度误差比文献[4]降低了0.5%左右.因此,本文改进后的装置在简化硬件复杂度的基础上,精度更高,具有很好的应用前景.

表2 测试结果对比
4 结语
本文为了克服模拟失真度测量仪硬件上的复杂,且受限于滤波器的性能问题,设计了一个以TMDSSK3358开发板为硬件基础,以FFT算法为核心的信号失真度测量优化装置.该设计利用AD转换将模拟信号转换成单片机可以接收的数字信号,利用FFT实现信号的时频转换,获得幅频信息进而计算出各个谐波的功率,最后将得到的THD值通过TMDSSK3358开发板上的液晶屏模块显示.测量结果表明,本设计能够快速精确实现失真度测量并显示,与传统方法对比,该装置精度可以提高近0.05%,为FFT算法应用于失真度测量提高新的研究思路.
[1] 孙璟宇,王中宇,梁志国.任意波形失真度的一种评价方法[J].北京航空航天大学学报,2015,41(1):33-37.
[2] 李翔,陈实.时频结合的失真度测量方法研究[J].国外电子测量技术,2017,36(1):27-30.
[3] 赵二刚,王艳芳,张维.低频信号失真度测量系统设计[J].自动化与仪表,2019,34(12):53-56,60.
[4] 丁跃浇,陈松,荣军,等.数字正弦信号失真度测量仪的设计[J].微型机与应用,2015,34(12):64-66,69.
[5] 杜兆凯.基于FFT的便携式频谱仪的设计与实现[D].西安:西安建筑科技大学,2019.
[6] 张煜欣.14位SAR ADC的电路设计[D/OL].哈尔滨:哈尔滨工业大学(2021-02-16).DOI:10.27061/d.cnki.ghgdu.2021.003054.https://kns.cnki.net/.
[7] 孟昊.16位逐次逼近型ADC设计[D/OL].成都:电子科技大学(2021-02-16).DOI:10.27005/d.cnki.gdzku.2021.001535.https://kns.cnki.net/.
[8] 周俊,刘明,邱爱兵.基于FPGA的基2-FFT算法在谐波检测系统中的研究[J].电力电容器与无功补偿,2016,37(6):100-104.
[9] Przybyla P.A pattern recognition method for lattice distortion measurement from HRTEM images[J].Journal of Microscopy, 2012,245(2):200-208.
[10] 余晓明,吴捷,王世闻,等.基于DSP的通用FFT算法在电网谐波检测中的应用[J].北京联合大学学报(自然科学版),2007(3):28-32.
[11] Wilkerson J R,Gard K G,Steer M B.Automated Broadband High-Dynamic-Range Nonlinear Distortion Measurement System[J].IEEE Transactions on Microwave Theory and Techniques,2010,58(5):1273.
[12] Komuro T,Sobukawa S,Sakayori H,et al.Total Harmonic Distortion Measurement System of Electronic Devices up to 100 MHz with Remarkable Sensitivity[J].IEEE Transactions on Instrumentation and Measurement,2007,56(6):2360-2368.
[13] Won P K,Whan S D,Chul R Y.Implementation of MultiBand-Digital Passive InterModulation Distortion Measurement System[J].The Journal of the Korea Institute of Electronic Communication Sciences,2016,11(12):1193-1200.
[14] Zhang Jun,Chen Qian,Zhou Nanguang.Correlation analysis with additive distortion measurement errors[J].Journal of Statistical Computation and Simulation,2016,87(4):664-668.
Optimal design of low frequency signal distortion measuring device based on FFT algorithm
YU Da1,CHEN Dongying1,2,AN Nan1,XIE Kongliang1
(1. School of Electronic Information Science,2. Smart Home Information Collection and Processing on Internet of Things Laboratory of Digital Fujian,Fujian Jiangxia University,Fuzhou 350108,China)
Total Harmonic Distortion(THD)is one of the main measuring parameters of operational amplifiers, power amplifiers and other devices. This design is a high-precision signal distortion measuring device based on the TMDSSK3358 development board and FFT algorithm. The hardware design of traditional analog measurement method is complex, and its performance is limited by the filter. First of all, the design uses AD conversion to realize the conversion between analog signals and digital signals that can be received by the microcontroller.Secondly, FFT (Fast Fourier Transform)is used to realize the time-frequency conversion of the signal, and the power of each harmonic is obtained by obtaining the amplitude frequency information.Finally,the measured THD value is displayed by the LCD module on the TMDSSK3358 development board.The measurement results show that the measurement accuracy error of this design is less than 0.05% when the frequency is 1 kHz, and the measurement and display time of distortion is not more than 10 s.Compared with the traditional signal distortion measurement transpose, it is faster and more accurate when simplifying the hardware complexity,which improves a new research idea for FFT algorithm applied to distortion measurement.
signal distortion measurement;FFT algorithm;AD conversion;total harmonic distortion
1007-9831(2022)11-0047-06
TH77
A
10.3969/j.issn.1007-9831.2022.11.009
2022-05-27
福建江夏学院2022年大学生创新创业训练计划项目(202213763157);2022年大学生创新创业训练国家级计划项目(202213763023);福建省教育厅中青年教师教育科研项目(JAT210359);福建江夏学院校级科研人才培育项目(JXZ2021011)
俞达(2001-),男,福建泉州人,在读本科生.E-mail:1923087745@qq.com
陈冬英(1989-),女,福建三明人,讲师,硕士,从事电子信息类器件研究.E-mail:863848737@qq.com

