模糊区间点二列相关系数和多系列相关系数
王鑫蕊,窦鑫莹,杨志清,施建华,2,3,4
模糊区间点二列相关系数和多系列相关系数
王鑫蕊1,窦鑫莹1,杨志清1,施建华1,2,3,4
(1.闽南师范大学 数学与统计学院,福建 漳州 363000;2.福建省粒计算及其应用重点实验室,福建 漳州 363000;3.福建省数据科学与统计重点实验室,福建 漳州 363000;4.数字福建气象大数据研究所,福建 漳州 363000)
在探讨2个随机变量的相关性研究中,随机变量型态已由相同型态扩展至混合型态.然而,在混合随机变量组合的条件下,当数据呈现模糊区间型态时,传统相关系数演算法将不适合使用.借鉴传统点二列相关系数研究成果,基于二分类与连续型以及多类别与连续型等混合型随机变量组合,提出了模糊区间点二列相关系数和模糊区间多系列相关系数的改进算法,并通过蒙特卡洛模拟和实证分析,验证了该方法的有效性.
模糊区间;点二列相关系数;模糊区间点二列相关系数;模糊区间多系列相关系数
自19世纪80年代皮尔逊(Pearson)首次提出了皮尔逊积差相关系数的演算方法之后,研究2个随机变量间相关性的风潮随之开启.与相关图和相关表2种传统的方法不同,相关系数可以将相关性进行量化说明,更直观地反映出变量间相关关系的强弱.皮尔逊积差相关系数是用线性关系的方式来衡量连续型随机变量的相关性,取值介于区间,当相关系数为正数时表示2个变量呈现正向相关,当相关系数为负数时表示2个变量呈现负向相关,系数值越接近于0,则相对表示2个随机变量的相关程度越弱.然而,对于离散型随机变量或定序型随机变量,将无法通过皮尔逊积差相关系数来衡量随机变量间的相关性,学者们为了探讨离散型随机变量或定序型随机变量的相关性,提出了等级相关系数方法,如Spearman等级相关系数和Kendall等级相关系数,它们都是利用排序秩差的方式来衡量分级定序变量之间的相关性.
此外,当2个变量是离散变量中的类别变量或连续变量中的定距变量时,往往需要根据变量的特性导入不同的相关系数演算方法,从而更准确地计算变量间的实质相关程度[1].在类别变量的部分,一般采用Harald Cramer于1946年提出的Cramer′s V系数进行变量的相关性探讨,当2个变量完全相关时取值为1,完全独立时取值为0.然而,对于类别变量与定距变量混合型态的数据集,变量之间的相关性无法根据之前所提及的方法进行衡量.1960年,Gupta[2]讨论了类别变量与定距变量间相关性的问题,推导了一般情况下点二列相关系数的大样本标准差公式,同时引入了多序列相关系数,并进一步研究了它的一些性质.
近年来,在类别变量与定距变量混合的环境条件下,相关混合数据开始逐渐涌现,如医疗领域中对于疾病治愈和用药量的关系,教育领域中学生高考录取和会考成绩间的关系等,反映了混合型态的数据已成为各领域所亟需重视的方向.在投资学中,点二列相关系数可以被用来研究投资者人格与投资行为的关系,有利于据此提出有针对性的投资建议[3].在教育领域中,文献[4]利用点二列相关系数研究语言偏误与学生性别、年龄和社会环境间的相关性,研究结果说明了学生书面表达中存在的偏误与语文学业成绩呈现负相关,同时与性别、年龄和社会环境之间也存着在不同程度的相互影响;Vincent[5]等在考试环境下,通过点二列相关系数对实际数据进行了相关性分析,并对如何利用点二列相关系数解决实际问题进行了介绍.在医学领域中,曹盼盼[6]等利用点二列相关系数公式分析了年龄、平均收缩压、空腹血糖、血清白蛋白等与蒙特利尔认知评估量表(MoCA-B量表)评分的相关性,研究结果对老年慢性肾脏病的预防与治疗起到了积极作用.
随着现代数据收集的更新演化,现实所观测到的数据发生了量与型态上的改变,数据采集的过程中变量的生成方式也由传统的单变量转变为区间型态变量,这也促进了区间数据统计分析方法的演进[7-8].从相关系数的研究进程来看,模糊区间相关系数已经被提出[9-11].但模糊区间相关系数大部分被用于衡量具有同一变量型态的模糊区间变量间的相关性[12],对于混合型态的模糊区间变量具有一定的局限性.本文将传统的点二列相关系数方法进行创新,针对单一类别变量与模糊区间定距变量混合型态的数据集,提出模糊区间点二列相关系数这一新方法,并将其推广到多类别变量与模糊区间定距变量的相关系数研究,进一步扩展了混合型态数据的应用层面,丰富和发展了多元化数据型态的相关性理论研究.
1 模糊区间点二列相关系数及多系列相关系数设计
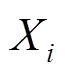
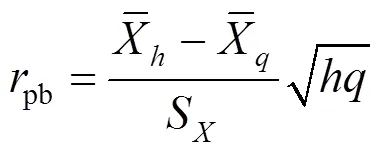
1.1 模糊区间点二列相关系数
由于传统的点二列相关系数在多元化数据型态下具有局限性,它对于区间型数据不再适用.因此,本文基于传统的点二列相关系数方法提出模糊区间点二列相关系数的新定义,用以探讨一组区间随机变量和一组分类变量间的相互影响关系.具体地,模糊区间点二列相关系数(Point Biserial Correlation Coefficient of Fuzzy Interval,PBCCFI)的定义为:



1.2 模糊区间多系列相关系数


由于传统的多系列相关系数公式比较复杂,人们往往需要借助类别变量上下限的正态曲线高度和正态分布表来计算.为了方便计算,本文提出了先将多类别变量转化为二分类变量,再由模糊区间点二列相关系数公式来估计模糊区间连续变量与名义变量间相关性的方法,由此得到模糊区间多系列相关系数(Multiserial Correlation Coefficient of Fuzzy Interval,MSCCFI).
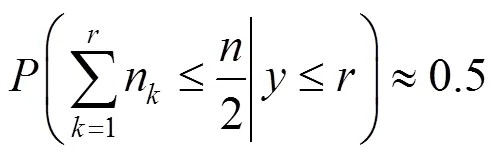
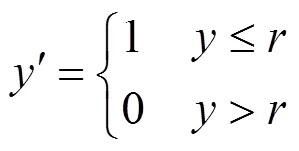
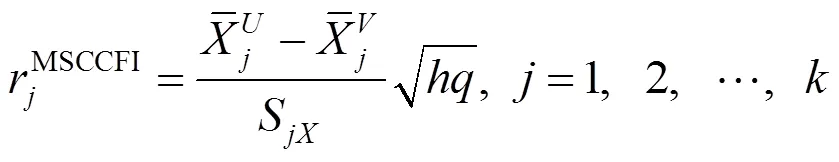


2 蒙特卡洛模拟
采用蒙特卡洛(Monte Carlo)方法对模糊区间点二列相关系数及模糊区间多系列相关系数进行模拟分析,通过模拟结果对该方法的效果进行评估.
2.1 模糊区间点二列相关系数
在模糊区间点二列相关系数的演算过程中,可以通过蒙特卡洛模拟方法对所提出的相关系数方法进行验证,其模拟步骤为:



表1 模糊区间点二列相关系数
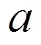
王某表现得一点儿也不跋扈,但有犀利的网友读出了“威胁”:虽说这张关系谱里没啥级别了不得的官员,但不乏“关键岗位”的人物。譬如表姐夫、姥爷的同事,和教育系统关系密切,说不准还会影响到老师的前途。所以即便关系不算近,也要“强蹭”一把。这就有点绵里藏针的味道了。
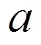
2.2 模糊区间多系列相关系数
在模糊区间多系列相关系数的演算过程中,应用蒙特卡洛模拟方法对模糊区间多系列相关系数的效果进行验证,其模拟步骤为:


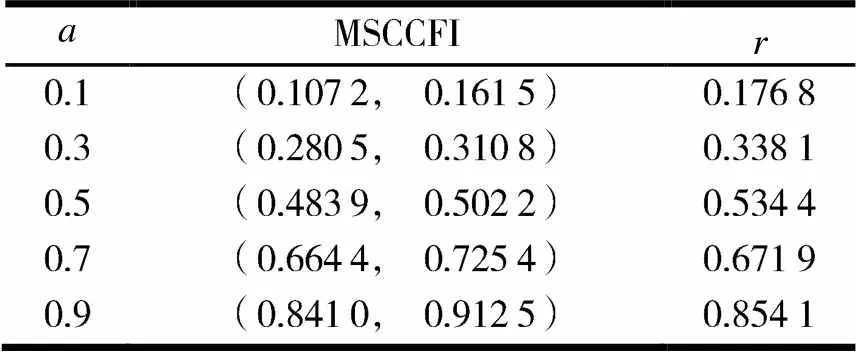
表2 模糊区间多系列相关系数


3 应用研究
从金融机构的信用贷款角度来看,金融机构在提供信贷专案时,也希望能在风险最小的情况下进行,也就是说个人或企业在申请信用贷款时,金融机构将对个人或企业的信用进行评估,并作为核发贷款的依据.因此,在金融产业领域中,对申请信用贷款的客户进行信用评等审核,已成为金融机构核拨贷款的常规做法,同时也反映出信用评等与贷款审核结果之间存在着相互影响的程度[16].鉴于此,为了研究信用贷款审核结果和信用评等之间的关系,本文引用2019-01—2019-12某银行的2个地区分行(分别记为A分行,B分行)的微小企业信贷计分卡总分及贷款审核结果等数据,进行模糊区间点二列相关系数的实证分析.
根据地区各采集了50位贷款申请用户的数据,分别采取其信用评等计分的最低分和最高分组成区间数值,使其信用评等以区间型态呈现,同时记录用户的信用贷款审核结果.具体数据见表3.
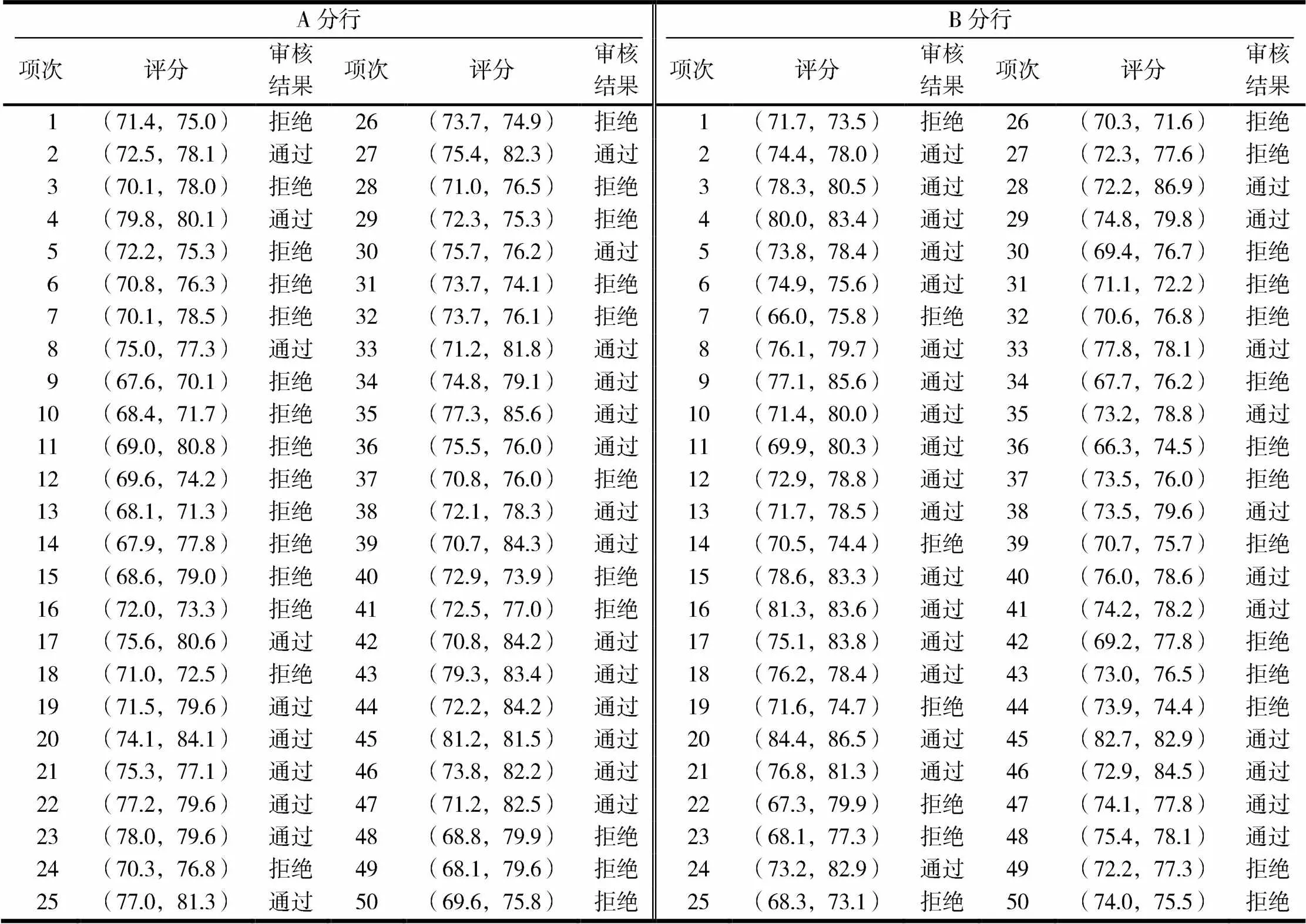
表3 微小企业信贷的信用评等与贷款审核结果数据统计
该银行在A,B分行中,一般以信用评等总分作为衡量贷款申请客户信用状况的依据.然而为了避免单一信用评等总分易造成信用误评的现象及更好地维护客户权益,部分银行采用了双重信用评等方式对贷款申请人进行信用评等.
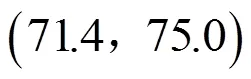
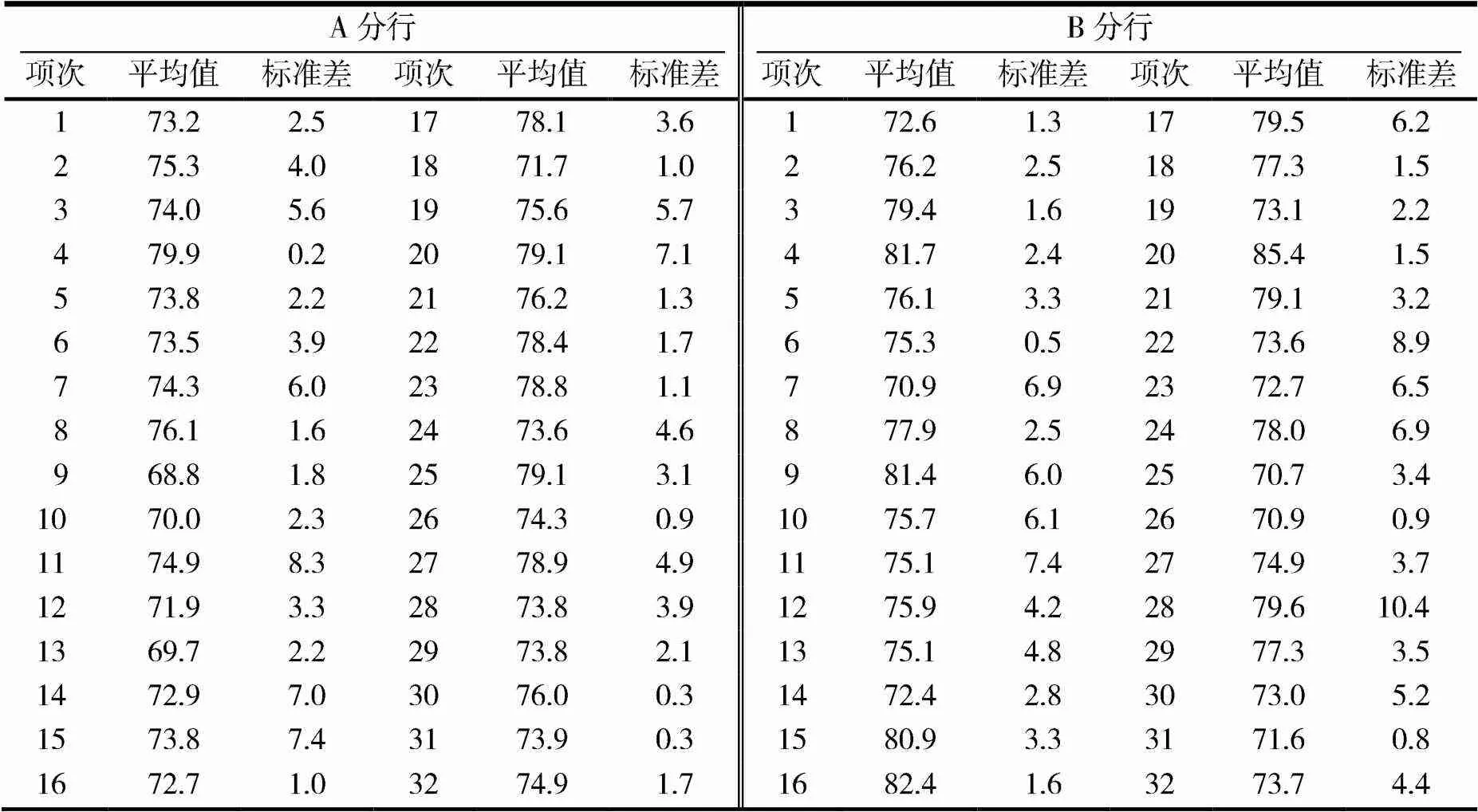
表4 微小企业信贷的信用评等的描述性统计

续表4
平均值可以反映信用评等总分的集中趋势,但单从平均值来看,无法判断样本观测点的大致分布情况,因此必须结合标准差统计量的数值进一步对数据进行分析,最后通过均值和标准差2个统计量刻画出数据的集中和离散程度.如在A分行的部分,以第4项数据为例,其平均值为79.9,数值较大,而其标准差为0.2,数值较小,此时可以认为该项数据的2种信用评分均较高且差异很小,说明该用户有很大可能通过审核,这一结果与实际审核结果相一致,说明了描述性统计分析在数据分析中有至关重要的作用.在B分行的部分,以第26项数据为例,其平均值为70.9,标准差为0.9,说明该用户的2种信用评分均较低且较为接近,可以猜测该用户的审核结果应为拒绝,这也与实际审核结果相符.另外,当数据的平均值和标准差值均处于居中水平时,则无法通过描述性统计分析对审核结果进行判断.
利用模糊区间点二列相关系数对信用评等总分与审核结果之间的相关性进行量化分析,结果见表5.

表5 信用评等总分与贷款审核结果的点二列相关系数


相关,而最低总分与该分行的信用贷款核拨不相关.表明该分行进行信用贷款核拨时更关注客户信用评等的最高分,即客户信用评等总分的最低分较低时,若最高分足够高,该客户有很大可能通过贷款审核.
4 结语
本文提出的模糊区间点二列相关系数和模糊区间多系列相关系数方法,适用于模糊区间类别变量相关性分析的一类问题,能有效地度量混合型模糊区间随机变量的相关性.其中,模糊区间点二列相关系数方法与传统点二列相关系数相比最大的优势是可以保持数据的维度不被改变,将搜集到的区间观测信息充分利用起来,得到的结果不仅可以体现2个变量间的相关性,还可以呈现变量改变时相关性变化的程度.而模糊区间多系列相关系数的优点在于其不仅简化了多系列相关系数的演算过程,而且使多维数据在分析过程中保持维度不变,保证了数据信息的完整性,从而使分析结果更具有说服力,为决策者提供更合理的参考依据.
[1] 金林,李研.几种相关系数辨析及其在R语言中的实现[J].统计与信息论坛,2019,34(4):3-11.
[2] Gupta S.Point Biserial Correlation Coefficient and Its Generalization[J].Psychometrika,1960,25(4):393-408.
[3] 孔炜.上海市股票投资者的人格与投资行为的关系的研究[D].上海:华东师范大学,2005.
[4] 孙学明.初中学生语文偏误的统计学调查与研究[D].北京:首都师范大学,2004.
[5] Vincent L B,Michael A,Cox A.Interpretation of the point-biserial correlation coefficient in the context of a school examination[J].The Quantitative Methods for Psychology,2017,13(1):46-56.
[6] 曹盼盼,阎磊,顾玥,等.颈动脉内中膜厚度增加与老年慢性肾脏病患者发生认知功能障碍的相关性[J].中华实用诊断与治疗杂志,2019,33(2):124-127.
[7] 王美涵,陈培乐,潘晓映,等.基于相依区间值数据的EWMA FIMSE控制图[J].闽南师范大学学报(自然科学版),2021,34(3):1-7.
[8] 李城恩,潘晓映,王美涵,等.基于区间型数据计量的我国粮食产量研究[J].广西师范大学学报(自然科学版),2022,40(1):206-215.
[9] Cheng Y T,Yang C.An Approach of Stocks Substitution Strategy Using Fuzzy Interval Correlation Coefficient[J].Communications in Statistics-Simulation and Computation,2016,45(4):1187-1196.
[10] Yang C C.Correlation Coefficient Evaluation for the Fuzzy Interval Data[J].Journal of Business Research,2016,69(6):2138-2144.
[11] 杨志清.计数区间的模糊相关系数研究[J].统计与决策,2020,36(20):28-32.
[12] 王忠玉,吴柏林.一类模糊数据的相关系数研究[J].经济研究导刊,2015(2):248-251.
[13] Lev J.The Point Biserial Coefficient of Correlation[J].The Annals of Mathematical Statistics,1949,20(1):125-126.
[14] 秦志仁,董咪达.多系列相关系数的矩法估计[J].重庆师范大学学报(自然科学版),2004,21(1):10-13.
[15] 李金华.模糊数学方法与统计赋权[J].数量经济技术经济研究,2000(10):34-38.
[16] 汪顺玉,吴世银.评分员信度的多系列相关分析方法原理及运用[J].重庆邮电学院学报(社会科学版),2006(6):945-947.
Point biserial correlation coefficient and multiserial correlation coefficient of fuzzy interval
WANG Xinrui1,DOU Xinying1,YANG Zhiqing1,SHI Jianhua1,2,3,4
(1. School of Mathematics and Statistics,Minnan Normal University,Zhangzhou 363000,China;2. Fujian Key Laboratory of Granular Computing and Applications,Zhangzhou 363000,China;3. Fujian Key Laboratory ofData Science and Statistics,Zhangzhou 363000,China;4. Fujian Institute of Meteorological Big Data,Zhangzhou 363000,China)
In the study of the correlation between two random variables,the type of random variables has been expanded from the same type to the mixed type.However,under the condition of the combination of mixed random variables,the traditional correlation coefficient algorithm is not suitable for use when the data type presents a fuzzy interval pattern.Referring to the research results of traditional point biserial correlation coefficient,based on the mixed random variables combination of binary variables and multi-categorical variables with continuous random variables,the point biserial correlation coefficient and multiserial correlation coefficient of fuzzy interval are proposed.Afterwards,the effectiveness of this method is verified through Monte Carlo simulation and empirical analysis.
fuzzy interval;point biserial correlation coefficient;point biserial correlation coefficient of fuzzy interval;multiserial correlation coefficient of fuzzy interval
1007-9831(2022)11-0008-08
O21
A
10.3969/j.issn.1007-9831.2022.11.002
2022-03-15
国家社会科学基金项目(20XTJ003)
王鑫蕊(1997-),女,河南驻马店人,在读硕士研究生,从事应用统计分析研究.E-mail:857273302@qq.com
施建华(1977-),男,福建福清人,教授,博士,从事应用统计分析研究.E-mail:v0085@126. com

