代数模型在几何直观视角下的建构与运用——由一道中考试题的“一题一课”设计说起

姜晓翔

（浙江省湖州市南浔开发区实验学校）

罗增儒教授曾提出，解题即找出题目解的活动，解题教学是解题活动的教学.基于此，笔者认为，教师要让学生学会解题，先要提升自己解题教学的水平，尤其是在专题复习课中，优质的解题教学能让学生积累丰富的活动经验，并最终总结与归纳解题的通性、通法.卜以楼先生提出了生长理念，即找准生长点，选好生长路径，运用生长架构讲述思维登高的理性故事.基于生长理念下“六环”解题教学法探索研究，即“入题”“审题”“析题”“解题”“拓题”“理题”六个教学环节，将其应用于专题复习课等课型，能帮助学生获得更好的解题经验和思维方式，进而达成知识、方法、能力和思维等全方位的生长.通过对2018年中考浙江杭州卷第10题进行深入研究，并将该题作为教学素材中的母题，设计成一节“一题一课”形式的专题复习课，教学中渗透生长理念，并结合“六环”解题教学法探索出深刻的数学学习经验和思维方式.

一、复习目标

在知识层面上，复习巩固求三角形面积的常用方法，即直接法、等积法和等比法等；在方法层面上，探索并发现运用代数式、方程、不等式及函数等基本代数模型解决三角形面积问题的基本套路；在思想层面上，体会代数模型在几何直观视角下的建构与运用，并掌握数形结合、从特殊到一般、方程、数学建模及分类讨论等重要数学思想方法的运用和价值.最终达成知识生长、方法生长、能力生长及思维生长的目标.

二、学情分析

该专题复习课基于一道经典中考试题的解题教学，定位在学生学习完“相似三角形”内容后，作为章节专题复习课或中考第二轮专题复习课进行教学.此时，学生已经拥有上述提到的代数模型及相似三角形性质等必要的知识储备，并且具有初步的抽象能力、模型观念、几何直观、推理能力及运算能力等数学核心素养.学生正值亟待提升数学解题经验和思维品质之时，教师通过该复习课中的解题教学，以期能达成上述复习目标.

三、思考方向

1.试题呈现

题目 （2018年浙江·杭州卷）如图1，在△ABC中，点D在AB边上，DE∥BC，与边AC交于点E，连接BE，记△ADE，△BCE的面积分别为S1，S2，（ ）.

图1

（A）若2AD＞AB，则3S1＞2S2

（B）若2AD＞AB，则3S1＜2S2

（C）若2AD＜AB，则3S1＞2S2

（D）若2AD＜AB，则3S1＜2S2

2.试题思考

该试题是一道压轴选择题，借助三角形面积等常规知识考查代数建模思维在几何直观视角下的运用与转化.从试题的呈现形式来看，题干精炼，选择支匀称，图形简洁，是一道典型的几何与代数综合推理试题.然而，由于该题选择支中所设计的条件和结论均以不等关系呈现，对于学生而言相对陌生，较难理解和处理，难以入手，需通过有效转化进行具体分类与分析，具有较高的思维含量，故题目区分度也得以体现，是一道值得深入研究的好题.笔者运用基于生长理念下的“六环”解题教学法，将整个解题教学过程自然地串联成完整的一节生长型复习课，以求知识得到自然生长.

四、教学设计与评析

1.入题：设本源问题，搭双重铺垫

引例1 如图2，点D是△ABC的边AB上一点，且AD=2，AB=6，则△ADC与△ABC的面积比为（ ）.

图2

（A）1∶2 （B）1∶3

（C）1∶4 （D）1∶9

引例2 如图3，点D是△ABC的边AB上一点，且AD=2，AB=6，过点D作DE∥BC，交AC于点E，则△ADE与△ABC的面积比为（ ）.

图3

（A）1∶2 （B）1∶3

（C）1∶4 （D）1∶9

题后总结，如图4所示.

图4

【评析】以两道起点较低的练习题作为引例，降低了问题思维起点的难度，增加了入题的宽度，不仅起到了让全体学生都能参与的目的，还能引导学生去发现解决原题所必需的本源知识，即三角形的面积比问题.教师通过题后总结，进一步引导学生从引例提炼出与三角形面积之比相关的知识储备，并用如图4所示的思维导图直观呈现，进而为解决题目做好知识和思维上的双重铺垫.该环节既是对于“三角形的面积比问题”的一种知识生长，也为后续的各种其他层面的生长填石铺路.

2.审题：寻关键词句，破审题难点

题干关键词句：题目的大前提条件是“在△ABC中，DE∥BC，记△ADE，△BCE的面积分别为S1，S2”.（以上词句以划线形式进行标注和强调.）

选择支解读：四个选择支均为通过改变线段DE的位置，即当2AD＞AB或2AD＜AB时，来推理判断3S1与2S2的大小关系.

【评析】在整个解题中，审题环节尽量做到精准和精细.因此，在解题教学中，教师可以引导并督促学生养成良好的审题习惯，提高审题能力.上述审题环节中，教师让学生通过划关键词句的形式从题目中获取对问题解决有价值的重要信息，并找到原题中最难理解的审题困惑所在，结合图形和已知等相关信息精准地破解审题难点，从而为接下来的解题环节做好理解层面上的准备工作.

3.析题：悟几何直观，寻代数模型

（1）从关键词句思考.

由审题环节中所寻的题干关键词句“DE∥BC”，再结合引例的铺垫，不难联想到三角形的面积关系需要去分析相关线段的比，再结合“同（等）高不等底的三角形面积之比等于对应底之比”和“相似三角形的面积之比等于相似比的平方”的解题经验，进行三角形面积之间的转化.

（2）从选择支思考.

【评析】在审题环节，虽已确定该题的选择支是审题的难点，并进行了解读，但对于学生来说，这四个结论比较抽象和陌生，仍难以觅得解题思路.在析题过程中，教师从“关键词句”和“选择支”两个不同的思维起点进行引导，并激发学生的有效数学思考，进而体悟几何直观.与此同时，让学生体会到代数模型在解决此类问题中的重要作用，结合题中的相关条件去寻找突破口，进而解决问题.

4.解题：建代数模型，生自然解法

解题环节，即引导学生规范、完整地解答原题，并激发学生思考多元化解题思路的形成.基于上述各环节的思考与分析，有些解法即呼之欲出、自然生成，如特殊值法、缩放法、不等式性质法等.笔者预设了以下七种解题方法，其中方法1～方法4可以在解题教学时引导学生去发现并掌握，这也体现了方法的自然生长.

方法1：特殊值法.

对于选择题而言，特殊值法不失为一种有效、快捷的好方法.

由此推断，若2AD＞AB时，3S1与2S2的大小无法判断，故选项A和选项B均不正确.

该方法依托的代数模型是代数式求值问题.

方法2：合情推理法.

该题虽然是选择题，但用特殊值法也并不容易得到正确答案，真正容易想到的自然解法是合情推理法，即借助临界情况，通过位置的变化观察与推理3S1与2S2的大小关系.

当向上平移DE，即2AD＜AB时，S1将变小，S2将变大，则3S1＜2S2始终成立；

而当向下平移DE，即2AD＞AB时，S1将变大，S2将变小，此时3S1与2S2的大小无法确定.

故选项D正确.

该方法实质上是借助函数增减性来进行合情推理.

方法3：适度缩放法.

该题涉及不等关系，解决不等关系的通法是通过对关键的量进行适度缩放，进而转化为所需的结果.

故选项D正确.

该方法借助不等式模型，确定临界位置，适度缩放转化来解决问题.

方法4：不等式性质法.

利用不等式的基本性质往往可以巧妙地解决一些关于不等关系的推理问题.

同方法1，考虑临界情况，当2AD=AB时，AE=EC，S1+S△BDE=S2.

当2AD＜AB时，AD＜DB，AE＜EC，所以S1+S△BDE＜ S2，S1＜ S△BDE，S1＜ S2.所以3S1+S△BDE＜ 2S2+S△BDE，即3S1＜ 2S2.

当2AD＞AB时，AD＞DB，AE＞EC，所以S1+S△BDE＞ S2，S1＞ S△BDE，S2＞ S△BDE.所以 2S1+2S△BDE＞2S2. 所以4S1＞ 2S2，即2S1＞ S2，此时3S1与2S2的大小无法确定.

故选项D正确.

该方法借助不等式模型，利用不等式基本性质进行适度缩放转化来解决问题.

方法5：基准构造法.

对于几何问题中不等关系的推理，可以构造一个基准，通过分析不等式两边与该基准的大小关系进行推理.

图5

同理，当2AD＞AB时，在AB的延长线上截取DF=DA，过点F作FG∥BC，交AC的延长线于点G，连接FE，如图6所示.

图6

所以此时3S1与2S2的大小无法确定.

故选项D正确.

该方法表面上是几何层面的构造，但实质还是依托不等式模型的传递性来转化处理，进而解决问题.

方法6：参数面积法.

关于三角形的面积问题，学生也容易想到三角形的面积公式，然而题中没有具体数据，故可以根据选择支的条件设好参数，利用参数面积法求解.

如图7，过点D作DF⊥AC于点F，过点B作BG⊥AC于点G，

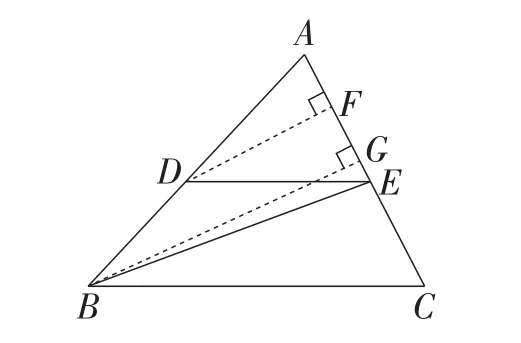
图7

故选项D正确.

该方法利用代数式的比值来解决代数式的大小比较问题.

方法7：构造函数法.

基于选择支的四个结论，上述方法都以“2AD=AB”为临界情况，如果逆向思考，也可以以“3S1=2S2”为临界情况，用设参数和借助函数模型解决问题.

即n1≈-2.4，n2≈1.1.（为了便于分析，根的值用近似值代替.）

因为y是关于n的二次函数，抛物线开口向上，故由图象可知：当n=1.1时，y=0；当0＜n＜1.1时，y＜0；当n＞1.1时，y＞0.

由此可判断只有选项D正确.

该方法通过建构函数模型，借助方程思想解决问题.

【评析】上述解题环节展示了多种不同思路的解题方法，在拓宽学生思维的同时揭示了问题的本质.从知识层面来看，选择支中研究的“面积关系”实质上就是“线段关系”的一种函数表征，此乃知识生长.从方法层面来看，上述方法均反映了代数模型在几何直观视角下的建构与运用，方法1～方法6单纯只是为了得出结果，解决原问题，而方法7将几何问题通过数形结合转化为通过作差比较大小，最终利用函数性质来解决，方法进一步得到生长.从能力层面来看，无论何种方法，通法就是确定临界位置，适度缩放转化.教师通过解题环节的组织，让学生探究和自然生长出多种解题方法，并最终体悟出所有方法的本质，进而提炼出解题通法，最终促进学生能力的生长.

解题教学源于解题和解题研究，教学效果取决于教师解题教学经验的积累.笔者预设的以上七种解题方法，相较而言，前四种方法基于初中学生的能力自然生成，而后三种方法带有一定的技巧性及高中阶段的参数理念，可以作为教师的解题研究.站得高才能看得远.在解题教学时，教师研究的高度需要更高一些，才能让学生的能力提升更快一些.

5.拓题：依托元问题，促思维生长

教师预设的元问题1：不改变原图形，将原题中的部分条件改掉，试编制一个新的问题.

以下生长问题均为笔者所预设，教师在教学中应尽量引导学生编制新问题.

教师预设的元问题2：在原题的基础上，适当增加条件，试编制一个新问题.

图8

生长问题6：如图9，在原题的条件下，F是线段DE上任意一点，连接FB和FC，分别记△ADE，△BFD，△CFE的面积为a，b，c，求△BFC的面积（用含a，b，c的代数式表示）.

图9

【评析】在拓题环节，通过巧妙设计两个元问题，充分激活了学生的思维.如果教师能加以精准引导，学生高阶思维中的创新思维能力和批判性思维能力将得以彰显.教师应该适时引导学生进行归类与整理，培养学生的整体性思维和结构化思维，使学生的思维能力得到进一步升华和生长，使深度思考得以落实.

6.理题：画思维导图，得解题套路

到了结课之时，该题的学习暂告一段落，要引导学生进行课堂内容的整理、归纳与提炼，得如图10所示的思维导图.知识生长：三角形面积关系转化成线段关系.方法生长：不同的代数模型可以生长出不同的方法，关键在于择优和通性通法.思维与能力生长：数学核心素养和数学思想方法的渗透和掌握.

图10 代数模型在几何直观视角下的建构与运用

【评析】成功的解题教学既要有生长，又要有回归与整理.理题，即反思与提炼环节，是解题的归宿.解题后要养成反思、提炼的习惯，回顾问题的深层次结构，从而提炼和积累重要的解题经验和思维方式.在“结课”环节，结合思维导图的形式加以表征，既能使学生抓住解题重点、方法和步骤，又能厘清各个环节之间的逻辑联系，更全面、直观地感受该题的解题精髓与脉络，为今后解题方法的触类旁通及灵活运用打下坚实的基础.

五、结束语

教学有法，教无定法，贵在得法.数学复习课也是如此，它没有一个固定的模式，但有一定的规律需要遵循.一节好的复习课，不仅要精心选择与打磨例题，还要对例题的教学以及促进学生各方面生长的过程进行精心设计.本节基于生长理念的“六环”解题教学法复习课，将一道典型的中考试题作为教学素材的母题，通过用“六环”进行精心设计，引导学生达成教师预设的复习目标的同时，更让学生初步理解和掌握代数模型在几何直观视角下的建构与运用.相信，学生不仅在知识层面和方法层面上有质的提升，还能在能力层面与思维层面上延续生长，并对今后的数学学习起到可持续性的数学育人作用.