基于灰色关联度和靶心距的多属性决策模型及其应用
刘解放,杨蓉蓉
(天津职业技术师范大学经济与管理学院,天津 300222)
在实际生产生活中,人们经常会面对决策问题,决策问题大都带有多属性的特征,因此多属性决策问题求解方法成为了研究的热点[1-12]。求解多属性决策问题,经常使用TOPSIS(technique for order preference)方法,该方法利用备择方案与理想方案之间的距离作为依据,距离越小,则说明备择方案与理想方案越接近,备择方案越好。近年来,随着研究的深入,有学者构造了负理想方案,决策时同时考虑备择方案与负理想方案之间的距离,距离越大,则说明备择方案与理想方案越接近,备择方案越优,从而可以同时考虑备择方案与正负理想方案之间的距离,该方法更加有效地利用了备择方案隐含的有效信息。但是,TOPSIS方法仅从距离的角度考虑决策方案的优劣,无法体现备择方案与理想方案之间的几何相似性。
灰色关联算法从序列的几何相似程度上考虑备择方案的优劣,备择方案与理想方案在几何上越相似,灰色关联度越大,则备择方案越优。蒋诗泉等[13]基于矩估计理论构建了一般灰数的灰色关联决策模型;刘勇等[14]针对属性值为区间直觉模糊数且属性权重未知的一类决策问题,构建了一种动态区间直觉模糊数多属性决策方法;刘中侠等[15]针对指标值为区间灰数且权重属性部分已知、部分未知的决策问题,提出一种新的决策方法;蒋诗泉等[16]构建了新的灰色关联度公式;邓聚龙教授[17]提出灰靶决策方法,构建了一个球形灰靶,以最优方案为靶心,以靶心距的大小作为衡量方案好坏的依据,近年来得到了广泛的应用。刘小弟等[18]构建了基于多维关联抽样的区间数灰靶决策模型;罗党[19]考虑实际决策环境的不确定性和复杂性,提出一种新的灰靶决策模型;郭三党等[20]考虑了决策者的心理行为,提出一种基于后悔理论的多目标灰靶决策方法。现有的研究大都从距离的角度或者几何相似性的角度考虑备择方案的优劣,针对方案信息为区间数的情形,从这个方面考虑的文献还比较少见。基于此,本文提出了基于灰色关联度和靶心距的多属性决策模型,给出了模型的建模步骤和计算方法,通过实例验证了该方法的有效性和实用性。
1 基于灰色关联度的多属性决策模型
1.1 区间数的距离与区间数的加权关联度
定义1设A=[aL,aU],aL≤aU,B=[bL,bU],bL≤bU,为2个区间数,称D(a,b)为区间数A与B之间的距离。
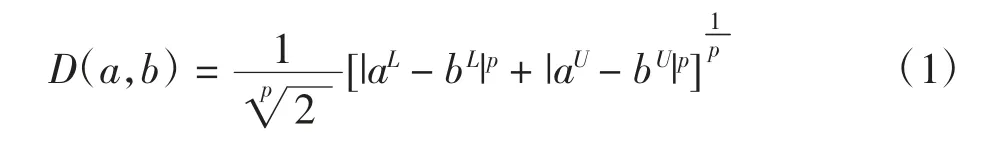
定义2设系统行为区间数序列为

系统行为区间数序列X(0),X(1),…,X(m)的权重向量为(ω0,ω1,…,ωm),称ξ0i(k)为X(0)与X(i)在k时刻的加权关联系数。
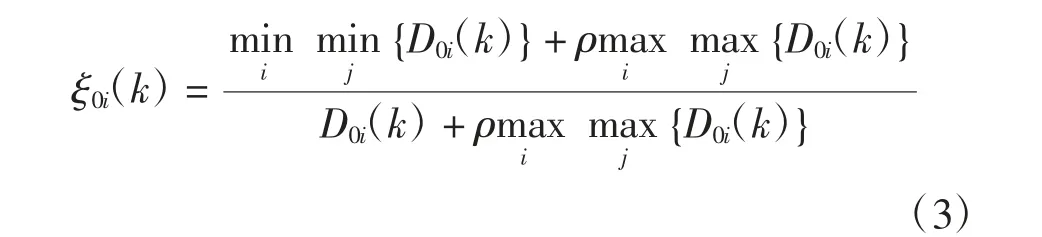
式中:D0i(k)为(x0L(k),x0U(k))与(xiL(k),xiU(k))之间的加权距离;ρ为分辨系数,ρ∈[0,1]。
定义3称γ0i为区间数X(0)与X(i)的加权灰色关联度。

1.2 基于区间数的多指标灰色关联决策模型
假设要评价的对象为A1,A2,…,Am,评价指标为C1,C2,…,Cn,则称决策方案集为{A1,A2,…,Am},评价指标集为{C1,C2,…,Cn};方案Ai对指标Cj的属性值为区间数[xijL,xijU],i=(1,…,m),j=(1,…,n)。则评价方案集对评价指标集的决策矩阵为

1.2.1 决策矩阵的规范化处理
为了消除指标的量纲,对数据进行规范化处理。
定义4设X=([xL(1),xU(1)],[xL(2),xU(2)],…,[xL(n),xU(n)])为区间数向量,则称‖X‖max=max(|xL(1)|,|xU(1)|,|xL(2)|,|xU(2)|,…,|xL(n)|,|xU(n)|)为区间数向量的极大范数;称‖X‖min=min|xL(1)|,|xU(1)|,|xL(2)|,|xU(2)|,…,|xL(n)|,|xU(n)|)为区间数向量的极小范数;则对区间数指标做如下规范化处理
若Aj为效益型指标,则
若Aj为成本型指标,则
从而得到规范化决策矩阵

很明显,rijL,rijU∈[0,1],i=(1,…,m),j=(1,…,n)。
1.2.2 灰色关联决策分析
经过规范化处理的决策矩阵X,已经消除了量纲,且均已经转化为效益型的变量,即“越大越好”。因此,只需选取区间数中最大的变量作为理想变量,选取区间数中最小的变量作为负理想变量。
定义5设ri0j=[ri0jL,ri0jU]=[max(rijL,1≤i≤m),max(rijU,1≤i≤m)],称
S+=ri0j={[ri01L,ri01U],[ri02L,ri02U],…,[ri0nL,ri0nU]}为区间数正理想方案。
定义6设ri0j=[ri0jL,ri0jU]=[min(rijL,1≤i≤m),min(rijU,1≤i≤m)],称
S-=ri0j={[ri01L,ri01U],[ri02L,ri02U],…,[ri0nL,ri0nU]}为区间数负理想方案。
由式(3)可计算得到,方案Ai与S+关于指标Cj的区间数加权关联系数ξij+(k),进而求得区间数X(0)与S+的加权灰色关联方案Ai与S-关于指标Cj的区间数加权关联系数ξij-(k),进而求得区间数X(0)与S-的加权灰色关联度为
评价方案的优劣,不仅要考虑备择方案与正理想方案的接近程度,还要考虑备择方案与负理想方案的远离程度。假设设计方案Ai以关联度pi从属于S+,那么,Ai即以1-pi从属于S-。定义求解综合关联度pi的方法为
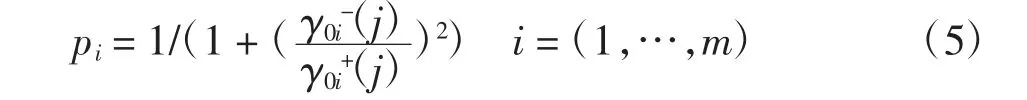
pi越大,设计方案Ai越好。
2 基于正负靶心的灰靶决策模型
灰靶决策的基本思想是在一组序列中,找出最靠近目标值的序列,称为靶心,各序列与靶心的距离称为靶心距,靶心距越小,则该序列越接近目标值。依据该思想可以将最劣方案定义为负靶心,将各方案与负靶心的距离定义为负靶心距,同时考虑正负靶心距对方案进行决策分析。
定义7设xj+=max{(xijL+xijU)/2|1≤i≤m|}(j=1,2,…,n),称Xj+={x1+,x2+,…,xn+}={[x1L++x1U+],[x2L++x2U+],…,[xnL++xnU+]}为正靶心。
定义8设xj-=min{(xijL+xijU)/2|1≤i≤m|}(j=1,2,…,n),称
Xj-={x1-,x2-,…,xn-}={[x1L-+x1U-],[x2L-+x2U-],…,[xnL-+xnU-]}为负靶心。
记方案A(i)=([xiL(1),xiU(1)],[xiL(2),xiU(2)],…,[xiL(n),xiU(n)])的正靶心距为

负靶心距为
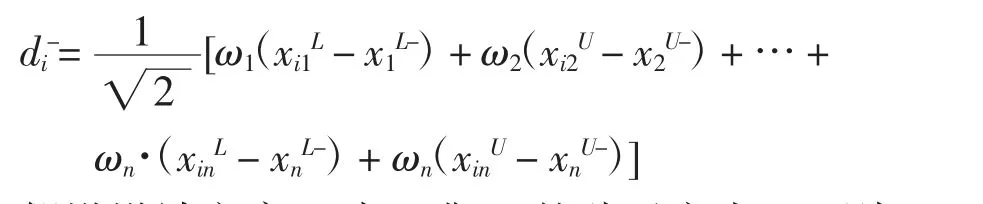
假设设计方案Ai与正靶心的贴近度为qi,则Ai与负靶心的贴近度为1-qi。为了确定综合贴近度qi,定义如下求解qi,为

qi越大,设计方案Ai越好。
3 综合考虑灰色关联度和靶心距的决策模型
灰色关联度可以从几何形状上描述方案Ai与理想方案的相似性,而靶心距可以从距离尺度上描述方案Ai与靶心的接近性,二者互相补充,可以更好地描述方案Ai的优劣,本文将关联度和靶心距相结合,构造出一种新的多属性决策模型,具体算法如下:
(1)确定方案集{A1,A2,…,Am},评价指标集{C1,C2,…,Cn}以及各指标的权重向量(ω0,ω1,…,ωm),求得方案集A对指标集C的决策矩阵X。
(2)对决策矩阵X进行规范化处理,结合权重,得到规范化决策矩阵R。
(3)确定正负理想方案S+和S-正负靶心Xj+、Xj-。
(4)计算备择方案Ai与正理想方案的关联度γi+,与负理想方案的关联度γi-。
(5)计算备择方案与正靶心的距离di+,与负靶心的距离di-。
(6)计算Ai的综合关联度pi,求得综合贴近度qi。
(7)计算方案Ai的综合优属度fi

其中,α反映了决策者对于形状相似性的偏爱程度。
(8)按照综合优属度的大小对方案进行排序。综合优属度越大,方案越优;综合优属度越小,方案越劣。
4 应用举例
某投资银行欲对本市4家企业A1、A2、A3、A4进行投资,为了对不同的企业进行评估,选取4项指标进行投资决策。指标C1为投资净产值率,C2为投资利税率,C3为内部收益率,C4为环境污染程度。
区间数决策矩阵如表1所示。其中,指标A1、A2、A3为效益型指标,A4为成本型指标。各指标的权重设为(0.2,0.2,0.35,0.25)。

表1 区间数决策矩阵
(1)根据问题描述,可得方案集A={A1,A2,A3,A4},指标集C={C1,C2,C3,C4},方案集A对指标集C的决策矩阵X

(2)计算加权规范化决策矩阵R

(3)分别确定正负理想方案S+、S-

(4)计算方案Ai与正理想方案的关联度γi+,Ai与负理想方案的关联度γi-,得到方案Ai与正理想方案的关联系数矩阵

因此,方案Ai与正理想方案的关联度γi+=[0.498 7,0.696 4,0.716 9,0.583 2]。
方案Ai与负理想方案的关联系数矩阵

那么,方案Ai与负理想方案的关联度γi-=[0.7052,0.685 2,0.579 0,0.547 9]。
(5)确定正负靶心Xj+、Xj-

(6)计算方案Ai与正靶心的距离di+,与负靶心的距离di-

根据式(5),得到综合关联度pi=[0.333 4,0.508 0,0.605 2,0.531 2];根据式(6),得到综合贴近度qi=[0.173 4,0.539 4,0.645 8,0.493 0]。
(7)计算方案Ai的综合优属度fi=αpi+(1-α)qi,fi=[0.253 4,0.523 7,0.625 5,0.512 1]
其中,为了平衡考虑决策者对于几何形状相似性和距离接近相似性的偏好程度,此处取α=0.5。
(8)按照综合优属度的大小对方案进行排序,从计算结果可以得到:f3>f2>f4>f1,则A3≻A2≻A4≻A1,那么方案A3为最优方案。若α取不同的值,会得到不同的排序结果,不同偏好下排序结果对比如表2所示。

表2 不同偏好下排序结果对比
5 结语
针对指标值为区间数的多属性决策问题,建立了基于灰色关联度和靶心距的决策模型,首先计算正负理想方案和正负靶心,然后分别计算方案Ai的综合优属度和综合贴近度,最终计算得到方案Ai的综合优属度,按照综合优属度的大小对方案进行排序,综合优属度越大,方案越优;综合优属度越小,方案越劣。新模型综合考虑了备择方案和理想方案在几何形状和距离上的接近性,可以有效弥补灰色关联决策模型和灰靶决策模型的不足。该方法的物理意义明确,操作简便,分析问题更加客观,为指标值为区间数的多属性决策问题的解决提供了一种新的方法。

