考虑折射影响的摄影测量法土工三轴模型精度分析

唐怡怀， 黄少染， 牟春梅,2

(1. 桂林理工大学土木与建筑工程学院，广西 桂林 541004; 2. 广西岩土力学与工程重点实验室，广西 桂林 541004)

0 引 言

常规三轴试验由于试验装置及方法的局限，只能获取土样整体的平均变形[1]，无法详尽地反映土样的变形特征，且难以用于非饱和土体的变形测量[2]。针对以上问题，国内外学者将数字图像测量技术用于土工三轴试验中[3]，通过图像测量手段实现对三轴试验过程中土样的变形测量。基于图像测量的三轴试验方法不受土样必须完全饱和的条件限制，还可以获取土样的局部化应变。目前常见的技术手段有数字图像分析技术(digital image analysis technology，DIA)[4-5]、数字图像相关技术 (digital image correlation technology，DIC)[6-7]、邵龙潭研究团队的三轴试样全表面变形数字图像测量系统[8-10]以及Li 等[11-15]的摄影测量技术。基于DIA技术的三轴试验是通过识别图像中土样的边缘轮廓，获取土样轴向变形与径向变形。该方法假设条件在实际情况中难以满足，并且必须准确知晓压力室及土样与相机的相对方位[15]，实际的测量精度难以达到预期水准。基于2D-DIC技术的三轴试验通过关联处理土样变形前后的图像，得到不同图像中同名点的变化实现土样表面局部化变形测量。但此方法仅局限于土样局部化平面测量，无法实现对土样的全表面立体观测。随着图像技术的发展，在2D-DIC技术的基础上，结合双目立体视觉原理形成了3DDIC技术[16]，运用双相机从不同空间位置同时观测目标物表面一点，根据其在两幅同时刻的图像中像素点以及双相机的内外参数[17-18]，确定其在空间中的三维坐标。然而，由于3D-DIC技术不能有效解决光线在压力室和水的折射问题，难以应用于土工三轴试验中。全表面变形数字图像测量系统的三轴试验利用亚像素点检测原理，追踪土样表面各角点的位置变化，实现土样表面任意时刻的应变场绘制。然而此方法需将圆筒状压力室改制成平面板状从而不适用于常规三轴试验，并且改制后的平面板状压力室仍无法消除压力室与水产生的折射影响。摄影测量法的三轴试验一定程度克服了上述图像测量方法的局限性，无需对常规三轴试验仪器进行任何改造，可在常规三轴试验基础上进行。该方法基于近景摄影测量原理，手持一部普通数码相机（单镜头）采集土样全表面二维图像，随后利用多视角下的三轴土样图像重构土样的三维空间形态，实现对三轴土样的轴向应变、径向应变、局部应变及体变的全过程测量。此外，摄影测量法建立的折射修正模型，考虑了压力室受围压作用下出现鼓胀变形导致折射界面的改变对折射修正结果产生的影响，可实现高精度的折射修正。

本文将近景摄影测量法用于土工三轴试验，选用表面附有编码点的硬质圆柱作为三轴模型。通过基于摄影测量的三轴模拟试验，建立折射修正模型对折射误差进行校正，获取空气中、压力室并注水及折射修正后三种情况下模型轴向值与径向值。将以上测量值与空气中三轴模型游标卡尺测量值进行比较，评估在三轴试验中摄影测量轴向与径向的测量精度。同时比较三轴模型折射修正前后的形态异同，探究了折射对三轴模型成像的影响及轴向与径向成像产生差异的原因。最后，为进一步提高摄影测量法三轴土样变形测量的精度提供一定借鉴。

1 摄影测量法的基本原理

摄影测量法是基于近景摄影测量的原理，利用相机从至少两个不同方位拍摄被测目标点的图像，通过软件识别不同图像中的同名点，获取不同图像中同名点的图像像素坐标，根据不同图像的视觉交汇，确定该目标点的唯一空间点。具体的方法[11-12]如下：以常规三轴试验为基础，在加载框架、压力室外表面及橡皮膜上张贴标记点RAD（ringed automatically detected）编码点（详见图 1），每个编码点都赋有唯一的序列编号，可被PhotoModelerScanner图像处理软件自动识别；利用校正表和软件检校模块校正测试镜头，手持校正后的单镜头相机对压力室内部被摄物体进行环绕式拍摄，将获取的图像分组输入PhotoModelerScanner图像处理软件中进行识别与匹配；运用摄影测量分析技术确定拍摄相机的方位以及压力室的形态与位置，随后利用光线追踪技术处理多重介质（水、有机玻璃压力室、空气）引起的折射问题，并运用最小二乘法确定被摄物体表面编码点的最终三维坐标，重建加载框架、压力室和被摄物体的3D坐标模型，进而根据编码点位置的变化计算被摄物体的体积变化，实现被摄物体的局部与整体变形测量。

在三轴试验摄影测量过程中，成像光线在多重介质的交界处折射产生偏移。为确定光线折射后的方向，在折射界面处运用折射定理即可根据入射光的入射角计算出光线折射角。但是在三轴试验过程中，有机玻璃压力室受围压作用下发生蠕变呈现微鼓胀形态，此时的折射界面与标准圆柱状压力室的折射界面不符。因此，如何拟合与压力室实际形态相吻合的函数界面对恢复光线传播路径至关重要。针对上述问题，摄影测量法通过建立基于光线追踪的折射修正模型校正折射误差，获取趋于被摄物体原型的三维模型。折射修正模型是基于压力室玻璃材质均匀的假设前提下进行，其过程主要分成两部分，一是有机玻璃压力室形态和位置的确定，二是编码点坐标的修正。圆柱形压力室的形态和位置由含有9个未知参数的数学模型表征，模型参数根据压力室表面编码点的三维点云坐标使用最小二乘法求得最优的参数组合，拟合与实际相吻合的折射界面。编码点坐标的修正即利用多条光线追踪技术和最小二乘法消除折射对图像测量结果的影响。光线追踪利用光线的可逆性，通过像点逆向追踪成像光线的传播路径确定物点坐标[19-20]，但由于外部因素的不可控性，多条逆向光线难以按照理想状态收敛成一点。为此，运用最小二乘法确定逆向光线最终交汇点，实现对编码点坐标的准确定位。本文采用Li[11-12]所提出的基于光线追踪的折射修正模型，并在此基础上，将上述折射处理过程集合成程序，通过试验分析摄影测量法建立的折射修正模型处理折射问题的准确性。

2 试验方案及试验数据获取

2.1 试验方案

本次试验选择一个形态规则的硬质圆柱作为三轴土样模型（以下称为三轴模型），模拟三轴土样在空气中以及充水后压力室内部的状态。分别采用精度为0.02 mm的游标卡尺和摄影测量法对空气中和压力室内部的三轴模型进行测量，将两种方法所得轴向高度H和径向直径D进行对比分析。

2.2 试验准备

2.2.1 模型标记点的设置

从PhotoModelerScanner图像处理软件中导出RAD编码点并打印在A4纸上，随后将若干RAD编码点粘贴在三轴模型表面（呈9行×15列分布，共135个编码点）。另外对每行、列进行编号，以便于后续试验的图像采集及结果分析，如图1所示。

图1 三轴模型标记点的设置

2.2.2 试验系统的建立

在摄影空间内定义统一的世界坐标系与模型比例对重构三维模型具有十分重要意义，可实现不同重构模型之间的变形对比。为此，在三轴仪两侧加载框架上分别粘贴一列编码点，世界坐标系通过加载框架上编码点定义，构建以水平方向为X轴、竖直方向为Y轴的世界坐标系O-XYZ，模型比例通过游标卡尺测得加载架上点间距确定。随后在压力室外表面粘贴四行和四列编码点，并将附有编码点的三轴模型置于压力室中心，试验系统设置如图2所示。

图2 试验系统的设置

2.2.3 相机校正

本次试验采用手机(f/2.2光圈，800万像素5镜式镜头)进行摄影测量。同时选用手机具备：1）高分辨率、防抖、轻巧等特点，适用于室内开展图像采集；2）其后置镜头为单摄像镜头，适用于摄影测量领域。然而，普通相机由于内方位元素未知以及镜头存在光学畸变，无法直接用于摄影测量。为了获取相机内方位元素以及多种畸变参数，首先运用测试镜头环绕拍摄等距网格校正表，共12幅图像，然后通过PhotoModelerScanner图像处理软件的检校模块完成上述参数的求解[21]。等距校正表及手机拍摄方位如图3所示，相机校正结果详见表1。

图3 等距校正表及手机拍摄方位图

表1 手机校正前后参数

从表1可见，除相机的横向像素M、纵向像素N以及传感器尺寸Fy外，其余参数与相机的标定参数皆存在明显的差异。K1、K2表示径向畸变参数，P1和P2表示切向畸变参数，在校正前相机的畸变参数均不为0，说明原图像存在一定程度的图像畸变，通过上述畸变参数可将呈现桶状畸变或枕状畸变的图像恢复正常。相机的校正质量由像点的残差值决定，通过软件检校模块处理12幅图像获取校正表的空间点云图，见图3(b)。当最大像素残差值在1.0 pixel及以下时，表明相机校正成功。

2.3 试验数据的获取

利用游标卡尺对三轴模型附有编码点区域内的径向直径、轴向高度进行测量，按照编号统计相应测量结果。随后进行系统设置并在三轴仪底座上安装三轴模型，手持校正后的相机拍摄获取空气中、安装压力室并注水两种情况下的三轴模型图像。具体操作步骤如下：1）首先正对附有编码点的荷载架从不同方位拍摄5～6幅图像，随后环绕三轴模型拍摄25～35幅图像。2）拍摄完成后，安装压力室并注满水，以相同的方式环绕压力室拍摄，获取包含加载框架编码点、压力室外壁编码点及模型表面编码点的图像，一次拍摄50幅图像左右。此外，相邻图像间的重叠率应大于70%，三轴模型表面每个编码点至少在5幅图像上出现。

运用PhotoModelerScanner图像处理软件对三轴模型图像进行分组处理，输出所有相机光心的三维坐标、压力室外壁编码点的三维坐标、空气中三轴模型的三维坐标以及压力室内部三轴模型的三维坐标等信息。根据相机光心、压力室表面编码点的三维坐标与压力室内部三轴模型的三维坐标建立基于光线追踪的折射修正模型，消除折射引起的放大效应，确定三轴模型表面编码点的真实三维坐标。为便于执行折射修正过程，在Matlab软件编写了相应折射修正的程序，实现折射误差的快速修正。

将三轴模型在空气中以及压力室内修正前后的编码点三维坐标按行列编号进行分类统计。轴向上根据三轴模型表面首行与末行的两RAD编码点三维坐标z值之差确定，而径向上提取模型RAD编码点的三维坐标中x、y值，通过拟合圆函数获取径向直径，并计算平均值。

3 试验结果分析

试验结果可分为三部分，一是评估空气中进行摄影测量的准确性，二是评估模拟试验中摄影测量的准确性，三是折射修正前后试验结果对比分析。

3.1 空气中的准确性验证

利用卡尺和摄影测量法对编码点间距进行对比测量，初步评估摄影测量法的准确性。如图4所示，将分辨率为0.02 mm的游标卡尺放在印有编码点的A4纸上，测量编码点（编号1～10）两两之间的距离；使用经校正后的手机从不同方位拍摄，共6幅图像，然后运用PhotoModelerScanner图像处理软件对图像进行处理，获取编号1～10相邻两编码点的间距值，两种方法测量结果见表2。

图4 空气中的精度验证试验

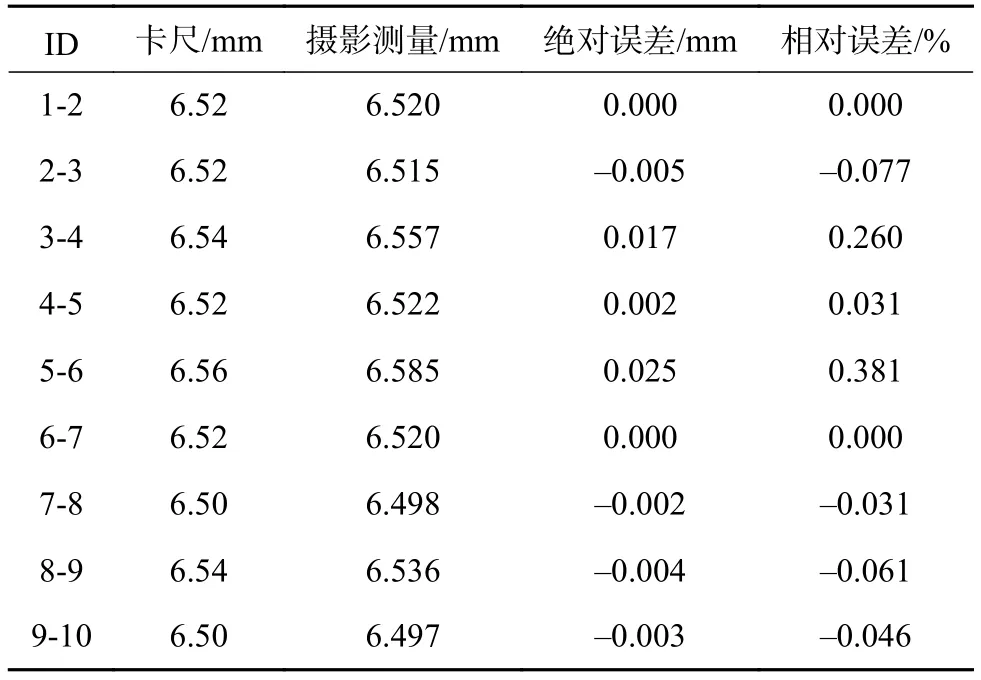
表2 游标卡尺和摄影测量法分析结果对比

从表2可见，以卡尺测量结果作为点间距的“基准值”，摄影测量结果与卡尺测量结果基本一致，点间距测量值的最大绝对误差和最大相对误差分别为0.025 mm和0.381%。在9个测量值中，7个测量值的绝对误差值小于0.01 mm。由此表明，摄影测量法用于空气中具有较高的测量精度，将其用于变形测量具有一定可行性。

3.2 三轴试验的模拟试验

在三轴试验摄影测量过程中，由于有机玻璃压力室和水所产生的折射会引起摄影测量结果的失准，故分析时需要考虑折射对测量结果产生的影响，其测量精度需要进一步分析。通过基于摄影测量的三轴模拟试验，分别获取空气中三轴模型的尺寸测量值（H空气、D空气）和注水压力室内三轴模型的尺寸测量值（H修正、D修正），将以上结果与空气中三轴模型的游标卡尺测量值（H卡尺、D卡尺）进行比较，相关结果见表3、表4。

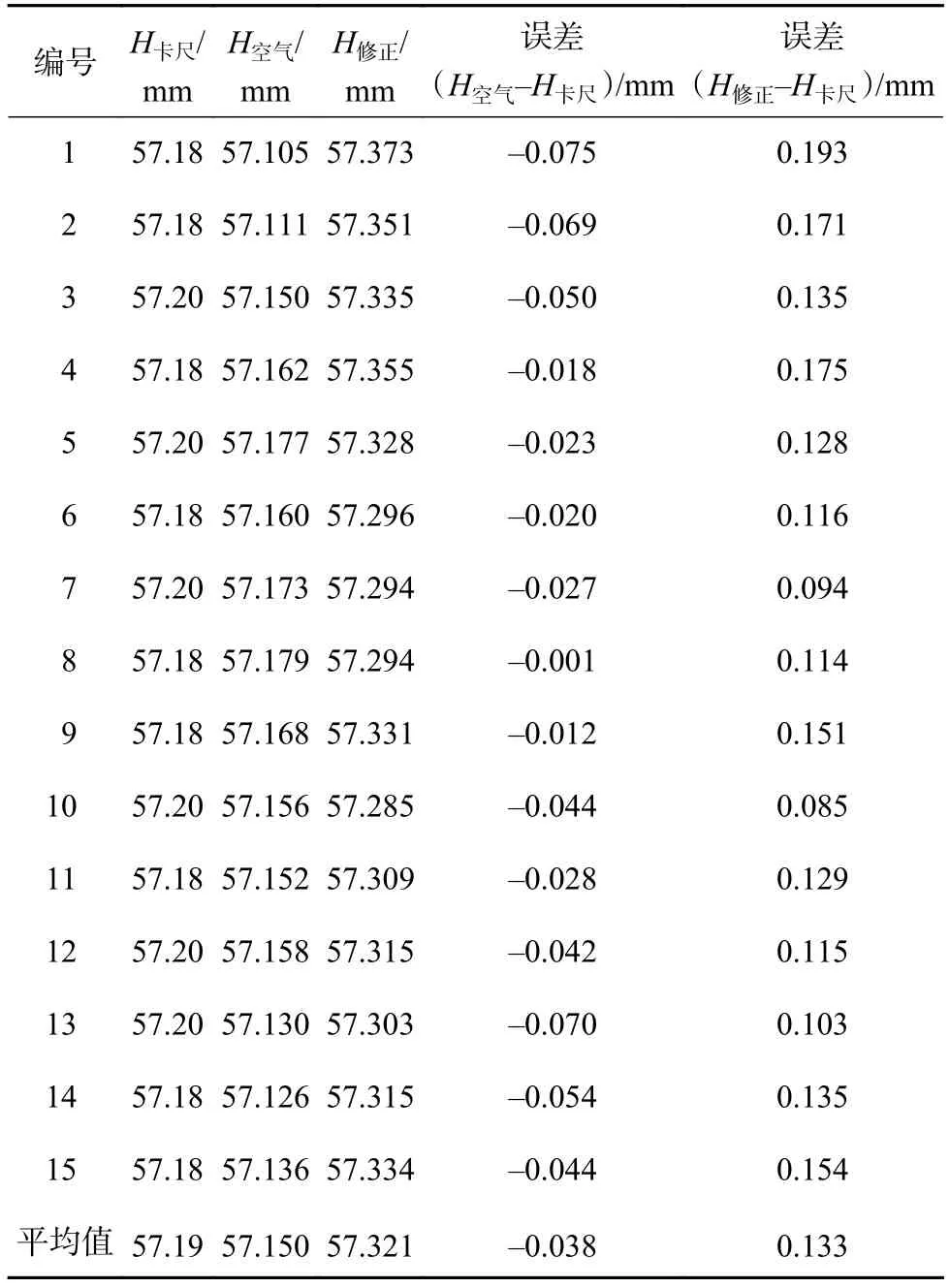
表3 三轴模型轴向高度测量结果分析

表4 三轴模型平均径向直径测量结果

根据表3三轴模型轴向高度的测量结果分析，以卡尺测量H卡尺值作为轴向“基准值”，在空气中的摄影测量轴向测量值与卡尺轴向测量值相近，其中最大误差为-0.075 mm，最小误差为-0.001 mm，平均误差为-0.038 mm；而修正后的摄影测量轴向测量值H修正与轴向“基准值”H卡尺存在明显差异，最大误差为 0.193 mm，最小误差为 0.085 mm，平均误差为0.133 mm，相较之下H修正值的误差比H空气值大。同时结合表2可知，同是在空气中进行摄影测量，三轴模拟试验中摄影测量的准确性却不如在空气中精度验证试验中的表现，空气中三轴模型高度的测量误差大于点间距的测量误差。这是因为在处理空气中三轴模型图像时，各点坐标通过识别不同图像中同名点确定，编码点的残差值并不完全小于1.0，故获取的编码点坐标存在一定的偏差；而在空气中精度验证试验中，相邻图像间的重叠率达到100%，编码点识别的准确性相对更高，故得到点的位置坐标更准确。

根据表4三轴模型径向平均直径的测量结果分析，以卡尺测量D卡尺值作为径向“基准值”，D空气值的误差为-0.005 mm，而D修正值的误差为 0.201 mm，在径向上折射修正后的测量误差明显大于摄影测量空气中的测量误差。造成径向修正结果误差较大的原因可能有两个：一是人为因素造成行向编码点不完全处于一条直线上，从而影响了此次圆函数的拟合；二是摄影测量在折射修正过程中目标点的定位存在偏差所致。三轴模型上每个编码点至少在5幅图像上出现，理论上通过不同图像产生的逆向光线形成的视觉交汇即为该编码点的坐标位置，然而由于外部因素影响，光线无法按照理想状态汇聚成一点。因此，运用最小二乘法解决光线无法交汇确定物点的问题，其基本原理是：假设物点为光源，那么所有光线都由物点发散，此时物点与所有光线存在最短距离即物点至逆向光线的距离di的平方和最小。在处理过程中，当di值大于临界值0.15 mm时，即认为光线偏离距离较大，确定的物点误差较大，应剔除对应的光线，随后将剩余光线进行重新计算。

图5展示了其中5个修正点所使用的图像数量及具体的di值。从图上可见，折射修正过程使用的图像数量最少有8幅，最多有11幅，获得的编码点坐标将更加精确。同时，此次抽选5个点的di值绝大部分处在0.04 mm以内，表明通过最小二乘法确定编码点的最终位置相对准确。

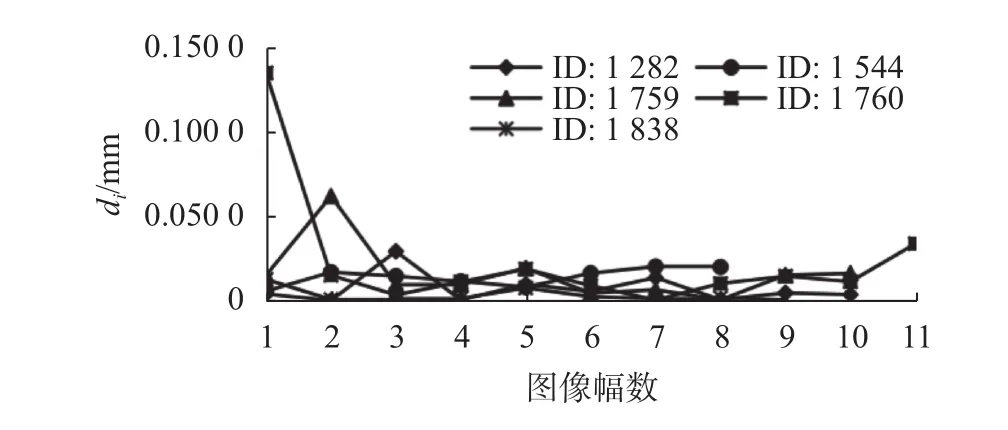
图5 模型上5个修正点所用的图像数量以及具体的di值

3.3 折射修正前后对比分析

为了进一步分析折射影响产生的放大现象，将折射修正前后三轴模型的形态绘制在同一图形上，并根据点云坐标获取折射修正前后的径向测量平均值与轴向测量平均值，如图6所示。同时，将修正前后的三轴模型轴向高度（H未修正、H修正）与卡尺测量值（H卡尺）进行比较，如图7所示。

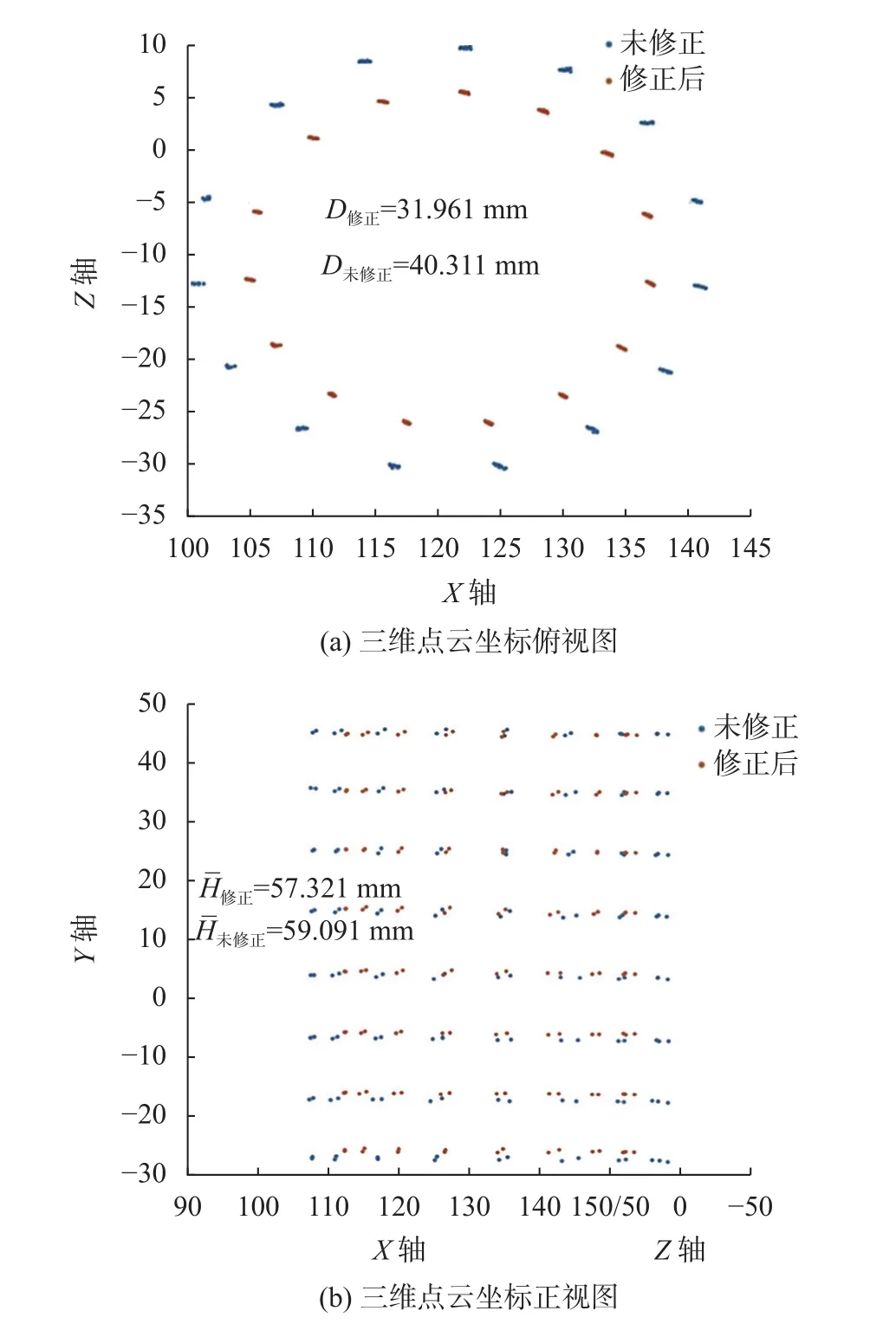
图6 三轴模型修正前后形态对比

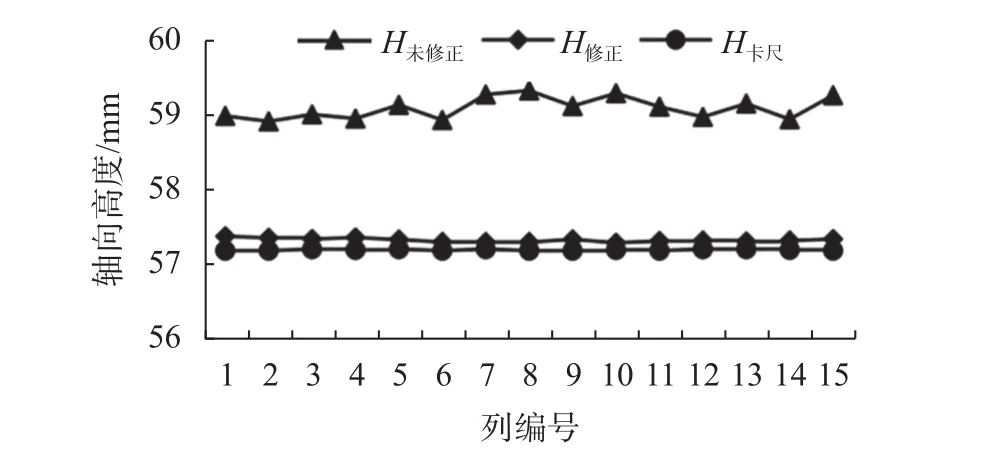
图7 三轴模型轴向高度修正前后与卡尺测量值对比

从图6可见，由于多重介质的折射影响，充水后的压力室内三轴模型径向与轴向均呈现出折射放大现象。但折射对三轴模型轴向与径向的影响不一致，相对于轴向，径向受折射影响的作用更为显著，与图2实际观察的结果相吻合。分析其原因，在径向上压力室玻璃罩为一弧形曲面，使得充水后的压力室如同一面透镜，因此三轴模型的径向测量不仅受多重介质的折射影响，还受到压力室弧形曲面影响，导致成像光线在弧形曲面处发生明显的曲折[22]，成像时三轴模型的径向直径呈现明显的放大变形现象，径向测量平均值从 31.961 mm（D修正）放大至40.311 mm（D未修正），差值为 8.35 mm，其平均误差增加26.29%；在轴向上压力室玻璃罩如同一面平面玻璃，由于平面状玻璃受到折射的影响较小[8]，并且水、有机玻璃压力室及空气三者的折射率相近[15]，成像光线受不同介质的折射的曲折程度较小，使得三轴模型轴向测量时呈现的折射放大现象相对不明显，轴向测量平均值从57.321 mm（）放大至59.091 mm（），差值仅为 1.77 mm，其平均误差增加3.09%。同时，根据图7模型轴向高度修正前后与卡尺测量值对比的结果分析，从图上可见，尽管轴向受折射的影响作用相对要小，但其测量值与三轴模型实际测量值仍存在明显差异。在进行折射修正前H未修正值均大于H卡尺值，此时每列轴向高度测量值波动幅度较大，从58.9 mm附近变化至59.3 mm上下波动，而折射修正后H修正测量值曲线变化幅度较小，与H卡尺测量值曲线近似平行，二者差值明显减小。

由此表明，折射修正模型可以较为准确地修正折射所产生的放大变形，获取趋近三轴模型原状的三维模型。此外，成像时三轴模型轴向高度受折射影响并非呈一定比例放大，而是在某一范围内波动，产生上述现象的原因主要是试验受到相机拍摄的方位与角度、光照环境稳定程度以及玻璃材质的均匀程度等影响，三轴模型各方向受到的折射影响不一致，折射对三轴模型成像的影响存在波动。结合表3、表4数据分析，以空气中卡尺测量的平均值作为“基准值”，折射修正后的轴向测量平均误差为0.23%，径向测量平均误差为0.63%，这与折射修正前的轴向测量平均误差减少3.09%，径向测量平均误差减少26.29%。上述试验结果表明，通过基于光线追踪的折射修正模型可以将折射所致误差控制在试验允许的范围，将考虑折射因素的摄影测量法用于土工三轴试验，基本满足三轴土样变形测量的精度要求。

4 结束语

本文通过空气中的精度验证试验初步评估摄影测量法在空气中拍摄测量的准确性。以硬质圆柱体作为三轴土样模型，通过摄影测量的三轴模拟试验对三轴试验中摄影测量的精度进行验证，分析压力室与水引起的折射对三轴模型的成像影响以及折射修正模型处理折射问题的效果。同时探讨将考虑折射影响的摄影测量法用于三轴试验的适用性，得出以下结论：

1)在空气中进行精度验证试验，摄影测量结果与游标卡尺测量结果基本吻合，点间距测量值绝对误差在0.025 mm以内，摄影测量法在空气中具有较高的测量精度。

2)不同介质的折射对三轴模型的成像有重要影响，基于光线追踪的折射修正模型可以有效减少折射引起的测量误差，经修正后的径向平均误差为0.63%，轴向平均误差为0.23%，这与折射修正前的径向测量平均误差减少26.29%，而轴向测量平均误差减少3.09%。

3)在折射修正前后，摄影测量径向直径平均值从31.961 mm放大至40.311 mm，而摄影测量轴向高度平均值从57.321 mm放大至59.091 mm，从数值变化可知，径向受折射的影响显著大于轴向。此外，三轴模型各方向受到的折射影响各不相同，成像时三轴模型各向轴向高度在某一范围内波动，并非按照一定比例放大变形。

目前摄影测量法应用研究尚且不足，测量系统中还存在一系列误差，如成像系统误差、折射修正参数误差、外部环境误差等，有待进一步完善。从以下方面提出减少相应误差的建议与措施：1）升级相机成像采集系统。引起相机成像系统误差的主要因素为相机参数与图像分辨率。今后可配备具有高精度参数的相机与高图像分辨率的相机成像采集系统，从而提高摄影测量的精度以及图像处理的效率。2）完善折射修正模型。折射修正模型参数是影响摄影测量法在三轴试验测量精度的主要因素之一，该误差是模型参数与实际值存在偏差引起的。故而今后对折射修正模型进行完善，以获取准确性更高的模型参数组合，从而构建更精确的折射修正模型。3）研发自动化补光模块。拍摄过程中光照强度过强或过弱会导致拍摄的图像曝光过度或曝光不足，影响图像的成像质量。因此，有必要研发配备自动化补光模块减小外部环境所致误差。