大尺寸矩形工装在实际振动试验中的应用

孙杰明,杨静静

(中航富士达科技股份有限公司泰斯特实验室,西安 710077)

0 引言

在振动试验中，工装作为一个机械结构件，其结构、尺寸、重量都会对最终的试验结果产生较大的影响，通常来讲，振动台的台面尺寸是一个固定值，由于不同振动条件的限制，即使是增加扩展台，台面的大小也不可能满足所有工装的需求，所以有必要研究当振动工装的尺寸超出振动台面时，是否可以进行试验，以及确定能够进行试验的最大伸出部分。

1 挠度模型

由于在进行振动试验过程中，振动工装的尺寸超出振动台面的尺寸时，在实际的工程测量中，对于超出部分并没有明确的标准规定[1-2]，其是否可以进行试验。以正弦振动为例，在操作振动台时，会给出振动试验所需要的条件参数，以及相应的容差范围，同时未超出部分通常以螺接的形式安装。可以将这种安装方式，简化为一个近似的悬臂梁模型，如图1所示：

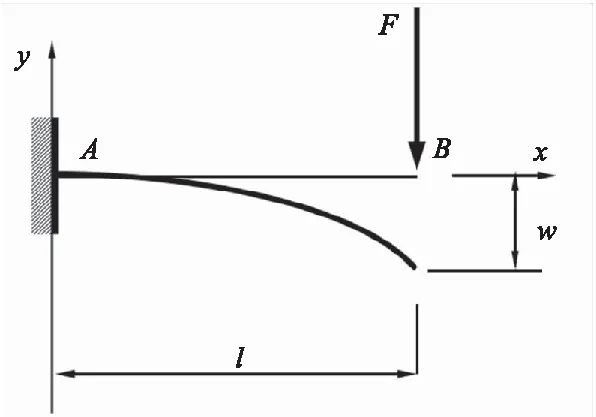
图1 悬臂梁模型图Fig.1 Cantilever beam model drawing

为了方便研究可忽略矩形工装的厚度，A点及A点之后为矩形工装的未伸出部分，并且采用螺接固定的方式，其中x为弯距，L为矩形工装的伸出长度，由于A点处与台面螺接，可以将A点和振动台台面看做一个整体，A点会受到振动台的激振力，因为AB为一个整体，所以在B端也会有一个力F,在这里假设力的方向向下，其中w也就是在材料力学中经常提到的挠度，在忽略剪力对矩形工装位移的影响时，曲率与弯曲半径的关系为：

(1)

其中M与ρ都是关于x的函数：

(2)

其中ρ为曲率，M为其弯距，对式(1)和式(2)变形可得：

(3)

由于w′2与1相比非常小，所以式(3)可化简为：

(4)

同时规定在图1中x，y箭头所指的方向为正，曲线向上凹陷时w为正，同时M为正，曲线向下凹陷时w为负，同时M为负，则说明w与M同号则式(4)可变为：

(5)

这也是在工程上使用的梁的近似挠曲线微分方程，其中M为关于x的函数，EI为矩形工装的刚度，w为挠度，由于在进行振动试验时，工装的尺寸和结构都已经固定，因此，此处的材料刚度EI为常量，所以式(5)可改写为：

EIw″=M(x)

(6)

对w求二次积分可得

(7)

其弯距方程：

M(x)=-F(L-x)

(8)

则式(5)、式(6)可以改写为以下形式：

EIw″=-FL+Fx

(9)

同时对该表达式进行积分可得：

一次积分：

(10)

二次积分：

(11)

由于A点处螺接于振动台，可以将螺接部分与振动抽象为一个质点，因此A点处x=0，w=0，w′=0，带入式(10)和式(11)中可知C1和C2都为0，因此矩形工装的最终挠度公式为：

(12)

由于矩形工装的挠度为挠曲线的方向求其二次积分而来，在实际工程测量中以GJB360B—2009《电子及电器元件试验方法》中方法204的高频振动条件为例[3-4]，挠度的最大值wmax为位移幅值的±15%时，弯矩x有最大值。在实际振动试验时，由于振动时的位移和加速度可从振动曲线中直接得出，带入式(12)中，即可求得最大伸出量，根据实际测试，矩形工装的伸出量应不大于扩展台面的50%。

2 应力疲劳

在试验幅值满足相应容差的要求时，矩形工装板伸出部分的疲劳强度，也是必须考虑的问题，在实际试验过程中，因为工装或者产品因疲劳而产生的裂纹和断裂现象时有发生，而疲劳的本质是：在交变应力作用下，材料的结构受到多次重复变化的载荷作用后，应力值虽然始终没有超过材料的强度极限，甚至比弹性极限还低，在交变载荷的重复作用下而产生的材料和结构的破坏[5-6]。这种现象的产生，并非因为试验中某一项试验参数的设置错误，或者是实际幅值与规定幅值不符时，造成的试验失败。因此判断这种现象发生的概率也是整个实验过程中必须要解决的问题。还是以悬臂梁为模型，其最大应力为：

(13)

同时规定正向力为：

(14)

其中D为位移量，E为弹性系数，W为弹臂宽度，T为弹臂厚度，l为力臂长度,σ为最大应力，F为理论正向力，以正弦振动为例，在进行试验时，由于正弦振动的周期性，材料或者结构发生破坏的疲劳载荷也是大小和方向随时间周期性变化的交变载荷，应与其大小相等，方向相反，因此这种交变在载荷又被称为循环交变力，如图2所示：

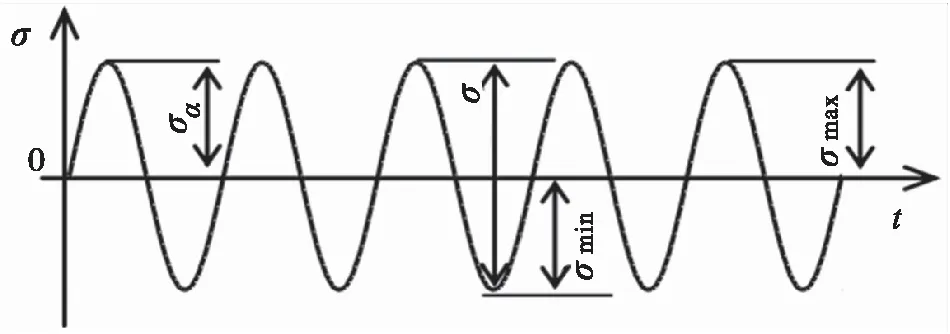
图2 对称循环交变载荷Fig.2 Symmetrical cyclic alternating load

其实伸出部分不仅会受到动载荷的作用，而且也会受到静载分量的影响[7-8]，这样在动静载荷的同时作用下，图2中应力随时间的变化的曲线就变成图3的形式：

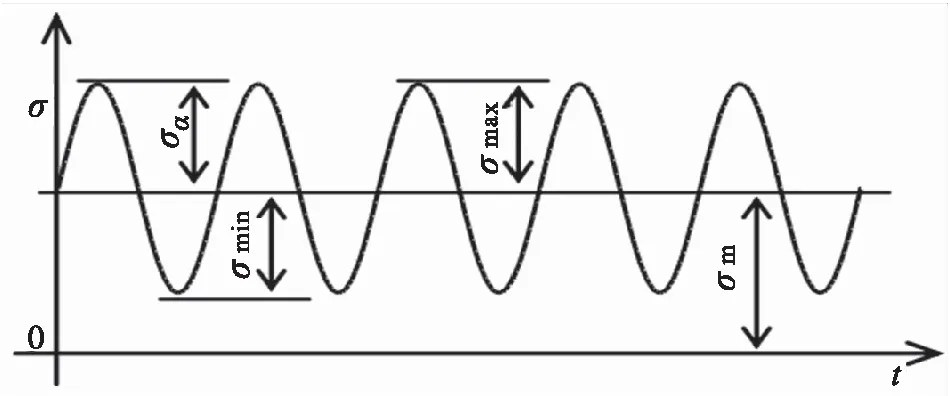
图3 不对称循环交变载荷Fig.3 Asymmetric cyclic alternating load

从数学角度来看，图3的变化就在于，图3是将图2整体向正方向平移了一个静载荷分量，而此时的应力比从R=-1变成了R≠-1，一般情况下，材料所承受的循环载荷σ的应力幅越小[9-10]，到发生疲劳断裂时的应力循环次数就越大，就材料来说，振动工装一般选择的材料多为铝合金材料，由铝合金材料的S-N曲线(图4)可知：

图4 铝合金应力-应变曲线Fig.4 Stress-strain curve of aluminum alloy

其横标为应力循环次数，对应的纵坐标为应力幅，其叙述关系式可以用σmN=C来表示，其中σ为应力幅或者最大应力，N为达到应力疲劳极限时的次数，m，C为材料常数，在第一节中，通过矩形工装板的悬臂梁简化模型得到了在该种状态下板子所受到的最大应力值，N则可以表示为，设定振动条件下的时间振动次数，所以可以通过计算一次扫频振动次数来计算总循环数下的振动次数，将一次扫频循环的振动次数记做N1，同时

(15)

其中f2和f1分别为终止和开始频率，而Re为以e为底的对数扫频速率，通常这个速率在正弦振动试验中都是以倍频程的形式给出，因此式(15)中的Re需要更换为以倍频程表示的扫描速率，根据换底公式:

⟹Re/R2=(ln 2)=0.6392

(16)

将式(16)带入式(15)可得：

(17)

其中n为倍频程数，T为从f1扫到f2的扫描时间，当总的扫频数为M时，得到总的振动循环次数为：N=2N1M。由前文可知在铝合金材料的S-N曲线中，当N或σ已知时，可以根据式(17)计算或者由S-N曲线量出，矩形工装板应力疲劳时的应力循环数，或者应力幅。因此在判断该矩形工装板在试验周期内是否发生断裂，只需满足以下要求：

①当应力幅已知，应力循环次数<应力疲劳极限时的应力循环次数；

②当应力循环次数已知，实际应力值<应力疲劳极限的最大应力。

3 常用夹具型式分析

实际振动试验中，夹具的型式种类复杂，彼此差别很大，很难一一分析和介绍，在此分析两种最为常见的转接平板型夹具和锥体形夹具，这两种振动工装在超出台面时的振动情况。转接平板型夹具如图5所示。

图5 带通孔型及带T型过渡板Fig.5 With through-hole and T-shaped transition plate

因为产品的安装螺孔和振动台面的螺孔对不上，必须在产品和台面之间加一块过渡平板，称为平板型夹具。平板的厚度通常为20～30mm，沉头螺栓的过孔与台面上的螺孔位置一致，过孔的深度不低于10mm，沉头螺栓埋头孔的深度大约是螺杆直径的1.5～2.0倍[11]。安装试件用的螺孔与产品的安装孔的位置一致，平板的材料视产品的重量及结构状况而定，多为钢材、铝板或铝镁合金，通常平板呈圆形，最大直径已不超出振动台外缘为最佳，通过式(12)的计算，当超出振动台的外伸长量长度等于板厚时，对于该平板的谐振频率值影响较小[12-13]，若超出振动台面的外伸量达到4倍的板厚时，则此平板的谐振频率可能下降到原有谐振频率值得1/2～1/3，则此时当应力幅已知时，极限应力循环次数为之前的1/2～1/3，极限应力值同时也降低为之前的1/2～1/3，则通过式(17)的结论可知：

①当应力幅已知，应力循环次数<应力疲劳极限时的应力循环次数；

②当应力循环次数已知，实际应力值<应力疲劳极限的最大应力。

通过上述结论可知，转接平板型夹具如果超出振动台面的外伸量达到4倍的板厚时，式(8)的结论由小于关系改为趋近关系。这对于振动试验显然是不利的。

锥体形夹具如图6及图7所示，当产品底部尺寸超出振动台面范围，可以制作倒锥体形过渡头(夹具)，对于一些上限频率较高的振动试验，倒锥体形过渡头(夹具)上下两个台面半径之差(ΔR=RS-RX)与过渡头高度(H)之比不能过大，经过粗略计算当ΔR/H小于1:1.7时[14]，且锥体的张开角度为60°时满足：

①当应力幅已知，应力循环次数<应力疲劳极限时的应力循环次数；

②当应力循环次数已知，实际应力值<应力疲劳极限的最大应力。

图6 正锥体形夹具Fig.6 Regular cone clamp

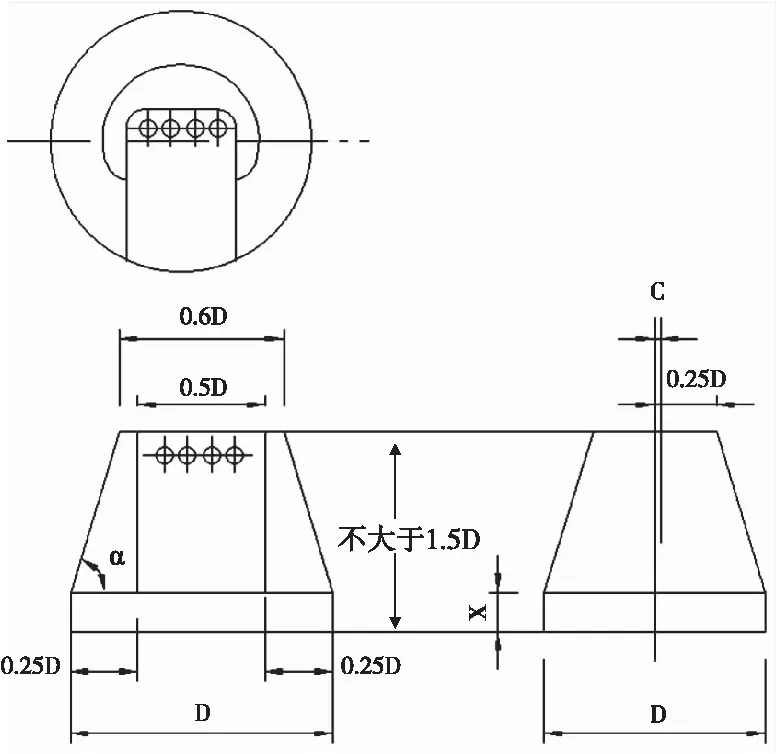
图7 倒锥体形夹具Fig.7 Inverted cone clamp

满足某些特殊试件的需要，也有一种正锥体形的夹具如图7所示，图中的尺寸是一个特例。通常锥体底端的仰角α为60°，真椎体形夹具的最大高度不应超过锥体底部直径的1.5倍，夹具的最低高度以锥体底端仰角α不小于30°为限。

4 结论

在所进行的振动试验中，一般情况下会附带有相应的工装，而工装的设计者受制于自身对试验的认知不足或者对试验所使用的设备参数了解不多的情况下，只按工装设计的通用理论来设计工装，造成工装的尺寸超出振动台面的情况时有发生，在此情况下，加大扩展台，或者重新设计振动工装都是非常低效的，因此应用式(17)与式(12)的结论，则可以判断振动工装在振动过程中是否可以应用。