基于磁势矢模型的电磁直线驱动装置解析建模

江金昊，葛文庆，李 波，王 赓

(山东理工大学交通与车辆工程学院，山东淄博 255000)

电磁直线驱动装置具有结构简单、可靠性高、功率密度大[1]、响应速度快[2]等优点，在航空航天、船舶及车辆等直线运动领域具有较为明显的应用优势[3-4]。近年来，越来越多的国内外学者对其进行了更为深入的探索，理论及工程研究逐渐系统化，但仍有一些较为基础的研究有待完善。

对电磁直线驱动装置的研究大多围绕有限元进行[5-7]。有限元法在解决复杂电机结构的磁场分布时具有求解精度高且通用性能较好等优点，但有限元法求解时运算周期较长[8]，同时无法直观反映磁场特性与尺寸参数之间的规律，且采用有限元法对电机进行参数化设计时效率较低，因此现阶段有限元法大都用来对模型的正确性进行验证[9-11]。近年来，部分学者开始围绕解析法对电磁直线驱动装置进行研究，现阶段常见的解析方法有磁势矢模型、等效磁网络模型及保角变换模型。文献[12]、文献[13]及文献[14]建立磁势矢模型对动磁式驱动装置的电磁特性进行研究，该方法虽较为直观地反映尺寸参数对电磁特性的影响，但边界条件复杂且计算量庞大；文献[15]采用保角变换法分析直线电机特性，得到电机内部磁场分布规律，虽然准确度较高，但该方法需要多次变换平面，增加了求解难度；文献[16]、文献[17]及文献[18]建立等效磁网络模型分析旋转电机内部磁场分布，该方法的本质为集总参数法，具有一定的局限性，无法得到电机内磁场分布规律。

为了获悉电磁直线驱动装置稳态电磁特性与各尺寸参数间的关系，采用磁势矢模型进行求解，采用分离变量法准确计算开路状态下驱动装置静态磁场分布以及电磁力。首先，建立动圈式电磁直线驱动装置解析模型，得到驱动装置电磁特性与各尺寸参数间的关系；其次，设计样机并通过有限元模型对解析模型加以验证；最后搭建试验平台，并通过试验验证解析模型的正确性与精确性。

1 结构与模型

电磁直线驱动装置用于课题组自主研发[19]的直驱式自动变速器[20](direct drive AMT，DAMT)，具体结构如图1所示。该变速系统由2个拨叉控制4个挡位，选用1对电磁直线驱动装置分别驱动拨叉进行单自由度往复运动，进而实现换挡。由于引入了驱动装置，该变速系统缩短了动力传动路径，提高了传动效率，具有结构紧凑、控制简单且换挡时间短等优点，其中电磁直线驱动装置作为驱动单元，其特性直接决定换挡品质，因此对该驱动装置电磁特性的研究是十分有必要的。

电磁直线驱动装置结构如图2所示。驱动装置由内外磁轭、端盖、线圈、线圈骨架及永磁体等部件组成。其中内外磁轭及端盖由导磁性能较好的S10C制成，永磁体为高性能N42SH永磁材料烧结而成，线圈骨架由硬度较高的PTEF制成。为了提高驱动装置单侧磁通密度且实现磁场的自屏蔽，引入Halbach永磁阵列。

图1 DAMT样机Fig.1 Prototype of DAMT

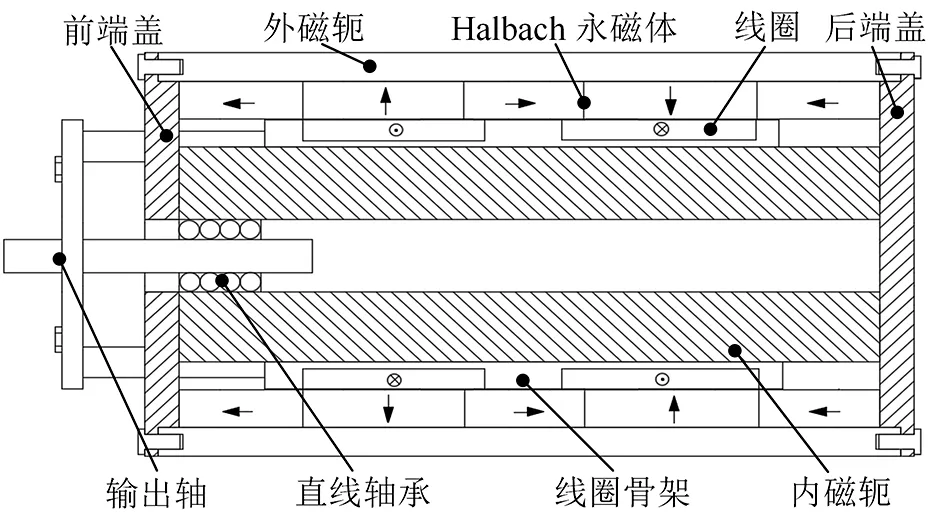
图2 电磁直线驱动装置结构Fig.2 Structure of electromagnetic linear drive device

2 电磁场及电磁力建模

2.1 开路磁通密度建模

电磁直线驱动装置实际边界条件较为复杂，为降低求解难度应在精度允许范围内做出如下假设：

1)驱动装置内部各接触面均光滑且紧密贴合；

2)为便于傅里叶级数展开，认为模型沿轴向尺寸可无限延伸；

3)该驱动装置为无槽结构且内磁轭较厚，可以忽略端部效应及饱和效应；

4)永磁体内部相对磁导率为常量μr，内、外磁轭相对磁导率为无穷大。

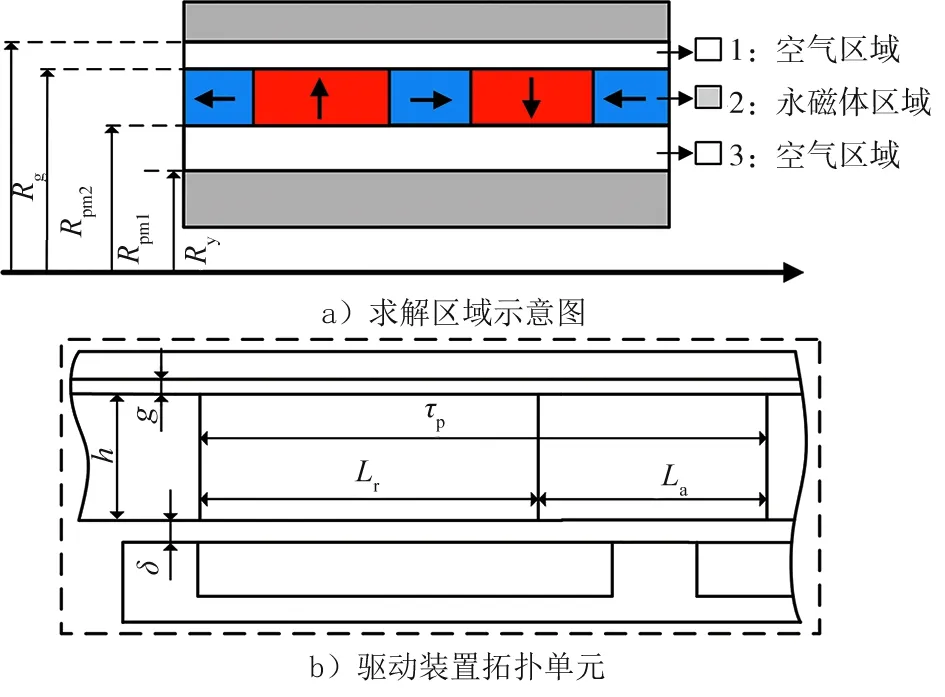
图3 驱动装置简化模型 Fig.3 Simplified model of drive device

因此可以建立如图3所示的驱动装置简化模型。其中图3 a)为求解区域示意图，为了定义边界条件完成求解，建立了图中的空气区域1，该区域在实际中不存在；图3 b)为驱动装置拓扑单元。

通过磁势矢模型求解驱动装置内部磁场分布时，需要先建立求解区域内磁场强度与磁通密度的本构关系，并引入二维坐标磁势矢作为辅助求解手段，以此对求解区域内的麦克斯韦方程进行求解。各求解区域中存在如下本构关系：

(1)

式中：B为磁通密度；H磁场强度；M为磁化矢量；χm为磁化率；M0为剩余磁化强度；μ0为真空磁导率。

在求解磁场分布之前，需要得到磁场控制方程，求解电磁直线电磁驱动装置内部磁场分布的本质是寻找在特定边界条件下的麦克斯韦方程组的特解。磁场为无源场，在各区域内均满足磁通连续性原理以及麦克斯韦全电流定律：

(2)

式中：D为电位移矢量；J为电流密度。

引入磁势矢B=∇×A，可得到各求解区域内磁场控制方程：

(3)

电磁直线驱动装置中电磁场的变化为低频，因此在计算时可认为是准静态场，可以忽略位移电流的影响，即D≡0。同时在区域1,2,3中均无电流，即Ji=0。因此可以得出简化后磁场控制方程：

(4)

由于电磁驱动装置为管状直线电机，其内部磁场具有周向对称性，因此可以将磁场控制方程在二维坐标系下进行简化，将磁势矢A在柱坐标系下分解后，可以进一步将各求解区域内磁场控制方程简化：

(5)

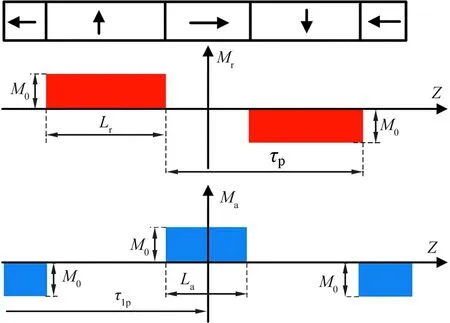
图4 磁场强度空间分布 Fig.4 Spatial distribution of magnetic field intensity

驱动装置永磁体选用Halbach阵列分布，该磁极分布由轴向充磁与径向充磁的永磁体根据一定规律组合而成，该分布相较于单一径向分布，可以在提高一侧磁通密度的同时实现磁场自屏蔽。在求解时需先将磁化矢量在柱坐标系下进行分解，永磁体磁化矢量的空间分布如图4所示。

图4中M0为磁化矢量的绝对值，其计算如下：

(6)

式中Bre是永磁体的磁体剩磁。

将图4中不同方向的磁化矢量展开成傅里叶级数可得：

(7)

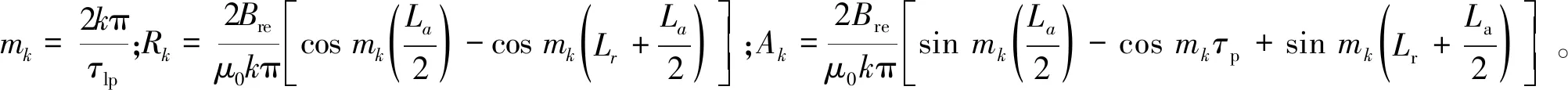
其中：τlp为模型周期；τp为极距；Lr为径向充磁永磁体长度；La为轴向充磁永磁体长度。

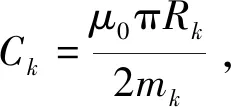
(8)

联立公式(本构关系、磁势矢通解、磁势矢定义)，可以得到不同求解区域下径向及轴向的磁通密度以及磁场强度的分布，具体结果如式(9)及式(10)所示。

在区域1及区域3中：

(9)

在区域2中：

(10)

式中：a1k，a2k，a3k，b1k，b2k，b3k为待定系数，可根据边界可通过具体边界条件求得；In(x)，Kn(x)，Ln(x)分别为n阶第1类贝塞尔函数、第2类贝塞尔函数及斯特鲁夫函数，其函数均不可由初等函数表示，但可以在自变量等于0处用泰勒公式以及Gamma函数进行如下逼近：

(11)

在进行模型简化时认为电磁驱动装置各平面均为光滑且紧密贴合，介质分布均匀。考虑到边界条件为磁通密度在介质交界处法向连续、磁场强度在该处切向连续，因此可以得到对应边界条件：

(12)

进而得到在此边界条件下的各待定系数，将各系数代入式(9)及式(10)，最终可确定唯一的磁通密度表达式。

2.2 电磁力推导

电磁驱动装置的运动满足洛仑兹定律：

(13)

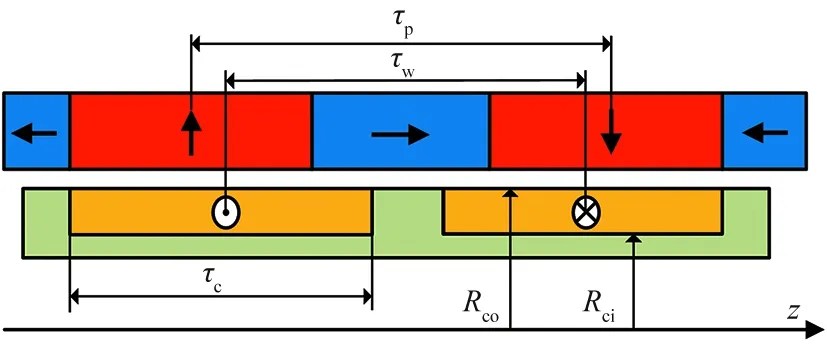
图5 线圈尺寸示意图Fig.5 Schematic diagram of coils

电磁驱动装置内结构及磁场均具有周向对称性，线圈及永磁体部分尺寸参数如图5所示。线圈部分可近似看作矩形，其积分区域可分别表示为

(14)

式中：Rci为线圈区域内径；Rco为线圈区域外径；τc为线圈区域轴向长度；τw为线圈节距。

为便于求解电磁力，可以进一步将式(13)在二维平面内进行简化，得到线圈1的洛伦兹力为

(15)

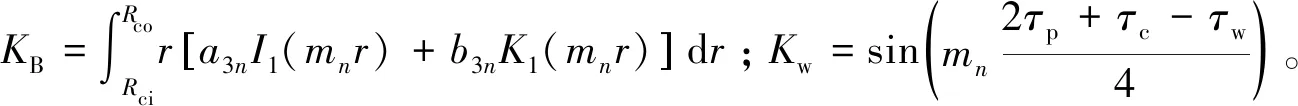
同理可以得到线圈2的洛伦兹力，并最终得到电磁驱动装置的电磁力为

(16)

3 有限元验证及结果讨论

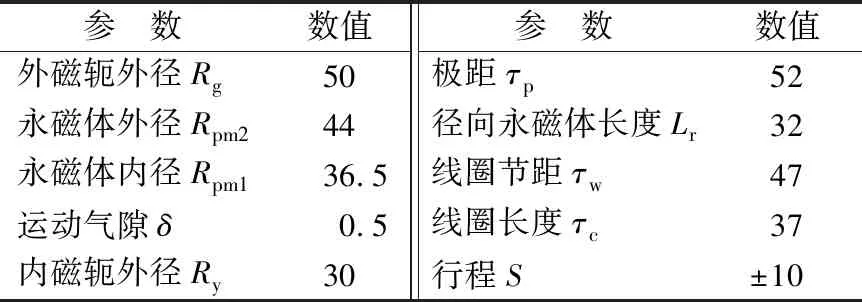
表1 电磁直线驱动装置尺寸参数Tab.1 Dimension parameters of electromagnetic linear drive device 单位：mm

为了验证解析模型的正确性，需要将解析结果与求解精度较高的有限元结果进行对比分析，对电磁直线驱动装置进行分析，仿真以文章所描述的电磁直线驱动装置为对象，该驱动装置为课题组自主设计研发，并已对其尺寸进行优化[21]，优化后参数如表1所示。

在JMAG Designer电磁场仿真软件中建立有限元模型，采用有限元对电磁直线驱动装置进行静态磁场仿真，可以得到径向磁通密度与驱动装置轴向尺寸的关系，结果如图6所示。由图6可知，解析结果与有限元结果吻合较好，证明了解析的正确性；永磁体具有边缘效应，其磁化矢量在边界的分布并不均匀，而磁势矢模型在简化时认为永磁体区域的磁化矢量为均匀分布且其数值为M0，因此有限元得到的高磁通密度区域会略小于解析模型得到的结果；磁势矢模型中内外磁轭磁导率均为无穷大，忽略了内外磁轭的磁阻，从而使得解析模型的磁通密度均值以及波动率均略大于有限元模型。

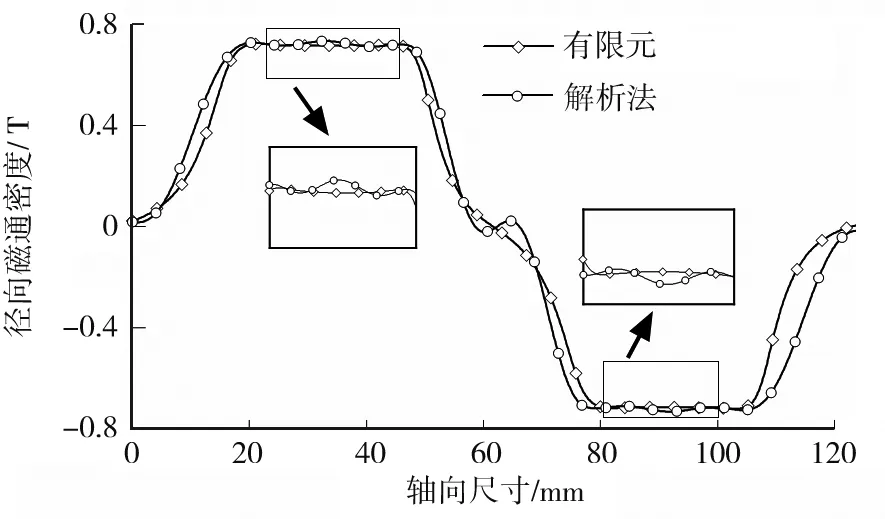
图6 径向磁通密度对比图Fig.6 Contrast diagram of radial flux density

图7为电磁力、相对误差与行程之间的关系，图中将有限元结果与解析结果进行比较，驱动装置工作电流为I=10 A，最大行程为10 mm。为了更加直观地反映解析模型的求解精度，引入相对误差，定义为

(17)

式中：FAna和FFem分别为解析和有限元得到的电磁力结果。

为了反映电磁力的波动情况，引入电磁力波动率，定义为

(18)

式中：FMax和FMin分别为电磁力的最大值和最小值。

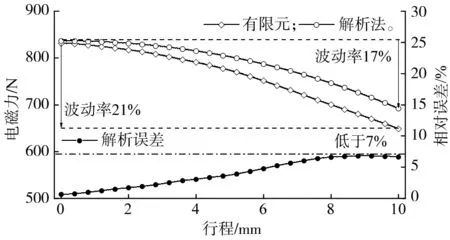
图7 电磁力及误差对比图 Fig.7 Contrast diagram of electromagnetic force and error

从图7可知，电磁力随着行程的变化规律为非线性的，且随着行程的增大，电磁力逐渐降低，有限元结果与解析结果吻合较好，证明了解析模型的正确性。解析模型初始位置处电磁力为836 N，最大行程处电磁力为694 N，力波动率为17%；有限元模型初始位置处电磁力为831 N，最大行程处电磁力为651 N，力波动率为21%。存在误差的原因可能如下：解析模型的径向磁通密度大于解析模型，使得积分项的B3r项较大；在求解时将线圈区域简化为矩形，但实际导线间存在空隙，因此线圈积分区域略大于实际区域。相对误差最小值0.6%，随着径向磁通密度误差随行程的叠加，相对误差逐渐增大，最大值为6.6%。

有限元求解过程中，建立三维模型进行有限元仿真，求解周期约为120 min；建立二维模型进行有限元仿真，求解周期约为25 min；解析模型的求解周期可控制在10 s以内。解析模型的求解周期远小于有限元模型，因此在误差允许的范围内，选用解析模型获悉电磁直线驱动装置稳态电磁特性时间成本较低。

4 测试平台搭建与试验验证

4.1 试验平台搭建

图8 试验平台Fig.8 Testing platform

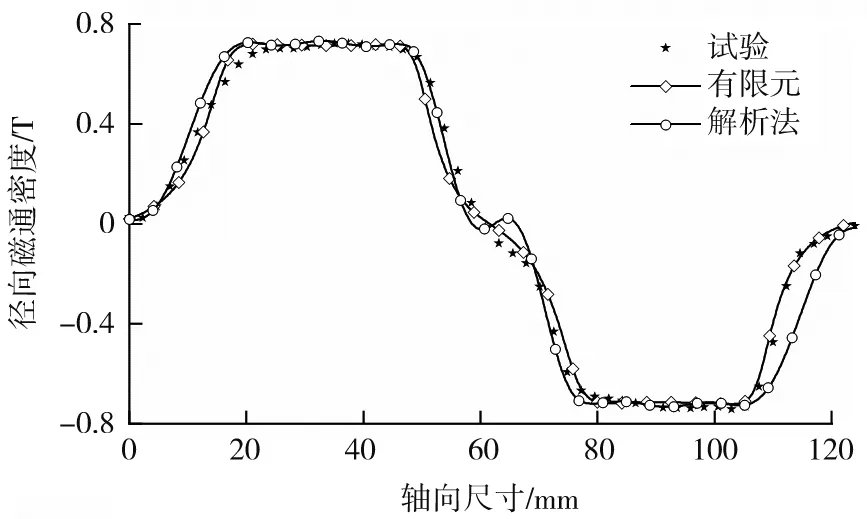
图9 磁通密度试验结果及对比Fig.9 Contrast diagram of magnetic flux density test results

试验平台如图8所示，其中图8 a)为磁场测试平台，该平台包括电磁直线驱动装置、保持架、上位机、IL-300CMOS激光位移传感器及三维高斯计及霍尔探针，霍尔探针可以插入驱动装置内部，用于测量电磁直线驱动装置内部气隙处的磁场分布。

图8 b)为电磁力测试平台，该平台主要部分为电磁直线驱动装置、支撑平台、IL-300CMOS激光位移传感器(量程±120 mm，灵敏度0.2 mm)、S9M力传感器(量程2 kN，灵敏度0.4 N)、RUT-BOX控制单元、驱动单元、直流电源(最大输出60 V)、上位机等，该平台用来测量电磁力与行程的关系。

4.2 试验结果与分析

在测量驱动装置径向磁通密度时无电流负载，轴向采样间隔为2 mm，试验与有限元以及解析的对比图如图9所示。由图9可得：在轴向尺寸范围内，试验结果与解析模型和有限元结果吻合较好，永磁体中间位置处的误差为加工尺寸误差造成的测量误差，永磁体边缘处的误差源于永磁体安装过程的轴向间隙，误差均在接受范围内，证明了解析模型的正确性。

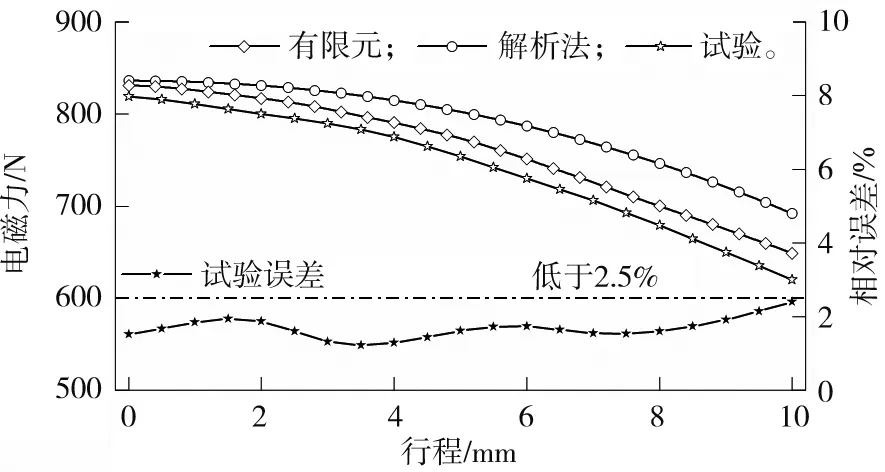
图10 电磁力试验结果及对比Fig.10 Contrast diagram of electromagnetic force test results

该驱动装置用于DAMT系统，因此在试验时需模拟DAMT换挡过程，结合课题组对DAMT换挡力的研究[3]，选择绕组通入电流为10 A。为简化实验过程，仅对单侧行程进行试验，沿轴向采样间隔为0.5 mm。选用力传感器测量电磁直线驱动装置的电磁力，用位移传感器测量行程。试验与有限元以及解析模型的对比如图10所示。由图10可知：在驱动装置行程范围内，试验结果与解析模型和有限元结果吻合较好，证明了解析模型的正确性。试验结果低于有限元结果，原因可能如下：一是永磁体在生产安装时均存在误差，进而产生气隙，弱化磁场分布；二是线圈绕组存在间隙，实际绕组匝数小于仿真设置匝数。试验得到电磁力最大为820 N，出现在行程0 mm的位置；误差最大为2.48%，出现在行程10 mm处。

5 结 语

本文针对直驱式自动变速器用动圈式电磁直线驱动的装置解析建模与电磁特性分析，主要结论如下：推导了磁势矢模型下的动圈式电磁直线驱动装置内磁场分布及电磁力的表达式，并通过有限元及试验对解析模型进行验证，得到解析模型与有限元模型最大误差为6.6%，与试验的误差不超过2.5%，证明了解析模型的正确性及精确性。

本文所选用的磁势矢模型只能满足较低精度下的电磁直线驱动装置建模，未来还需完善更多混合模型下的驱动装置解析建模，以提升建模精度。