巧构直线方程 让函数不等式放缩有“度”

浙江省安吉县高级中学

林兰兰

函数不等式的放缩问题不仅是学生学习的难点，更是近年来各地高考命题的一个热点.其思维的独特性、解题手段的灵活性、知识内容的综合性等特点，在对形成学生理性思维、科学精神和促进学生个人智力发展的过程中发挥着重要作用，但也使不少学生望而却步.笔者选取构造直线方程的角度谈谈如何把握函数不等式放缩的“度”.

1 构造垂线放缩

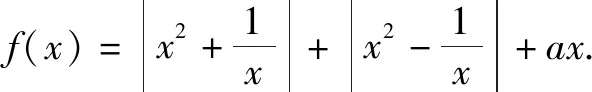
(1)当a=0时，判断函数f(x)的奇偶性；

(2)若f(x)≥4x-6恒成立，求a的取值范围；

(3)设b∈R，若关于x的方程f(x)=b-8有实数解，求a2+b2的最小值.

解析：(1)(2)略.

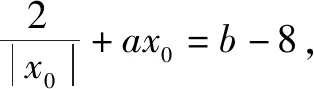
点评：本题从a2+b2的结构出发，联想到原点与点(a,b)的距离的平方.点(a,b)的轨迹是什么？从已知条件出发，构造两条直线方程，巧妙地利用“垂线段最短”，使问题获解.

2 构造切线放缩

例2(2020年高考全国卷Ⅰ第21题)已知函数f(x)=ex+ax2-x.

(1)当a=1时，讨论f(x)的单调性；

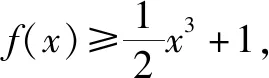
解析：(1)略.

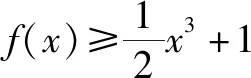
①当x=0时，得a∈R.

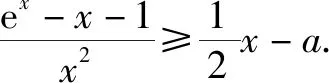
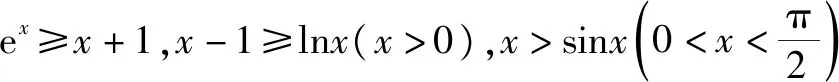
3 构造割线放缩

例3(2021年高考全国卷Ⅰ第22题)已知函数f(x)=x(1-lnx).

(1)讨论f(x)的单调性；

解析：(1)略.

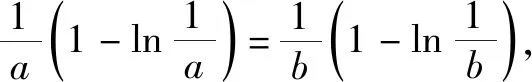
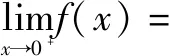
对x1进行割线放缩：作直线y=x，其与直线y=m交于点(m,m)，而y=m与y=f(x)交于点(x1,m)，于是x1

对x2进行切线放缩：作y=f(x)在(e,0)处的切线：y=-x+e，它与直线y=m交于点(e-m,m)，故x2

从而x1+x2

点评：本题以直代曲，抓住函数在特定范围内区间端点特征，对x1进行割线放缩，对x2进行切线放缩，合理把握了放缩的“度”.这种放缩方法，需要充分理解函数的图象性质，特别是函数的单调性和凹凸性.它不同于常见的放缩手段，让学生有耳目一新之感，这对学生数学思维的拓展大有帮助.

4 构造隐性直线放缩

(1)求f(x)在x∈(0,1]上的最大值；

(2)若g(x)≤0对任意的b∈[a,+∞)及x∈(0,1]恒成立，求实数a的取值范围.注：e是自然对数的底数.

解析：(1)易得f(x)的最大值为f(1)=2.

(2)由于g(x)≤0对任意x∈(0,1]恒成立，故g(1)≤0.而g(1)=-2ab-2a+2b+2=-2(a-1)·(b+1)，且b≥a>0,所以a≥1.

下面证明当a≥1时，恒有g(x)≤0.

g(x)≤-2abex-1+b(2x-2)-2a+2b+2

=-2abex-1+2bx+2(1-a) ≤

-2abex-1+2bx

=2b(x-aex-1)≤

2b(x-ex-1).

因为ex≥x+1(切线放缩)，所以ex-1≥x，因此g(x)≤2b(x-ex-1)≤0.

综上可得a≥1.

点评：含多个参数的不等式恒成立问题，往往先是必要性探路，再论证其充分性.本题对(x+1)lnx的放缩，采用了待定系数法，借助第(1)问的结论，构造出直线y=2x-2，使问题在不断的放缩中逐渐柳暗花明.