混合模型算法在无波前传感自适应光学中的应用
刘武杰,元秀华,周泽宇,李 奇,赵 茗
华中科技大学光学与电子信息学院,湖北 武汉 430074
1 引 言
空间光通信具有容量大、数据传输速率高、抗电磁干扰能力强、安全保密性好等一系列优点,是构建空天地通信网络的不可或缺的信息传输方式之一。然而,在星-地自由空间光通信中,湍流大气效应给光学系统引入畸变像差,不仅会造成传输光束扩展、漂移及闪烁[1-5],还会导致通信系统耦合效率下降、信噪比降低、误码率增加。因此,校正光场相位随机变化引起的波前畸变像差,是自由空间光通信面临的关键技术问题[6-10]。
在空间光通信系统中,引入无波前传感自适应光学技术,是校正湍流大气产生的畸变波前的有效方案。近些年对无波前传感自适应光学系统的研究中,各种寻优算法相继被提出:2015 年,牛超君[11]分别采用差异进化(DE)算法、模拟退火(SA)算法和SPGD 算法对不同湍流强度下波前畸变的校正过程进行了仿真,当大气相干长度r0=0.04 m~ 0.1 m 时,处于NRZOOK 调制下的FSO 系统的误码率均能够降低到10−6以下满足通信要求;2018 年,顾海军[12]将粒子群优化(PSO)算法应用到无限电力传输系统中,通过自适应光学(adaptive optics,AO)技术使光伏面板的光电转换效率从40.58%提升到79%,大幅提升了能量利用率;2020 年,杨奎星[13]利用随机并行梯度下降模型(M-SPGD)算法对8 km 城市自由空间链路上的激光传输进行了实验,在D/r0=9.5的大气湍流下,FSO 系统接收端的耦合效率提升了约3.7 dB,使其在远程量子通信中得到了发展;胡琴涛[14]提出了一种ASPGD 算法利用动量和自适应的增益系数加快收敛速度,使迭代次数减少了50%,该算法对参数具有极强的鲁棒性,且可以避免陷入局部极值点。除了上述这些无模型优化算法,有模型的优化算法也拥有极大的应用价值。2018 年,单月[15]借助线性相位分集法将可变形镜的驱动电压和远场图像之间构建起线性模型,显著增强了AO 系统的成像质量;何旭[16]和崔莹[17]分别利用Martin 模型算法和JA (Jacopo Antonello)模型算法补偿低阶像差,用SPGD 算法校正高阶像差,成功恢复出原始光斑,从而验证了混合算法提升光纤耦合效率的可行性;任虹禧[18]对Lukosz 模型算法提出了改进,不仅使图像采集次数从原来的2N+1 减少到N+2,还大幅提升了扩展物体的成像分辨率。
然而这些算法都有一定的局限性:无模型算法虽然可以全频域校正波前像差,但是往往迭代数百次才会收敛,校正速率较低;而有模型算法虽然校正速度快,但是只能校正部分低阶像差,校正精度不够高。因此,为了能够同时获得高校正精度和快校正速率,本文提出了一种混合模型算法,利用像差先验知识改进传统的Lukosz 模型,对低阶Lukosz 模式像差进行评估和补偿,然后通过余弦衰减 (cosine_decay) 算子修正ASPGD 算法,进一步校正其余的高阶像差和低阶残差。
本文先通过数值仿真随机模拟出50 组Kolmogorov湍流功率谱下、大气湍流强度均是D/r0=5的波前畸变,然后分别采用SPGD 算法、ASPGD 算法和混合模型算法进行校正,并对仿真结果进行了定量的对比分析,最后在FSO 系统的光接收机端引入无波前传感自适应光学系统,应用混合模型算法对动态变化的畸变波前实施实时校正,通过实验验证了算法的有效性。混合模型算法对近地面光链路、地-空链路、空-地链路的无线光通信系统的通信性能的提升有一定的帮助。
2 理论推导
2.1 ASPGD 算法
SPGD 算法的基本思想是利用性能指标J的变化量∆J和控制电压u的变化量 ∆u进行控制电压的梯度估计,通过迭代的方式在梯度下降方向上进行控制电压的搜索[19],直至性能指标J搜索出极大值。而ASPGD 算法则是在SPGD 算法的基础上采用Adam算子[20]进行修正,突破了SPGD 算法在迭代初期搜索极其缓慢的局限性,获得了更高的校正效率。
如果对性能指标函数J的差值 ∆J进行泰勒近似并忽略掉高阶项,那么下降梯度增益gk可以近似表示成:
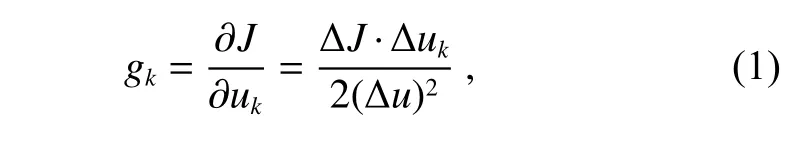
其中:∆uk=±∆u属 于随机生成的电压微扰项。应用Adam 算子对传统的SPGD 算法进行修正,则有:

对控制电压uk进行迭代更新,得到:
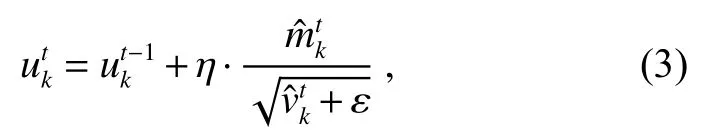
其中:η 是学习速率,它控制了权重的更新比率,η越大,那么初始的搜索速率越快,η 越小,那么最终的收敛性能会越好。ε是无穷小量,通常取10−8。
相比于SPGD 算法,ASPGD 算法的校正速率是它的2 倍,且对迭代步长的敏感度更低[14],校正精度也更高。尽管如此,ASPGD 算法盲搜索的迭代次数依旧需要上百次,其收敛时间理论上存在改进之处。
2.2 Lukosz 模型算法
Lukosz 多项式是Zernike 多项式的线性叠加,且具有导数正交的特性[21],因此前N阶Lukosz 模式的线性组合也可以完备地描述大气湍流产生的畸变波前:

其中:li是第i阶Lukosz 多项式Li的模式系数。
对于不包含倾斜项的波前像差,当评估第i阶Lukosz 多项式模式系数的校正量时,可以利用可变形镜向光学系统中分别添加偏移量为+biLi和−biLi的模式像差,然后测量相对应的系统评价函数分别为G+和G−,那么评价函数和模式系数之间将满足以下二次方程组的关系:
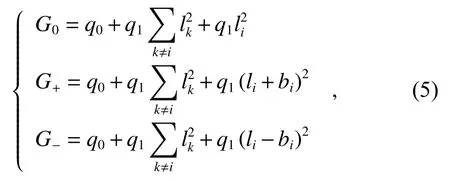
其中:G0是光学系统的初始评价函数,q0和q1都是与远场光斑图像相关的常数。借助抛物线函数的对称轴来估计最佳校正像差位置[22-23],联立方程组进行求解可以得到第i阶Lukosz 多项式的校正量li,correct应 该为:
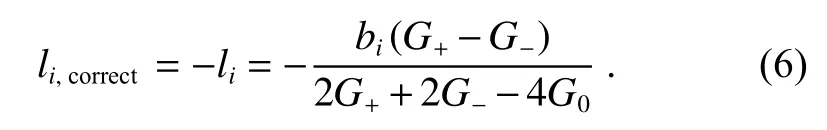
可以发现在每次迭代过程中,校正N阶Lukosz多项式的模式系数需要2N+1 次评价函数的测量。但是根据最优晶格的研究,晶格覆盖最多只能满足5 维[24],因此测量的时候只需要考虑前5 阶Lukosz模式的影响,即算法迭代一次需要测量11 次评价函数。
由于极少的测量可以换来波前畸变极大的提升,Lukosz 模型算法的校正速率极快,非常适合于短时间补偿起伏较小的像差,同时由于Lukosz 模型算法无法有效校正更高阶的模式像差,导致其校正精度受到了一定的局限。
2.3 混合模型算法
ASPGD 算法的学习速率η 如果太大将会导致迭代后期收敛速率的急速下跌,适当减小η 能够获得更好的收敛性能,因此可以采用cosine_decay 算子[25]控制学习速率的范围,通过余弦减小的方式来避开局部收敛区域,使最终的校正速率得到提升,这种改进的方法称为AcSPGD 算法。第t次迭代时的学习速率 ηt可以表示成:
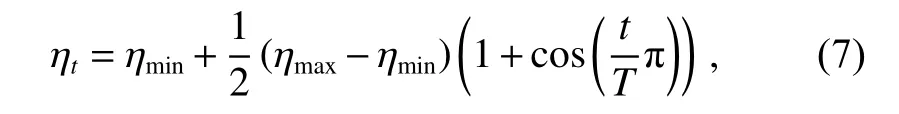
其中:T是算法的总迭代次数,被硬件条件所限制,ηmax和ηmin分别是人为设置的最大学习速率和最小学习速率。
此外,Lukosz 模型算法的校正精度受初始像差的均方根(RMS)和测量偏移量系数bi的影响极大[26-27]:如果初始像差很小,模型算法在较小的测量偏差下就可以获得最佳校正精度,但是当初始像差大于所给定的测量偏差时,评价函数的极值点就会偏离二次曲线搜索区导致算法局部收敛,倘若此时采用较大的测量偏差来校正,偏置曲线在边界区域的局部斜率又会产生较大的误差,不同模式之间的串扰就会降低像差系数的测量精度。因此,可以根据像差先验知识改变校正模式顺序,首先测量并校正前4~8 阶Lukosz 模式中较大的模式像差,减小系统中大像差之间产生的串扰,使评价函数与模式像差之间尽可能满足二次关系,然后用Lukosz 模型算法精确补偿剩余的小残差,这样有利于扩大测量偏移量的选取范围,避免二次曲线区域的失真,进而提升Lukosz 模型算法的校正精度,这种方法称为预校正模型算法。其中4~8 阶Lukosz模式中较大的模式像差的判断方法如下:
在预测第i阶Lukosz 多项式模式系数的校正量时,可以优先利用可变形镜向光学系统中分别添加评估偏移量为+eiLi和−eiLi的模式像差,然后测量相对应的系统评价函数分别为G+和G−,如果假设校正方向以评价函数越大越优,那么就选取比G0更大的添加方式作为该阶模式像差的初始校正,如果两种添加方式均不能使评价函数增大,说明该阶模式像差实际上较小,不需要提前添加较大的评估偏移量。
混合模型算法就是将以上两种改进的算法相结合来校正波前畸变的,首先利用预校正模型评估出一个较优的初始Lukosz 模式系数,对波前畸变的低阶像差进行初步校正,然后通过AcSPGD 算法对低阶残差和待校正的高阶像差进行补偿,这样既能够获得极快的起始收敛速度,又能够提升最终的校正精度。混合模型算法的流程图如图1 所示。
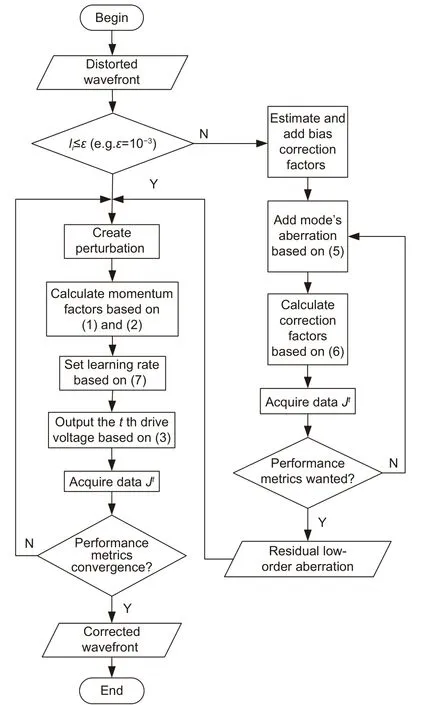
图1 混合模型算法流程图Fig.1 Flow chart of the hybrid modal algorithm
3 仿真结果
在Kolmogorov 湍流功率谱的条件下,利用前15阶Zernike 多项式随机生成20 个等距排列的大气相干长度为0.04 m 的湍流相位屏,其中前3 阶模式像差系数均设置为0,并通过多相位屏模型[28]模拟激光在大气中的传输过程,具体仿真参数如表1 所示。

表1 湍流大气传输数值仿真参数列表Table 1 System parameter settings in the simulation
选择Zernike 多项式系数作为校正目标,选择SR 作为系统评价函数,分别利用SPGD 算法、ASPGD 算法和混合模型算法校正湍流强度为D/r0=5的波前畸变,重复50 次实验减小偶然性,校正结果如图2 所示,图3 给出了其中一次混合模型算法校正时前4~15 阶Zernike 多项式系数的补偿结果。仿真时,Zernike 系数的扰动幅度均选取0.00038,SPGD 算法的增益系数 γ选取80000,ASPGD 算法的学习速率η选取0.01,混合模型算法的最大学习速率ηmax和最小学习速率ηmin分别选取0.02 和0.01,评估偏移量系数ei和测量偏移量系数bi分别选取2 和7。
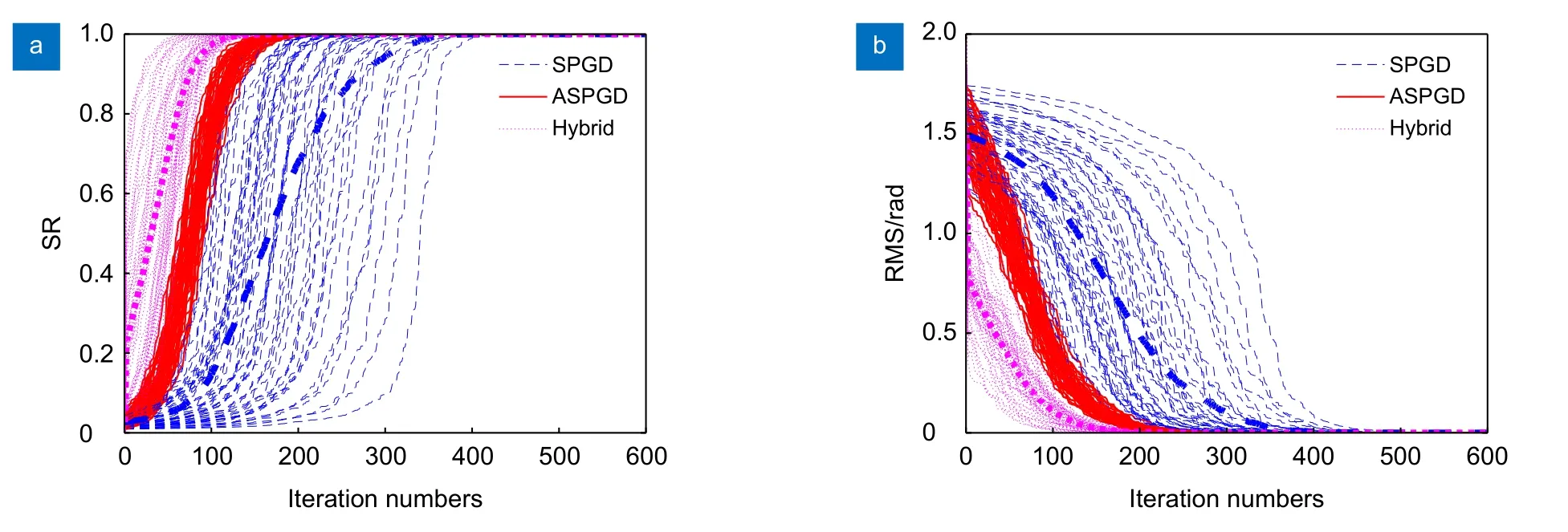
图2 不同算法校正结果对比图。(a) SR 变化曲线;(b) RMS 变化曲线Fig.2 Correction results of different optimization algorithms.(a) SR varies;(b) RMS varies
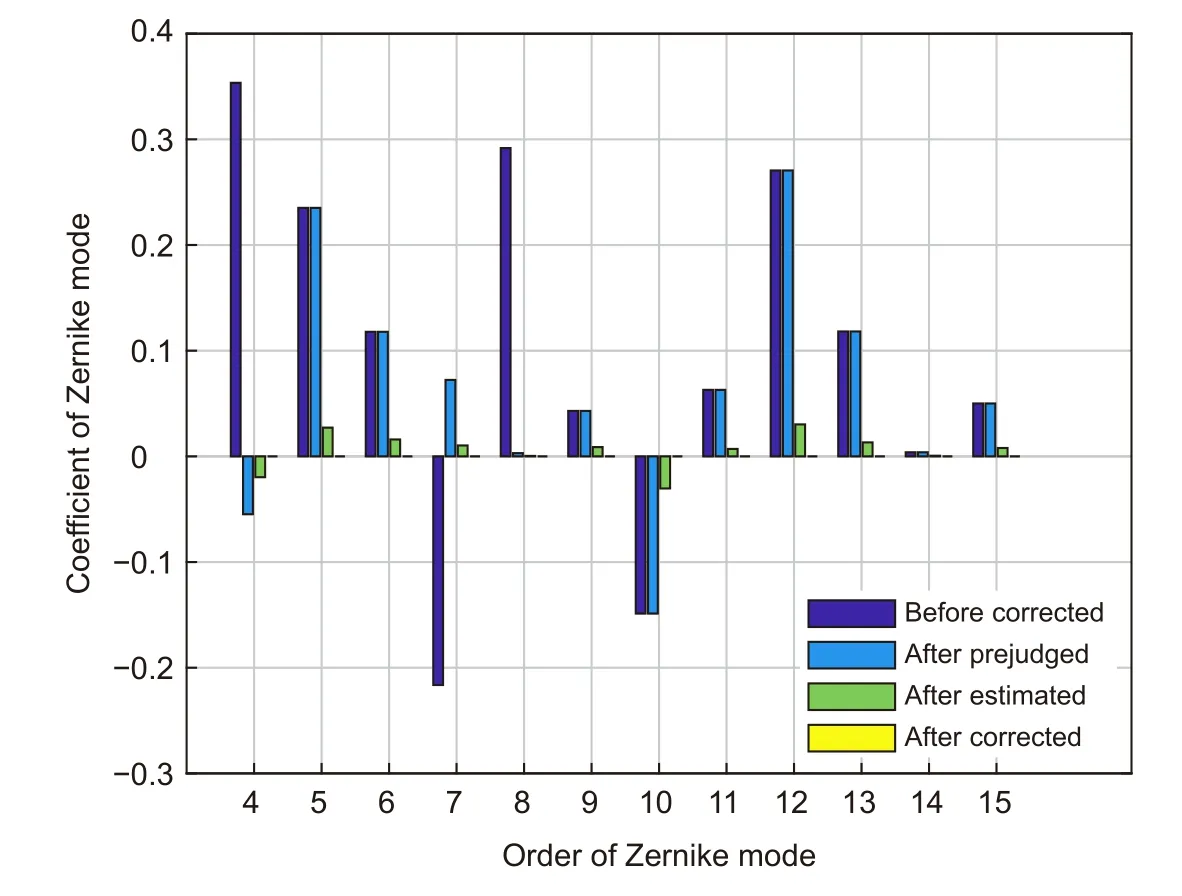
图3 混合模型算法校正前后Zernike 系数柱状对比图Fig.3 Histogram of Zernike coefficients between hybrid algorithm correction
图2 中三条粗线分别代表着三种算法的50 次校正结果的平均变化曲线:混合模型算法经过1 次大像差评估后,第4、7、8 阶Zernike 模式像差得到了有效的初次校正,此时SR 从0.03 提升到0.05,RMS也相应从1.51 rad 减小到1.43 rad,然后再借助Lukosz 抛物线模型估测最佳校正偏移量,经过2 次迭代,前4~15 阶Zernike 模式像差均有所减小,SR从0.05 迅速提升到0.23,RMS 也从1.43 rad 大幅减小到0.77 rad,表明预校正模型有助于缩小横向搜寻区域,提升算法的收敛速度;忽略不同算法计算量的差异从收敛时间上来对比,混合模型算法、ASPGD算法和SPGD 算法的迭代次数分别达到了119 次、169 次和351 次,说明混合模型算法的收敛速率大约是ASPGD 算法的1.5 倍,是SPGD 算法的3 倍,同时也验证了文献[9] 中ASPGD 算法的校正速率是SPGD 算法的2 倍的结论。
4 实验验证
本文搭建了一套无波前传感自适应光学实验系统进行算法验证,实验系统如图4 所示,主要由1550 nm 激光光源、光扩束系统、静相位屏、可变形镜和红外相机组成。其中,LEXITEK 静相位屏的光窗直径为100 mm,内部光程差范围在5 μm~30 μm,能够产生相干长度为3 cm 的大气湍流,相位分布满足Kolmogorov 湍流理论;DMP40 可变形镜是美国Thorlabs 公司旗下具有40 个可驱动单元的压电式变形镜,光瞳直径为1 cm,响应频率为2 kHz,可以通过前15 阶Zernike 多项式系数或者40 个促动器单元的分段电压来直接控制镜面面型。
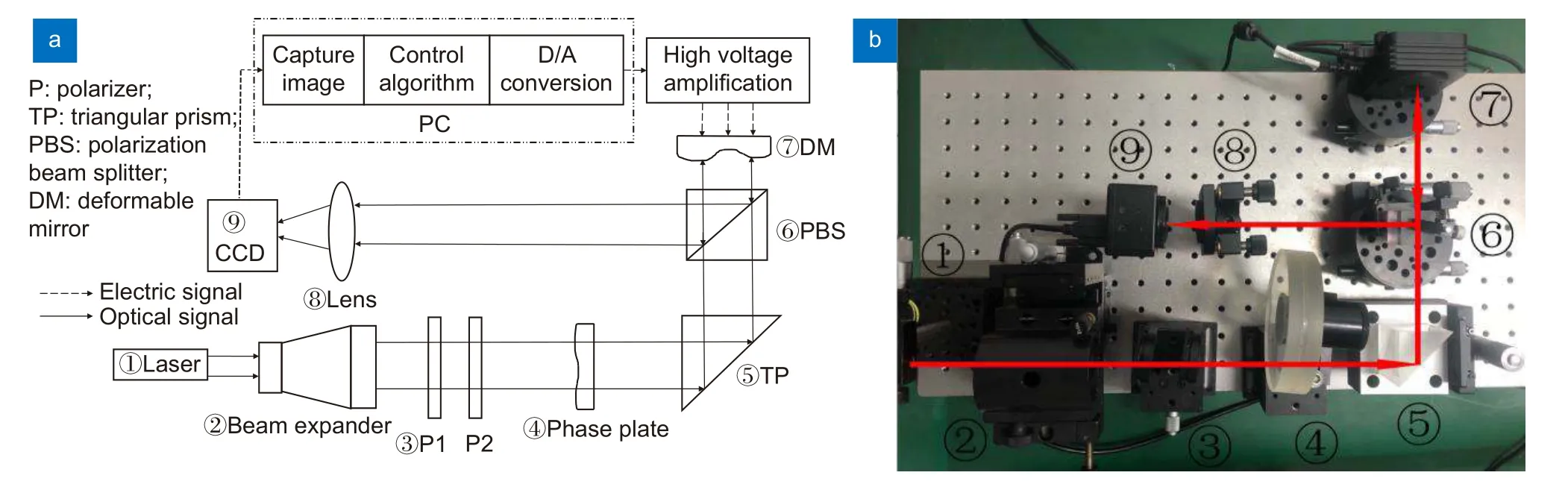
图4 无波前传感自适应光学系统。(a) 原理图;(b) 实物图Fig.4 The wavefront sensorless adaptive optical system.(a) Schematic;(b) Experiment
在图4(a)的原理图中,实线表示光信号路径,虚线表示电信号路径。由1550 nm 激光器发出的基模高斯光束先通过扩束镜扩束6 倍,接着通过偏振片组降低光强避免接收端的相机采样过曝,再经过静相位屏产生随机相位畸变,然后经过三棱镜的反射垂直入射到可变形镜的镜面上进行波前校正,最后反射光经过分光棱镜的反射后被焦距为50 mm 的凸透镜聚焦,接收端采用红外相机采集远场光斑,并通过混合模型算法处理图像信息,实时产生迭代的驱动电压来控制可变形镜的镜面,从而实现无波前传感自适应光学系统的闭环校正。实物图如图4(b)所示。
实验中,随机采集远场光斑图像,将像清晰度函数作为系统的评价函数,即图像像素的归一化矩阵的平方和,并利用SPGD 算法和混合模型算法分别校正波前畸变,光斑的光场分布如图5 所示。
从图5 可以看出,校正前的远场光斑受静相位屏散射的影响较大,光强分布弥散不均匀,而校正后的光斑半径更小、能量更集中,形状也更接近于圆形。远场光斑沿纵轴方向的光场分布如图6 所示。

图5 远场光斑光强分布图。(a) 叠加随机像差;(b) SPGD 算法校正后;(c) 混合模型算法校正后Fig.5 Captured intensity of the far-field spot.(a) Before corrected;(b) Corrected by the SPGD algorithm;(c) Corrected by the hybrid algorithm
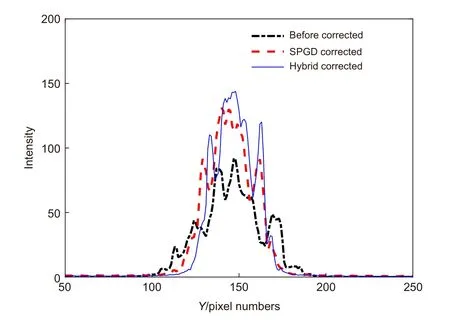
图6 远场光斑光强纵向分布图Fig.6 Fitted intensity of the far-field spot on the horizontal axis
利用最小二乘法对远场光斑的光场分布进行高斯拟合,通过计算可知经过SPGD 算法和混合模型算法校正后,远场光斑的半高全宽从42 pixels 分别减小到30 pixels 和25 pixels,峰值光强也从73.1 分别增加到131.3 和154.3,SR 大约提升了2 倍,结果表明混合模型算法比SPGD 算法的校正效果更优。
将迭代次数作为横坐标,远场光斑的归一化平均光强作为纵坐标,分别画出SPGD 算法和混合模型算法在校正过程中评价函数的变化曲线对比图,如图7所示。从图中可以发现,混合模型算法和SPGD 算法分别在迭代28 次和84 次以后逐渐趋于收敛,表明混合模型算法收敛速率大约是SPGD 算法的3 倍;此外比较两种算法的收敛极值,远场光斑归一化光强分别从初始的347 增加到了583 和561,表明混合模型算法比SPGD 算法的校正精度要更高,这些结论都与仿真结果相符。倘若比较两种算法的初始校正速率,以像清晰度函数校正到500 为目标,它们需要的迭代次数分别为5 次和67 次,表明混合模型算法的初始校正速率大约是SPGD 算法的13 倍,这为大气激光通信实验中需要快速实时地校正波前畸变提供了帮助。
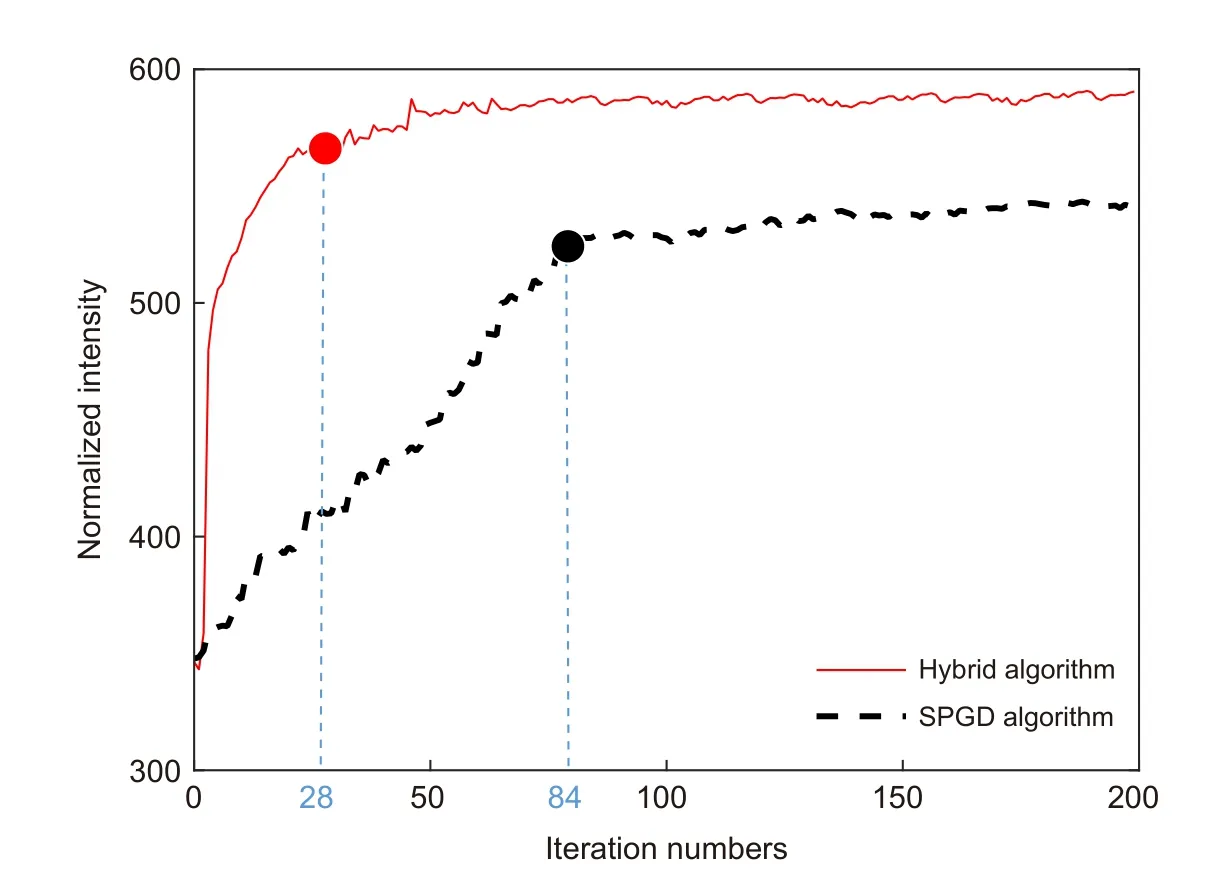
图7 评价函数的变化曲线对比图Fig.7 Improvement of normalized intensity for different algorithms
图8 是基于NRZ-OOK 调制的室内大气激光通信实验的原理图。在发射端,借助误码仪作为信号源来生成调制速率为20 MHz、数据码型为231-1 的随机码,并将其作为激光驱动电路的基带信号驱动半导体激光器发出1550 nm 激光光束。携带调制信号的基模高斯光束先经过扩束镜扩束6 倍,接着通过转速约15 r/m的旋转相位屏产生D/r0=0.8的随机畸变,最后被无波前传感自适应光学系统实时校正波前像差。在接收端,采用APD 和跨阻放大电路将探测到的光强信号转换成电压信号,借助示波器就可以观察到实时传输的信号波形,实验中采集到的20 MHz 方波信号的波形如图9 所示;以5 MHz 为间隔改变调制信号的传输速率,可以得到校正前后误码率随调制速率的变化曲线,如图10 所示。
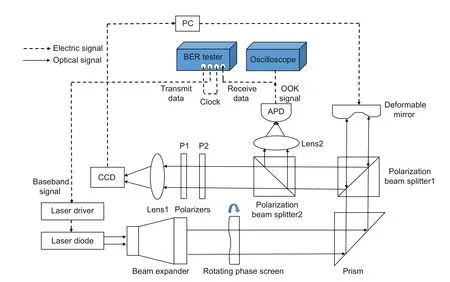
图8 大气激光通信实验光路图Fig.8 Experiment of data transmission in atmospheric laser communications
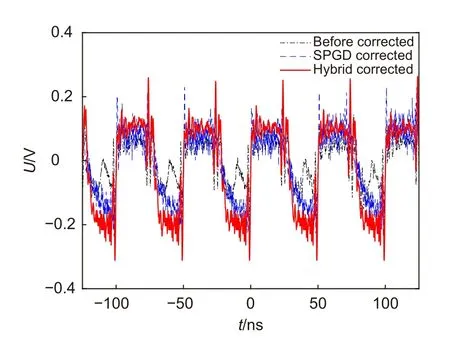
图9 大气湍流传输实测波形Fig.9 Waveform measured in atmospheric turbulence
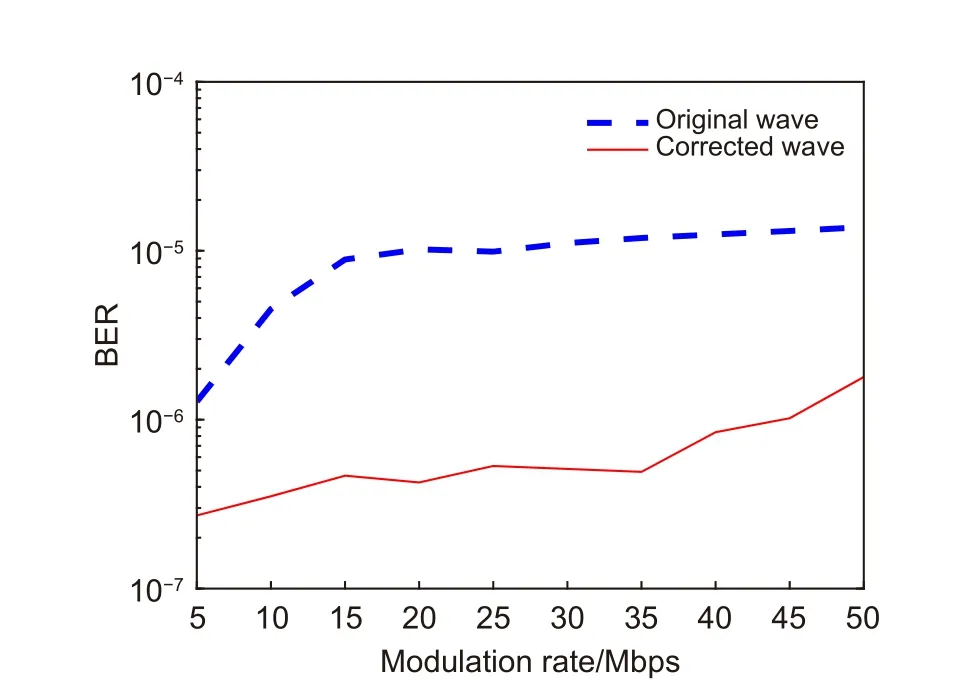
图10 误码率随调制速率的变化曲线Fig.10 Variation curve of BER with modulation rate
经过SPGD 算法和混合模型算法的优化后,20 MHz 方波信号的信噪比从30.5 dB 分别提升到了33.2 dB 和33.4 dB,表明混合模型算法能够获得更高的信噪比。而2.9 dB 的性能提升能够使大气激光通信系统的传输误码率从10−5降低到10−6,对于50 Mb/s内的自由空间光通信系统,混合模型算法均能够有效改善其通信性能。无波前传感自适应光学系统的校正带宽受红外相机采样频率的限制,同时可变形镜促动器影响函数模拟各阶Lukosz 模式像差时也存在拟合误差,这些都会影响到最终的校正效果。且本文仅从光学信号的处理角度研究了光信号传输特性,若要提升通信系统整体性能,还可以增加向前纠错的措施来达到更高速率、更低误码的通信要求。
5 结 论
本文提出了一种应用于无波前传感自适应光学系统的混合模型算法,以补偿大气湍流造成的像差畸变,采用Lukosz 预校正模型和AcSPGD 算法分别校正了低阶和高阶像差,并提升了迭代算法的校正精度和收敛速度。实验结果表明,混合模型算法的收敛速度是传统的SPGD 算法的3 倍,且可以获得更高的信噪比;将该算法应用在50 Mb/s 的大气激光通信系统中,系统误码率下降到10−6,通信质量有了较大改善。

