基于门控循环单元神经网络的LED寿命预测方法
龚晓春,朱 云,李 晟,颜建堂,李玉晓
(1.江西理工大学理学院,江西 赣州 341000,2.深圳卡洛照明有限公司,广东 深圳 518012)
引言
发光二极管(Light-emitting Diode, LED)是电致发光的半导体器件,具有长寿命、高能效、环保等优点,已被广泛应用于医疗、通信、照明等行业。但LED仍面临着器件可靠性、安全性和可用性保障的问题,限制了LED健康管理技术的发展。例如,LED的寿命预测是LED健康管理的关键问题,但现行的寿命预测方法存在准确性低且预测算法耗时较长等问题[1,2]。因此,如何提高LED寿命预测方法的准确性和寿命预测速度具有重要的研究意义。
当前的LED寿命预测方法可分为基于物理模型的方法和基于数据驱动的方法两类[3,4]。基于物理模型的方法首先需要分析LED退化或损坏行为的物理机理,再建立对应的退化模型。但是LED的寿命退化过程受多种因素的影响,导致物理机理分析精确度不高,且对测量数据有较高的要求,这些问题限制了这类方法被广泛应用[5]。基于数据驱动的方法是通过对采集到的退化数据进行分析和挖掘,无需构建LED的物理失效模型即可预测LED的寿命。因此,数据驱动法已成为LED寿命预测研究的热点。北美照明工程学会提出的IES TM-21-11标准[6]推荐了一套基于数据驱动的LED寿命预测方法。方法通过采集LED的流明维持数据,利用指数回归模型和非线性最小二乘(NLS,Nonlinear Least Square)回归方法建立流明维持数据衰退曲线,当流明维持数据衰减至70%时,则认为LED失效。该方法被广泛应用于生产制造过程,但是该方法提供的寿命信息单一且准确性不高[7]。为此,Fan等[8]针对大功率白光发光二极管,通过采集的流明维持数据,利用基于一般衰减路径模型的衰减数据驱动方法进行预测与IES TM-21-11推荐方法相比,可以获得更多的寿命信息和更准确地预测结果。但该方法只能预测一个批次LED的平均寿命,无法预测单个LED的寿命。
随着机器学习的快速发展,各种基于机器学习的数据驱动方法成为当前的研究热点,并被广泛应用于不同领域的寿命预测过程[9,10],取得了较好的效果。Lu等[11]提出利用温度、电流、初始色度坐标和初始光通量数据作为训练样本,通过改进的AdaBoost算法优化BP网络,从而预测LED的寿命。黄苏丹等[12]提出了一种多应力条件下的LED寿命快速评估模型,通过自适应遗传算法获得模型参数,实现了LED寿命的预测。以上方法虽然都能够实现LED数据的寿命预测,但是均未考虑LED寿命数据间存在时间依赖性,使得LED退化信息丢失,导致寿命预测准确性不足。
循环神经网络(RNN,Recurrent Neural Network)对时序数据具有出色的建模能力,能处理长度可变的时间序列并通过循环结构处理不同时刻的特征信息,适用于描述LED的退化过程[13]。但RNN在训练过程中容易出现梯度爆炸、梯度消失问题,难以解决LED退化数据的长依赖关系,这些问题限制了RNN在LED寿命预测中的应用。Hochreiter等[14]在RNN的基础上,提出了长短期记忆循环神经网络(LSTMRNN,Long-short Term Memory Recurrent Neural Network),在一定程度上解决了RNN的梯度爆炸和梯度消失的问题,但是LSTM单元结构复杂,导致预测速度较慢。Zhou等[15]利用LSTMRNN方法对LED的辐射功率数据进行LED寿命预测,与IES TM-21-11的方法相比,该方法的寿命预测误差更小,但是该方法将LSTMRNN的输入层输入数据长度设置为常数,因此在预测过程中考虑的LED历史退化信息有限。
相比于LSTM,门循环单元(Gate Recurrent Unit, GRU)神经网络[16-18]结构更为简单,训练收敛速度快,能够大大降低计算复杂度,有效提高LED寿命预测的效率。为此,本文提出一种基于门控循环单元神经网络的LED寿命预测方法,利用GRU特有的加权平均记忆结构简化了预测模型。同时,方法将模型输入数据的长度设置为变量,使预测过程考虑更多的LED历史退化信息,从而提高预测的准确性和预测速度。为了验证本文方法的有效性,通过退化实验采集了JUIFEI 3030 LED的流明维持数据,利用本文方法进行寿命预测,并与其他三种方法进行了对比分析。实验结果表明,相比于其他方法,本文方法具有更高的准确性和预测速度,同时还具有良好的鲁棒性。
1 原理与方法
1.1 门控循环单元神经网络
GRU是LSTM的变体之一,其内部激活函数包括sigmoid函数和tanh函数,其结构如图1所示。可见与LSTM相比,GRU简化了单元的门结构,降低了计算复杂度。

图1 GRU结构图Fig.1 The structure of GRU


(1)
其中,wr和wz分别表示rz和zt的权重向量,br和bz分别表示rt和zt的偏置向量。σ(·)表示sigmoid函数,*表示矩阵相乘运算。
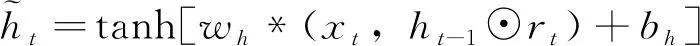
(2)

则t时刻神经元的细胞状态ht可以表示为
(3)
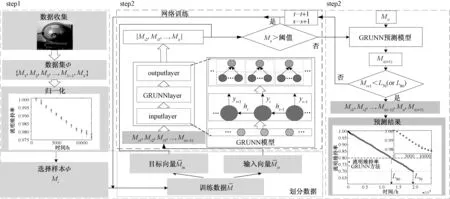
图2 LED寿命预测方法框架Fig.2 Framework of LED lifetime prediction
1.2 基于GRUNN的LED寿命预测方法
本文提出了一种基于GRUNN的LED寿命预测方法,GRUNN为多对多模型,即模型的输入序列和输出序列的长度相等。其中,ht-1表示t-1时刻GRU单元的状态。将ht-1和目标向量作为t时刻GRU单元的输入,即可计算出t时刻的输出yt和状态ht。利用实测LED流明维持数据构建训练集,训练GRUNN预测模型,再利用训练好的模型预测LED未来的退化行为。方法的流程图如图2所示,方法的具体步骤如下:
步骤1:建立流明维持数据集。

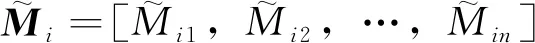
b)对原始流明维持数据进行归一化预处理。因为流明维持数据是衰退数据,归一化方法如下:

(4)

则N个同一批次的LED样本的归一化流明维持数据,用集合Φ={M1,M2,…,MN-1,MN}表示。其中,第i个LED样本的归一化流明维持数据向量可表示为Mi=[Mi1,Mi2,…,Min],i=1,2,…,N。
c)构建GRUNN模型的训练样本。

步骤2:利用训练样本训练GRUNN寿命预测模型。


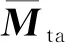
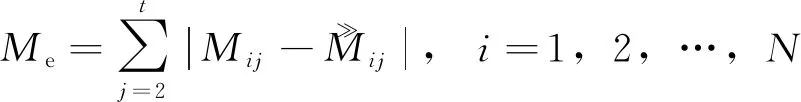
(5)
若Me大于设置的阈值,则利用Adam[19]算法将误差梯度方向传播至GRUNN的输入层,不断寻找网络参数的最优解,直至Me小于设置的阈值。当网络训练完毕,得到第Mit步GRUNN寿命预测模型。
步骤3:预测第i个LED的寿命。将最后一个流明维持数据Mit作为输入,输入至步骤2得到的第s步GRUNN寿命预测模型的输入层,模型即可预测并输出t+1时刻的流明维持数据Mi(t+1)。若Mi(t+1)流明维持数据还未退化至初始归一化流明维持数据Mi1的70%(或80%),则令t=t+1,s=s+1返回至步骤1,继续训练新的GRUNN预测模型,并重新预测Mi(t+1)时刻的流明维持数据Mi(t+1)。若Mi(t+1)流明维持数据已退化至初始归一化流明维持数据Mi1的70%(或80%)以下,则绘制第Li70个LED的寿命退化曲线,并输出预测寿命Li70(或Li80)。
2 LED流明维持数据采集方法
为了收集能表征LED性能退化的流明维持数据,利用如图3所示的流明维持数据采集装置进行数据采集。

图3 退化实验设备实物图Fig.3 The diagram of degradation experimental equipment
将LED样本放置在如图3(a)所示的积分球中,环境控制设备、光电快速测量系统及驱动电源集成在如图3(b)所示的柜机中。其中,直流电源为积分球供电;积分球采集到LED样本的流明维持率数据,通过光纤传输给光电色快速测量系统;光电色快速测量系统将流明维持数据上传至上位机进行存储和分析;环境控制系统可监控和设置温湿度等环境参数。
采集流明维持数据需要设置的环境参数包括LED样本的壳体温度、环境温度、驱动电流和测量电流,从0 h开始,流明维持数据每1 000 h采集1次。
3 LED寿命预测实验与分析
利用本文提出的方法对JUIFEI 3030 LED进行寿命预测实验。实验数据从0 h开始,数据总时长为0~12 000 h,因此每个LED样本的流明维持数据个数为13。LED测试环境参数设置如表1所示。
实验对JUIFEI 3030 LED进行寿命预测,预测结果分别与利用NLS回归方法、基于RNN的预测方法和基于LSTMRNN的预测方法进行对比分析。

表1 测试环境参数设置
3.1 LED寿命预测结果的评价指标
为了评价不同方法预测结果的准确性,文献[8]中提出将同一批次20个LED的期望寿命LE作为参考寿命,通过对比预测结果和参考寿命间的误差即可评价方法预测的准确性。
LE的计算方法具体步骤如下:
步骤1:根据IES TM-21-11标准提出的LED衰退模型如式(6)所示:
Γ(t)=βexp(-α·t)
(6)
其中,Γ(t)表示t时刻的平均归一化流明维数数据,β表示投影初始常数,α表示衰减速率常数。
将同批次20个LED样本的流明维持数据归一化,然后根据IES TM-21-11标准的数据点选取规则,利用NLS方法拟合式(6)得到参数α和β,并外推式(6)计算得到20个LED样本基于NLS方法的预测寿命Lk,k=1,2,…,20。
步骤2:分析该批次LED样本的寿命服从的分布函数。假设某批次LED样本寿命服从威布尔分布,正态分布和对数正态分布。然后,对比三种分布,确定该批次LED寿命最可能服从统计分布。确定方法如下:
a) 利用最大似然估计得到三种分布函数的参数,参数估计可以表示为:

(7)

b) 将分布函数参数的最大似然估计代入三种分布函数中,再利用贝叶斯信息准则(Bayesian Information Criterions,BIC)[20]评价三种分布对LED寿命的拟合效果,BIC值越小则拟合效果越优。BIC评价的表达式为:
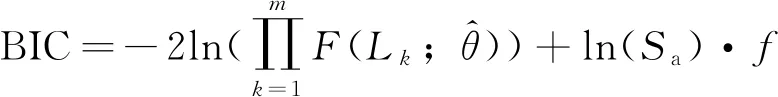
(8)
其中,f表示分布函数的参数个数;Sa为样本总数。
c)利用确定的最优分布函数,计算期望寿命作为参考寿命评价指标,期望寿命LE的表达式为:
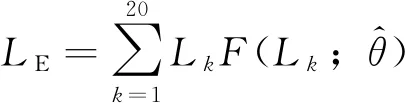
(9)
本文将L80和L70期望寿命分别用LE80和LE70表示。
步骤3:方法的预测准确性评价。为了进一步对比不同的寿命预测方法准确性,本文在文献[8]的基础上提出采用以下两种方法进行预测结果准确性评价。
a) 通过计算预测寿命与期望寿命之间的百分数误差Serror衡量方法的准确性,Serror越小则预测结果越准确;否则,预测结果越不准确。Serror的表达式为:
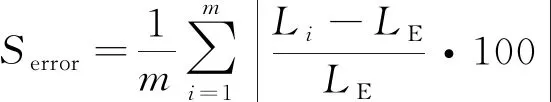
(10)
其中,m表示寿命预测实验的次数,Li表示第i次实验预测得到的预测寿命。
b)对预测的LED流明维持数据与实测流明维持数据进行误差分析,第t个数据点的误差用Mte表示,其表达式为:
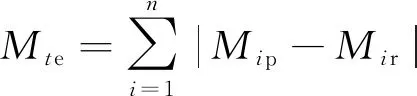
(11)
其中,n表示实测的数据点总数,Mip表示预测的第i个流明维持数据,Mir表示实测的第i个流明维持数据,Mte越小则表示该数据点的预测越准确。
3.2 LED寿命预测结果与讨论
利用1.2节中的方法,对JUIFEI 3030 的同一批次中的第i个LED进行寿命预测实验。实验过程如下:
步骤1:利用3.1节的方法计算该LED的期望寿命。

其次,分别假设该批次的LED寿命服从威布尔分布、正态分布和对数正态分布。利用式(7)分别估计LED的L80和L70寿命的3种分布函数的具体表达式。再利用式(8)对3种分布函数进行评价,评价结果见表2。根据BIC评价标准,由表2可知该批次的20个LED寿命应服从对数正态分布,分布函数如式(12)所示:

(12)
其次,L80寿命服从的分布函数参数为σ=0.0869,μ=11.7478;L70寿命服从的分布函数参数为σ=0.0886,μ=12.2204。

表2 三种统计分布的BIC值
最后,利用式(9)计算L80和L70的期望寿命为LE80=126 948 h和LE70=203 692 h,即L80和L70的参考寿命。LED寿命曲线以及L80和L70寿命服从的对数正态分布曲线,如图4所示。
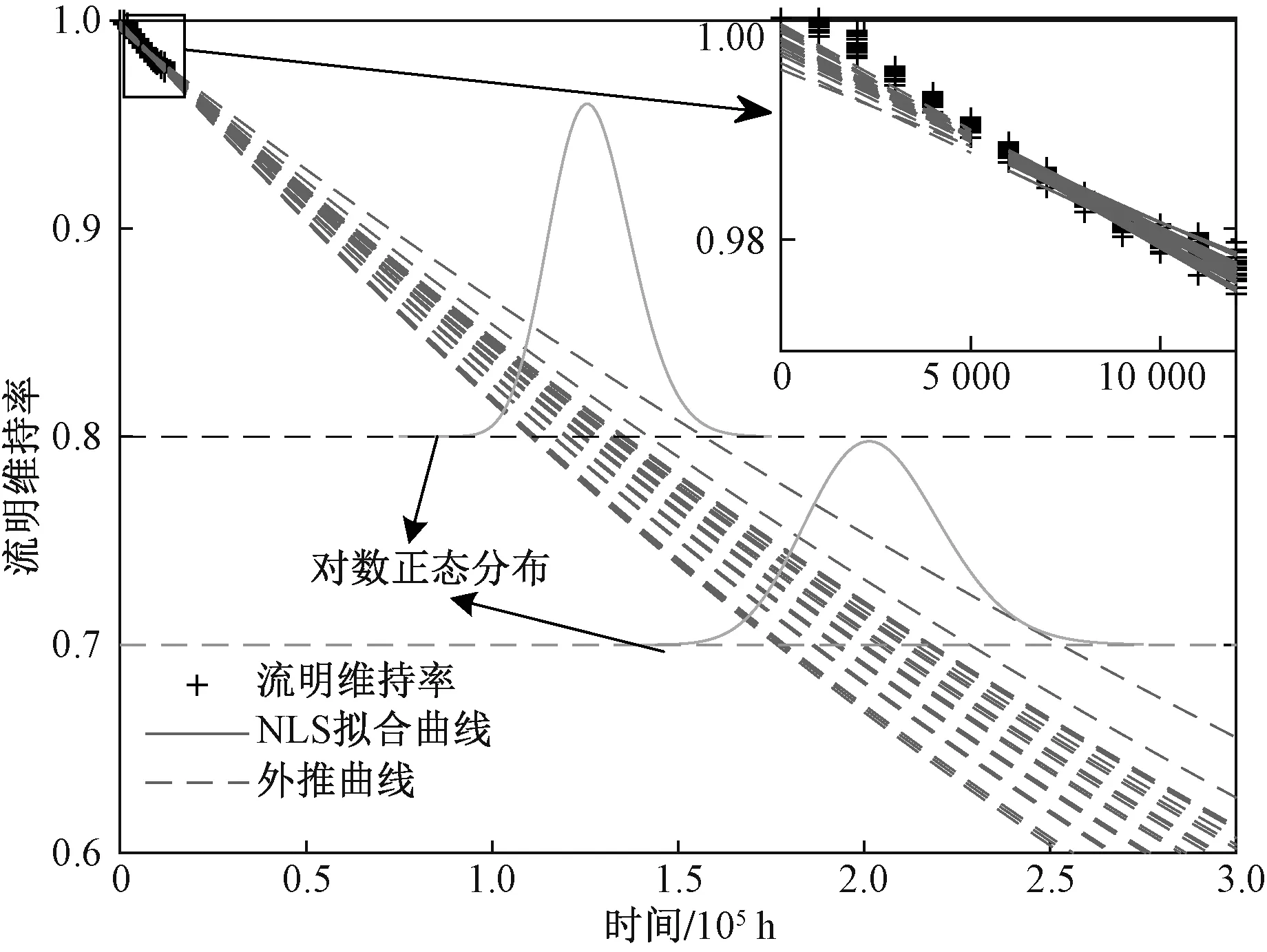
图4 20个LED的退化曲线及寿命分布Fig.4 Degradation curve and lifetime distribution of 20 LEDs

为了测试方法的鲁棒性,改变GRUNN输入数据的长度,以检验方法在考虑不同长度历史信息时的预测效果。利用本文所提方法,分别令t=7,8,9,10进行LED的寿命预测。为了检验本文方法的先进性,同时分别利用基于NLS、基于RNN和基于LSTM的LED寿命预测方法进行对比实验。不同方法得到的寿命退化曲线如图5所示。
通过式(10)计算四种方法预测寿命的百分数误差Serror,同时分析了RNN方法、LSTMRNN方法和本文方法预测花费时间,如表3所示。
由表3可以知,从不同起始时刻开始预测,即t=6,7,8,9,10时,本文方法预测L80和L70寿命的百分比误差Serror均是所有方法中最小的,预测准确性最高,且具有良好的鲁棒性。IES TM-21-11标准提供的NLS方法得到的L80和L70预测寿命的预测准确性最差。
分析其原因,是因为相比于LSTM,GRU拥有独特的过去记忆和当前记忆的加权平均结构,可以更快速且有效地学习LED的历史退化信息。而NLS方法的LED衰退模型单一,不能表征所有类型LED的衰退行为。
在三种基于循环神经网络的方法中,RNN的预测误差最大,预测准确性最差。这是因为RNN没有单独记忆单元或者是记忆结构,无法在学习LED退化历史信息中有效记录退化信息。LSTMRNN方法的预测准确性优于RNN,但劣于GRUNN。这是因为,虽然LSTMRNN拥有记忆单元学习LED历史退化信息,但是其结构复杂,增加了计算的复杂度,对小样本数据的LED增加了记忆的不确定性。
另一方面,由表3可知,本文所提方法比LSTM方法的预测速度更快。需要指出的是,虽然RNN的结构比GRU和LSTM都更简单,但预测所花费的时间却并没有优势。分析其原因是RNN在学习LED的衰退过程时,长期的衰退信息会被短期的衰退信息所覆盖,导致网络收敛速度较慢。
为了进一步验证本文方法的有效性,利用式(11)分别计算4种方法的预测数据与实测数据点间的误差,如表4所示。本文方法的所有预测数据点和实测数据点间的误差总和为0.0307,是4种方法中最小的。由误差分析进一步证明了本文所提出的方法在预测LED的寿命时,具有较高的准确性。

图5 实验寿命预测结果图Fig.5 The experiment 1 lifetime prediction results chart
4 结论
本文提出了一种基于门控循环单元神经网络的LED寿命预测方法,该方法利用GRU的加权平均记忆结构构建了循环神经网络模型,并将GRUNN模型输入层设置为变量,使得预测模型可以考虑任意长度的LED历史退化信息,从而有效捕捉流明维持数据中的时间依赖性,可以更加快速准确地预测LED的寿命。本文通过实验验证了所提方法的有效性和先进性,通过退化实验收集LED流明维持数据,并对JUIFEI 3030 LED进行寿命预测实验,实验结果验证了本文方法具有很好的准确性和鲁棒性。对比实验的结果还表明,本文方法在所有对比方法中具有最好的预测精度和最快的预测速度。本文方法可以应用于LED的可靠性分析和健康管理过程,具有较大的推广价值。

表3 四种方法的预测结果
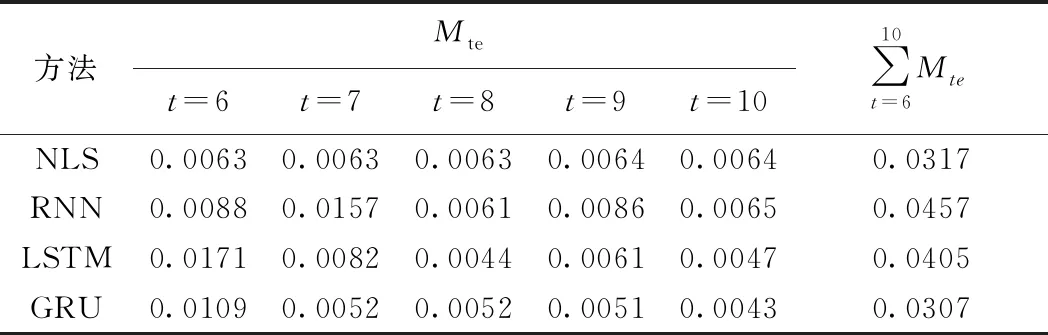
表4 预测已归一化的流明维持数据误差

