考虑土体参数不确定性的供水管道地震响应分析

李锦强，钟紫蓝，史跃波，韩俊艳，侯本伟

(城市与工程安全减灾教育部重点实验室(北京工业大学)，北京 100124)

历次地震灾害调查和研究表明[1-4]，强烈地震后的埋地供水管道将遭受极大的损害和破坏，乃至功能彻底丧失，进而引发火灾、停电断水等一系列次生灾害，严重影响了城市的震后抢修工作，对社会造成了巨大的生命和财产损失[1-4]。承插式供水管道的破坏形式主要包括管道节点(接口)破坏、管身破坏(裂缝、折断等)、连接处破坏(弯头、三通等)[4-6]。对于直埋管道，主要破坏现象为管道接口拉压破坏，而复杂的三通、四通接口处主要表现为弯曲破坏，因此，接口破坏是埋地管道震害最主要、最常见的破坏形式，也是城市地下供水管网抗震的薄弱环节。

埋地管道在敷设过程中不可避免地穿过不同地质条件的场地，管道周围土体为非均质且土体力学参数存在一定变异性，直接影响埋地管道的地震响应。对于土体参数不确定性对地震响应的影响，国内外学者开展了相关的研究工作。Phoon等[7]将土体的固有变异性模型转化为一个随机场，其变异系数及波动尺度均由实验室试验结果确定，详细说明了土体参数的相关性考虑方法。Jin等[8]在研究地震作用下土-结构相互作用响应时考虑了土体参数不确定性的影响，结果表明，土体参数不确定性对土-结构相互作用体系谐振频率附近的模态响应传递函数影响显著。Yoon等[9]以API 5L X65埋地天然气管道为研究对象，通过一次二阶矩方法研究了土体参数变异性对埋地管道非线性地震响应的影响，结合增量动力分析(incremental dynamic analysis, IDA)方法研究了结构峰值应变随地震动强度的变化规律，并建立了以峰值加速度(peak ground acceleration, PGA)为地震动强度指标(intensity measure, IM)，峰值应变为结构损伤指标(damage measure, DM)的易损性曲线，结果表明，内摩擦角和土体重度的变异性会对易损性分析结果产生显著影响。Wijaya等[10]采用OpenSees建立了埋地灰口铸铁管道-土体相互作用简化模型，考虑土体参数间的相关性和土体参数的空间变异性，研究了土体参数变异性和行波效应对概率地震需求分析的影响，建立了每公里修复率以及峰值地面应变之间的概率地震需求模型。Gallage等[11]基于OpenSees平台研究了土体重度、土体内摩擦角这两个参数的不确定性对分段管道地震动力响应的影响，提取了不同参数影响下的不同时刻接口张开量以及地震动全周期最大接口张开量，通过对比发现土体重度的不确定性对于接口张开量的影响要小于内摩擦角。禹海涛等[12]以某盾构隧道为研究对象，基于随机场理论建立描述地层参数空间变异性和相关性的随机场模型，并开展考虑地层参数随机场影响的隧道纵向地震响应多工况模拟。研究发现，考虑随机场可使隧道结构弯矩响应幅值放大约80%，将导致结构设计偏于不安全。Chen等[13]以港珠澳大桥海底隧道结构为研究对象，考虑土体参数的变异性和行波效应的影响，发现土体参数的不确定性对于沉管隧道接口处的轴力和GINA止水带的变形影响显著。张晋彰等[14]基于随机场理论，以土体弹性模量的空间变异性为切入点，采用蒙特卡罗方法和有限差分模拟计算相结合的方法，开展了隧道水平收敛的随机分析，提出了可以把空间变异性研究应用到实际工程的参数折减法、放大系数法和可靠度分项系数标定法。

以上诸多学者采用数值模拟方法对地震作用下埋地管道、盾构隧道等长线性结构响应进行了研究，土体参数不确定性也引入到部分研究中。然而，土体参数不确定性对于分段式管道接口响应规律的工作开展还不够全面，对于埋地球墨铸铁供水管道的研究更为不足；另外，已有的研究[9-11]仅考虑了土体重度、内摩擦角两个土参数的不确定性，实际工程研究中仍有其他土体参数的不确定性需要进一步考虑。针对目前研究的不足，采用3条不同抗震设防烈度下的人工合成地震动作为管道-土体相互作用模型的非一致地震激励输入，考虑管道安装不规范、管道老化锈蚀等因素引起球墨铸铁管道局部接口抗拉强度折减，揭示土体重度、内摩擦角、黏聚力和土弹簧屈服位移4个关键不确定性参数对服役期间埋地球墨铸铁供水管道地震响应的影响规律。

1 球墨铸铁供水管道模型

1.1 数值模型介绍

本研究开展的工作均基于OpenSees有限元平台[15]，球墨铸铁供水管道系统由100根管段连接而成，每段管道长6 m，共有99个接口，如图1所示。由于球墨铸铁管道本身刚度远大于管道接口刚度，地震作用时管道接口处的变形和转角远大于管道本身，可将管道简化为弹性地基梁，管道间的接口采用接口弹簧进行模拟，其简化力学模型基于已开展的球墨铸铁管道轴向拉伸力学性能试验结果简化而成[16]，如图2所示。管-土相互作用采用土弹簧进行表征，土弹簧的获取(式(1)、(2))参照美国生命线联盟(American Lifelines Alliance, ALA)规范[17]，土弹簧简化双折线模型如图3所示。已有研究表明[18-19]，地震动对埋地直管道的轴向响应较大，弯曲向响应远小于轴向响应，可忽略不计，因此，只考虑管道轴向方向的地震动输入，地震动时程在土弹簧底部输入。该模型的其他介绍及正确性验证可参考以往研究[16,20-22]。

图1 管道-土体相互作用数值模型示意

图2 球墨铸铁管道接口简化模型

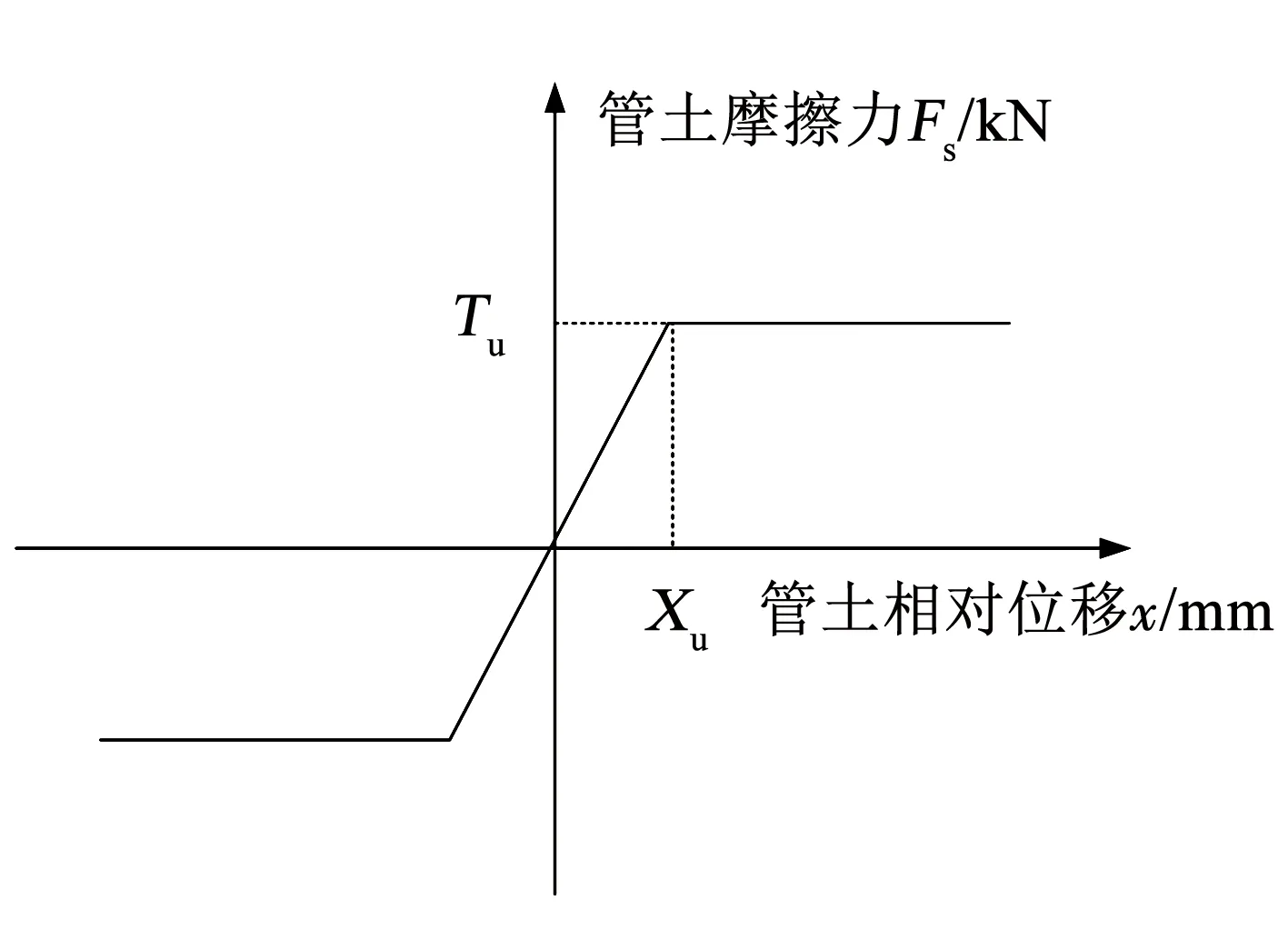
图3 轴向管-土间相互作用弹簧

(1)

(2)

式中：D为管道直径，H为管道埋深，γ为回填土有效重度，c为回填土黏聚力，φ为内摩擦角，K0为静止土体侧向压力系数，f为管-土摩擦系数。相关参数取值见表1，Xu为土弹簧屈服位移。

表1 土弹簧相关参数取值

1.2 人工地震动合成

以北京市典型Ⅱ类场地作为分析案例，为探究不同设防烈度下土体参数不确定性对埋地管道接口张开量的影响，并尽量消除地震动不确定性的干扰，采用Ⅱ类场地设计反应谱作为目标加速度反应谱，分别考虑重现期为100 a(0.1g)、475 a(0.2g)以及2 450 a(0.4g)3个抗震设防水准[23]。通过三角函数叠加法合成3条不同设防烈度的人工地震动[24]，如图4所示。人工合成的地震动为地表地震动，由于埋地球墨铸铁供水管道埋深较浅，距离地表较近，该合成地震动可直接用于模型输入。考虑地震动沿管道传播的行波效应模拟地震动的非一致激励，根据《室外给排水和燃气热力工程抗震设计规范》[23]场地剪切波速取为300 m/s。

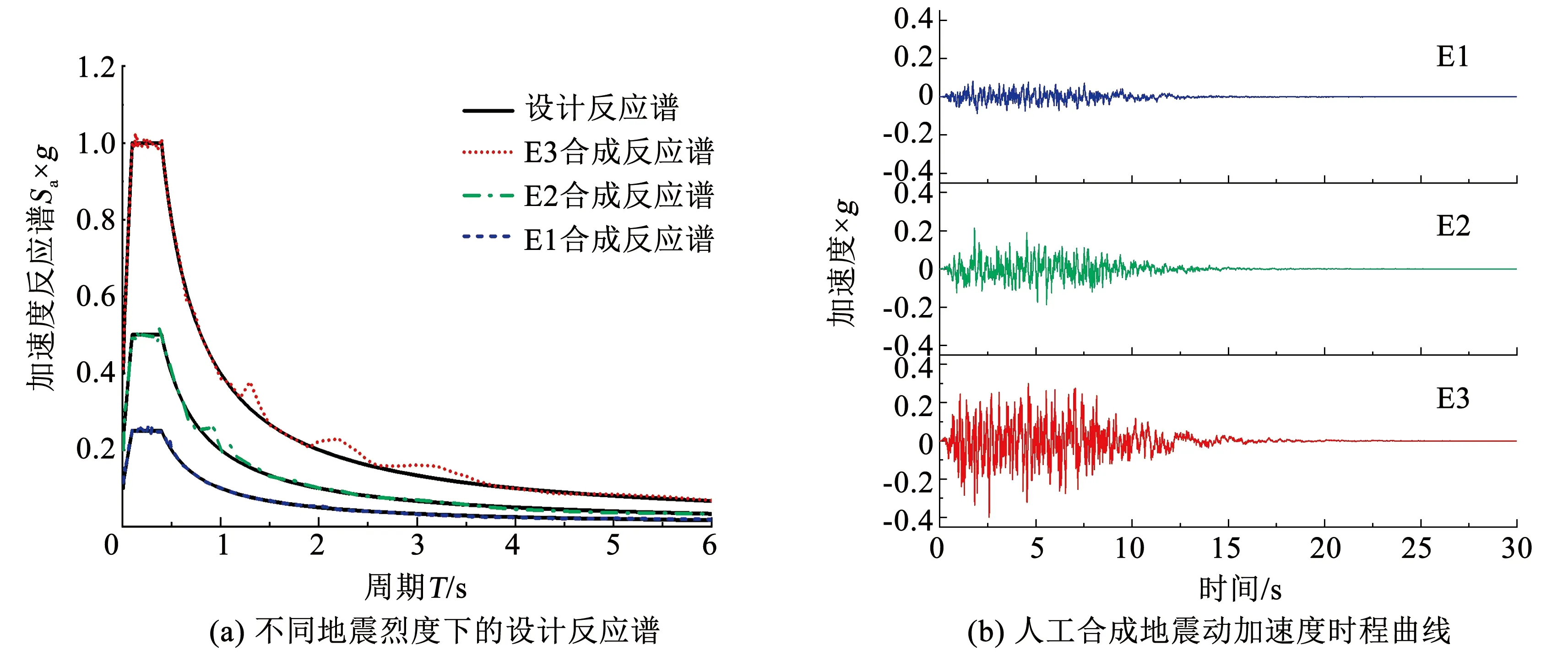
图4 不同抗震设防烈度下设计反应谱及对应的人工合成地震动加速度时程曲线

1.3 薄弱接口模型

在地震动作用下，球墨铸铁供水管道接口处会产生一定的张开量，接口张开量达到一定程度会发生轻微渗水甚至严重漏水，进而导致管道功能失效。基于已有承插式接口试验研究统计[16,25-28]，承插式球墨铸铁管道接口允许张开量约为53 mm。但管道在实际安装过程中接口处的安装深度存在一些误差，以及管道接口处管材和止水胶圈的老化腐蚀，导致管线局部出现接口力学性能弱化，在地震作用下更易发生破坏。假设管道模型中间(第50个接口)存在一个薄弱接口，在此设定薄弱接口抗拉强度折减系数α=Fw/FJ，该接口处的极限抗拉强度为Fw={0.2,0.4,0.6,0.8}×FJ[29-30]，薄弱接口示意如图5所示。

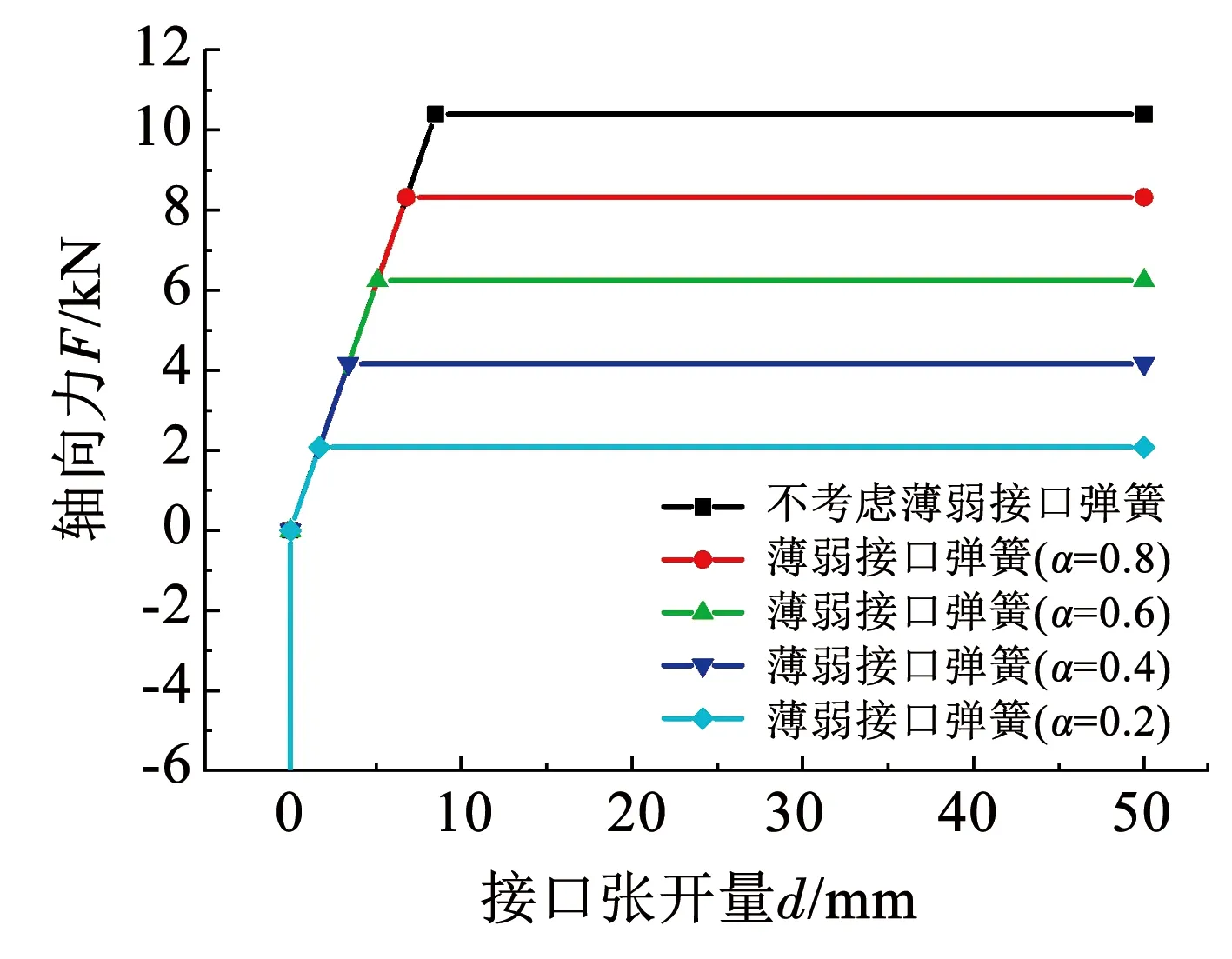
图5 薄弱接口示意

图6为不同条件下薄弱接口张开量对比，由图6(a)可以看出，薄弱接口处的张开量发生突变，这是因为单个接口强度相对周围其他接口较小时发生变形集中；相同地震动强度条件下，随着薄弱接口比值的增大，接口张开量逐渐减小。相同接口强度条件下，随着地震动强度的增大，薄弱接口最大张开量增大，如图6(b)所示。

图6 不同条件下薄弱接口最大张开量

2 土体参数不确定性及计算工况

2.1 土体关键参数的不确定性

在管道-土体相互作用分析中，土体参数的不确定性主要体现在土弹簧关键参数的不确定性。由式(1)、(2)可知，影响土弹簧计算且与土体有关的参数主要包括土体重度、内摩擦角、黏聚力、土弹簧屈服位移这4个参数。为提高后期工作的计算效率，拟对以上4个参数进行敏感性分析，剔除对分析结果影响较小的参数，再开展后面的工作。

基于龙卷风图进行参数敏感性分析，该方法可以清晰直观地确定对结构响应敏感性较高的不确定参数，是一种简单有效的灵敏度分析手段。选择管道接口最大张开量d作为表征埋地管道地震响应指标。在进行参数敏感性分析时，采用{16%,84%}分位值分别作为土体参数的上下限值，在进行非线性管-土相互作用动力时程分析过程中每次仅改变一个土体参数，其他参数取平均值，并提取管道接口最大张开量的上下限值dmin和dmax；同时，将所有土体参数都取平均值时计算得到的管道接口最大张开量d0作为基准值；计算所有参数对应条带的长度L=dmax-dmin，根据条带长度从长到短进行排列，即可得到龙卷风图。图7为罕遇地震烈度下最大接口张开量龙卷风图，其中，薄弱接口抗拉强度折减系数α=0.2和0.8。由图7可知，与其他土体参数相比，土弹簧屈服位移的不确定性对管道接口最大张开量的影响最小。因此，后文研究仅围绕重度、内摩擦角、黏聚力这3个参数展开，相关参数的均值、变异系数、抽样方法以及分布形式如表2所示。

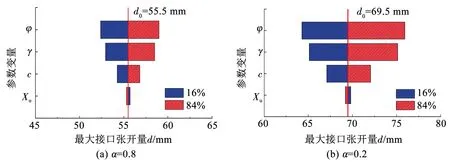
图7 罕遇地震烈度下接口峰值张开量龙卷风图

表2 不确定性参数

2.2 计算工况及分析流程

工程实际中的管道由于安装不规范、腐蚀等原因，接口强度衰减程度有所差异，本文考虑了α={0.2,0.4,0.6,0.8}共4种接口抗拉强度。针对土体参数不确定性对埋地球墨铸铁管道地震响应的影响，综合考虑5个工况的参数设置如表3所示，具体分析流程如图8所示。各工况进行500次蒙特卡洛抽样计算，分别计算3种不同设防烈度下的管道结构地震响应。涉及4种薄弱接口抗拉强度折减系数、5种工况、3种抗震设防烈度，模型数达24 012。

表3 不确定算例工况参数设置

3 模型计算及结果分析

3.1 收敛性分析

蒙特卡洛方法需多次计算同一个模型，输出同一个参数结果，并建立输出结果的统计分布规律[34-35]。然而，抽样次数过少会导致结果不收敛，无法解决问题，抽样次数过多则易导致计算量过大，严重影响分析效率。基于表2中的均值、变异系数及抽样方法对土体重度、内摩擦角、黏聚力3个随机变量参数分别进行抽样20、40、…、500次，并按照图8的分析流程进行埋地球墨铸铁管道地震响应分析，并将不同抽样次数下管道接口最大张开量均值、标准差与抽样500次最大接口张开量均值、标准差进行归一化处理，如图9所示。可以看出，随着抽样次数的增加，归一化值逐渐趋于1，模型逐步趋于收敛。在抽样150次左右时，E1、E2地震烈度下归一化均值趋于1，然而在E3地震烈度下达到收敛时的抽样次数约为300；相对归一化均值来说，归一化标准差波动范围较大，3种地震烈度下的模型均在抽样450次时达到收敛。因此，综合考虑计算精度和效率，采用蒙特卡洛抽样，抽样次数为500。

图8 考虑土体参数不确定性的球墨铸铁供水管道抗震分析流程

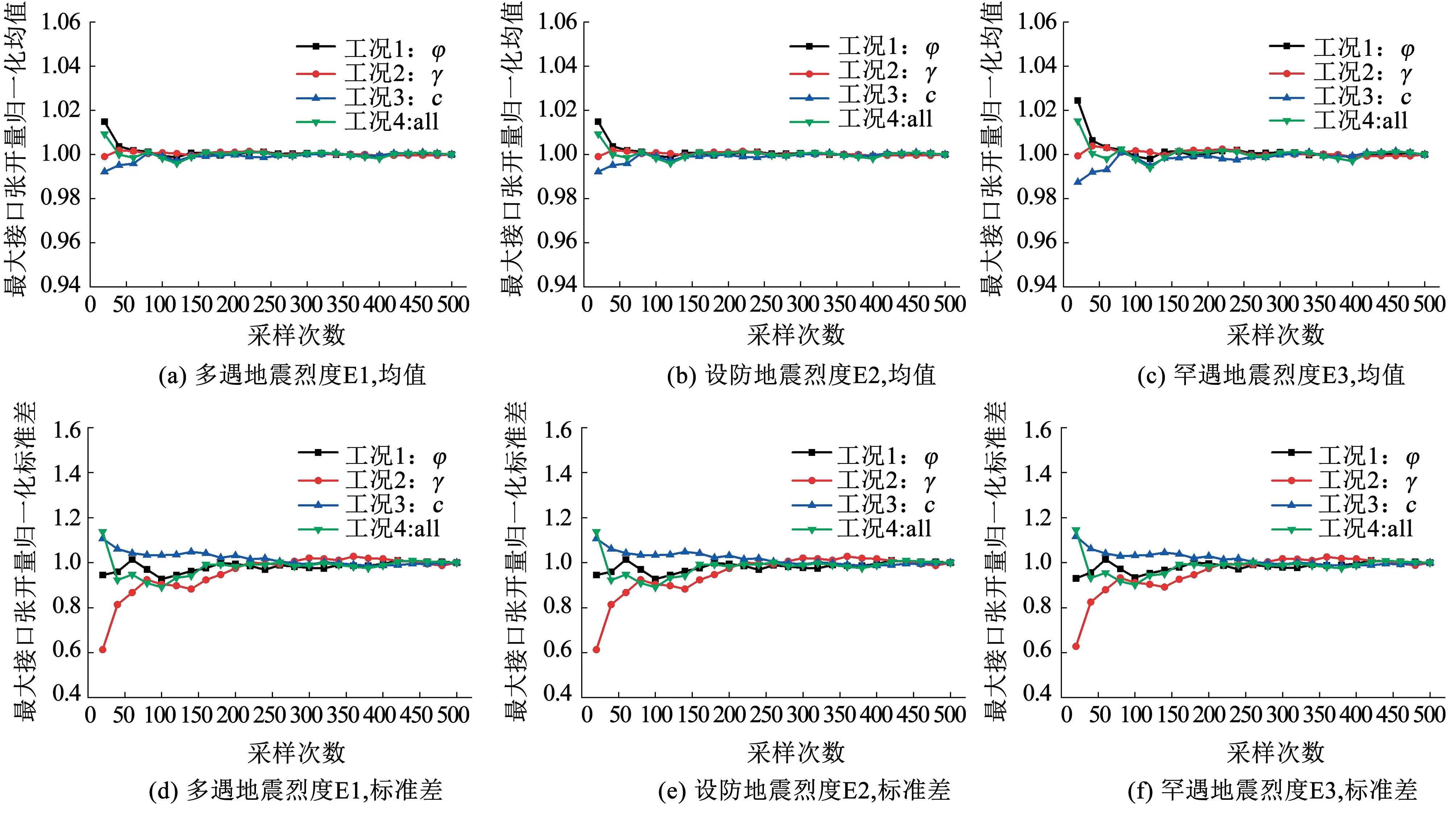
图9 不同抗震设防烈度下最大接口张开量的归一化均值和标准差(α=0.2)

3.2 薄弱接口峰值张开量变化规律

图10统计了不同抗震设防烈度下薄弱接口峰值张开量分析结果。图中虚线对应工况5的计算结果，柱状图高度对应该工况所有计算结果的均值，误差棒区间表示计算结果的标准差(可反映计算结果的离散程度)，图中的每一个小圆点代表一次计算结果，从其分布范围可看出其离散程度以及接口张开量最不利值，离散度越大则说明该参数对于接口张开量的影响越大。图11给出了各工况最大接口张开量的变异系数，可以看出，相同α时，随着抗震设防烈度的增加，变异系数逐渐增大。以设计的最不利工况为例，即α=0.2且考虑全部参数不确定性，从E1到E3管道最大接口张开量变异系数从5.90%变化至9.54%，增加了61.7%。相同抗震设防烈度时，随着α的增加，最大接口张开量变异系数逐步减小。同样以本文设计的最不利工况为例，即罕遇地震烈度E3且考虑全部参数不确定性，当α从0.8减小到0.2时，变异系数从7.56%增加至9.54%，增加了26.2%。同时，从图11可以看出，变异系数从大到小的顺序为工况4、工况3、工况1、工况2。在同一抗震设防烈度、同一薄弱接口系数下，3个参数不确定性同时考虑时对接口张开量的影响最大，仅考虑黏聚力工况次之，接着是仅考虑内摩擦角工况，仅考虑重度工况影响最小。

图10 不同抗震设防烈度下薄弱接口峰值张开量分析结果

图11 管道接口最大张开量变异系数

为量化随着地震动强度的增加不确定性工况下接口张开量最不利值dm以及均值da的变化规律，以薄弱接口抗拉强度折减系数α=0.2为例，表4列出3种不同烈度、4个不确定性工况下计算结果的最不利值dm、均值da与工况5(不考虑参数不确定性)结果d5的比值，即βn=dmn/d5和λn=dan/d5(其中，n表示工况编号)。可以看出，随着地震动强度的增加，βn逐渐增大，考虑土体参数不确定性对应的接口张开量最不利值是工况5结果的1.09～1.31倍，λn基本不变，这说明随着抽样次数的增加，计算结果的均值趋于不考虑参数不确定性工况。同理，为量化随着薄弱接口系数的减小，不确定性工况下接口张开量最不利值dm以及均值da的变化规律，以罕遇地震烈度工况为例，表5给出了不同薄弱接口系数土体参数不确定性影响放大倍数。可以看出，随着薄弱接口系数的减小，βn逐渐增大，考虑土体参数不确定性对应的接口张开量最不利值是工况5结果的1.11～1.31倍，λn同样基本不变。综上，不确定性分析中，土体参数随机变量对接口张开量最不利值影响较大，对接口张开量均值影响很小。因此，在管道抗震性能分析和设计时，需要考虑土体不确定性引起的管道响应的变异性和不利工况。

表4 不同抗震设防烈度下土体参数不确定性影响放大倍数

表5 不同薄弱接口抗拉强度折减系数下土体参数不确定性影响放大倍数

薄弱接口抗拉强度折减系数α对于接口最大张开量的影响至关重要。从图10可以看出，随着α的减小，接口最大张开量呈线性增长，根据数值模拟结果可拟合一条预测曲线。分别对同一α所有工况的结果求均值，如图12所示，根据已有的计算数据拟合出不同抗震设防烈度下关于薄弱接口抗拉强度折减系数α与接口张开量d的关系预测公式，该公式可用于在区间0<α<1时管道接口张开量的预测。但该公式是由本文研究结果拟合而成，存在一定局限性(即仅针对特定地震动强度、薄弱接口数量为一且位置固定工况适用)。

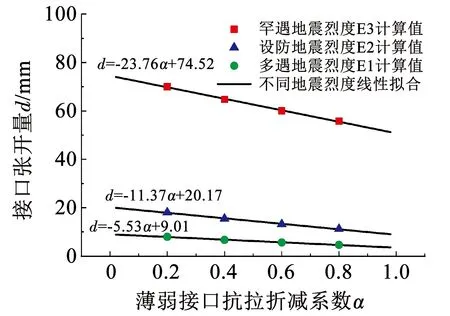
图12 不同抗震设防烈度下接口张开量与薄弱接口抗拉强度折减系数关系式拟合

4 结论与讨论

1)考虑全部参数不确定性对于管道接口最大张开量影响最大，考虑单参数对管道接口最大张开量影响程度从大到小依次为黏聚力、内摩擦角、土体重度、土弹簧屈服位移。

2)相同薄弱接口抗拉强度折减系数时，随着抗震设防烈度的增加，变异系数逐渐增大，最不利工况时(α=0.2且考虑全部参数的不确定性)变异系数从E1到E3增长了62.7%；相同抗震设防烈度时，随着薄弱接口系数的增加，接口最大张开量变异系数逐渐减小，最不利工况时(罕遇地震烈度E3且考虑全部参数的不确定性)，变异系数从α=0.8减小到α=0.2增加了26.2%。

3)不同地震动强度作用下，通过蒙特卡洛抽样模拟管道接口张开量响应，考虑土体参数不确定性的工况最不利值是确定性土参数工况相应结果的1.09～1.31倍；土参数不确定性工况的模拟均值与确定性土参数工况结果差异较小。因此，在管道抗震可靠性分析和设计时，需要考虑土体不确定性引起的管道响应的变异性和不利工况。

4)工程中由于安装不规范、管道锈蚀等原因，容易产生薄弱管道接口，本文给出了不同地震动强度下，不同薄弱接口抗拉强度折减系数与接口最大张开量的拟合公式，用于预测特定地震动强度下某一抗拉强度折减系数对应的接口最大张开量。

本研究证明了土体参数的不确定性对于埋地球墨铸铁供水管道最大接口张开量的影响较大，但需要注意的是，本研究暂未考虑各个参数之间的空间相关性；同时，拟合的公式具有一定局限性，薄弱接口程度、薄弱接口数量、薄弱接口在整条管线的位置、地震动的其他非一致性(相干效应、衰减效应、局部场地效应等)等耦合因素下的公式拟合未详细研究，后期需进一步完善。