考虑应力路径影响的垃圾土应力-应变特性

李修磊，施建勇，李玉萍

(1.山区公路水运交通地质减灾重庆市高校重点实验室(重庆交通大学)，重庆 400074；2.河海大学 岩土工程科学研究所，南京 210098)

生活垃圾作为填埋场的主体部分，其力学特性与填埋场的整体稳定密切相关[1-5]。垃圾土属于典型的各向异性复合材料，主要为纤维材料(如塑料、纺织物及皮革等)和类土材料(除纤维之外的其他材料)。由于降解作用，随填埋时间单位体积垃圾土中类土材料所占的比例会逐渐减小[6]。一些学者[7-14]已对影响垃圾土力学特性的相关因素开展了研究，如成分组成、密度、含水量、降解程度、围压以及加载速率等。Karimpour-Fard等[7-9]的三轴试验和直剪试验结果均表明，垃圾土的剪切强度特性随着密度、纤维质量分数、围压、加载速率以及超固结比的增加均有不同程度的增大；陈云敏等[10-12]的试验结果表明，垃圾土的整体剪切强度随填埋时间或降解程度的增加而增大，而黏聚力和内摩擦角分别有减小和增大的趋势；Pulat等[13-14]的直剪试验结果表明，垃圾土的剪切强度随着垃圾土中可降解有机质质量分数的增加而减小；张振营等[15]开展了垃圾土的三轴不固结不排水、固结不排水和固结排水试验，得到了不同条件下垃圾土的强度取值范围。综上，针对垃圾土力学特性的研究主要采用直剪试验、单剪试验和三轴试验，直(单)剪试验所得垃圾土的应力-应变关系近似双曲线变化，水平位移较大时逐渐趋近于水平[9-11,16-17]；不同尺寸三轴试验所得垃圾土应力-应变关系具有相同的曲线形状，均表现为持续硬化特征，应变水平较大时曲线有明显上翘，应变超过30%后仍未达到峰值或极限破坏[7-8,15,18-20]。Karimpour-Fard等[7,18]的三轴试验结果表明，无纤维质量分数垃圾土样的应力-应变曲线形状与直剪结果类似，纤维质量分数越高曲线上翘越显著。文献[9,21]将直剪试验与三轴试验结果的差异归因于垃圾填埋或试样制备过程中纤维材料近似水平趋向，与直剪试验的剪切面近似平行，导致纤维材料的加筋作用得不到充分发挥。

综上，有关垃圾土应力-应变特性影响因素的研究成果已较为丰富。填埋过程中，垃圾土可能会有多种应力状态，压缩应力、拉伸应力、加载以及卸载的情况均有可能出现，而常规三轴试验和直剪试验很难完全反映不同应力状态下垃圾土的应力-应变特性。文献[8]指出应力路径也是影响垃圾土力学特性的主要因素之一，而目前鲜有关于垃圾土应力路径的研究成果。因此，本文将对垃圾土重塑样开展不同应力路径下的三轴试验，以便更深入地认知垃圾土力学特性。

1 试 验

1.1 垃圾土试样制备

试验采用现场垃圾土制备的重塑样，垃圾样取自江苏盐城市郊外一生活垃圾填埋场，将现场钻孔取得的垃圾土样装入密封性良好的塑料桶内运至实验室；然后，将原始垃圾中尺寸较大的物体去除，如塑料瓶、大块的纺织物、木头、砖头、石块、玻璃等；再将剩余的垃圾放置在60 ℃的烘箱中至恒质量；最后，测到垃圾土的含水率为54.8%，分拣得到垃圾土中各成分所占干质量分数(见表1)。其中，泥状物主要是有机质成分(占52.3%)，包括未完全降解的食物垃圾及其他无法识别的成分。

表1 垃圾土的成分组成

根据CJJ/T 204—2013《生活垃圾土土工试验技术规程》，按照表1采用人工方式制备三轴试验所需要的垃圾土重塑样(见图1)。由于三轴仪型号尺寸的限制，所制备重塑垃圾土试样的直径为40 cm、高度为86 cm，最大颗粒粒径不超过10 mm，较长的纤维材料需剪成短纤维，其长度控制在试样直径的1/3以内。确保垃圾土重塑试样具有相同的初始状态，干密度为0.69 g/cm3，孔隙比为2.0。

图1 人工制备的垃圾土试样

试验仪器采用GDS应力路径三轴仪，对制备的垃圾土样开展不同应力路径下的三轴试验，该仪器提供了包括试样饱和、固结、应力路径、高级加载以及标准加载试验等多个试验模块，可通过需要设置控制参数，自动完成不同试验内容。试验之前，通过设定围压和轴压的变化关系即可实现不同应力路径的三轴试验。

三轴试验过程中，可以直接测得垃圾土样受到的轴向应力σ1、侧向应力σ3、轴向应变εa和体应变εv。则对应的平均正应力p、偏应力q、应力比η、径向应变εr和剪应变εs分别表示为

p=(σ1+2σ3)/3,q=σ1-σ3,η=q/p

(1)

(2)

1.2 试验方案

试验之前，采用真空抽气饱和、水头饱和及反压饱和3种方式对垃圾土试样进行充分饱和，具体步骤如下：首先将制备好的试样放入真空缸内，真空压力接近一个负的大气压并维持1 h后，打开吸水阀门使无气水真空缸内水位至淹没试样，维持8 h后打开真空缸空气阀门，使空气缓慢进入真空压力缸内；然后，将试样从真空压力缸内取出放入三轴压力室内并进行水头饱和，进水管与出水管高度差保持1.0 m，当进水量和出水量相等时水头饱和完成；再次，对试样进行反压饱和，先是对垃圾土试样施加10 kPa的围压，打开孔压阀门，记录孔压稳定后的读数，关闭孔压阀门，然后分级施加反压并同时分级施加围压，每级增量为20 kPa，同样记录孔压稳定后的读数，经过两级施加后，当围压引起的孔压增量与围压增量之比大于0.95时，认为试样饱和完成；最后，对完成饱和的垃圾土样进行排水固结，每分钟的排水量小于试样体积的0.05%时认为试样固结完成，方可开展排水条件下的不同应力路径三轴试验。

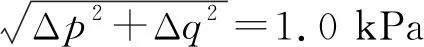
垃圾土试样在100 kPa的围压下固结完成后，共设计9条应力路径开展排水三轴试验，反映在p-q应力空间上，如图2所示。这9条应力路径可划分为压缩应力路径(包括IC0、IC45、IC72、IC90、IC108和IC124)和伸长应力路径(包括IC252、IC270和IC304)。其中，IC72和IC252、IC90和IC270以及IC124和IC304之间的夹角在p-q应力空间上均为180°。以IC45路径为例，IC表示等压固结，“45”表示应力路径与p轴正方向的夹角，用θ表示。其他信息见表2。

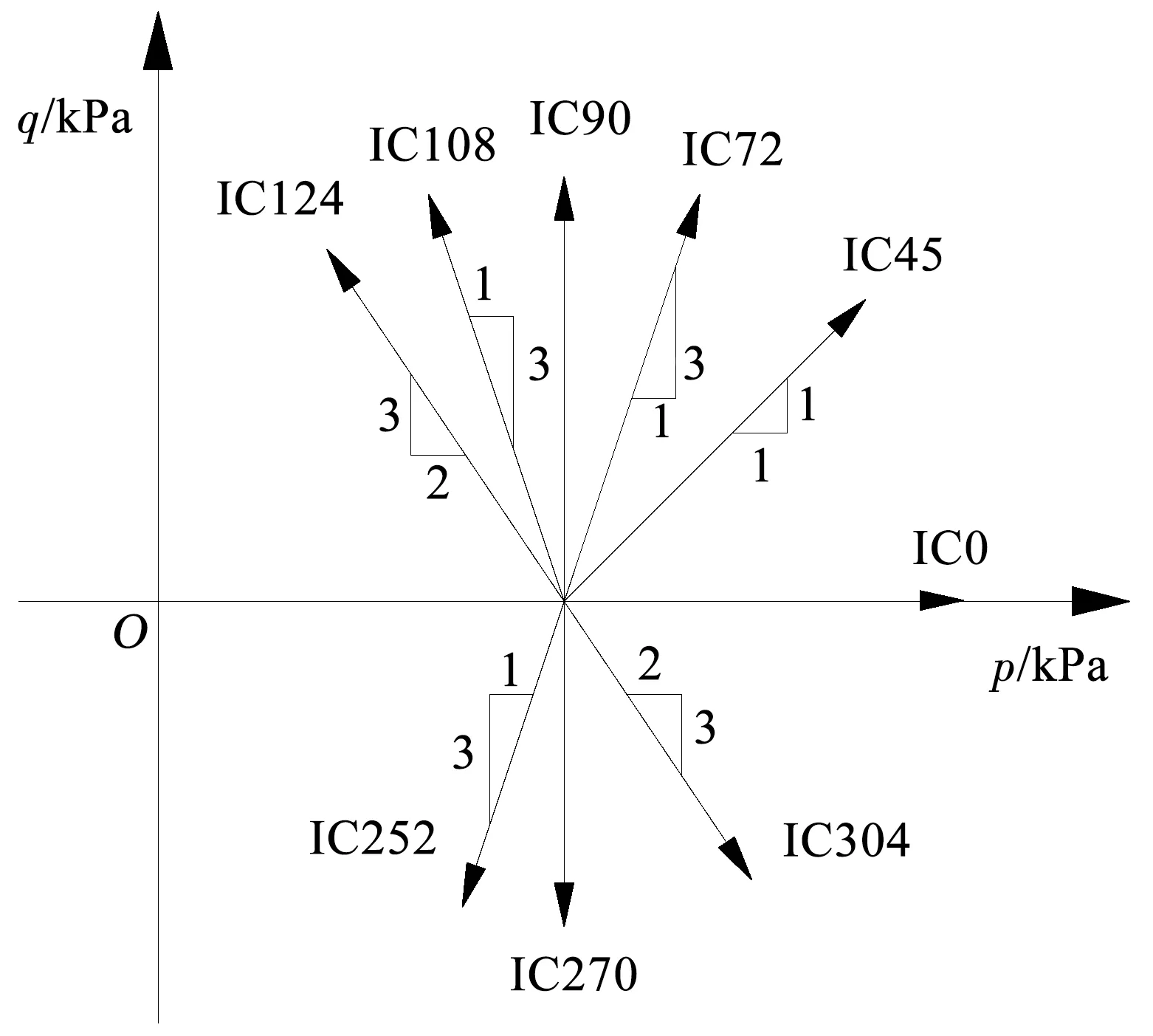
图2 三轴应力路径试验方案

根据表2可以将图1中的9条应力路径划分为3大类：围压增量Δσ3≥0的压缩应力路径，包括IC0、IC45和IC72路径；围压增量Δσ3<0的压缩应力路径，包括IC90、IC108和IC124路径；偏应力增量Δq<0的伸长应力路径，包括IC252、IC270和IC304。

表2 三轴应力路径试验说明

2 垃圾土的应力-应变关系

2.1 围压增量Δσ3≥0的压缩应力路径

在IC0、IC45和IC72 3种路径试验中，当平均正应力增量为Δp时，偏应力增量Δq分别为0、Δp和3Δp。图3给出了3种Δσ3≥0的压缩路径IC0、IC45和IC72试验所得垃圾土的应力-应变关系曲线。由于IC0路径中偏应力q=0，图3(a)和(c)分别给出了相应的p-εa和εv-εa关系曲线。由图3(a)可以看出，IC0、IC45和IC72路径试验所得的p-εa关系曲线均类似于开口向上的抛物线形状，p相同时，IC0、IC45和IC72路径对应的轴向应变依次增大(即平均正应力增量Δp相同的情况下，偏应力增量Δq越大，对应的压缩变形越大)，说明IC45和IC72路径试验中偏应力q的增加会促进垃圾土的轴向压缩变形。

图3(b)给出了IC45和IC72路径试验所得垃圾土的q-εa关系曲线。可以看出，IC45和IC72两种路径下垃圾土的q-εa关系曲线在初始段近似线性增加，轴向应变εa较大时曲线明显上翘，没有出现峰值或趋于渐近值的迹象，表现出明显的应变硬化特征；相比IC72路径，IC45路径下垃圾土的q-εa曲线出现上翘较早，且翘曲更显著。由图3(b)还可看出，轴向应变εa<20%时，IC45路径试验所得q-εa曲线位于IC72试验所得结果的下方，而随着εa的增加，IC45试验所得q-εa曲线又逐渐变化到位于IC72试验结果的上方。主要有以下两个方面的原因：其一，垃圾土为高压缩性材料，在初始加载阶段，IC45试验中较大的p使得垃圾土中孔隙减小的速度相对较快，因而相同轴向应变IC45试验比IC72试验所需的q更小；其二，应变水平增加到一定程度后，IC45试验中围压增量Δσ3>0(IC72试验中Δσ3=0)使得垃圾土的压缩变形更大，所以，纤维材料与其他颗粒成分之间的接触更紧密，形成较强的摩擦力和机械咬合力，纤维材料也就能够更好地发挥加筋效果，显著提高垃圾土的剪切强度，导致后期相同轴向应变IC45试验比IC72试验所需的q更大。

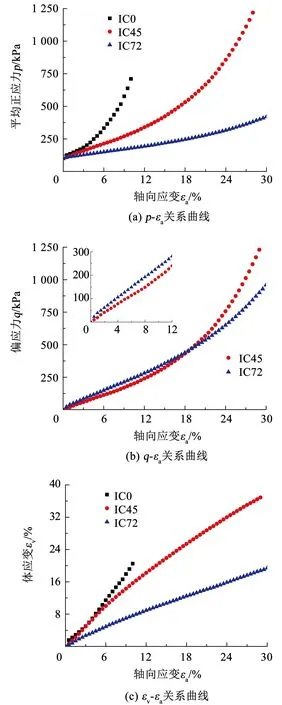
图3 Δσ3≥0的压缩路径下垃圾土的应力-应变关系

图3(c)给出了IC0、IC45和IC72 3种路径试验下垃圾土的εv-εa关系曲线。可以看出，随着轴向应变εa的增加，垃圾土的体应变εv持续增加；εa相同的情况下，IC0、IC45和IC72路径试验对应的体应变εv依次减小，说明IC0和IC45中围压的增加加剧了垃圾土的压缩变形。

2.2 围压增量Δσ3<0的压缩应力路径

在IC90、IC108和IC124 3种应力路径试验过程中，当围压减小Δσ3时对应的轴向应力σ1分别增加2Δσ3、0.5Δσ3和0，其中IC90为等p压缩路径。图4给出了3种Δσ3<0压缩路径IC90、IC108和IC124试验所得垃圾土的应力-应变关系。由图4(a)可以看出，上述3种路径试验所得垃圾土的偏应力在初始段快速增加，随着轴向应变εa的增加增幅逐渐减小，最后趋于渐近值，垃圾土的q-εa关系并没有出现上翘曲线形状，而是类似双曲线变化。

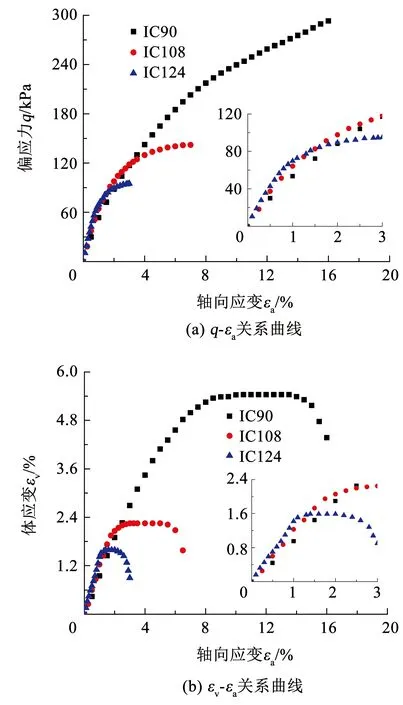
图4 Δσ3<0的压缩路径下垃圾土的应力-应变关系

由图4(b)可知，虽然IC90、IC108和IC124属于平均正应力增量Δp≤0，但这3种路径下垃圾土的体应变仍然为正值，说明试验过程中偏应力q的增加对体积变化有重要影响；垃圾土的体应变εv在初始段随εa增加而增大，εa增大到一定时，εv几乎不变保持为定值，明显不同于IC45和IC72路径的试验结果。对比图4(b)和图3(c)可知，εa相同时，IC90、IC108和IC124的体应变远小于Δσ3≥0的IC45和IC72压缩路径，说明IC90、IC108和IC124试验中围压的减小会使垃圾土样受到的侧向约束逐渐减弱以及压缩变形量减小，进而导致垃圾土中的纤维材料与其他材料难以形成较强的机械咬合力，纤维材料也就难以充分发挥相应的加筋效果。

2.3 伸长应力路径

在IC252、IC270和IC304 3种应力路径试验过程中，当偏应力减小|Δq|时，对应的平均正应力增量Δp分别为-|Δq|/3、0和2|Δq|/3，对应的轴向应力增量 Δσ1分别为-|Δq|、-2|Δq|/3和0，其中，IC270为等p伸长路径。图5给出了3种拉伸路径下垃圾土的应力-应变关系曲线。

由图5(a)可以看出，垃圾土偏应力的绝对值|q|随着轴向应变绝对值|εa|的增加而增大，且增加的幅度逐渐减缓，其|q|-|εa|关系同样类似双曲线形状；εa相等时，IC252、IC270和IC304试验对应的|q|依次增加，这是因为偏应力q相等的情况下轴向应力σ1减小的幅度依次减小，也说明了垃圾土样的伸长量取决于σ1减小的幅度。

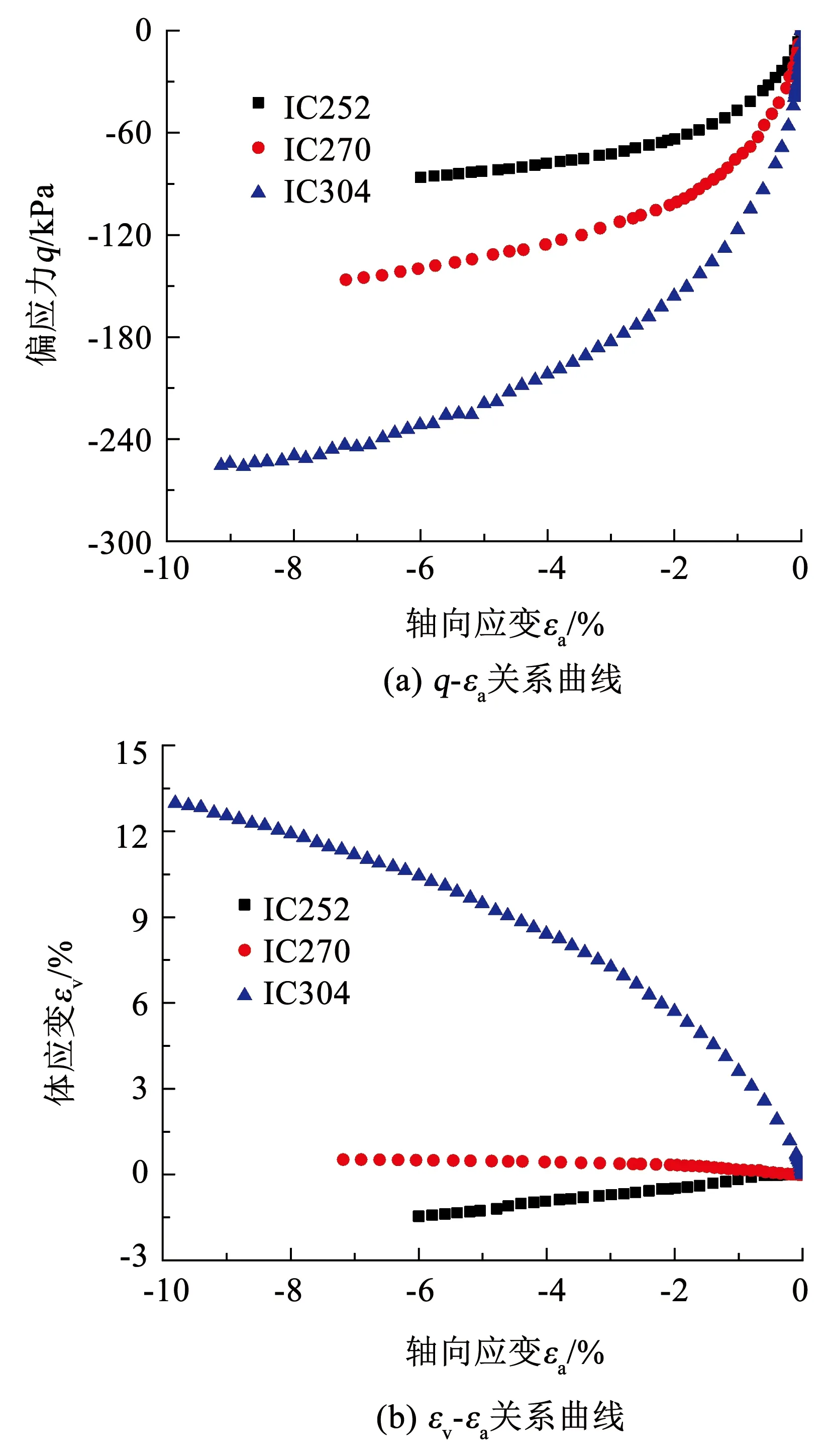
图5 伸长路径下垃圾土的应力-应变关系

由图5(b)可知，IC252路径试验所得垃圾土的体应变εv为负值是平均正应力p的持续减小所致；IC270试验的体应变非常小，接近为0，原因在于该路径试验过程中p保持不变；而IC304试验的体应变随着轴向应变εa的减小呈逐渐增大趋势，原因在于该路径试验中p是持续增加的，而p与垃圾土的体积变化密切相关。

3 垃圾土与砂土应力-应变关系比较

据相关文献[22-23]报道，砂土与垃圾土具有相近的渗透系数(10-1～10-4cm/s)，两种土体最大的差异在于垃圾土中含有大量的纤维材料，以下将对不同应力路径下垃圾土与砂土之间应力-应变特性的差异性进行分析，进而揭示垃圾土中纤维材料在不同应力路径下起到的加筋作用效果。许成顺[24]、曹培[25]和孔亮等[26]分别针对3种砂土进行了固结围压为100 kPa下三轴应力路径试验，3种砂土的相对密实度分别为60%、45%和48%。

图6 IC72和IC252路径下垃圾土和砂土的应力-应变关系

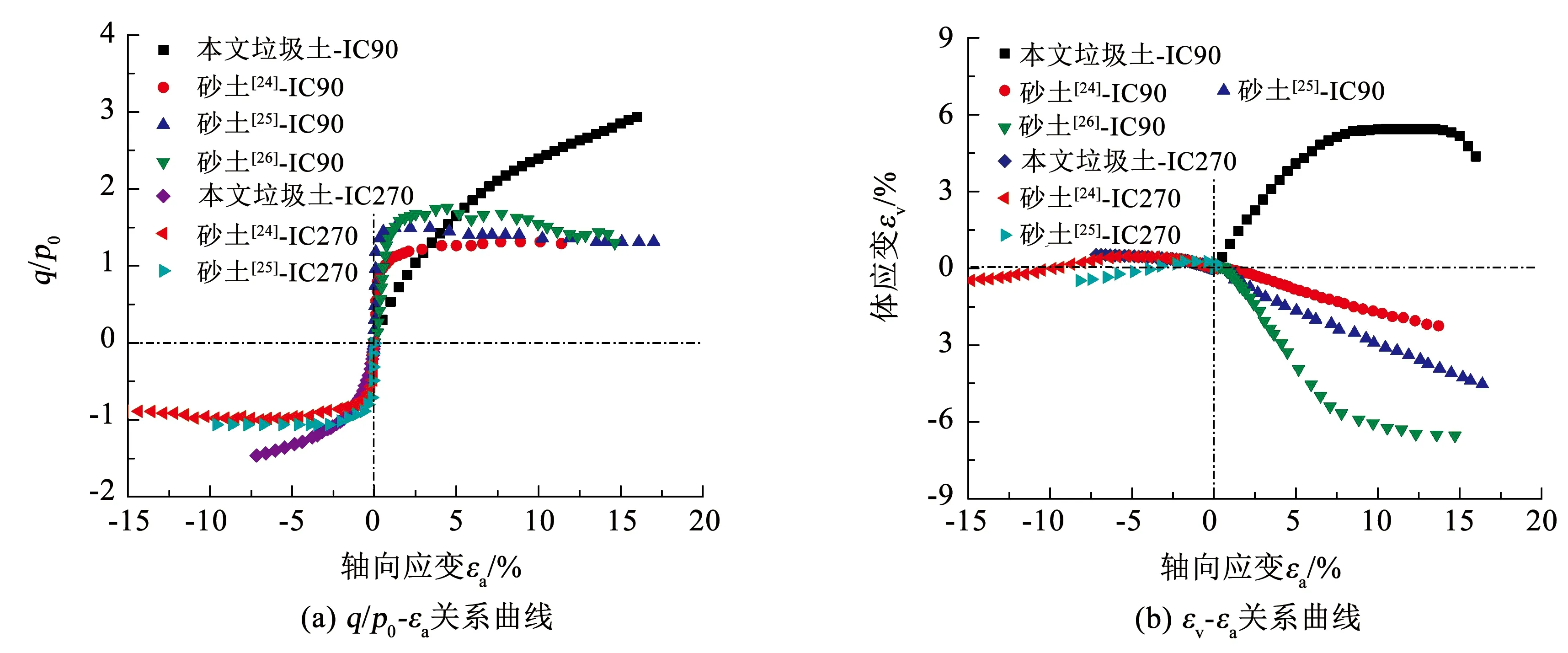
图7 IC90和IC270路径下垃圾土和砂土的应力-应变关系

图8 IC124和IC304路径下垃圾土和砂土的应力-应变关系

由图6(b)、7(b)和8(b)中IC72、IC90和IC124试验的εv-εa关系曲线可知，3种压缩路径下砂土表现出明显的应变软化和剪胀特性，而垃圾土具有显著的应变硬化和剪缩特性；伸长路径IC252和IC270试验下垃圾土和砂土的体应变εv随轴向应变εa的变化趋势基本一致。但是，对于IC304路径试验，εa相同的情况下，垃圾土的体应变εv远大于砂土，主要是围压的增加导致了垃圾土中孔隙的快速减少，与垃圾土的高压缩特性有关。

4 应力-应变关系的数学模型

不同路径试验所得垃圾土的η-εa关系曲线如图9所示。可以看出，5种压缩路径(应力比η和轴向应变εa均为正值)和3种伸长路径(η和εa均为负值)下垃圾土的应力比绝对值|η|均表现为随轴向应变绝对值|εa|增加而增大的变化趋势，且|η|增大的幅度在逐渐减小；η相同时，5种压缩应力路径(IC45、IC72、IC90、IC108和IC124)试验对应的εa依次减小。

根据图9中不同应力路径下垃圾土应力比η随轴向应变εa的变化关系，可采用双曲线模型对其进行描述，见式(3)，也可将式(3)转化为直线方程，见式(4)。其中，截距为a，斜率b对应应力比η极值的倒数。

(3)

(4)

不同应力路径下垃圾土的η-εa试验曲线与模型计算值的对比，如图9所示，相关数学模型参数见表3。由图9和表3可以看出，试验曲线与模型计算值有较高的相关性；对于5种压缩路径(IC45、IC72、IC90、IC108和IC124)，对应的模型参数a和b均呈依次减小趋势；对应的3种拉伸路径(IC252、IC270和IC304)，模型参数a依次增大，b先增大后减小。也说明采用双曲线能够很好地描述不同应力路径下垃圾土η-εa的关系。a、b与夹角θ之间的数学表达式如下：

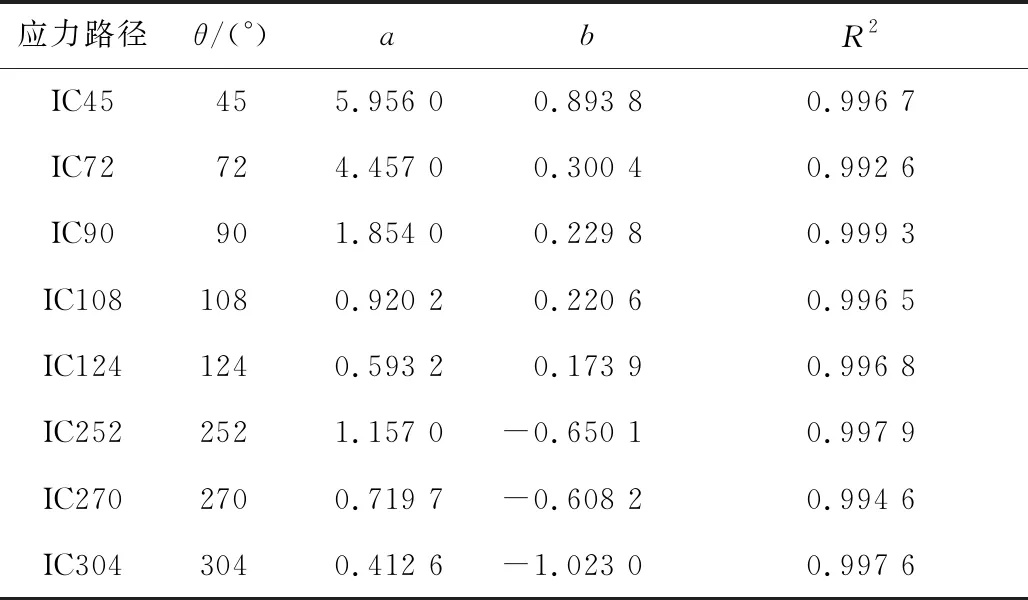
表3 不同应力路径下垃圾土的模型参数

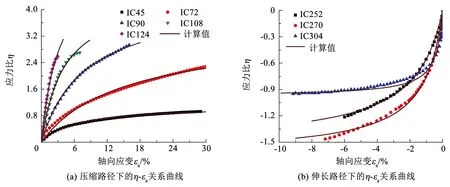
图9 不同应力路径下垃圾土的应力比与轴向应变的关系

(5)

b=θ[2.935(50|sinθ|/θ)3-3.925(50|sinθ|/θ)2+

1.743(50|sinθ|/θ)-0.24],R2=0.987

(6)

5 垃圾土的屈服特性

屈服状态的确定是在弹塑性力学框架下量化土体变形特性的一种有效方法，有关普通土体的屈服特性已有学者[27-28]进行了详细研究。“屈服”通常定义为土体应力-应变曲线偏离初始线性变化的突变点。屈服点是应力-应变曲线弯曲段屈服前后外延线夹角的平分线与试验曲线的交点。另外，利用应变能W与应力比η之间的关系也是确定屈服点常用的方法[29]。对于每一种应力路径，本文也将采用W-η的关系确定垃圾土的屈服点。为了增加可信性，还会采用q-εs、p-εv、η-εs和η-εv曲线作为辅助。将屈服点绘制于p-q应力空间上，进而得到垃圾土的屈服面形状。

总应变能W为体积应变能Wv与剪切应变能Ws之和，其积分形式为

(7)

为了方便计算，体积应变能Wv与剪切应变能Ws的增量形式为

(8)

(9)

基于上述确定屈服点的方法，得到了等压固结条件下垃圾土在p-q应力空间上的屈服面(即状态边界面)形状，如图10所示。IC0、IC45和IC72路径试验得到的应力-应变曲线表现出明显的应变硬化特征，并没有衰减发生屈服的迹象，因而这3种路径下应力-应变曲线的突变点并不是真正意义上的屈服点。其他路径对应的屈服点均与普通土体相似。由图10可以看出，垃圾土的状态边界面在p-q应力空间上类似于倾斜的椭圆，并不是关于等向压缩路径IC0(即p轴)对称，等向压缩固结线更靠近于伸长应力路径对应的屈服轨迹。以上说明，在试验过程中垃圾土样未达到屈服之前就已经产生了明显的各向异性，尤其是垃圾土样中纤维材料水平趋向的横向结构性在IC45和IC72路径试验过程中变得更加明显。

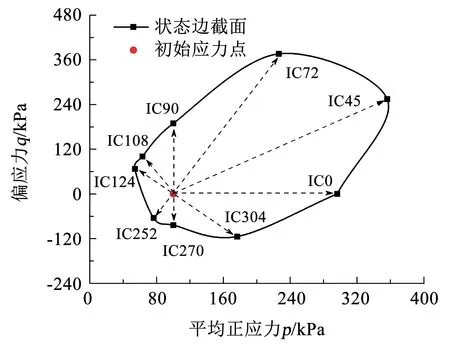
图10 垃圾土在p-q应力空间上的状态边界面

由前述垃圾土的应力-应变和屈服特性可知，垃圾土表现出明显的各向异性，不同应力路径下纤维材料在垃圾土中起到的加筋作用存在显著的差异性。因而，考虑垃圾土的各向异性以及应力路径对纤维材料所起加筋作用的影响，对于构建垃圾土的本构模型具有重要意义。

6 结 论

1)通过三轴应力路径试验研究了等压固结条件下垃圾土应力-应变特性，发现只有Δσ3≥0的压缩路径试验得到的应力-应变关系表现出增长性上翘的曲线特征，具有显著的应变硬化特征；无论是Δσ3<0的压缩路径还是Δq<0伸长路径下垃圾土的应力-应变曲线表现出类似双曲线的形状，与砂土的性质相似。通过对比砂土的应力-应变特性发现，垃圾土中的纤维材料只有在Δσ3≥0的压缩路径试验中能够起到显著的加筋作用；Δσ3<0的压缩路径下纤维材料起到的加筋作用相对很弱，且随围压减小速率的增加逐渐减弱；Δq<0的伸长路径下纤维材料很难起到加筋作用。压缩路径下，垃圾土表现为明显的剪缩性，而砂土的剪胀性比较突出。

2)通过分析不同应力路径下垃圾土应力比随轴向应变的变化规律，给出了统一描述垃圾土应力-应变关系的数学模型。

3)等压固结条件下垃圾土状态边界面的形状类似于倾斜的椭圆，并不关于等压固结线p轴对称，而是更靠近于伸长路径，可归因于不同路径下纤维材料所起加筋作用差异性所致。构建垃圾土的本构模型时，需同时考虑垃圾土的各向异性以及应力路径对纤维加筋作用的影响。