单轴菲涅尔反射聚光CPV/T系统的分析与研究

谢 飞

(上海电力大学 能源与机械工程学院, 上海 201306)

实现2030年碳达峰、2060年碳中和的“双碳”目标,减少化石能源的使用,建立绿色环保的可再生能源体系迫在眉睫。在这一时代背景下,太阳能作为一种持续稳定的可再生能源,最终将会替代传统能源,成为社会发展的动力源[1]。太阳能发电、集热是目前对于太阳能利用的主要形式,相同能量的电能和热能,因为品质因数的不同,其价值也不同[2]。电能传输和存储方便,转化成其他形式能量时转换效率高,因此在太阳能综合利用过程中,光伏发电是首选,集热作为补充。合理匹配电能和热能的输出,实现价值的最大化,是太阳能电-热综合利用系统研究的重要方向[3]。

聚光是提高单位面积辐照强度最有效的方法。它需要通过光学聚焦和追踪控制来实现[4]。聚光从形式上可分为点聚焦和线聚焦两类,从原理上可分为菲涅尔聚光和抛物面反射聚光两类[5]。追踪算法则通过建立日地运动模型,将太阳位置用表达式表示出来。随着考虑因素的增加,太阳位置算法的复杂程度也相应增加。从实用性的角度考虑,在满足追踪精度要求的同时,算法易于编程、减少运算量就显得非常重要[6]。

聚光在提高辐照量的同时会造成电池温度上升,影响光伏电池的转换效率。研究表明,温度每上升1 K,单晶硅、多晶硅电池的效率会降低约0.4%[7]。太阳能聚光的电-热综合利用系统CPV/T是一种互补的解决方案,不但可以提高光伏效率,而且还可以附带生产热能,提高太阳能的电-热综合利用率,在理论研究和实验中都取得了良好效果[8]。

1 菲涅尔反射聚光分析

相对于透镜聚光,菲涅尔反射聚光成本低,结构简单,对环境要求低[9]。菲涅尔反射聚光系统设计原理如图1所示。

图1 菲涅尔反射聚光原理

图1中:H为高度;R为每块反射镜到原点的距离;α为反射镜与x轴的夹角;β为反射光与x轴的夹角;φ为反射光与y轴的夹角;i1为入射角;i2为反射角;D为聚光接收器宽度;W为反射镜宽度。通过多组反射面将太阳光汇聚到光伏组件接收器上,反射聚光的光路几何关系为

(1)

确定了H和R后,就可以确定每块反射镜的倾角α为

(2)

聚光接收器宽度D=160 mm,高度H=1 955 mm,反射面两边对称布置,然后根据R就可以计算出反光板夹角α。菲涅尔反射聚光片的位置参数如表1所示。

表1 菲涅尔反射聚光片的位置参数

2 主动追踪算法

2.1 太阳位置算法

对太阳位置的追踪分为两类:一类通过传感器被动检测辐照量追踪太阳位置,适用于对精度要求不高的非聚光系统;另一类则通过建立精确的数学模型,根据经纬度和时间推导出太阳的具体位置[10]。

2.2 太阳的黄道经度

地球公转的平面为黄道平面,地球自转的平面为赤道平面[11]。以地球为中心建立一个天球体,如图2所示。

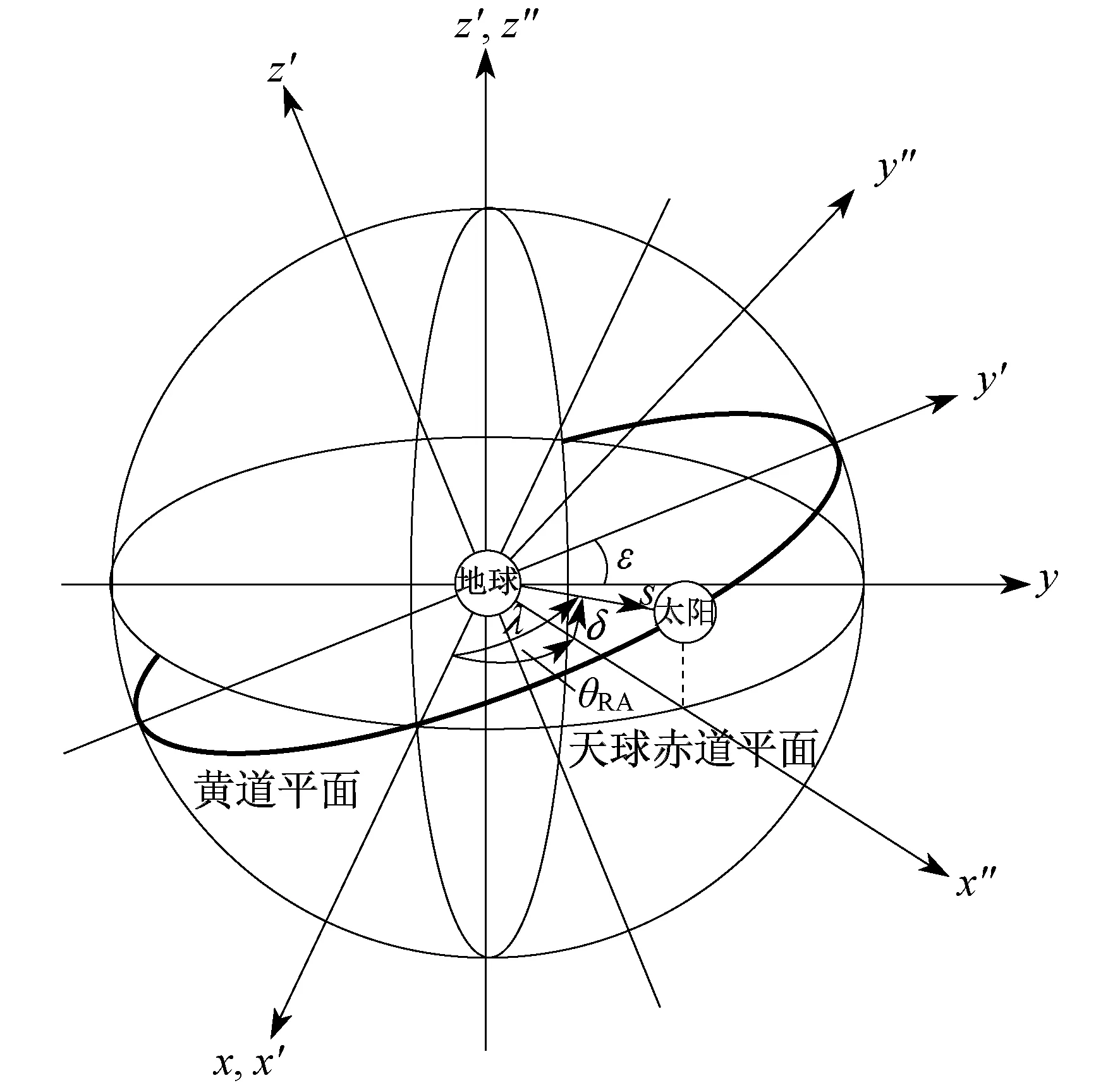
图2 赤道平面坐标系构成的天球体

以地心为坐标系原点,建立黄道空间坐标系(x′,y′,z′)和赤道空间坐标系(x,y,z)。其中:黄道平面和赤道平面相较于x(x′)轴,两平面夹角ε≈23.45°。在黄道空间坐标系(x′,y′,z′)中,日地运动变成太阳绕地球逆时针旋转。当太阳位于x′轴上时,就是一年中的冬至(或夏至)。太阳方向S与赤道平面的夹角为赤纬δ,黄道经度λ是由地心指向太阳的方向向量S与x′轴的夹角。θRA为赤道经度,用来描述太阳所转过的角度。

λ的表达式为

( 0° ≤λ<360° )

(3)

式中:n——一年中的第几天。

2.3 太阳的赤纬

在赤道空间坐标系(x,y,z)中,δ的表达式为

sinδ=sinλsinε

(4)

2.4 时 角

时角ω为地球每天自转过的角度。当本地时间正午时ω=0°,表达式为

ω=15°(TL-12)

(5)

式中:TL——以小时计时的本地时间。

2.5 太阳的高度角

以观测者为原点,建立地平面坐标系(S,E,P),其中P轴垂直于地平面,E轴为东方,S轴为南方,太阳在地平面坐标系中的位置如图3所示。

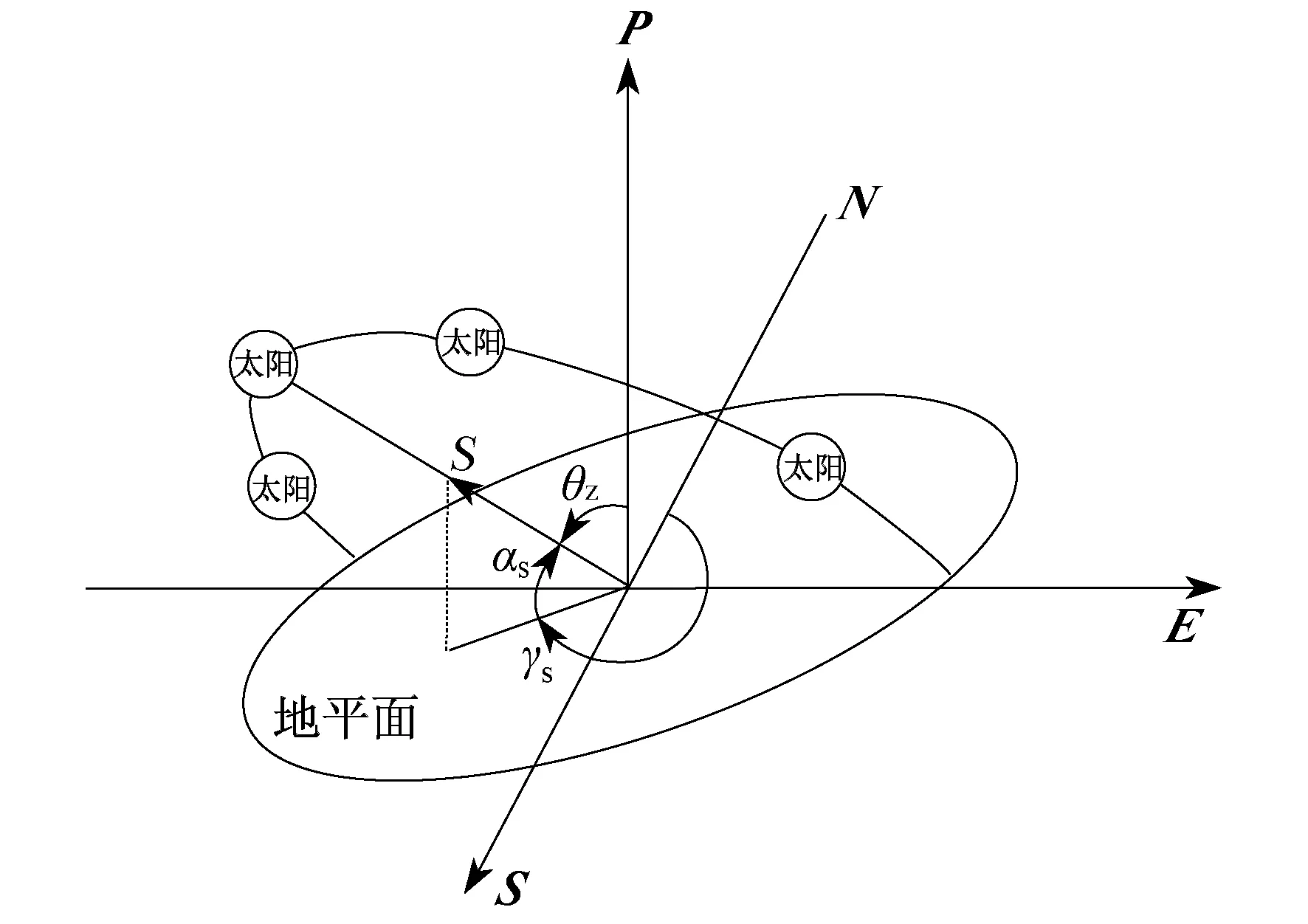
图3 太阳在地平面坐标系中的位置

图3中:αS为S与地平面的夹角;γS为S在地平面上的投影与正北N的夹角;Qz为太阳方向法平面与水平面的夹角。αS的表达式为

αS=sin-1(cosδcosφcosω+

sinδsinφ)

(6)

式中:φ——观测点的纬度。

2.6 太阳的方位角

在地平面坐标系(S,E,P)中,γS的表达式为

(7)

2.7 儒略日计时

儒略日(Julian Day,JD)中的小数部分表示当天的时间JD(t)。tyy为年,tmm为月,tdd为日,th为格林尼治时(北京时间th-8),tm为分钟,ts为秒。儒略日划分天是从正午12点开始的。2000年1月1日12点的儒略日数JDN为2 451 545。为了简化计算,将2000年1月1日作为计算的起始时间。根据太阳位置算法,给出的儒略日JD的表达式[12]为

JDN=

(8)

(9)

JD(t)=JD-JDN

(10)

2.8 考虑赤经影响修正

地球绕太阳转动的过程中,不考虑公转的因素,通常认为一天为24 h,地球自转一圈360°。但如果考虑绕太阳的公转,地球表面观测点太阳到达相同的高度角,地球实际转动的角度就超过了360°。这就是赤经对太阳位置的影响[13],如图4所示,每天要多转(θRA2-θRA1)的角度。

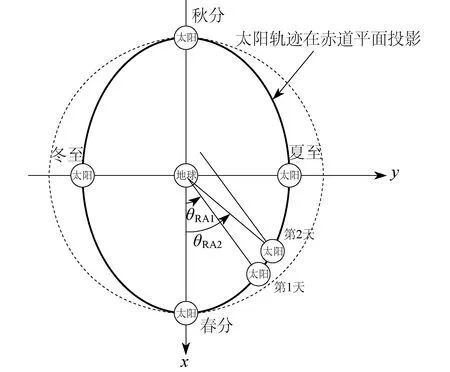
图4 赤经对太阳位置的影响

地球表面任意位置的时角ω关于儒略日时间JD(t)的表达式为

(11)

式中:LLOCAL——经度。

时角ω的取值范围为[0,2π]。将时角ω和纬度φ代入式(6)和式(7)就可以得到本地太阳高度角αS和方位角γS的表达式,分别为

αS=sin-1(cosδcosφcosω+cosδsin 2θRAcosφsinω+sinδsinφ)

(12)

(13)

由于受地球轨道的偏心率和黄赤夹角的影响,每日太阳方位角为180°时,并不是观测点本地标准时间的12点,全年前后误差约为±15 min。如果按照标准时间确定方位角,最大会产生8°的角度误差。引入赤经因素影响修正算法后,方位角每日误差小于1°,满足低倍聚光对追踪算法精度的要求。考虑赤经修正后方位角误差对比如图5所示。

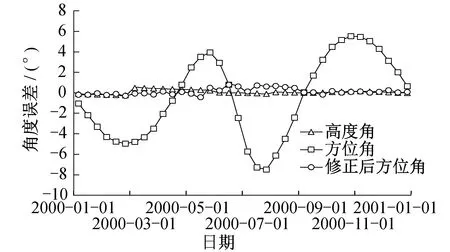
图5 考虑赤经修正后方位角误差对比

3 结果分析

使用TracePro对菲涅尔反射聚光后聚光器上的光强分布进行模拟分析,结果如图6所示。

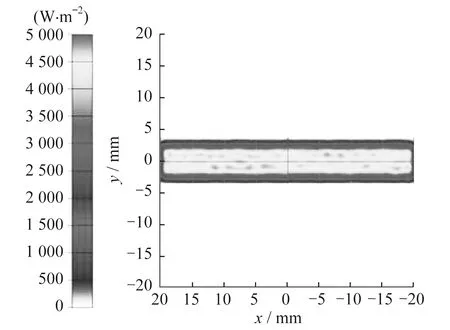
图6 菲涅尔反射聚光接收器上光强分布

由图6可知:在接收器区域光强分布均匀;辐照度最小值为4.824 6×10-16W/m2,最大值为4 806.5 W/m2,平均值为3 671.9 W/m2,均方值为1 351.3 W/m2,总光通量为0.881 25 W;入射光线为148 104条。

考虑到追踪过程存在的误差,针对出现1°～5°的追踪误差接收器能量的变化进行分析。当追踪精度误差大于3°时光学损失>30%,所以菲涅尔反射聚光系统的追踪精度应控制在±3°内,以便聚光系统总的利用率大于70%。菲涅尔反射聚光追踪误差对太阳能总利用率的影响如图7所示。

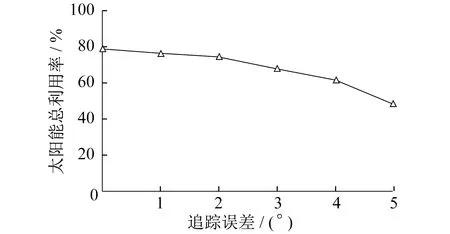
图7 菲涅尔反射聚光追踪误差对太阳能总利用率的影响

选取一日的试验数据,横坐标为时间,纵坐标左侧为功率,右侧为温度,将菲涅尔反射聚光与非聚光进行对比,实验结果如图8所示。图8中:曲线1为太阳直接辐射时光伏输出的最大功率;曲线2为10倍聚光后光伏输出的最大功率;曲线3是未聚光时接收器(即电池)的温度;曲线4是10倍聚光后接收器上的温度。

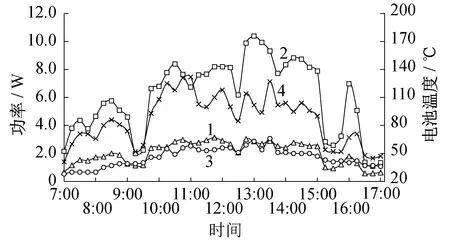
图8 菲涅尔反射聚光与非聚光对比实验结果

由图8可以看出,当天气晴朗、无云层时,聚光可以明显提高光伏电池的发电功率;当云层遮挡太阳后,聚光和非聚光发电效率相当,体现不出聚光的优势。由此表明,菲涅尔反射聚光系统在提高常规光伏电池输出功率的同时,可以获得一定的热能,可以实现太阳能电-热综合利用。

在菲涅尔反射聚光实验过程中,采用热成像仪对接收器进行拍摄测量。实验在同一日不同辐照度的情况下进行,组件温度分布情况如图9所示,最高温度点在37～132 ℃之间。

图9 不同聚光强度下接收器上的温度分布

由图9可以看出,光伏组件的温度分布均匀,没有出现局部过热的现象。

4 结 论

通过模拟分析和实验,得到如下结论。

(1) 菲涅尔反射聚光的CPV/T系统在提高光伏电池上辐照度的同时,不会产生能量集中的区域,避免了因电池板的局部高温影响光伏转换效率、损坏电池的情况。

(2) 对太阳位置的主动追踪算法进行分析推导,修正赤经因素引起的方位角算法中误差,使得追踪算法精度误差小于1°。

(3) 电池板背部的冷却系统起到冷却电池、收集热能的作用,提高了太阳能电-热综合利用的转换效率。

(4) 对10倍反射聚光与直接辐射的光伏发电系统进行对比实验可知,CPV/T系统可以有效提高电能输出,同时避免聚光后光伏电池温度升高造成的效率下降,将冷却过程中产生的热能进行回收,实现了提高太阳能综合利用率的目的。