列车阻塞效应对地铁隧道临界风速的影响
夏三县 张晓伟 胡璠 王海涛
1 郑州地铁集团有限公司
2 北京城建设计发展集团有限公司
3 河南工业大学土木工程学院
当地铁隧道发生火灾时,地铁列车通常需要停在火灾的上游位置。当车辆拥堵在火源的上游位置时,地铁列车阻塞效应会改变隧道的流速和流场分布,因此,列车堵塞会对临界风速造成影响。火灾临界风速是地铁隧道烟气控制的关键参数,隧道风速大于临界风速可以防止火灾烟气逆风流传播,可以给乘客撤离提供无烟安全撤离路线[1]。因此,研究列车阻塞效应对地铁隧道临界风速的影响具有重要意义。
2000 年开始隧道阻塞对临界风速的影响得到学者们的关注和重视[2-4],但大部分学者着重研究公路隧道阻塞比对火灾临界风速的影响,鲜有地铁隧道的相关研究[5]。Li 等[6]研究了汽车阻塞效应对公路隧道临界风速的影响。Lee 等[7]研究了火源在阻塞车辆的上下游位置对公路隧道临界风速的影响。江荷等[8]开展了排烟口对地铁隧道火灾机械排烟效果影响的FDS 数值模拟研究。Kang[9]试验研究了车辆火灾对公路隧道临界风道的影响。王君[10]开展了地铁长区间隧道火灾工况风速的实测试验和研究分析。地铁隧道与公路隧道的截面形状、截面尺寸和隧道材料均不相同,因此本文开展了地铁列车阻塞效应对地铁隧道火灾临界风速的影响,给出考虑地铁列车阻塞效应的地铁隧道火灾临界风速计算公式。
1 数值模拟和热烟验证试验
1.1 地铁隧道三维数值模型
本研究在FDS 软件中建立了水平地铁隧道三维物理模型。地铁隧道截面形状为矩形,隧道尺寸长宽高为100 m×4.8 m×5.3 m。隧道地板、墙壁和顶板为钢筋混凝土。火源尺寸长宽高为1 m×1 m×0.5 m,火源热释放速率设为5 MW。火源设置在隧道70 m 处地板中心位置,列车尺寸长宽高为40 m×2.8 m×3.8 m,列车位于隧道入口30 m 处。隧道外风速设置为0 m/s,隧道外空气温度设置为20 ℃。
1.2 单元格尺寸敏感性分析
数值模拟的单元格尺寸可以根据火源特征直径计算确定。单元格尺寸取火源特征直径的1/12~1/4 比较合适。式(1)给出了火源特征直径的计算公式。
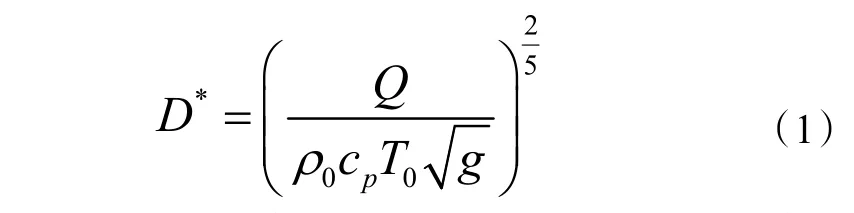
式中:D*是火源特征直径,m;Q 是火源热释放速率,kW;ρ0室外空气密度,kg/m3;cp是空气的定压比热,kJ(kg·K);g 是重力加速度,g/s2;T0是空气温度,K。
图1 给出了不同单元格尺寸的隧道内的温度分布情况。单元格尺寸小于0.3 m 时,温度的变化已经趋于稳定,因此本文采用0.2 m 单元格尺寸。
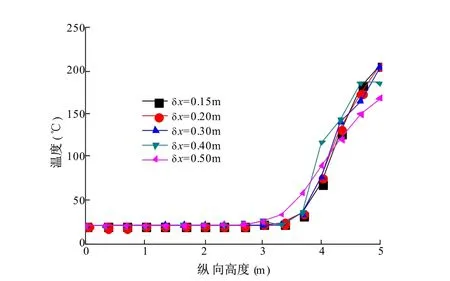
图1 火源下风侧5 m 垂直方向的温度分布图
1.3 热烟验证试验
本研究在真实地铁隧道内开展了热烟试验,用于验证FDS 模拟结果的正确性。试验时热源的热释放速率为23.03 kW。隧道内风速0.25 m/s。图2 比较热源下风侧0.5 m 处隧道断面距地面高度1 m 处空气温度预测值和实测值,两者的最大偏差小于0.8 ℃,误差率小于5%,表明FDS 模型的模拟准确性很高。

图2 数值模拟预测温度和实测温度对比
2 数值模拟结果和分析
2.1 列车阻塞长度对隧道临界风速的影响
通过改变列车的长度,研究了不同阻塞长度对火灾烟气返流长度的影响。阻塞长度是指发生火灾时地铁列车长度。火源位于隧道送风入口端70 m 处,列车位于火源上游侧且紧邻火源。隧道与大气连通的一个端口设置为“SUPPLY”,用于产生1.4 m/s 的纵向风速。隧道的另一个端口设置为“OPEN”,用于模拟室外大气环境。图3 和图4 分别给出了不同阻塞长度的火灾烟气返流长度情况和温度云图。

图3 不同阻塞长度的烟气返流长度

图4 不同阻塞长度的温度云图
由图3 和图4 可知,阻塞长度对隧道火灾临界风速影响不明显,阻塞长度10、20、30 和40 m 的火灾烟气返流长度基本相同。地铁列车的车厢较长,车厢长度均超过10 m。由此,可以认为阻塞长度对地铁出入线隧道火灾临界风速基本没有影响。
2.2 列车阻塞比对地铁隧道火灾临界风速的影响
在隧道长度100 m、火源热释放速率7.5 MW 模拟条件下,通过改变列车的高度研究了地铁列车阻塞比对地铁隧道临界风速的影响。隧道纵向风速为1.6 m/s,列车距离隧道入口30 m,地铁列车长度为40 m。图5 和图6 分别给了阻塞比10.46%、20.92%、31.38%和41.84%时地铁隧道的烟气返流长度情况和温度场云图。

图5 不同阻塞比的烟气返流长度
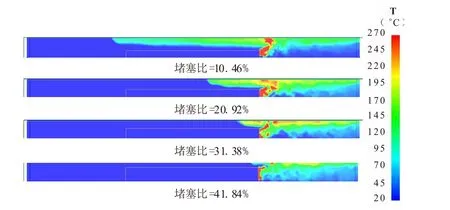
图6 不同阻塞比的温度云图
由图5 和图6 可知,阻塞比对地铁隧道火灾烟气返流长度影响较大,阻塞比10.46%的火灾烟气返流长度最长,阻塞比41.84%的火灾烟气返流长度最短。随着隧道阻塞比逐渐增大,火灾烟气返流长度逐渐变短。究其原因是列车会使隧道截面积变小,进而会增加隧道内的纵向风速,使隧道烟气返流长度和临界风速变小。隧道阻塞区域和隧道无阻塞区域的隧道风速之间存在以下关系时:

式中:ρ1和ρ2是分别是阻塞区和非阻塞区域的空气密度;Ab是隧道阻塞区域的隧道截面积;A 是隧道非阻塞区域的隧道截面积;φ 是隧道的阻塞比。
3 地铁隧道火灾临界风速模型修正
现有研究表明隧道火灾临界风速与火灾热释放速率、空气密度、隧道外部环境空气温度、空气比热、重力加速度和隧道几何尺寸密切相关。隧道临界风速可以表示为以上几个影响因素的函数。
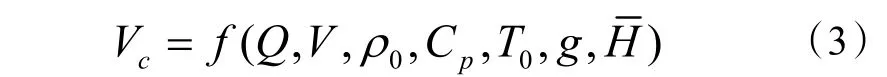
通过无量纲分析,式(3)可以用以下公式表示:

式中:H 是隧道水力直径;Vc是隧道临界风速;V*是无量纲隧道风速;Q*是无量纲火源热释放速率。
式(4)的系数需要根据隧道具体情况确定,Tang等人[11]开展了公路隧道火灾临界风速的热烟试验,并根据试验数据给出了公路隧道的临界风速预测模型。
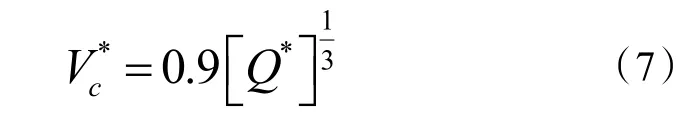
本文采用直接观测法确定数值模拟研究的地铁隧道火灾临界风速。直接观测法通过改变地铁隧道送风风速,直至肉眼观察烟气恰好不发送隧道火灾烟气返流现象,此时的隧道风速即为地铁隧道火灾临界风速。利用经过验证的FDS 数值模型模拟研究了0%、10.46%、20.92%、31.38%和41.84%阻塞比时的地铁隧道火灾临界风速,并根据不同阻塞比时的地铁隧道临界风速的数值模拟数据,采用非线性回归方法拟合给出了考虑地铁列车阻塞时的地铁隧道临界风速预测公式:
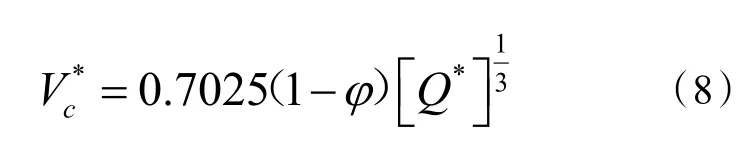
式中:φ 是地铁隧道阻塞比。
随着地铁隧道阻塞比的增加,地铁隧道火灾临界风速逐渐变小。地铁隧道阻塞比的增大率与临界风速的减小率之间呈线性关系。比较式(7)和式(8)可知,水平地铁隧道火灾临界风速小于Tang 等人[11]给出的水平公路隧道火灾临界风速。这是因为地铁隧道的几何尺寸和断面形状与Tang 模型不同,导致Tang 模型预测值大于地铁隧道火灾临界风速。
4 结论
1)列车阻塞会改变隧道内纵向风速和风压分布情况,因此地铁列车阻塞效应会影响地铁隧道火灾临界风速。地铁列车长度变化对地铁隧道临界风速的影响很小。
2)随着地铁隧道阻塞比的增加,地铁隧道临界风速逐渐变小,反之亦然。地铁隧道阻塞比的增大率与临界风速的减小率之间呈线性关系。

