基于概率神经网络−小波神经网络−DS信息融合的电厂引风机故障诊断

张航，周传杰，张林，陈节涛，徐春梅，彭道刚

（1.国电长源汉川第一发电有限公司，湖北省 武汉市 431614；2.上海电力大学自动化工程学院，上海市 杨浦区 200090）

0 引言

随着火电机组单机容量的增大和自动化程度的提高，电厂设备的复杂度和设备间的关联性随之提高，这对设备的安全性提出了更高的要求。引风机作为火电机组关键辅机设备之一，其功能是辅助锅炉排气，将锅炉燃烧生成的高温粉尘烟气抽出，以保证炉膛的正常压力[1]。引风机的安全可靠运行关系着锅炉运行的稳定，影响着电力生产的安全性和经济性，且引风机工作环境恶劣，易发生故障，所以研究引风机的故障诊断技术有着非常重要的现实意义。

目前，对引风机的故障诊断主要有2类：一类是事后诊断，即故障发生后，现场检查确定故障类型，并查找分析故障原因[2-3]；另一类是预防式的故障诊断，是对引风机进行状态监测，对状态参数的变化特征[4-6]进行分析诊断，或是基于智能诊断方法进行诊断[6-8]。与事后诊断方式相比，预防式故障诊断可以为后续的状态检修提供有益的指导，从而可以减少非正常停机次数，延长维修间隔，提高经济效益，所以，这类故障诊断研究得到了广泛的重视。张晓斌[4]根据引风机振动信号的频域特征分析进行故障诊断，成功诊断出了引风机的故障；唐贵基等[5]研究信号的时频特征，进而诊断出了引风机的转子故障状态；周琦[6]应用引风机振动信号的时域特征作为故障的特征量，采用K-Means聚类方法进行故障诊断，提高了故障诊断的准确性。Jagtap等[8]采用了广义协调状态监测方法对引风机故障做早期监测，提高了故障诊断的准确性。但多数引风机故障诊断的研究文献是采用单一的故障诊断方法[6-8]，而单一故障诊断方法受参数和自身算法的影响可能会造成误诊现象。

鉴于引风机输送的是高温、高压、高杂质的烟气，工作环境恶劣复杂，使得传感器测得的信息具有不确定性，这些不确定性的存在，必然会给故障诊断带来一定的难度，导致故障诊断的准确率下降，同时考虑到单一故障诊断方法误诊现象。为了提高故障诊断的正确率，避免漏诊误诊的现象，需融合诊断。D-S证据理论又称Dempster-Shafer理论，是一种被广泛应用于决策级的信息融合方法[9]，其合成公式特别强调证据之间的协调性，但对冲突证据进行合成时不考虑冲突信息的影响，易得出有悖于常理的决策。因此，一些学者提出了新的合成公式[10-15]，这些公式在处理冲突证据融合时有较大的改进，融合结果也更为合理。

综上，针对引风机故障诊断，本文提出改进的D-S融合诊断方法，首先通过概率神经网络(probabilistic neural network，PNN)和小波神经网络(wavelet neural network，WNN)对故障特征信息进行初步诊断，得到基本概率分配值，再经改进的D-S融合方法进行融合，进而决策得到诊断结果，可有效提高诊断正确率，且合理分配冲突信息。

1 改进的D-S证据理论

D-S证据理论是把求某个命题概率问题看成确定该命题为真的程度问题，其不仅强调证据的客观性，也强调证据估计的主观性。证据理论发展至今，已经有50多年的历史，许多学者对其研究并取得了不少成果。

1.1 D-S融合规则

设Θ为识别框架，为一个互不相容事件的完备集合；假定幂集2Θ表示Θ的所有子集构成的集类，映射m:2Θ→[0,1]称为一个mass函数，A表示识别框架Θ的任一子集，记作A⊆Θ，且满足m(Ø)=0，且m(A)=1(Ø表示空集)，则称m为假设空间上的基本概率分配函数。基本概率分配函数反映了对A本身的置信度大小，值越大，置信度越高。m(Ø)=0反映了对空集不产生任何置信度；m(Ø)=1，A⊆Θ，表示所有命题的置信度之和应为1。

设m1、m2是Θ上的2个mass函数，A、E、F表示识别框架Θ的任一子集。D-S组合规则[9]表示为

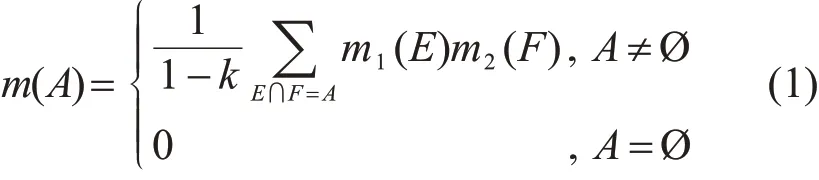
由式(1)可知，m(A)中没有体现出冲突信息的影响，冲突系数k只是作为正则化因子的一部分对其进行的归一化处理，这造成了信息的浪费，且在冲突信息较大时，容易出现与事实不符的悖论，因此需要对冲突系数进行重新合理的分配。

针对高冲突证据D-S融合可能出现与事实不符的悖论，Yager[10]认为没有真正掌握冲突信息的部分应分配给识别框架，据此提出的合成公式如式(2)所示：

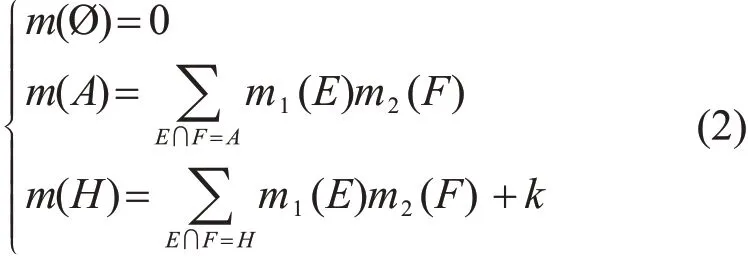
但这会导致难以获得合理的融合结果。文献[11]提出的合成公式如式(3)所示：

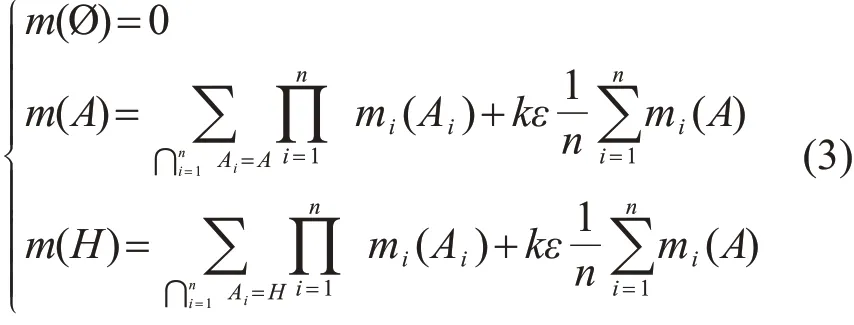
式中ε=e-k~为证据的可信度，其中k~=是n个证据中每对证据集总和的平均，反映了两两之间的冲突程度。式(3)是根据可信度和证据的平均支持度分配冲突信息的，对冲突信息有一定的利用，但仍有一部分信息被赋给了识别框架，且在证据高度冲突时，同式(2)一样，会出现未知项获取较大的支持度，导致无法做出正确的决策的情况。

文献[12]按着各个命题的置信度进行加权分配冲突信息，其合成公式如式(4)所示：

这种分配方法充分利用了冲突信息，但是没有考虑每个命题置信度的信任度。文献[13-14]在考虑证据体信任度的同时，根据焦元的信任度来分配冲突信息，可提高信任度高的焦元对结果的影响，削弱信任度低的焦元对结果的影响，融合结果比较合理。

1.2 基于改进D-S的融合规则

为了充分利用冲突信息，并对其能实现合理有效的分配，文献[13]提出基于焦元信任度改进D-S融合公式。该合成方法首先从全局的角度分析计算证据体的信任度；再从局部的角度分析焦元的信任度，进而根据焦元的信任度对冲突信息进行分配。该算法的步骤如下：

1）假设有n个证据体，其中任意2个证据体记为mi、mj，分别根据式(5)和式(6)计算证据mi、mj间的距离[15]dBPA(mi,mj)和相似度DS(mi,mj)，其表达式分别为：

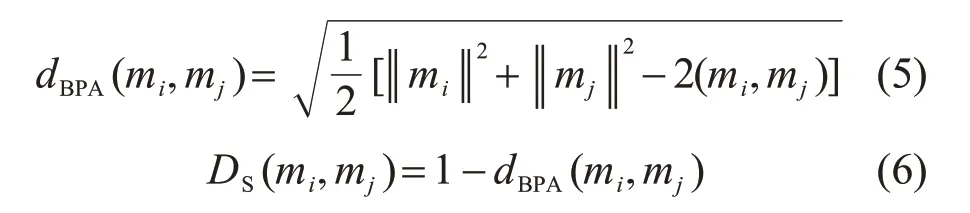
式中‖mi‖2=(mi,mi)，表示向量的内积。证据间的距离反映它们之间的支持程度，距离越小，表示证据间的支持程度越大。证据的相似度是根据证据间的距离计算的，相似度越大，表示证据间的距离越小，支持程度越大。

2）计算加权平均证据体mMVE。加权平均证据体是根据证据体的信任度对所有证据体进行加权平均得到，其计算公式如下：

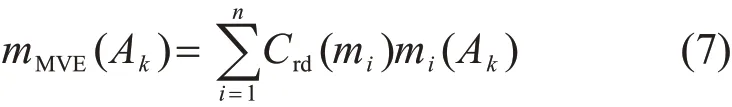
式中Crd(mi)为证据体mi的信任度，根据式(8)计算，且Crd(mi)=1。

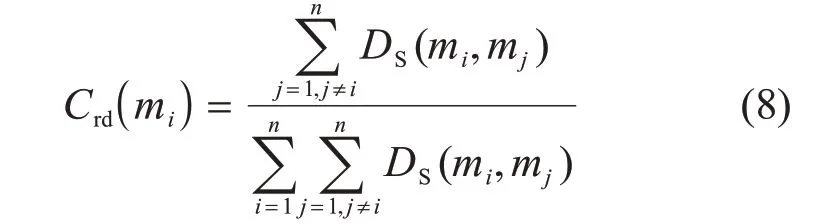
3）计算焦元的信任度FCrd[mi(Ak)]，其计算公式如下：

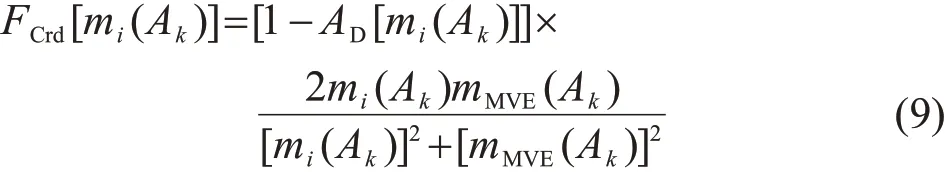
式中AD[mi(Ak)]为证据体mi和加权平均证据体mMVE同一焦元Ak的绝对距离，为AD[mi(Ak)]=|mi(Ak)-mMVE(Ak)|。

4）计算焦元的冲突分配因子Di(Ak)。焦元的冲突分配因子为焦元的信任度归一化后的值，其计算公式如下：

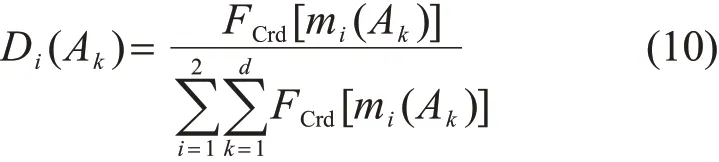
5）根据焦元的冲突分配因子进行冲突信息的分配，得到新的D-S合成公式。设m1、m2是Θ上的2个mass函数，其合成公式如下：

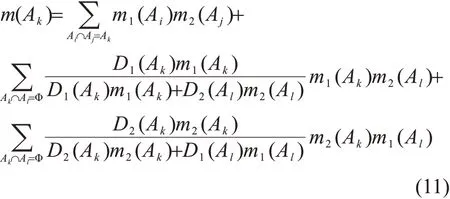
由式(11)可知，焦元的信任度Di(Ak)参与了冲突信息的分配，可提高信任度高的焦元对结果的影响，同时尽可能的降低信任度低的焦元对结果的影响。

2 基于改进D-S的融合诊断模型

2.1 基于PNN的故障诊断原理

PNN是通过Parzen窗口法计算得到概率密度估计，进而实现贝叶斯分类的一种神经网络[16]，它由输入层、模式层、类别层和决策层组成。与BP网络相比，PNN网络的优势在于不仅能用线性学习算法解决非线性学习算法所解决的问题，而且还能保持非线性学习算法的高精度等特性。PNN网络具有学习规则简单、训练速度快等优点，因此把它应用在引风机的故障诊断系统中。为了得到证据体以便于融合诊断，文中采用PNN类别层的输出作为证据体的基本概率分配值。

2.2 基于WNN的故障诊断原理

WNN是基于小波分析理论构造的一种神经元网络，它由输入层、隐含层和输出层组成。WNN的诊断策略是通过不断改变小波基的形状和尺度来调整网络的权值和阈值，进而使得误差平方和最小。WNN既有小波变换良好的局部化优势，也具有神经网络自学习能力，具有更强的逼近能力和模式识别能力，因此本文把WNN引入到引风机故障诊断系统中。

文中隐含层的神经元激励函数为Mexican Hat小波函数[17]，其计算公式如下：

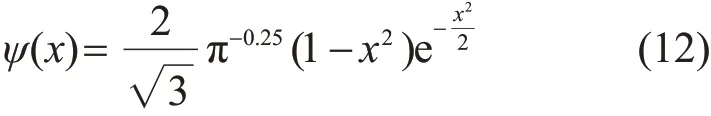
2.3 融合诊断策略

提出的基于改进D-S的融合诊断系统如图1所示。由图1可知，先把根据引风机振动信号提取的特征向量输送到PNN网络和WNN网络进行网络训练，再把测试样本输送到训练好的PNN网络和WNN网络进行初步诊断，以PNN类别层的输出和WNN的输出得到基本概率分配值，并作为证据输送到基于改进D-S的融合方法进行融合，计算出融合后的基本概率分配，经决策规则得到诊断结果。

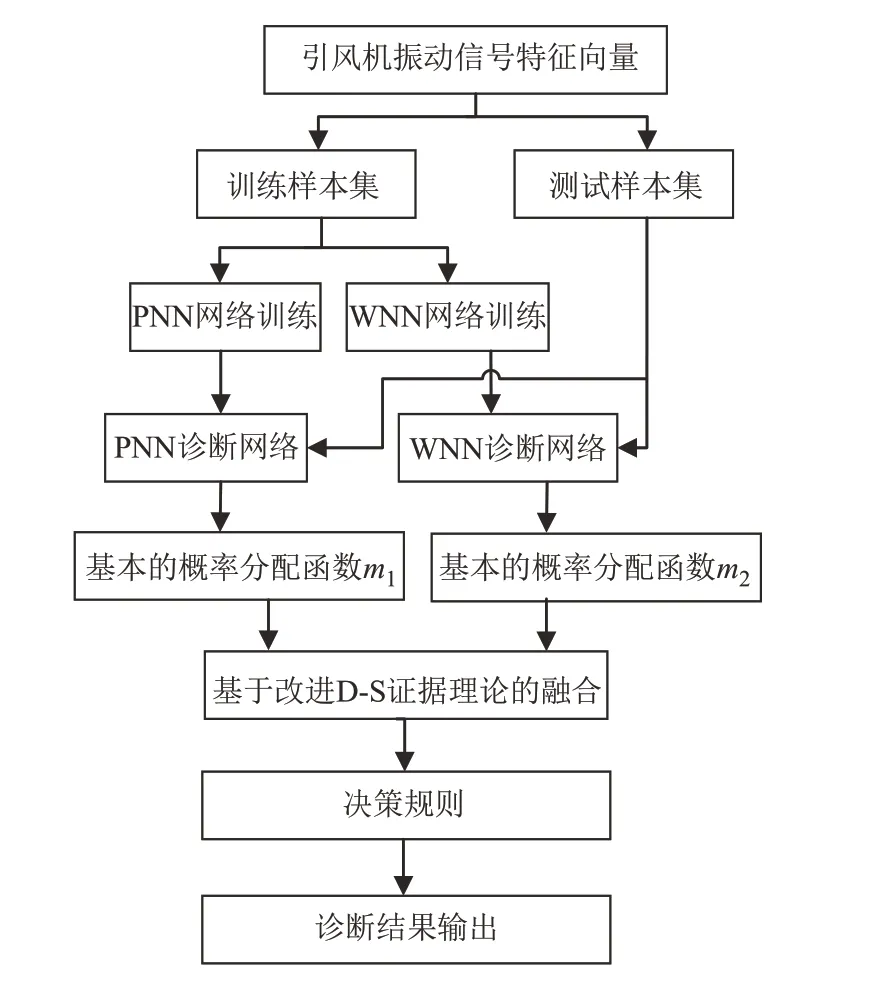
图1 基于改进D-S的融合诊断结构图Fig.1 Structure diagram of fusion diagnosis based on improved D-S

3 仿真结果及分析

3.1 引风机问题描述

引风机的状态测点，比如振动、温度、流量、压力等信息都能反映健康状态信息，其中振动信号包含的健康状态信息最为丰富，为此，根据引风机振动信号进行故障诊断。为了验证文中所提出的故障诊断方法，以某电厂3号锅炉的轴流式引风机为研究对象，选取了该引风机的轴承垂直和水平方向上振动信号，采样间隔为3 s，对引风机的转子不平衡、正常状态和裂纹故障3种状态进行诊断[6]。从引风机轴承振动号提取时域特征(平均幅值、均值、峰峰值、均方根、脉冲指标、波形指标和峰值因子)和频域特征(能量特征)组成特征向量(分别记为特征1、特征2、…、特征8)，共100个样本[6]。其中转子不平衡样本25个，正常状态样本数25个，裂纹故障测试样本50个。取90个样本为训练样本，因篇幅所限，列出部分样本，如表1所示；剩余的10个样本为测试样本，如表2所示。表1和表2中故障模式1为转子不平衡、故障模式2为正常状态、故障模式3为裂纹故障，对应目标输出分别为0 0 1、0 1 0和1 0 0。

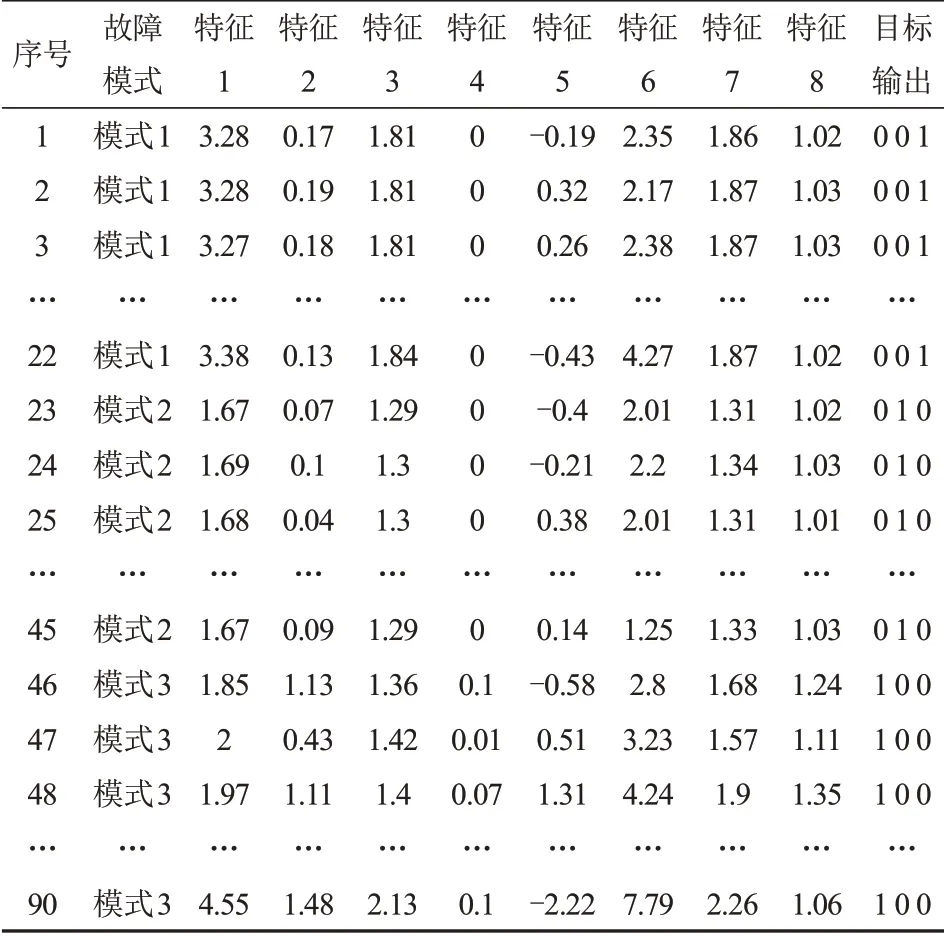
表1 训练样本数据Tab.1 Training sample data

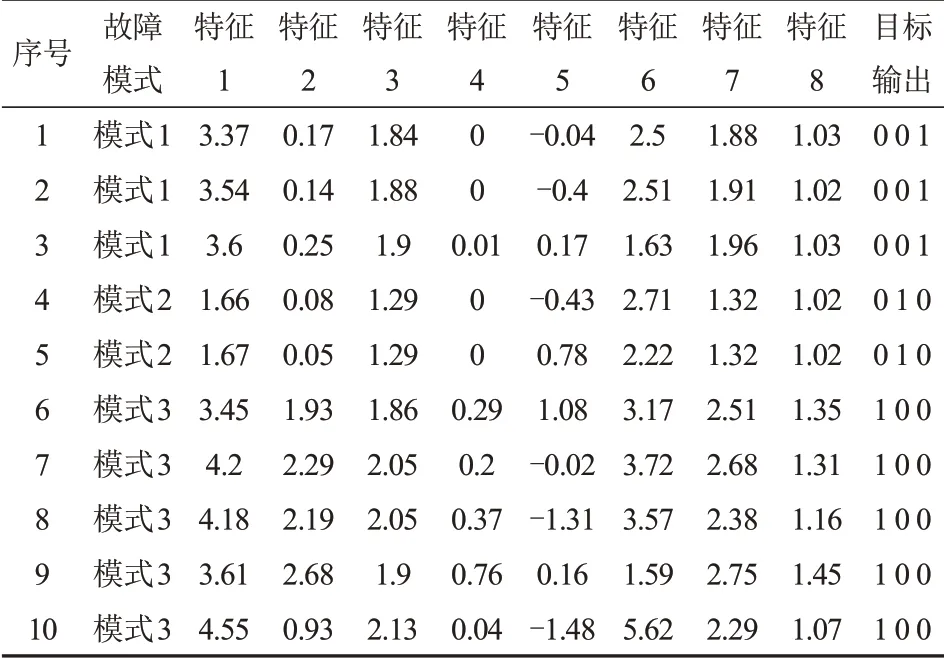
表2 测试样本数据Tab.2 Test sample data

3.2 基本概率分配

文中选取的3种故障模式：转子不平衡、正常状态和裂纹故障，分别记为A1、A2和A3，且为单一故障，即满足m(Ø)=0，且mj(Ak)=1(其中j为第j个测试故障样本向量；k表示故障类别)。

3.3 诊断结果及分析

首先把表1所示的训练样本输入到图1所示诊断网络，对PNN和WNN网络进行训练；其次，为了验证PNN和WNN的鲁棒性和泛化能力，对表2所示的样本加入5%的随机噪声得到样本和表2所示样本共50个样本作为测试样本，输入到训练好的PNN和WNN诊断网络进行诊断。

表3是PNN在不同径向基函数扩展系数spread值下的诊断正确率。由表3可知，PNN网络中径向基函数的扩展系数spread的值跟诊断结果有很大的关系，在spread=0.2时，诊断的正确率为56%，随着spread值的减小，正确率越高；在spread=0.12时，正确率达到100%；随之再减小，正确率又略微降低。结果表明在spread一定的取值范围内，故障诊断的正确率很高。

表3 不同spread值下PNN诊断的正确率Tab.3 Accuracy of PNN diagnosis under different spread values

根据样本特征向量的特点和故障模式数，取WNN网络输入层节点数为8，输出节点数为3，经训练验证隐含层节点数取10，调整输入层和输出层权值的学习率分别取值为0.5、0.5；调整小波函数的尺度因子和平移因子的学习率分别取值为0.001、0.001。在此参数设置下，不同迭代次数下的WNN诊断的正确率如表4所示。由表4可知，迭代次数由100变到150时，故障诊断的正确率从92%提高到了98%，迭代次数增加到200、300和500时，故障诊断的正确率没有变化，迭代次数继续增加到1 000和2 000时，故障诊断的正确率又有所下降。这表明WNN诊断正确率难以做到100%，所以有必要进行融合诊断。

表4 在不同迭代次数下WNN诊断的正确率Tab.4 Accuracy of WNN diagnosis under different iterations

以spread=0.12时PNN网络类别层的输出作为证据体m1，以WNN迭代300次时的输出作为证据体m2，分别用式(1)—(4)和式(11)进行融合诊断，结果如表5所示，可知除式(2)外，其他融合方法诊断结果均与实际相符。这是式(2)融合时将冲突信息幅值给了识别框架，而证据间信息又有一定的冲突，所以导致式(2)融合结果错误率高。以样本1和样本43典型融合情况为例对诊断结果进行分析，其部分诊断结果分别如表6、7所示。

表5 不同融合方法下诊断的正确率Tab.5 Diagnostic accuracy of different fusion methods

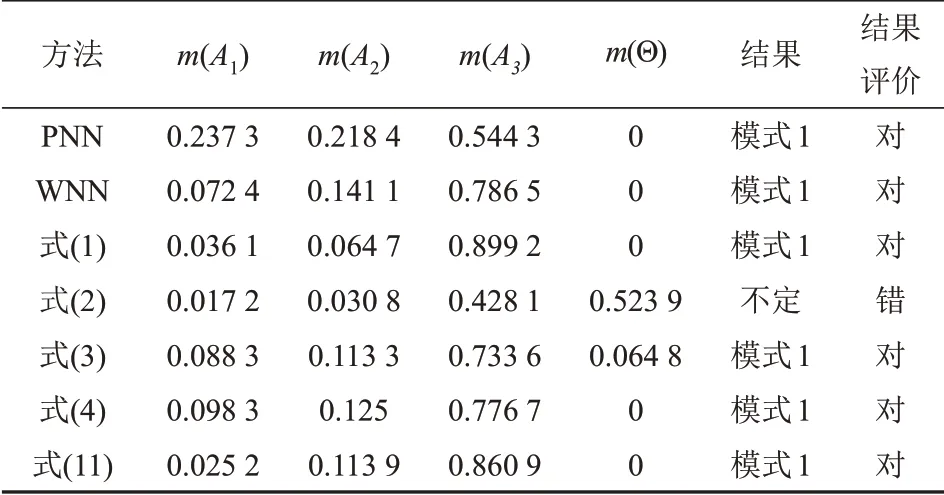
表6 测试样本1在不同方法下的诊断结果Tab.6 Diagnostic results of test sample 1 under different methods

表6是测试样本1在不同诊断方法下的诊断结果，由表6可知，样本1在PNN和WNN的初步诊断结果均为转子不平衡，支持率分别以0.544 3和0.786 5，但均未到1。由式(2)的合成结果可知，2个证据间的冲突系数为0.523 9，分别大于对3种故障的支持率，所以式(2)的诊断结果为不确定。式(1)因为正则化处理，忽略了冲突信息，所以以0.899 2的支持率支持转子不平衡，但未利用冲突信息，导致结果可靠性低。式(3)的诊断结果正确，且按着可信度的大小对冲突信息进行分配，对冲突信息有一定的利用，且减小的融合结果的不确定性，但辩识框架仍得到了0.064 8的支持率，所以未能充分利用冲突信息。式(4)的诊断结果正确，把冲突信息按着平均加权进行分配，融合后基本概率分配制介于2个证据体的基本概率分配值之间，这更像一种“折中”策略，未能使信任度更好的焦元得到更高的支持率。式(11)的合成结果为0.025 2、0.113 9、0.860 9，可知对A1和A2的支持率均低于2个证据体的支持率，对A3的支持率均高于原来证据体的支持率，这表明对信任度高的焦元提升了支持率，形成了强化作用；对信任度低的焦元降低了支持率，形成了弱化作用，这种处理更符合实际。所以利用焦元信任度可以合理地分配冲突信息，使得融合结果更为合理。

表7是测试样本43在不同诊断方法下的诊断结果，由表7可知，样本43在PNN诊断结果为转子不平衡，WNN的诊断结果为正常状态，两者诊断结果不一致，根据实际情况可知，WNN诊断结果错误。由式(2)的合成结果可知，2个证据间的冲突系数为0.655 9，因冲突系数较大，式(2)合成结果不理想，其他合成方法均与实际相符，且避免了单一诊断方法造成误诊的情况。经式(11)所述的改进D-S合成结果可知，通过焦元信任度分配冲突信息后，融合结果更为合理。

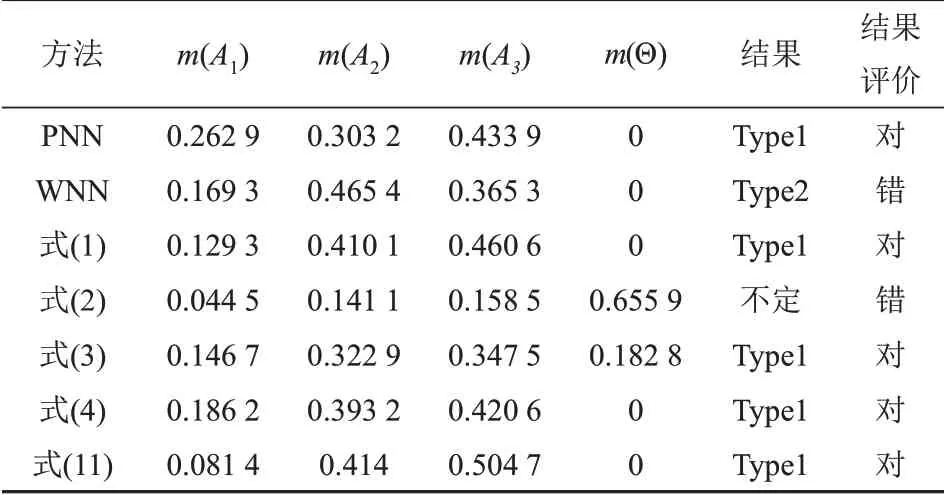
表7 测试样本43在不同方法下的诊断结果Tab.7 Diagnostic results of test sample 43 under different methods

4 结论

基于引风机故障诊断复杂性，提出了一种基于改进的D-S融合诊断方法。该方法首先通过PNN和WNN网络进行初步诊断形成证据体，再根据基于焦元信任度改进的D-S方法进行融合诊断，进而得到诊断结果。从诊断结果可知：

1）该方法成功地诊断出了所有的故障；

2）单一的故障诊断方法受参数设置或自身特点，可能会造成误诊情况；而融合诊断能避免这一情况的发生；

3）与其他合成公式相比，基于焦元信任度的改进D-S合成公式能根据证据体的信任度和焦元的信任度分配冲突信息，使得信任度高的焦元支持率得到加强，信任度低的焦元支持率得到削弱，进而诊断结果合理，可靠性高。