风电场次同步振荡等值建模方法研究

康佳乐，余浩，段瑶，陈武晖*，王丹辉

（1.太原理工大学电气与动力工程学院，山西省 太原市 030024；2.广东电网有限责任公司电网规划研究中心，广东省 广州市 510080；3.江苏大学电气信息工程学院，江苏省 镇江市 212013）

0 引言

近年来，风力发电技术发展迅速，而随着风电机组的大规模并网，随之产生的次同步振荡问题也愈发突出，严重影响风电机组和接入电力系统的安全稳定运行[1-11]。2009年10月，美国德州南部某一双馈风电场发生次同步振荡，因系统振幅过高而导致风电机组脱网及损坏[12]。2012年我国华北地区某风电场也发生了较严重的次同步振荡，造成大量风电机组脱网[13]。

风电场次同步振荡研究需要建立风电场电磁暂态模型。实际的风电场中通常包含数十乃至数百台的风电机组，风电机组之间通过电缆线路联络，电缆的长度由风机的发电特性和风机间的距离确定，各不相同。而且风电机组电磁暂态模型是高阶非线性模型，建立详细描述风电场内部每个风机和每条连接海缆或者架空线路的次同步振荡研究模型，无论从建模工作量和仿真计算时间的角度都是不可能的。因而，需要选择合适的等值建模方法，使建立的风电场次同步振荡等值模型能保留风电场与接入系统相互作用的次同步振荡特性，同时简化其建模和模型应用的复杂度。

风电场等值建模可以选用聚合法与降阶法等。聚合法是将整个风电场内的同型风电机组聚合为单台风电机组或是数量较少的几台风电机组，从而减少风电场模型复杂程度和次同步振荡计算量。文献[14]对双馈风机的建模进行了概述，并对风电系统的等值聚合进行了综述，包括风速的等值、风电场的分群、同群风机的等值方法及其对等值聚合的影响。降阶法则是采用各种方法降低风电场模型的阶数以达到简化的目的。文献[15]通过特征值分析法来考察风电场模型简化后主导状态变量的情况，利用模型降阶方法来降低风电系统的模型阶数。而风电场等值建模通常采用聚合法，当风电场进行聚合时，不仅风电机组需要聚合，风机与风机间的连接线路也需要聚合。大型风电场内集电系统的简化建模对于系统的阻抗存在一定的影响[16-19]。

风电场等值聚合方法一般分为单机等值和少量几台等值风机的风电场聚合模型。当机组间的运行差异不大，整个风电场内的风机可等值为单台机组，等值风机容量等于所有风电机组容量之和。如果不同机组间风速相差较大，等值的精度就会较差。当大型风电场内的风速分布不均匀或者风电机组型号不同时，多机等值模型优于单机等值模型。多机组等值模型在聚合时通常可以采用K-means聚类算法、层次(系统)聚类算法和最大期望EM算法等进行分群。在聚类算法确定时，可以选择单指标(风速)或多指标进行算法的优化。文献[20]对比在风速差异较大的情况下单机等值与多机等值误差，结果表明在风电场风速差异较大时，用一台风电机组难以表征风电场内所有机组的不同运行点和轴系积累能量的特性。文献[21]建立了精度较高的风速不同的多机风电场等值模型，但是当风电机组风速分散性较大时，等值风电机组的数量会增加，将导致仿真时间较长。文献[22]采用13个指标聚合，获得精度较高的多机聚合模型，但计算量较大，且所选取的13个参数不相互独立。

在选取风电机组等值聚合方法后，风机间的联络线路也需要进行等值聚合。文献[23-24]假设每台风机端电压(幅值和相位)相等的前提下提出了功率集电系统等值聚合思想，但风电场内风速，输电线路阻抗等参数不同，使得每台风电机端电流(幅值和相位)不同，因此其计算结果存在一定误差。文献[25]采用容量加权法来等值风机参数，但是该方法存在误差较大、精度较低的特点。

文献[26]提出一种基于相似度同调的双馈风电场聚合方法，通过考虑出口处发生不同故障类型时风机间功率特性的相似程度，确定相似度量化指标，并基于该指标对双馈风电场进行聚合。该方法确定相似度指标需要较大的计算量，仿真速度较慢，且该方法将整个风电场等值为单台风机，没有考虑风电场中各风机出线端电流幅值和相位不同的影响，及风机在不同风速区间内的控制策略不同的情况，忽略了风机之间的耦合性。

根据上述分析，本文计及不同风速区间的不同控制策略对次同步振荡特性的影响，采用基于风速指标K-means算法聚类风电机组，并考虑各台风电机组出线端的电流幅值和相位不同的影响，将风电机组间的集电系统进行聚合等值，提出基于功率等值的集电系统简化建模方法。所提方法不仅能将风电场等值为单台风机，还能基于风机之间的耦合性，将风电场等值为多台风机，能够较好地复现风电场次同步特性。在PSCAD/EMTDC中搭建相关风电场仿真模型，并对等值前后次同步振荡模态进行对比分析，用以验证该等值方法的合理性。

1 大型风电场等值建模原则

风电场的次同步振荡等值模型的主要建模原则如下：

1）风电场等值前后注入电力系统的功率相等；

2）风电场等值前后在公共连接点(point of common coupling，PCC)的次同步振荡幅值特性和频率特性接近；

3）风电场等值前后次同步振荡主导失稳模态的阻尼和频率随着风电场参数和系统变化规律一致；

4）在前三者的基础上，等值模型的计算仿真复杂程度能尽可能地降低。

基于上述分析，大型风电场的次同步特性动态等值，即在保持等值前后次同步振荡的振荡主要特征一致的条件下，对风机和集电系统进行简化的过程，以减少其仿真分析计算量，提高分析运行效率。本文将从风电机组的等值聚类和机组间的联络线路等值聚类加以阐述。

2 次同步振荡风电机组聚合

2.1 风电机组按运行区域分类方法思路

风电场不同位置的风机运行于不同风速，由于风机在不同风速区间内风机的控制策略不同，其对外表现出的次同步振荡特性也不同，其次同步振荡阻尼特性不能以统一的表达式表示，即不同的控制区间内的风电机组不能较好地聚合[23]。解决这一问题的方法是在不同的控制范围进行区间内的聚合。文献[27]给出了某风机风速−转速、转速−功率和风速−次同步模式阻尼曲线，如图1所示。该风机额定风速为10.5 m/s，运行风速范围为3~25 m/s，有4个运行区间或模式，即AB为低速恒转速区间，风速3~5 m/s；BC为最大风速跟踪区，风速5~8 m/s；CD为恒转速功率上升区，风速8~10.5 m/s；DE为恒转速恒功率区间，风速10.5~25 m/s。不同运行区间存在切换，对应的控制规律和参数不同，风电场次同步振荡模型等值应该计及不同控制区域内的影响。

图1 双馈风机的运行特性曲线Fig.1 Operation regions of a typical double fedinduction generator

2.2 风电机组按运行区域聚类方法

在假设风电场内的所有的机组类型相同的条件下，当风电场的风机运行工况接近时，即风速相同时，风电场单机等值模型模拟风电场次同步振荡特性具有较高精度。在风电场的风机运行风速差异较大时，风电场单机等值模型模拟风电场次同步振荡特性的精度较差，为了保证等值模型能够准确模拟实际风电场的次同步特性，将风电场中不同控制区间内的风电机聚合为多机等值模型。在运行工况差异大时，多机等值的精度高于单机等值的精度[20-21]。

本文选择的风电机组的聚合方法是基于K-means算法的风速聚类的风电场风机动态等值方法，以风速指标和风机控制策略区间对风电场的风电机组进行分组，利用风速作为不同机组间的分群特征指标，通过设定不同风速控制区间的聚类指标，通过K-means聚类方法进行聚合。用聚合后的单台或是多台风电机组表征整个风电场的次同步特性。具体实施步骤如下：

1）根据风电场的实际运行状态，确定风电场内的风机位置和电气连接网络，确定每台风机的风速和输出功率控制区间。

2）根据风机的实际运行状态，将风机划分在不同控制策略区域的风机集合。

3）利用下文所提出的K-means方法将分在同一集合内的风机相关参数聚合。具体实施步骤[27]如下：

①从所需分类的风机风速数据集合D中随机取k个元素，作为k个簇各自的中心；

②分别计算风机风速集合D中剩下的元素到k个簇中心的相异度，用欧式距离表示相异度，相异度越小，则说明二者之间越相似，将这些元素分别划归到相异度最低的簇；

③根据聚类结果，取簇中所有元素各自维度的算术平均数重新计算k个簇各自的中心；

④将D中全部元素按照新的中心重新聚类；

⑤重复第④步，直到聚类结果不再变化，输出每个聚类的结果。

4）得出每组聚类中的风电机组编号，用于后一部分的机组间的集电系统等值。

其简化流程如图2所示。

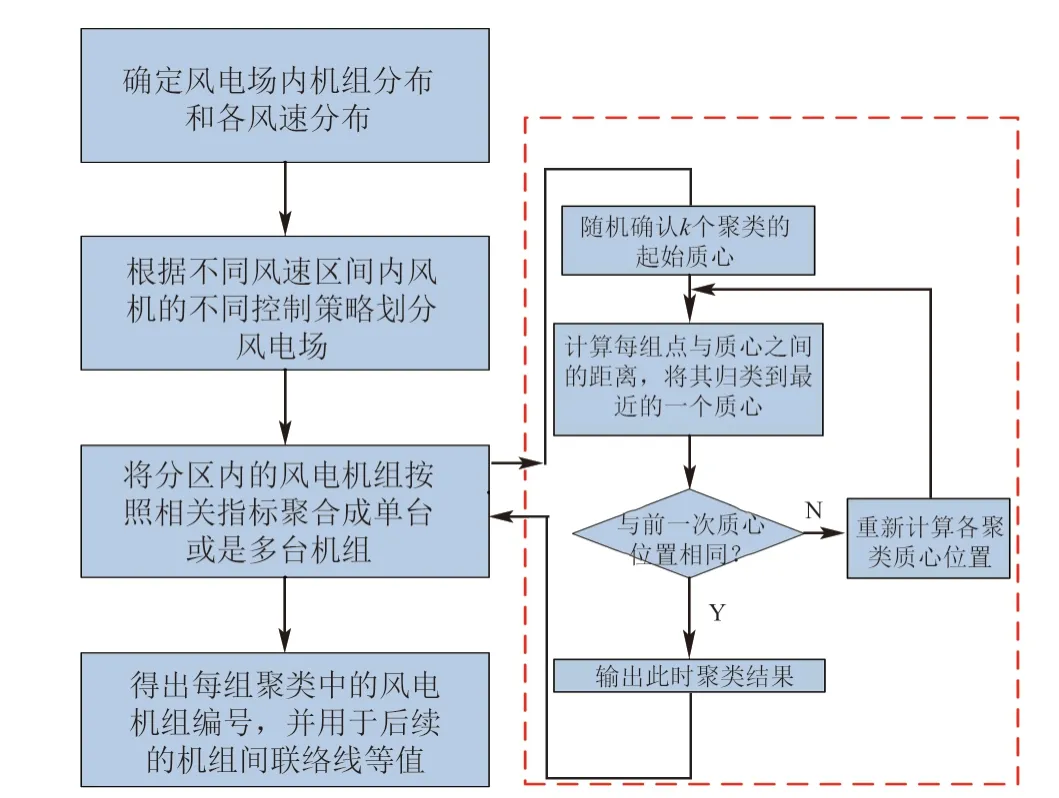
图2 大型风电场风机等值聚合流程图Fig.2 Equivalent flowchart of wind turbines in a large wind plant

2.3 风电机组的数学模型聚合

2.3.1 风电机组的涡轮机模型聚合

首先将同一聚类分组内的n台风电机组等值为一台风力机模型和一台发电机模型。风力机模型从风中所能吸收的风能表达式[16]为

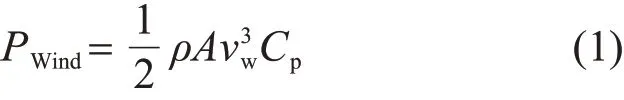
式中：PWind为风力机能够取用的机械功率；ρ为空气密度，通常取1.225 kg/m3；A为风机叶轮扫掠面积；Cp为风机叶片的功率系数，其值与叶尖速比和桨距角有关，小于贝兹极限值0.59；vw为风力机所在位置的风速。

假设风电机组的总发电效率为η(计及叶片捕风系统、发电系统和控制系统的各种效率)，则

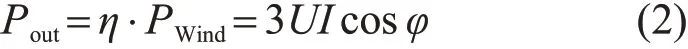
式中：Pout为单台风电机组出线端功率；由于双馈风电机组控制策略为单位功率因数控制，可以认为cos φ=1；U和I分别为出线端的相电压和相电流。

当实际风速≥额定风速时，风电机组输出为额定功率，输出端电流为额定电流；而当实际风速<额定风速时，单台风机出线端电压一定，其出线端电流幅值则为

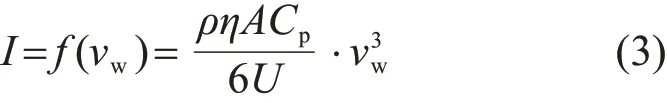
由式(3)可知，电流是风速的三次函数，每台机组出线端电流的大小可以用风速来表示。

当风电场内各个机群分组内所捕获的风速不同或者输出功率控制不同时，可以根据每个机群内各风机的风速与输出功率的关系式，求解出等值风机的等值风速，即

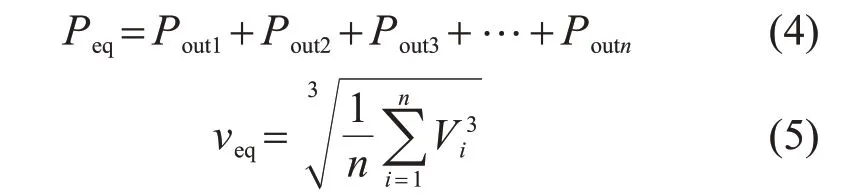
式中：Peq为等值功率；veq为等值风速。

在每个聚类的分组内，将所有的风电机组的风轮模型聚合到单台，以简化相应的聚类里的风电机组的风轮模型。

2.3.2 风电机组的发电机模型聚合

风机发电系统主要是将传动系统传递过来的机械功率转换为电磁功率，同时将控制系统给出的机械转矩指令转换为电磁转矩作用在传动轴上。在以标幺值表示的发电机参数下，聚合前后的相关参数在数值上相等，即其发电机参数聚合后为：

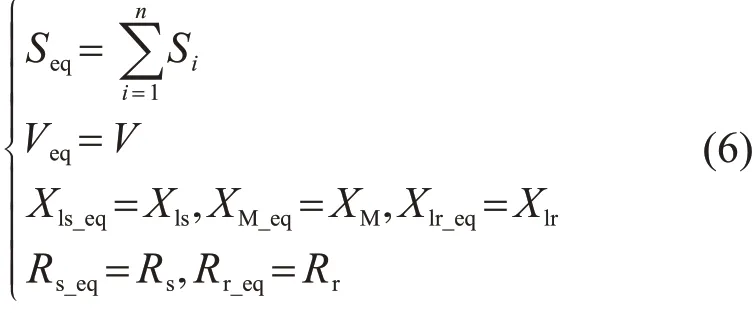
式中：Seq为等值发电机额定功率；Si为发电机i的额定功率；Veq为等值发电机额定电压；V为发电机额定电压；Xls_eq和Xlr_eq分别为等值发电机定子漏抗和转子漏抗；Xls和Xlr分别为发电机定子漏抗和转子漏抗；XM_eq为等值发电机励磁电抗；XM为发电机励磁电抗；Rs_eq和Rr_eq分别为等值发电机定子电阻和转子电阻；Rs和Rr分别为发电机定子电阻和转子电阻。

等值发电机容量由于聚合而增大，其等值后变流器的容量扩大为原来的n倍，风机变流器直流稳压电容等值为Ceq=nC，其直流侧等值额定电压不变。

3 风电机组间集电系统的聚合等值

3.1 大型风电场内风电机组空间分布

在每个聚类区间内的风电组被等值为一台或多台等值机组时，风机间的联络线路也需要进行相应的等值聚合。风电场布置要求风机在盛行风向上间隔5~9倍风轮直径，在垂直于盛行风向上要求机组间隔3~5倍风轮直径[28]。由于风机捕获的风能正比于其半径的平方，额定功率越大的风机间距也就越大，对于一台容量为5 MW的风电机组，其水平间距应在0.65 km以上。一个大型的风电场通常拥有数十甚至数百台兆瓦级的风电机组，风电机组数量越多的风电场，其内部集电线路也就越长，其内部集电系统对风电场输入电网的功率振荡特性会有较大影响。

大型风电场内风电机组大致空间分布如图3所示，既有链式串联部分，也有并联部分。

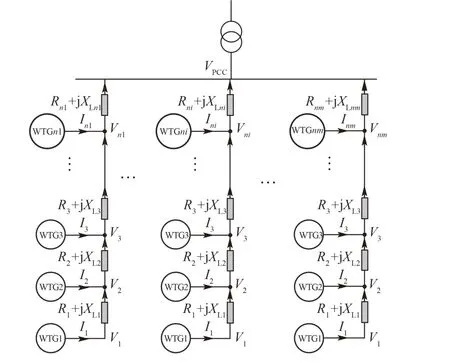
图3 大型风电场风电机组空间排布图Fig.3 Arrangement of wind turbines in a large wind plant

3.2 链式串联等值建模分析

在风电场内，其链式串联机组如图4所示，且认为每台风电机组出线端变压器均为其发电机组的一部分。因此，只需考虑所需等值的集电系统阻抗。

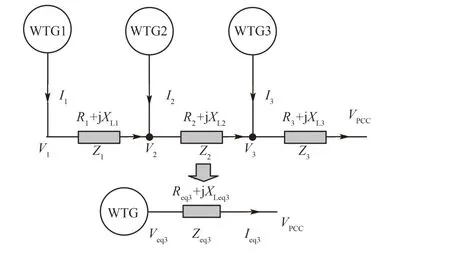
图4 串联式风电机组等值图Fig.4 Equivalent modeling of series wind turbine chain

如图4所示，以3台机组为例，设第1,2,3台风电机组出线端电流分别为：

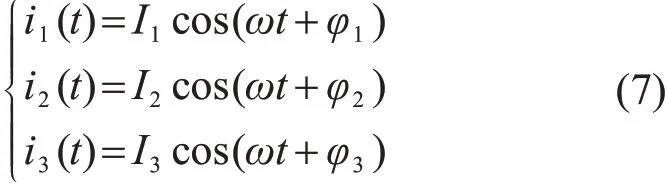
式中：I1,I2,I3分别为3台机组的电流峰值；φ1,φ2,φ3为电流对应的相位。

则有

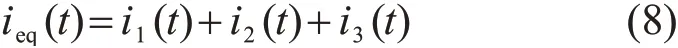
将式(7)代入式(8)，化简后可得：

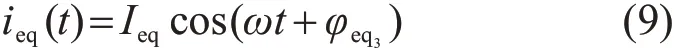
式中：Ieq=，φeq3=arctanB3/A3，A3=Ijcos(φi-φj)]。

而每段集电线路的功率消耗可以表示为：

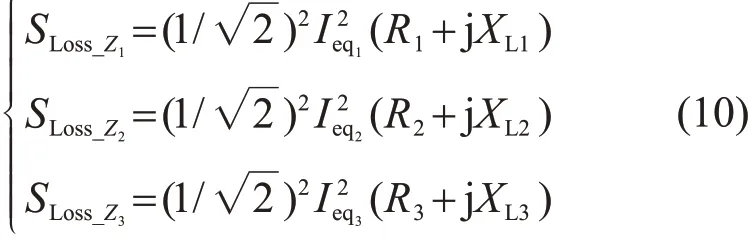
式中：Ieqi(i=1,2,3)为流经线路各段电流的峰值；Ri，XLi分别为线路电阻、电抗。

消耗的总功率表示为

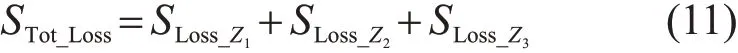
根据所提出的功率等值的原则，等值前后集电系统消耗的功率应该相等。因此，等值后消耗的总功率亦可以表示为

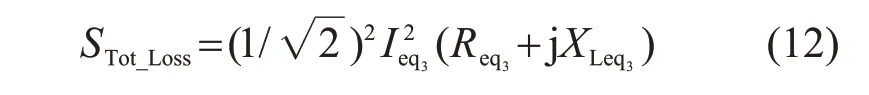
连列式(9)—(12)，求得Req3,XLeq3的表达式为：

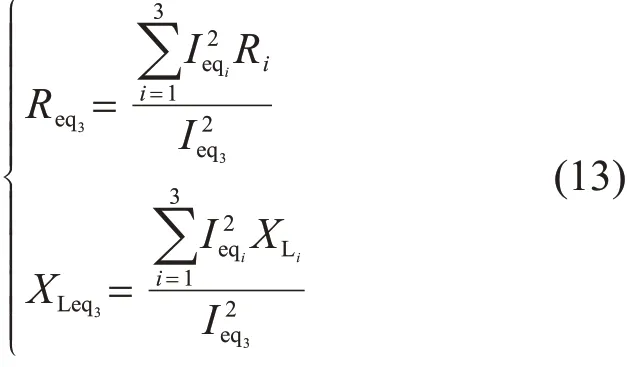
推广至n台风电机组链式串联，其等值后的阻抗可以表示为：

当所需聚合的n台风电机组的风速近似相等时，根据式(3)，可以认为其出线端电流幅值近似相等，即I1=I2=I3,…,=In=I。此时：

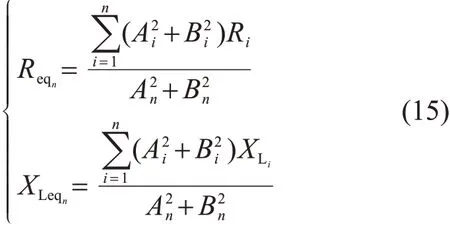
当所需聚合机组风速不完全相同时，当某台机组所捕获的风速vi大于额定风速vm，且小于切除风速时，以vm计算，则根据式(3)，出线端的电流幅值可以表示为：

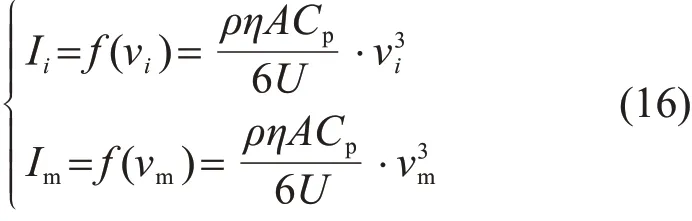
由式(16)可求出Ii=∙Im。此时，式(14)仍可以简化为式(15)的形式，但此时式中An=

3.3 链式并联等值建模分析

风电场内的并联式简化图如图5所示。与链式串联等值处理方法相同，将风机发电机出线端变压器看作一个整体，所以只需考虑集电系统联络线路阻抗的聚合。

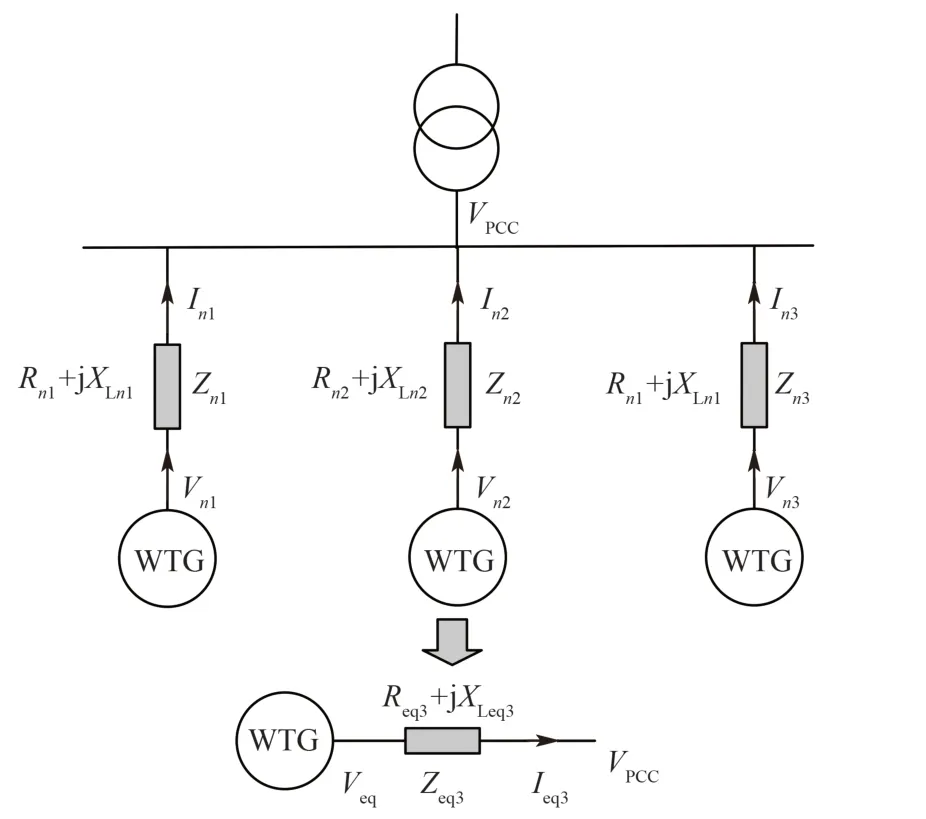
图5 并联式风电机组等值图Fig.5 Equivalent Modeling of parallel wind turbine chain

并联风机的等值与链式串联风机等值的推导过程相同，等值原则也是等值前后所消耗的功率恒等。

如图5所示，以3台机组为例，设第1,2,3列风电机组(包括已聚合的)出线端电流分别为：

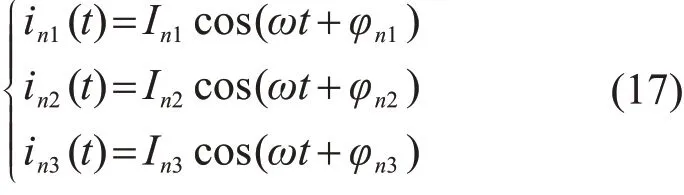
式中：In1,In2,In3分别为3台机组电流的峰值；φn1,φn2,φn3分别为3台机组电流对应的相位。

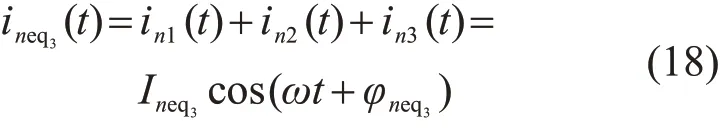
根据前述的等功率原则，等值前后集电系统消耗的有功功率和无功功率相等，并推广至m列风电机组等值，集电系统等值阻抗可表示为：

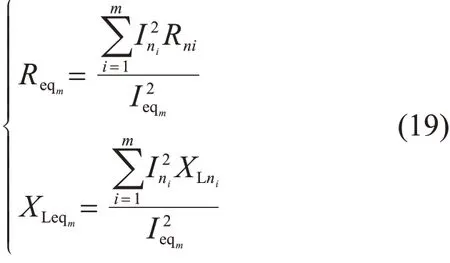
式中：Ini(i=1,2,…,m)为流经线路各段电流的峰值；Rni、XLni分别为线路电阻、电抗。

当等值前出线端电流近似相同时，式(19)可以简化为：

当所需聚合机组风速不完全相同时，与串联等值相似，其表达式仍为式(20)。但其中参数Ci=其余参数不变。

3.4 链式串并联等值建模分析

当不同的链式串联与并联线路中有同一聚类分组的风电机组时，所选取的聚合方法依然是串并联功率等值的综合，核心思想也是等值前后集电系统消耗的功率相同。如图6所示，虚线框内是同一聚类分组内的3台机组。所选择的方法为链式串联与并联的综合，根据集电系统中所消耗的功率相同的原则，先求出每台机组对集电系统公共耦合点的串联阻抗值，之后再利用链式并联部分进行等值聚合即可。

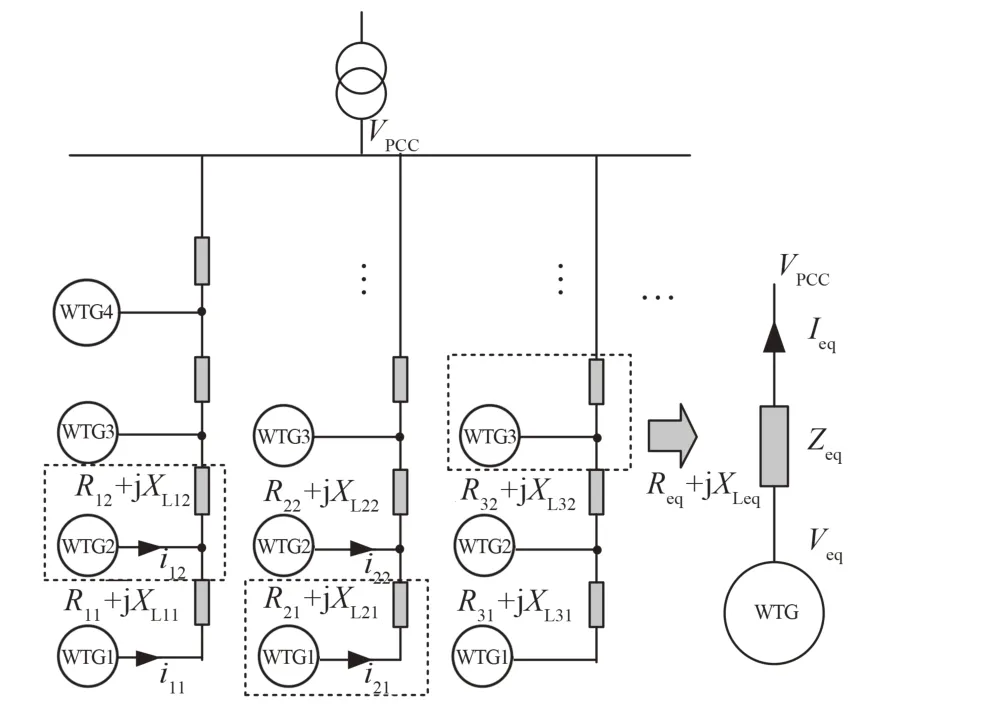
图6 串并共存风电机组等值图Fig.6 Equivalent modeling of series parallel wind turbine chains

4 算例分析

4.1 系统参数说明

本例参考某实际海上风电场，包括20台额定容量为5 MW同型号的双馈风机，风电场额定容量为100 MW，工频为60 Hz，切入风速为3 m/s，额定风速为11.5 m/s，切出风速为25 m/s。风机运行控制区域分为：低速恒转速区间3~5 m/s，最大风速跟踪区间5~11.5 m/s，恒转速恒功率区间11.5~25 m/s。风机额定输出端电压为690 V，经机端变压器升压35 kV，通过联络线路接于汇流母线，再经过主变升压至220 kV接入系统。设风机的叶轮直径为130 m，相邻风电机组间为1 000 m。每列间隔取为500 m。发电机的相关参数和架空线路参数分别如表1、2所示。假设风电场内风速均相同，为11 m/s，将所有的风电机组等值为1台机组，其简化示意如图7所示，风电场20台风机排列成5行4列。

表1 5 MW风电机组参数Tab.1 Parameters of the 5 MW wind turbine

4.2 算例分析一

如前所述，风电场包含20台额定容量为5 MW同型号的双馈式风机，总容量为100 MW，工频为60 Hz，风机与系统的各个参数如上所述，风电场内的排布图如图7所示，对各风电机组的风速进行实际测量，结果如表3所示，通过风速的聚类将集电系统等值为4台机组，即每列均是5台风电机组的等值机组，各列风电机组等值风速如表4所示，简化等值图如图8所示。

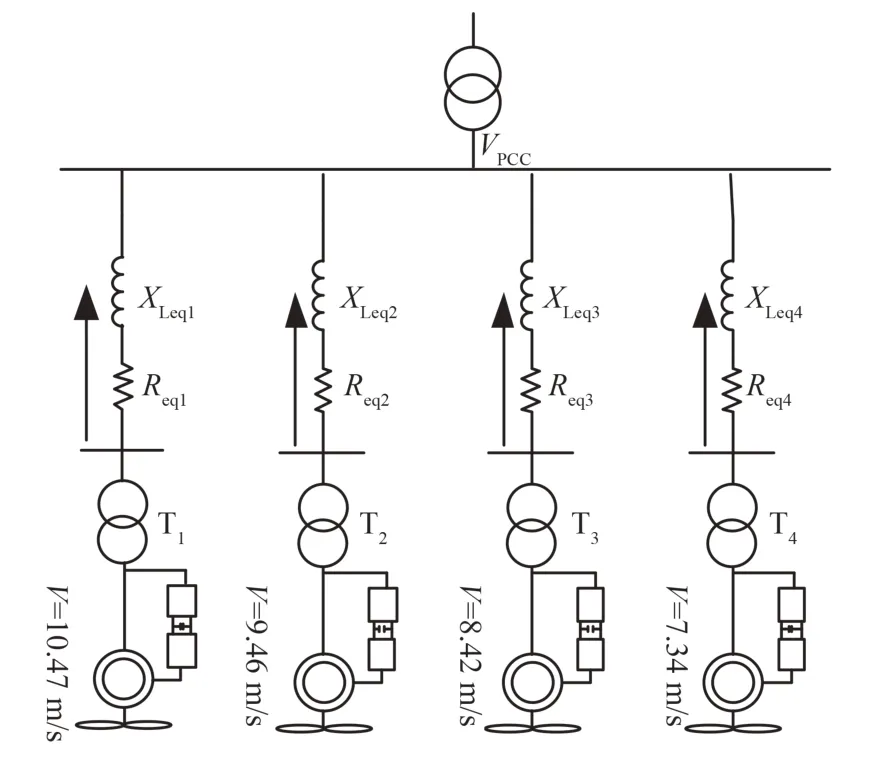
图8 风电场简化等值图Fig.8 Simplified arrangement of the wind farm

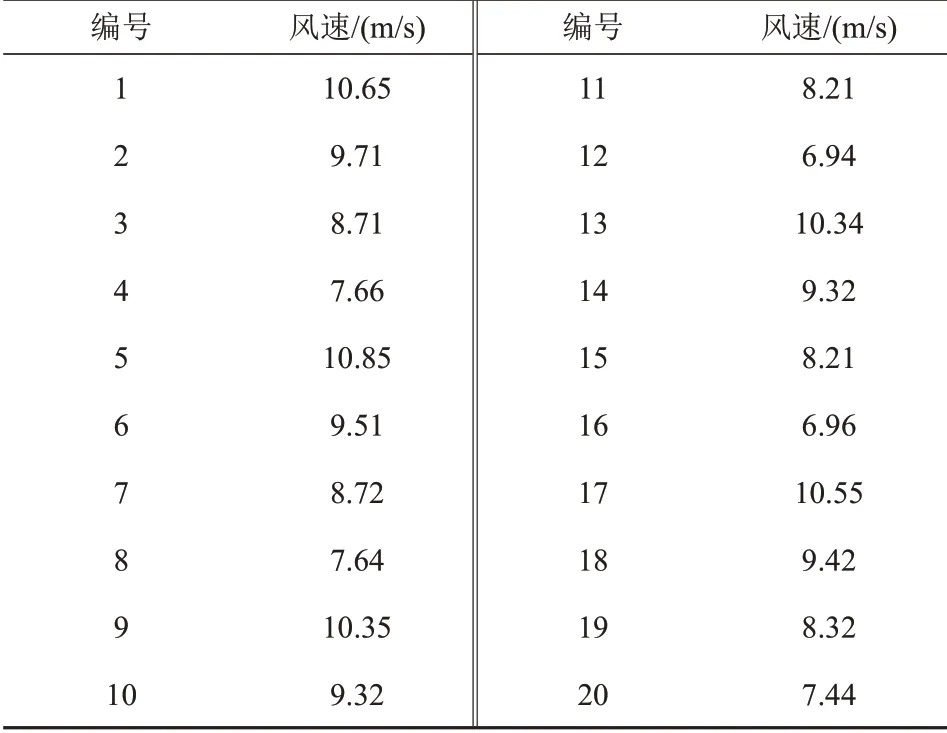
表3 各风电机组的风速Tab.3 Wind speed of each turbines in the plant

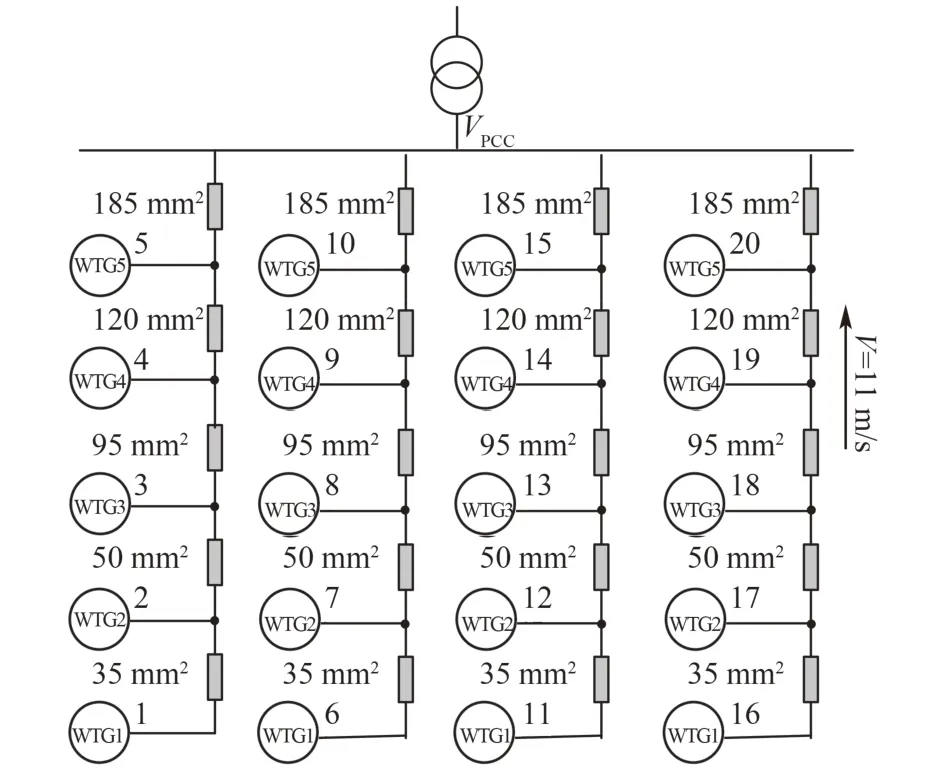
图7 风电场简化排布图Fig.7 Simplified arrangement of the wind farm

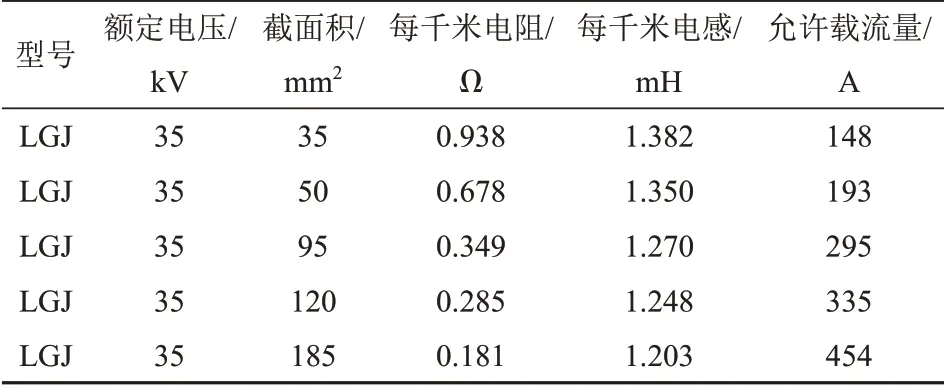
表2 35 kV线路参数Tab.2 Parameters of the 35 kV aerial conductor

风电机组的聚类简化模型由K-means聚类方法求出。在本算例中各风电机组风速不同，其电流幅值需要折算到额定风速下进行求解，等值风速由式(5)求出。同时根据等值前后的功率相同，通过前文所述方法由式(7)—(20)分别求解出等值阻抗值，如表4所示。在PSCAD/EMTDC中建立风电场未简化的详细模型，并同时搭建其等值仿真模型，对比分析等值前后系统的次同步特性。

表4 最终等值后的风速与阻抗值Tab.4 Wind speed and impedance after final equivalence

在PSCAD/EMTDC仿真平台建立图7原模型和图8等值模型，运行时间3~3.5 s施加一个激励，分别对比二者在稳态情况下的有功和无功功率误差，用Prony分析和傅里叶分析来分析暂态功率的次同步模态分量。等值前后风电场出线端的有功和无功功率如图9所示。等值前后稳态阶段风电场公共接入点PCC的有功、无功功率近似相等。在3~3.5 s施加一个激励后，对风电场PCC点的有功和无功功率进行Prony分析，均出现了44 Hz左右的负阻尼次同步振荡分量。同时对等值前后PCC点的电流进行傅里叶分析，结果分别如图10、11所示，可以发现，PCC点电流中存在16 Hz左右的主导次同步振荡分量，且其他各频率电流幅值含量很小。这也说明在分析次同步振荡时，功率等值能够较好近似原系统的次同步振荡分量。

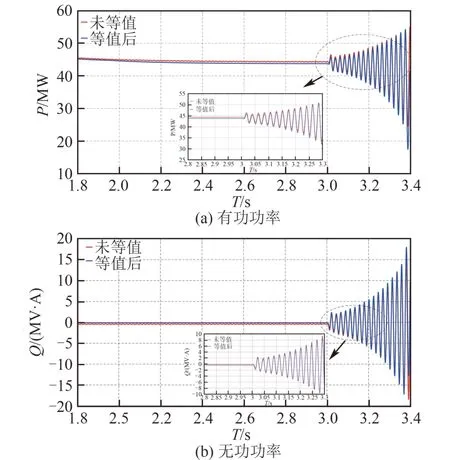
图9 等值前后风电场出线端有功、无功对比图Fig.9 Comparison of active and reactive powers between detailed and simplified models

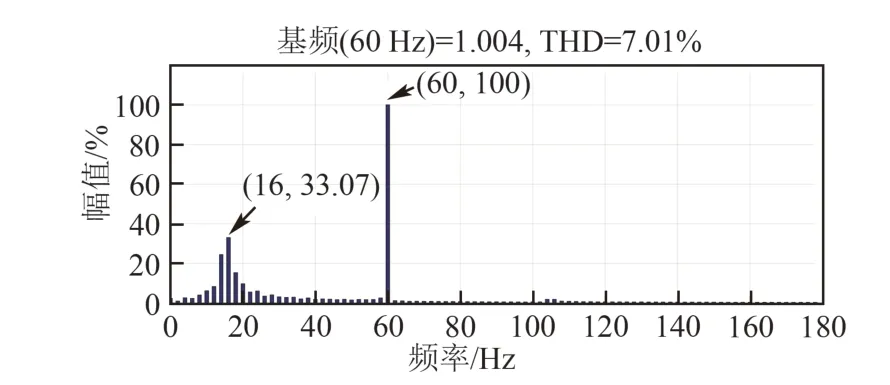
图10 详细模型PCC点电流中各频率分量Fig.10 Different frequency components in current at the PCC of detailed model

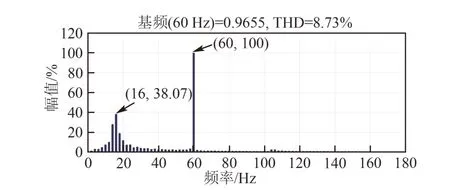
图11 等值模型PCC电流中各频率分量Fig.11 Different frequency components in current at the PCC of simplied model

设定仿真总时长为4 s，仿真时间对比如表5所示，可以看出，在实际时间中，详细模型运行需花费219 s，简化等值模型只需要27 s，简化等值模型很大程度上加快了仿真分析速度。

表5 仿真时间对比Tab.5 Simulation time comparison

4.3 算例分析二

当一个风电场内存在多个子风电场时，且各个风电场等值后的风速不同时，最简单的两子风电场的并联等值如图12所示，其等值阻抗可以表示为：Req+jXeq=(Req1+jXLeq1)//(Req2+jXLeq2)。

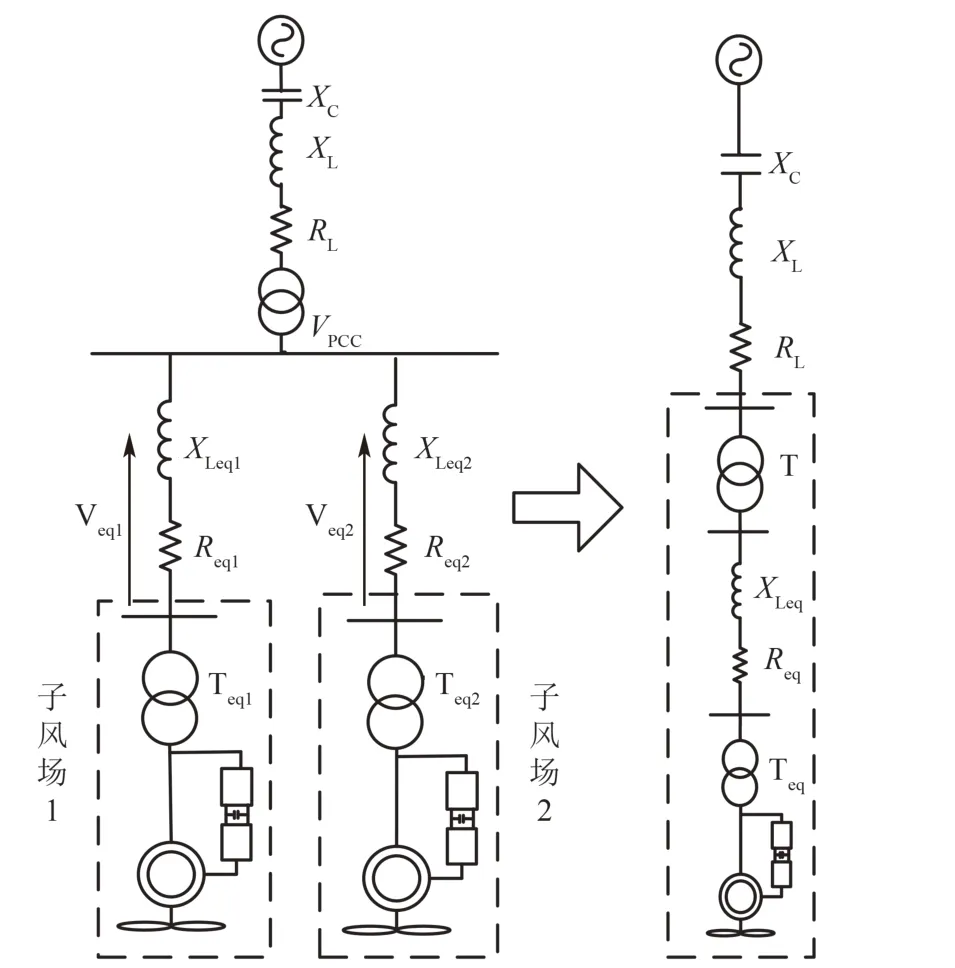
图12 两机组的并联等值示意图Fig.12 Equivalence of two sub wind plants

这种电路上的串并联等值的前提应该是风电机组出线端电压幅值和相位相同。但由于风电场内机组捕获的风速不同且集电系统的各个分支阻抗值不同，因此各台风电机组出线端电压幅值和相位不同。本算例中，通过功率等值和串并联等值对比20台风电机组的等值情况，每个子风电场中等值机组台数和风速如表6所示。每台机组出线端阻抗，串并联等值后阻抗和功率等值阻抗值如表7所示，在PSCAD/EMTDC中搭建该模型的详细模型和等值模型，取串补度为30%，分析对比其接入串补时次同步特性，分别如图13、14所示。

表6 各子风电场中风机台数和风速Tab.6 Number of wind turbines and wind speed in each sub-wind farm

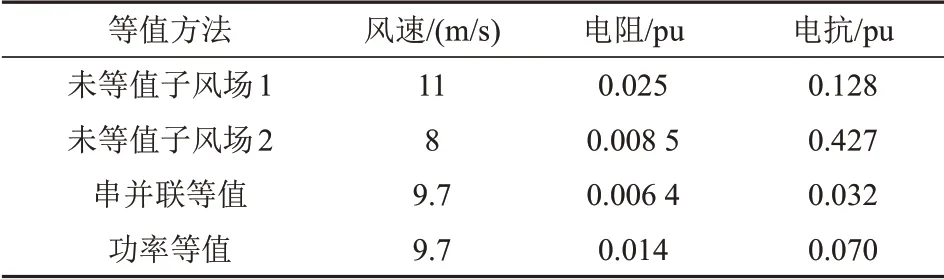
表7 不同等值方法的风速与阻抗值Tab.7 Values of different wind speeds and impedances using different equivalent methods

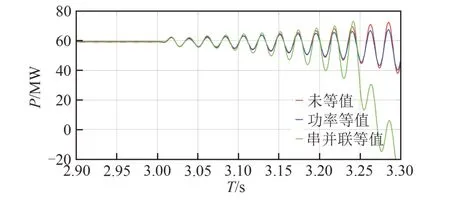
图13 接入串补时2种不同等值方式有功对比图Fig.13 Comparison of active powers between two different methods after connecting series compensation

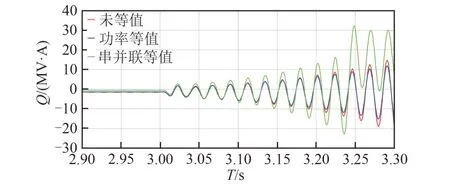
图14 被扰动后2种不同等值方式无功对比Fig.14 Comparison of reactive powers between two different methods after being disturbed

从图13、14中可以看出，串并联和功率等值在稳态下均能够较好地表征风电场的特性，但是串并联等值在次同步发生时不能很好地等值出整个风电场的动态特性，尤其是当等值的2个子风电场阻抗值相差较大时，这是由于并联等值的阻抗值必然小于最小的子风电场的阻抗值。然而，功率等值则克服了这一问题，能够更好地复现风电场的次同步特征。

5 结论

根据不同的风速指标，考虑各风电机组出线端电流不同，在此基础上聚合风电场内的集电系统，同时也对比了功率等值和串并联等值这2种简化等值方法。通过建立双馈风电机组的PSCAD/EMTDC详细模型和简化等值模型，对比在相同风速和不同风速2种情况下风电场发生次同步振荡时的主导功率振荡模态和各分量，以及功率等值和串并联等值，得出以下结论：

1）提出的功率等值的方法能够适用于风电场的简化仿真分析，减少计算复杂度，加快仿真分析速度。

2）功率等值在正常无故障运行时能有较好的等值效果。

3）在多机等值时，功率等值较串并联等值更能够表现出风电场次同步状态下的特性。

4）在发生次同步振荡时，通过Prony和FFT分析，发现功率等值较符合详细模型的次同步特性，复现其主导的振荡模态。