把握本质重基础 培育能力提素养
——对一道双曲线高考题的解法探究与思考
晏 鸿 (新疆教育科学研究院 830049)
符强如 (新疆乌鲁木齐市实验学校 830026)
2022年新高考数学全国I卷理科第21题秉承熟而不俗、俗中有变、变中有新的风格,注重数学本质和通性通法,彰显了从能力立意向素养导向的过渡,为学生提供了丰富的选择,是一道内涵丰富、解法多样的优质题,也为解析几何教学起到了很好的导向作用,值得一线教师去挖掘和探究.
1 题目呈现
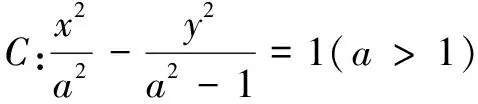
(1)求l的斜率;
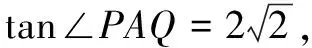
此题从问题表述来看,取材平实,表现朴实,题干清晰;从内容上来看,考查直线与双曲线位置关系、直线和双曲线平面图形(三角形)的面积问题.本题看似入手易、解法多,但命题者在多解背后都埋下了“地雷”,让它起到了压轴的功能,使不少学生力不从心,不能顺利完成解题过程.它考查了学生的逻辑推理、数学建模、数学运算等核心素养,要求考生需要具备较高的思维能力.
2 解法探究
思路1条件直译——代数法(这是解析几何教学中最常见的方法)
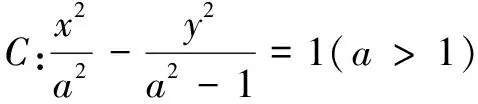

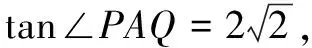
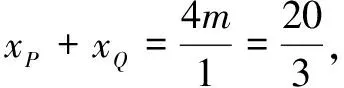


思路2条件转化——代数法
解析几何的拦路虎之一就是繁琐的代数变换,需要较强的运算能力.我们可以在思路1的基础上优化解法,将条件kAP+kAQ=0转化替代.
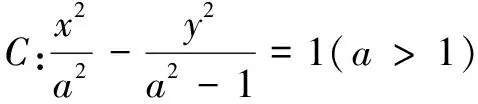


思路3参数法
运用参数方程能够快速解决圆锥曲线的弦长、范围等问题.


对于参数法解决圆锥曲线问题,也可以从以下视角来解决.
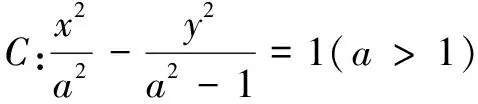
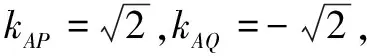
评注 参数法比传统方法具有更大优势,其核心就是减少了变量或参数.此题借助直线参数方程或双曲线相关的参数方程,从两个不同视角解析,利用参数t的意义解题,解法3和解法4视角不同,呈现的解析难度也不同.这也启示我们,变换解题视角去思考能够在一定程度上使解题思路“柳暗花明”,从而大大优化运算.
思路4齐次化联立
圆锥曲线问题中遇到斜率和或积的问题时,可以尝试齐次化联立.
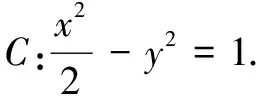
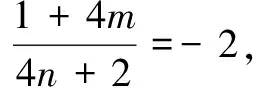
评注 齐次化联立即将直线方程与圆锥曲线方程联立后,利用“1”的代换实现齐次化,可以将题目中涉及的斜率转化成一个一元二次方程的两根,再由一元二次方程的两根关系获取斜率和或积的关系.但是此法一般是在解决圆锥曲线中直线斜率和或积的问题时应用,可以避免繁琐运算,提高解题正确率.
3 启示与思考
3.1 追溯背景

3.2 启示
当今的数学教育发展趋势可以理解为以理解为价值取向、以问题解决为价值取向、以数学探究为价值取向.教师要抓好课堂教学,在重视基础知识和基本技能教学的同时,更要注重提升学生对数学思想方法和数学本质的理解水平.对于此题,学生面对繁琐的步骤及复杂的计算往往都束手无策,容易产生畏难心理.其实“快”思维下数学教学更需要“慢” 艺术,不是单纯将教师个人认为好的数学思想方法短时间内打包发给学生,教师需要在课堂教学中 敢于等待学生,让学生独立思考、自主探索,发挥学生的主观能动性,陪伴学生重走数学知识的形成之路.
波利亚说过,没有任何一道题目是彻底完成了的,总还会有些事情可以做,更重要的是解题后的回顾[1].对于思维量较大或者所谓的“难题”,教师教学中应引导学生思考如何恰当利用题目主干条件、如何优化解题过程、怎样优化代数运算、深入分析和探究;更要积极引导学生进行反思,深度挖掘试题的背景,理清命题者的意图,深刻揭示试题本质,这样才有利于学生夯实基础,将知识系统化、网络化.关注思维以及问题的本质,对于数学问题的把握、揭示和体验都是提升课堂有效性的关键.对于高考压轴题,唯有如此才能居高临下指导学生,培养学生关键能力,发展学生核心素养.
一道经典的问题可以引导启发学生多角度思考.通过不同视角的解题途径,多方位多角度去思考问题,我们可以领略到解析几何与其他知识的综合交汇及其灵活迁移运用.虽然解题方法不同,但核心思想始终围绕着解析几何本质和思想,由特殊到一般地寻找规律,探索解题的通性通法.当然,通性通法必须在数学思想的指引下渗透,而不是同类型题目的简单重复和操练.要积累活动经验,强化思考能力,真正进入深度学习,发展高阶思维,提升数学素养.
高考真题立足基础,传承稳定;在稳定的基础上进行创新,这种创新不是通过一成不变的试题呈现,而是立足教材,对教材中的例题、习题运用稳定的基础知识、经典的基本方法、深化的基本思想进行包装.现阶段,尤其是复习教学,回归教材是正道.回归教材不是简单地阅读教材,不是简单罗列知识、梳理方法,更不是对教学过程的简单重现,而是对学科知识脉络的建构、对教材编者意图的领悟、对教材隐性知识的挖掘、对学科知识本质的把握,在平时教学中指导学生要寻“根”究“本”.唯有如此,学生核心素养方能切实培养.

