黑河下游胡杨林生态系统土壤蒸发模拟改进

李 强, 贾 薇, 高冠龙, 刘思敏, 霍 娜

(1.太原师范学院地理科学学院, 山西 晋中030619; 2.山西工商学院, 太原 030006;3.山西大学, 太原 030006; 4.国家林业和草原局经济发展研究中心, 北京 100714)

干旱区约占地球陆地总面积的41.5%，且这一比例仍在持续扩大[1]。在全球气候变化的背景下，干旱区水资源分布格局的变化势必会影响生态系统内各组分间水循环的正常进行。蒸散发，包括植被蒸腾、土壤蒸发和冠层截留3个部分，是气象、水文和生态学中的重要参数[2]，也是植物与环境之间质量和能量交换的重要组成部分[3-7]，其准确量化对于干旱地区合理制定灌溉方案、提高生态系统水资源利用效率具有重要意义[8-9]。在干旱地区，由于降水资源较少且植被叶面积普遍偏低，冠层截留在蒸散发中所占比例极小而常被忽略。因此，干旱区生态系统的蒸散发常被认为是植被蒸腾和土壤蒸发之和，其中，土壤蒸发是土壤—大气界面水分运动的关键环节之一，也是生态系统耗水量的重要组成部分[10]，确定生态系统的土壤蒸发量及其变化趋势，对于揭示干旱地区生态系统水循环机理具有重要意义[11]。观测和模拟是确定土壤蒸发量的2种基本手段，其中，通过建立或优化模型等方法进行模拟，依靠内在的物理过程和动力学机制便可以有效表征土壤蒸发的时空变化过程，成为了该领域研究的热点。

土壤蒸发作为蒸散发的一部分，可通过蒸散发模型模拟计算。在众多蒸散发模型中，双源Shuttleworth-Wallace(SW)模型和多源Clumping(C)模型能够区分植被蒸腾和土壤蒸发的不同过程，可直接模拟土壤蒸发。C模型结构非常复杂，包含的参数数量很多，在模拟计算与准确参数化方面存在难度。相较而言，SW模型的应用研究较为广泛，学者们重点关注模型结构优化及参数化方法改进[12-15]。Li等[16]和董军等[17]以覆膜玉米为研究对象，假定裸土、地膜下土壤热通量与地表土壤热通量相等，进而对SW模型中土壤蒸发计算式进行优化。吴林等[18]将考虑了大气CO2浓度对玉米冠层影响的冠层阻力模型与SW模型耦合，模拟了玉米整个生育期不同生长阶段的土壤蒸发量。刘春伟等[19]在冬小麦乳熟成熟期采用最小气孔阻力代替单一最小气孔阻力，分时段修正了SW模型，结果显示可以有效降低土壤蒸发模拟的误差。上述学者就特定的物种或时段对SW模型中土壤蒸发的计算公式进行改进，不具有普遍适用性，且模型中参数的数量也没有显著减少。因此，在双源模型的基础上，针对其中土壤蒸发的计算公式进行改进，进而准确量化生态系统土壤蒸发，成为了亟待解决的关键问题。

黑河发源于祁连山山麓中段，是我国西北地区的第二大内陆河。20世纪80年代来，随着黑河中游经济社会的快速发展，水资源需求量急剧增加，中游正义峡下泄水量显著减少，下游额济纳绿洲植被大面积退化。胡杨是额济纳绿洲主要的建群种，也是典型的荒漠河岸林[20]，受限于极端干旱的气候条件及稀缺的地表、地下水资源，胡杨呈显著的稀疏分布的特点。蒸散发是胡杨散失水分最主要的途径，而土壤蒸发是其中无效的水分消耗环节，准确模拟量化胡杨林生态系统的土壤蒸发量，探究土壤蒸发在蒸散发中所占比例，对于揭示黑河下游胡杨林生态系统水循环机理具有重要意义。本文将Priestley-Taylor(PT)模型引入Penman-Monteith(PM)模型，进而推导出改进的土壤蒸发模型。该模型与SW模型中土壤蒸发的计算式相比，可以实现不考虑复杂阻力参数的蒸发模拟，有效减少了参数数量以改进模型结构。本研究旨在明晰土壤水分的变化情况及胡杨林生态系统水文循环过程，为黑河下游胡杨林的恢复与重建提供科学依据。

1 研究区概况

试验样地位于黑河下游额济纳绿洲达镇东南的七道桥胡杨林保护区(42°21′N，101°15′E，海拔高度为920.5 m)，保护区内共有胡杨样树80株，均为天然树种，树木长势良好。树龄约为34 a，树木平均高度为10.4 m，平均胸径为24.97 cm，平均冠幅为482 cm×494 cm。该区域海拔在 850～1 100 m，总地形向东北方向倾斜。年平均气温 8.6℃，年平均风速 4.4 m/s，全年 8级以上大风日数平均为 54 d。气候类型为极端大陆性气候，年平均降水量低于40 mm，而蒸发量却高达 2 500～4 000 mm，空气相对湿度不足35%，平均土壤含水量为30%，属极端干旱区。

2 研究方法

2.1 试验设计

试验于2016年胡杨主要生长季内(5月—10月初)进行。在试验样地中部设有一个涡度相关观测塔(高度为24 m)，安装有一套开路式涡度相关测定系统(安装高度为20 m)，由三维超声风速系统(CSAT3，Campbell/美国)和开路式CO2/H2O红外分析仪(Li-7500A，LI-COR/美国)组成，用于测定胡杨林生态系统蒸散发。另有一些气象传感器安装于观测塔的不同高度处，包括四辐射仪(CNR4，Kipp & Zonen/荷兰，安装高度为10 m)、大气温度传感器(HC2S3，Campbell/美国，安装高度为4 m)、光合有效辐射仪(LI-190 SA，LI-COR/美国，安装高度为6 m)。土壤热通量板(HFP01，HUKSEFLUX/荷兰，2块)埋设于地下0.05 m处，土壤水分探针(SMC300，Spectrum/美国)埋设于地下0.1 m，0.3 m，0.5 m，0.8 m处。

样地内有5套微型蒸发器埋设于土壤中，微型蒸发器由PVC管加工、内外套管组合而成，内管高度为150 mm，壁厚为3 mm，内径为100 mm；外管内径为120 mm，固定于土壤中，方便取出和放回内筒，也能够避免更换土壤时对周围土体的破坏。用微型蒸发器取原状土样时，首先将内管垂直压入土中，然后带土整体挖出后用保鲜膜封底，用皮筋及胶带固定。在试验期内每月选择3～5个无降水观测日(5—9月为胡杨生长季的展叶期、果期和种子散播期，蒸散发量大，每月初选择5 d进行观测；10月初胡杨进入叶变色期，蒸散发减弱，选择3 d进行观测)，从8：00—18：00每隔1 h用精度为0.01 g的电子天平测定1次微型蒸发器的质量，记录各蒸发器相邻2次质量的差值并取平均值，即为该时段内的土壤蒸发量。

在试验期内每月选择1 d，运用植物冠层分析仪(LAI-2200，Li-COR)测定胡杨林叶面积指数(LAI，m2/m2)。植物冠层分析仪选用10°遮盖冒，在没有胡杨冠层遮盖的地方读取1个A值，然后在冠层下不同的点位读取4个B值，重复操作3次，取平均值即为该月胡杨林的叶面积指数。各仪器测定的参数见表1。

表1 样地内各仪器测定的参数

2.2 涡度数据处理

首先运用Loggernet 4.0软件对原始数据进行分割及格式转换，然后用Eddypro 5.2.0软件对分割后的数据进行倾斜校正、频率响应校正、时间滞后校正、超声虚温校正、密度效应校正及异常值剔除等处理。对于原始数据的分析，处理方法来源于Vickers和Mahrt[21]，而数据的质量检查则依据CARBOEUROPE标准。数据经上述过程处理后，仍然存在异常值，包括降水时次的数据、Rn<10 W/m2的数据以及λET>800 W/m2的数据，对其进行进一步剔除并插补，具体方法为：2 h范围内的缺失数据采用线性内插法，大于2 h的缺失数据采用平均昼夜变化法[22]。

2.3 模型介绍

SW模型中模拟土壤蒸发量(Esw)的计算公式如下：

(1)

(2)

(3)

(4)

(5)

(6)

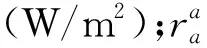
本文中各阻力参数的计算公式及文献来源见表2。

将PT模型引入PM模型，可推导出改进的土壤蒸发模型，模拟土壤蒸发量(Eimp)计算公式如下：

(12)

式中:Rn为净辐射(W/m2);G为土壤热通量(W/m2);αE为受光系数;τc为常数;τ=Rns/Rn(Rns为地表净辐射能量(W/m2)),根据比尔定律,Rns的计算公式为:Rns=Rnexp(-kLAI),k值取0.5[27];其余参数意义同上。

2.4 模拟精度评定

选用修正效率系数(E1)、修正一致系数(d1)和平均绝对误差(MAE)3个数据指标来评定模型模拟精度，计算公式为：

(13)

(14)

(15)

式中:Oi为实测土壤蒸发量(mm);Mi为模拟土壤蒸发量(mm);Oi为实测平均土壤蒸发量(mm);N为样本总数。

表2 各阻力参数计算公式及文献来源

式中:z为三维超声风速系统的安装高度(m);h为冠层平均高度(m);d为零平面位移(m);z0为粗糙度长度(m);k为Karman系数;z′0为裸露土壤的粗糙度长度(m);LAIs为确立参数时实测的叶面积指数(m2/m2);lw为叶宽(m);uh为冠层高度处风速(m/s);其余为经验系数。

3 结果与分析

3.1 不同月份胡杨林生态系统实测土壤蒸发及蒸散发均值日变化

将各月所有观测日内相同时段的实测土壤蒸发及蒸散发取平均值，以反映不同月份胡杨林生态系统实测土壤蒸发及蒸散发的日变化情况(图1)。可以看出，土壤蒸发和蒸散发各月的日变化均呈抛物线形趋势，日最大值出现在中午12：00—14：00的时段内；整个试验期内，土壤蒸发及蒸散发的最大值出现在7月份的正午时分(分别为0.3，0.6 mm)，而最小值则出现在10月初的清晨(分别为0.005，0.02 mm)。在6—8月各时刻的均值水平明显高于其他月份。

3.2 胡杨林生态系统蒸散发量变化趋势

基于涡度实测蒸散发数据，将每天8：00—18：00每小时的数据求和，即为当日胡杨林生态系统蒸散发。试验期内胡杨林生态系统蒸散发变化情况见图2。可以看出，蒸散发整体上呈先升高后降低的趋势，总量为826.7 mm。最大值出现在6月中旬，为8.9 mm；最小值出现在5月初，为2.1 mm。各月份蒸散发的平均值依次为4.2，5.8，5.6，5.1，5.3，4.0 mm。

3.3 胡杨林生态系统土壤蒸发在蒸散发中所占比例的变化趋势

在实测土壤蒸发的观测日内，计算土壤蒸发与蒸散发的比值，分析其变化趋势以及与叶面积指数的对应关系(图3)。可以看出，试验期内土壤蒸发与蒸散发比值的变化范围为30.2%～72.2%，胡杨生长季初期(5月)该值最高，而8月—10月该值相对较低(均低于40%)，其变化趋势与叶面积指数大致相反。

图1 不同月份胡杨林生态系统实测土壤蒸发及蒸散发日变化

图2 胡杨林生态系统蒸散发的变化趋势

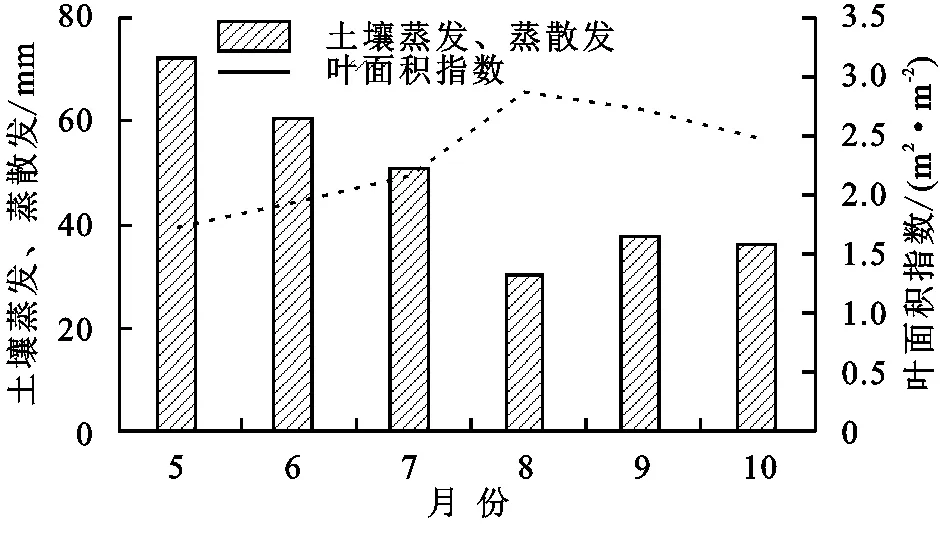
图3 胡杨林生态系统土壤蒸发在蒸散发中所占比例的变化趋势

3.4 胡杨林生态系统土壤蒸发模拟改进

分别基于SW模型和改进的双源模型中土壤蒸发的计算公式，模拟胡杨林生态系统土壤蒸发量，二者的变化趋势和对应关系分别见图4—5。图4中，对比实测土壤蒸发和分别基于SW模型、改进双源模型模拟的土壤蒸发，计算平均绝对误差分别为0.019(改进双源模型)和0.037(SW模型)，可以看出改进的双源模型模拟土壤蒸发的效果更好。同时，结合本文选用的模拟精度评定指标，进一步对比分析上述2个模型的模拟精度(表3)。可以看出，基于改进的双源模型模拟土壤蒸发的E1，d1和R2的值(0.71，0.85，0.92)均大于SW模型各值(依次为0.44，0.71，0.66)，而MAE的值(0.02)小于SW模型(0.04)，也更加表明改进的双源模型具有较高的模拟精度，更适于模拟胡杨林生态系统土壤蒸发。

采用Zhan等[28]提出的敏感性系数法对模拟精度较高的模型参数进行敏感性分析：

式中:Sp为敏感性系数；E0,E-和E+分别为各参数值取P0,1.1P0,0.9P0(P0为各参数原始数值)时对应的土壤蒸发值。针对模拟精度更高的改进的双源模型中土壤蒸发量的计算公式,对其参数敏感性进行分析,结果见表4。

图4 实测土壤蒸发和分别基于SW模型、改进双源模型模拟的土壤蒸发变化趋势

图5 基于SW模型(A)和改进双源模型(B)模拟的土壤蒸发与实测结果对比

表3 基于SW模型和改进双源模型的模拟精度对比

表4 改进的双源模型中土壤蒸发量计算公式的参数敏感性分析

可以看出，改进的双源模型中土壤蒸发量的计算公式对于净辐射的敏感系数值最高(0.18)，说明模拟土壤蒸散量对净辐射最为敏感。

4 讨 论

土壤蒸发是陆地—大气之间能量交换的一个主要过程，气象条件是土壤蒸发的驱动因子[29]。本研究重点分析了净辐射、光合有效辐射、大气温度和风速与土壤蒸发及蒸散发的相关性(表5)。结果表明，各环境因子与土壤蒸发、蒸散发的相关性大小依次为：净辐射>光合有效辐射>大气温度>风速。净辐射与土壤蒸发及蒸散发的相关系数最大(分别为0.905，0.693)，这与刘丽霞[30]、刘国水[31]、李菊[32]、吴友杰[33]等的研究结果一致。从土壤蒸发日变化情况来看(图2)，在午间(12：00—14：00)时段内土壤蒸发速率较高，与韩生生等[34]研究结果一致，这进一步说明土壤蒸发主要受净辐射的影响(午间净辐射高，土壤蒸发量大)。此外，李伦[10]、穆家伟[35]等研究发现，湿润环境条件下土壤蒸发与净辐射相关性显著，而干旱条件下二者相关性较差。在本研究中，研究区虽处于极端干旱区，但是胡杨为典型荒漠河岸林植物，以吸收地下水作为水分补充的重要途径，而黑河在分水工程实施后，下游地表水量显著增多，对于地下水资源起到了很好的补给作用。样地内胡杨没有面临缺水的情况[36]，土壤蒸发与净辐射显著相关，说明净辐射相较其他环境因子而言，对土壤蒸发的变化影响最直接。此外，由表4看出改进的双源模型对于净辐射的参数敏感性系数最大，说明净辐射的准确测定对于土壤蒸发的模拟精度至关重要，在实际工作中需对其进行精确测定。

表5 土壤蒸发、蒸散发与主要环境因子(净辐射、光合有效辐射、大气温度和风速)相关性

在蒸散发的组分中，冠层蒸腾通常与植被生产力有关，而土壤蒸发并非直接对生产力作出贡献[37]。因此，过往对于干旱地区荒漠河岸林生态系统水分利用特征的研究主要集中于植被蒸腾[38-40]或蒸散发[41-44]，而对于土壤蒸发的量化及其与蒸散发的比例研究则较少。本研究中，胡杨林生态系统土壤蒸发在蒸散发中所占比例的变化范围为30.2%～72.2%(图4)，符合Wilcox等[45]总结的干旱半干旱地区供水良好条件下该比例的变化范围(30%～80%)，且最大值(72.2%)与Su等[46]同样针对黑河下游胡杨林生态系统中土壤蒸发/蒸散发计算得出的最大值(79%)也较为接近。Yu等[47]研究发现，黑河下游胡杨林生态系统中土壤蒸发对于下泄地表水量的响应程度显著高于冠层蒸腾，因此合理确定土壤蒸发在蒸散发中所占比例，对于优化黑河下游地表水灌溉防范具有重要意义。此外，本文研究结果显示胡杨林生态系统土壤蒸发/蒸散发与叶面积指数的变化趋势大体相反(图4)，原因在于随着叶面积指数的增大，胡杨蒸腾作用逐渐强烈，在蒸散发中所占比例增加，相应地土壤蒸发所占比例减小。

土壤蒸发是陆地水文循环的重要组成部分[48]，其对土壤温度的影响使得利用土壤温度变化估算土壤蒸发成为可能。因此，以往学者们基于土壤温度变化开展了生态系统中土壤蒸发的估算研究[49-52]。本研究从蒸散发模型模拟的角度，针对传统双源SW模型中土壤蒸发的模拟方法进行改进，与基于土壤温度变化模拟土壤蒸发的方法相比，有利于开展生态系统蒸散发的区分研究，具有更好的应用性。对比分析SW模型与改进后的土壤蒸发模型的模拟结果，可以看出SW模型模拟精度略低(表3)，原因在于其模型结构相对复杂，包含参数较多，各参数的准确量化较为困难，其不确定性往往又导致模拟结果的差异。而改进后的土壤蒸发模型在模拟计算时，可以不考虑诸多复杂阻力参数的计算过程，模型结构与参数数量均得到了明显优化(只包含净辐射、地表净辐射、土壤热通量和叶面积指数等实测参数以及受光系数等拟合参数，均为极易量化的参数)，模拟精度也更高。但是该方法目前只是针对黑河下游胡杨林生态系统中土壤蒸发进行的模拟，其一般规律还有待进一步验证。

5 结 论

本文基于黑河下游额济纳绿洲七道桥胡杨林保护区实测数据，分析了胡杨林生态系统中土壤蒸发和蒸散发的变化趋势及其与环境因子的相关性，通过SW模型和改进的双源模型中土壤蒸发的计算公式对其进行模拟，对比分析了各模型的模拟精度及参数敏感性，得到的主要结论如下：(1) 土壤蒸发和蒸散发各月的日变化及整个试验期内的变化均大致呈先升高后降低的趋势；(2) 胡杨林生态系统土壤蒸发在蒸散发中所占比例的变化范围为30.2%～72.2%；(3) 改进的双源模型中，土壤蒸发的计算公式可以不考虑复杂阻力参数的计算过程，且与传统的双源SW模型相比具有更高的模拟精度；(4) 净辐射对土壤蒸发的影响最显著。