指向思维提升的“问题串”教学实践探究
雷 丽
(江苏省扬州市特殊教育学校,江苏 扬州 225000)
问题教学被广泛应用于数学课堂。近年来,“问题串”教学法越来越受到关注。《中国教育学会中学数学教学委员会中学青年数学教师优秀课评价标准(修订版)》(试行稿2012 年)中明确提出:在教学策略方面,围绕教学重点,依据知识的发生、发展过程和学生的思维规律设计“问题串”以引导学生的数学思维活动的分析。相较于单个问题来说,“问题串”的确能够启发学生持续思考,促进学生思维持续深入。那么,如何开展“问题串”教学提升学生数学思维?本文将结合实践,从教学理念、设计与实践、教学反思三方面进行论述。
一、指向思维提升的“问题串”教学理念
纵观指向思维提升的“问题串”教学,其中包含了两个重要元素:问题串、思维。其一,“问题串”是指聚焦目标,按照一定逻辑结构精心设计的一组问题。这组问题至少包含3 个单问题,类别有递进式问题串、平行式问题串和辐射式问题串等。其二,“思维”是指数学思维能力,即学生在生活中应用数学知识和数学技能分析、思考及解决问题的能力。数学思维遵循从直观动作思维到形象思维再到抽象思维的一般规律,同时具有抽象、归纳、类比、推理等特殊特征。
综合上述两大元素的具体内容不难看出:指向思维提升的“问题串”教学,就是指在数学课堂教学中,立足学生“最近发展区”,关注知识发生、发展规律,精心设计符合要求的问题串;课上教学时采用合适的教学方法在恰当时机向学生依次提出,引导学生深度学习,促进学生自主建构,提升学生思维能力的综合性实践过程。在这个过程中,教师们不可忽视三个基本量,即学生认知、教学方法及最终目标。
1.问题串的设计要基于学生认知基础和认知特点。教学的主体是学生。问题串应从学生已有的认知基础出发,以“最近发展区”为值域,循序渐进地设计问题。根据实践,问题串设计的时机是学生认知上发生真正障碍的时候,即认知失衡的时候。之所以强调“真正的认知障碍”是为了防止伪问题串出现。问题串不是问题的简单组合,好的问题串能够体现数学学科本质。
2.课堂教学要采用合适的教学方法。问题串教学要采用规范、有效、受认可的教学方法,如直观教学法、多感官教学法、从特殊到一般教学法等。教师提出问题串的时机形式多样,可以在课堂引入、新课探究、课堂练习等环节提出,学生通过思考、口答、手写或操作等方式完成。问题串中每一个问题应保证班上大部分学生通过自主探究能够完成,教师要保护学生的探究欲望和探究信心。
3.问题串教学紧扣教学目标。“问题串”的价值不在于问题串本身,而在于驱动学生深度学习。所以,教师设计问题串时应围绕“为什么这么设计”以及“这么设计为了什么”这两个基本问题开展;教学问题串时应紧扣教学目标,凸显问题串价值,激发学生深度学习,拓展学生数学思维深度。
基于以上对教学理念的分析,为了更清晰说明“问题串”教学如何提升数学思维,笔者将分别以递进式问题串、平行式问题串、辐射式问题串三种类别进行阐述。
二、指向思维提升的“问题串”设计与实践
(一)教学递进式问题串,纵向提升思维
递进式问题串,由表及里、由浅入深、由易到难驱动学生带着问题主动学习、自我建构。递进式问题串中,前后问题相互关联,前一个是铺垫,后一个是继续,形成阶梯状的问题链。学生能够直观感知知识内在联系,从而达到纵向提高思维能力的目的(如图1所示)。
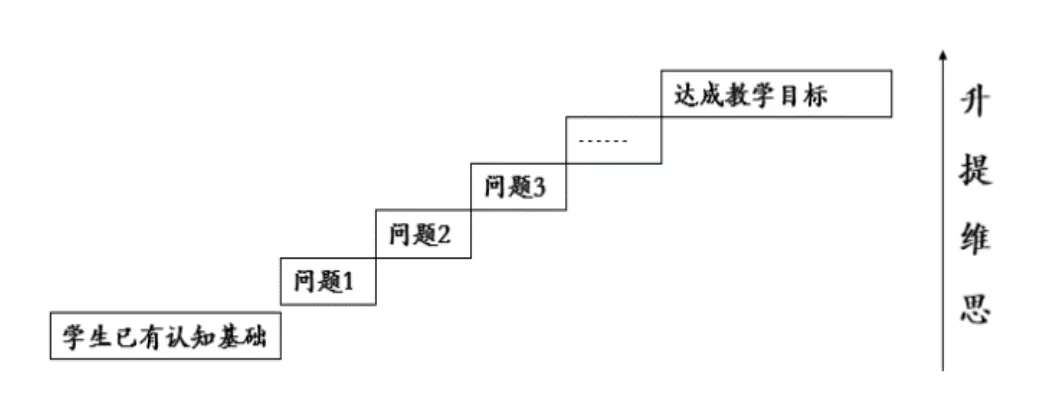
图1 递进式问题串教学,纵向提升思维
如,笔者教学人教版七年级下册《一次函数》起始课《函数与方程》时,根据学生认知特点,采用“从特殊到一般”教学法,设定“经历从特殊到一般的解题过程,对比算式解题和方程解题特点,感受方程解题的便捷”为知识与技能目标。为此,笔者设计了如下问题串:
问题1:6 点乘坐客车从扬州出发,沿着高速公路行使100km,7 点到达南京。
问题创设旅游情景,激发学生兴趣。
师:这个情景可以看成什么数学问题?
生:行程问题。
师:你们发现了哪些要素?
生:路程、时间,可以求出速度,速度为100km/h。
行程问题是学生比较熟悉的数学问题,从情境条件中容易发现行程三要素以及之间的关系。
问题2:6 点一辆私家车从扬州出发,沿着这条高速公路也行使100km,a 点到达南京。
师:你们又发现了哪些信息?
生:路程100km、时间(a-6)h,速度是V=100/(a-6)。
问题2 引入字母a,完成从特殊到一般的推广。经过问题1 和问题2,学生逐渐明白,要解决的问题其实就是一辆车从A 地到B 地的行程问题。
问题3:一辆汽车从A 地出发,行驶s km 到达B地,用时t h。
问题3 求得V=S/T,这也是学生小学阶段学习过的速度公式。随着问题的解决,学生进一步感受从特殊到一般,这也是算术法解方程问题的基础。
问题4:一辆客车和一辆私家车同时从A 地出发,沿着同一条公路同方向行驶,客车的行驶速度是70km/h,私家车的行驶速度是60km/h,客车比私家车早1h 经过B 地,A、B 两地间的路程是多少?
有了前面3 个问题的铺垫,此时只需要引导学生用算术法和方程法分别求解即可。最后教师提问:“你能比较用算术法和方程法解此题的异同之处吗?”鼓励学生辨析两种方法的异同点,感知列方程解题的便捷。
问题5:一辆客车和一辆私家车同时从A 地出发,沿着同一条公路同方向行驶,客车的行驶速度是b km/h,私家车的行驶速度是a km/h,客车比私家车早ch 经过B 地,A、B 两地间的路程是多少?
这个问题完成了初中阶段对行程问题的最一般化的要求。学生借鉴问题5,可以列出一个一元一次方程,对方程概念形成了最一般意义的解读。
如果在数学课堂中教师平铺直叙地教学,学生通常无法长时保持注意,学习氛围和教学效果都会大打折扣。而若教师改用“问题串”教学,学生在发现问题、解决问题的螺旋重复中,不断向着更高难度挑战,从中体验成功的喜悦,那么学习热情必然高涨。例如,在进行“三角形全等的判定”教学时,笔者采用“合情推理教学法”,设定教学目标为“理解三角形全等判定的方法,简单应用判定方法判定两个三角形全等”,设计如下“问题串”:
问题1:三角形的定义是什么?组成三角形的基本元素有哪些?
问题1 主要是复习旧知,引出新知,接下来将利用三角形的基本元素及其之间的关系探究三角形全等的判定方法。
问题2:全等是什么意思?全等三角形的概念是什么?
出示问题2,学生正确回答后,教师要求学生“举几个全等的例子”以及“动手画一组全等三角形”巩固旧知。学生调动记忆,回顾旧知,通过实例和动手画加深印象。
问题3:全等三角形有什么性质?
学生在解答问题2 时,已经动手画过一组全等三角形,加上全等三角形的性质是教材明确给出的,所以学生准确回答并不困难。此时,教师继续反问学生:
问题4:你刚才画的一组三角形一定全等吗?
学生无法保证所画两个三角形一定全等。这是批判性思维的雏形。进而教师自然引入“问题5:如何判定两个三角形全等?”这个终极问题,这也是整章教学的重点。
“一串”递进式的数学问题,让学生从三角形的概念、全等三角形的概念、全等三角形的性质自然过渡到三角形全等的判定。试想,如果教师课上直接向学生提出“三角形全等如何判定”问题,学生因未能及时链接旧知和新知,那么可想而知,下面的探究活动将变得非常缓慢。
(二)教学平行式问题串,横向提升思维
平行式问题串注重促进学生思维的横向发展。平行式问题串主要是指,教师围绕一个知识点设计若干问题,问题之间并无关联,没有梯度,不分主次,但它们的作用一致,均服务于教学目标(如图2 所示)。
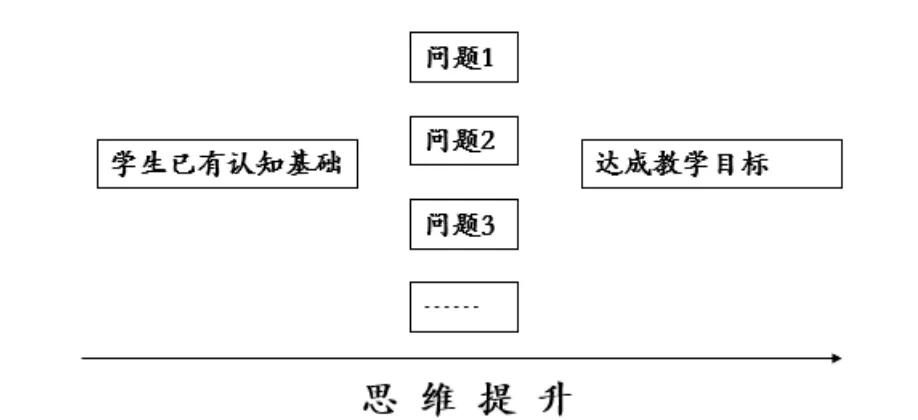
图2 平行式问题串教学,纵向提升思维
例如,笔者在教学“对称”时,对于寻找已知点的对称点,学生特别容易混淆。笔者分析原因是学生对知识点的熟练度不够,故而设计以下问题串:
问题1:分别求点(2,3)(-1,2)(-2,-2)(4,-1)(2,0)(-3,0)关于x 轴对称的点的坐标;你发现已知点和对称点之间有什么关系?
问题2:分别求点(2,3)(-1,2)(-2,-2)(4,-1)(2,0)(-3,0)关于y 轴对称的点的坐标;你发现已知点和对称点之间有什么关系?
问题3:点(2,3)(-1,2)(-2,-2)(4,-1)(2,0)(-3,0)关于x 轴、y 轴对称的点坐标分别是什么?你发现了什么?
解答以上三个问题时,教师要引导学生先画直角坐标系,正确标注已知点,然后数形结合找到对称点,接着对比已知点坐标和对称点坐标,发现坐标之间的关系,探究关系根源。只有在脑海中建立数与形的对应关系,才能从根本上理解“对称”。
课堂教学中,平行式问题串常常起强化和巩固作用。通过平行式问题串的解答,学生对所学知识更加熟悉,心理上产生亲切感,能够自然地接受知识并建构知识。“问题串”教学本质上是一种启发式、探究式教学,借助具有启发性的数学问题,让学生通过理解去掌握数学知识,推动学生数学思维发展。
(三)教学辐射式问题串,提升发散思维
辐射式问题串主要指,先设定一个主问题,由主问题向不同方向拓展分问题,形成辐射化的网状结构。辐射性问题串有助于学生多维度分析问题,更全面思考问题、解决问题(如图3 所示)。
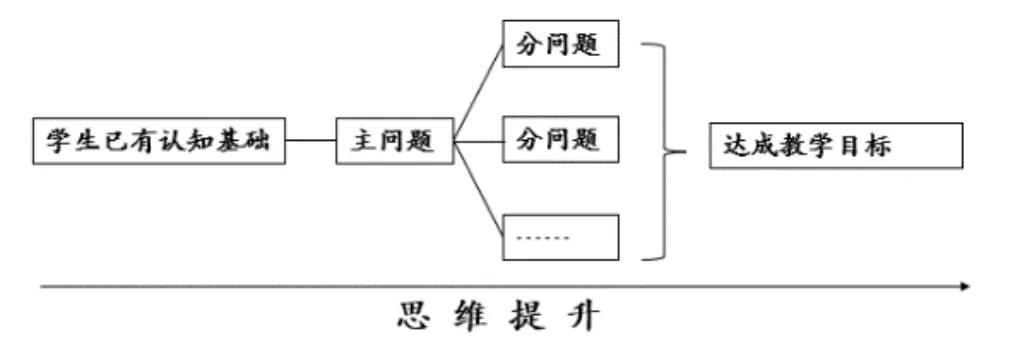
图3 辐射式问题串教学,提升发散思维
笔者在复习课教学时,经常设计辐射式问题串。例如,在复习“平行四边形”单元时,笔者设计的主问题是:平行四边的定义、图形和性质分别是什么?分问题是:长方形的定义、图形和性质分别是什么?正方形的定义、图形和性质分别是什么?学生通过问题串的解答,对平行四边形及其特例有了更清晰、更分明的认识。再如,复习“整式”时,主问题是:什么叫整式?分问题1:什么叫单项式,举例说明单项式如何运算?分问题2:什么叫多项式,举例说明多项式如何运算?指导学生分情况说理和计算,促使学生对整式、单项式、多项式的总分关系有了整体把握,对单项式和多项式的运算有了深入理解。
利用辐射式问题串,笔者尝试引导学生绘制知识导图,取得了不错的效果。一般主问题答案作为知识数的树干,分问题答案作为树枝,分问题的下级问题答案作为树桠。如,“函数”作为树干,“一次函数”“反比例函数”“二次函数”作为树枝,“表达式”“图像”“性质”等为树桠。初中阶段“函数”知识团整体回顾,能够有效提升学生类比、迁移思维。
三、指向思维提升的“问题串”的教学反思
1.“问题串”设计要具有针对性。针对性分两个方面。第一,问题目的要鲜明。为什么设计这个问题?设计这个问题是为了解决什么问题或达到什么目的?这就要求教师围绕目标设计问题,并准确地加以表述。第二,问题应立足学生基础。“问题串”的设计如果脱离学生现有知识、技能,脱离学生生活实际,那么必将无法有效促进学生温故知新,无法提高教学效率。
2.“问题串”要具有探究性。激发学生的思维是数学教学的核心,好的“问题串”应当能够激发学生的兴趣,实现学生的自主探索与合作交流,通过促使学生积极思考,使学生在“问题串”的引导下,通过自主探索实现未知向已知的转变。“问题串”过难,超过学生“最近发展区”,不可行;“问题串”过易,无实用价值。
3.“问题串”不是十全十美的。“问题串”固然能够驱动学生持续思考,但如果其中某一个问题出现了阻碍,那么学生的学习过程将会受阻难行。因此教师在“问题串”的设计与实施中必须规避这些不足,并且注意“问题串”教学时的生成性问题,合理使用具有激励性的评价语言,这样才能让“问题串”的作用发挥到最佳。

