混合保费收取下带有扰动双复合Poisson-Geometric过程的双险种风险模型

覃利华

混合保费收取下带有扰动双复合Poisson-Geometric过程的双险种风险模型

覃利华

（广西民族师范学院数理与电子信息工程学院，广西，崇左 532200）

考虑混合保费收取下有扰动的双复合 Poisson-Geometric 过程的双险种风险模型，对模型的性质进行讨论，证明盈利过程具有平稳独立增量和数字特征。运用概率和随机过程基本理论推导调节系数满足的方程，并得到破产概率的一般表达式和Lundberg不等式。当保费、理赔过程服从特定指数分布时，得到破产概率的具体表达式。

复合Poisson -Geometric过程；破产概率；Lundberg不等式；混合保费

0 引言

在经典风险模型中，理赔过程为单一险种的风险经营过程，也就是允许在充分小的时间内发生一次事故，并对同一险种进行多次赔付。但随着保险公司经营规模的不断扩大以及新险种的不断开发，用单一险种的风险模型来描述风险经营过程是有一定局限性的，根据这一要求，我们对复合 Poisson 模型进行推广，将单一险种推广为两险种，即考虑在充分小的时间内至多发生一次事故，并涉及到对两险种进行多次赔付的情况。此外，研究者们总是假设保险公司在单位时间内收到的保费是某一固定常数，但是在实际保险公司的业务中，可能跟一些投保人签订协议，在每个单位时间内投保人都会定期交固定的保费，但除此之外保险公司在单位时间内还会收到不同保费的保单，这是服从某一分布的随机变量。文献[1]将保费推广为服从某一离散分布的随机变量，建立随机保费的风险模型；文献[2-3]将双Poisson风险模型推广为带干扰保费混合收取的风险模型，并利用鞅的方法讨论了这种风险模型的破产问题。

在经典风险模型中，假设索赔过程是期望与方差相等的 Poisson过程，但保险公司往往会设置有免赔制度，即并不是任何索赔的发生保险公司都会赔付。因此，在这种情况考虑下的复合Poisson 风险模型就不符合实际情况。为了改进和优化该模型，文献[4]考虑索赔为Poisson-

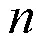
本研究考虑到随机干扰因素的影响，建立混合保费收取下带有随机干扰因素混合保费收取下复合Poisson-Geometric双风险模型，该模型在固定保费收取的情况上，考虑保费的随机化和险种的多元化，并且随机保费到达过程服从复合Poisson过程，理赔过程服从复合Poisson-Geometric过程。

1 模型的建立及介绍

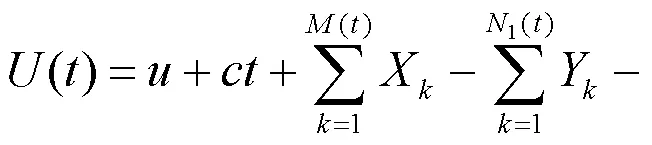
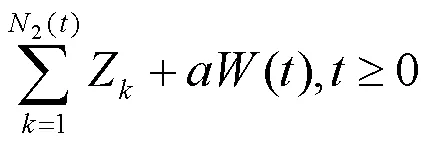
盈利过程为

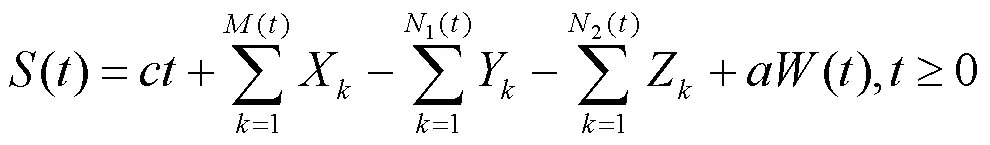
为了保证保险公司的正常运行，须保证收入总和大于支出总和，即

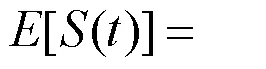
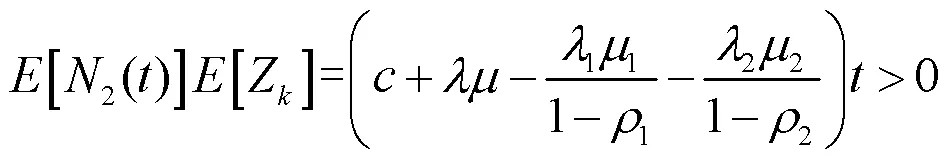
在此定义相对安全负荷系数为

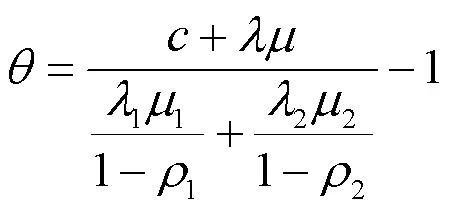
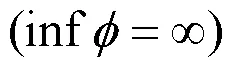
2 相关引理

1）具有平稳独立增量；

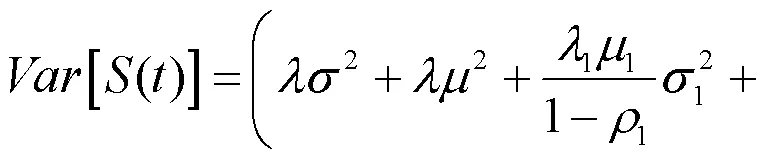
证明：

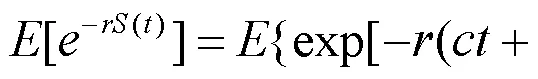
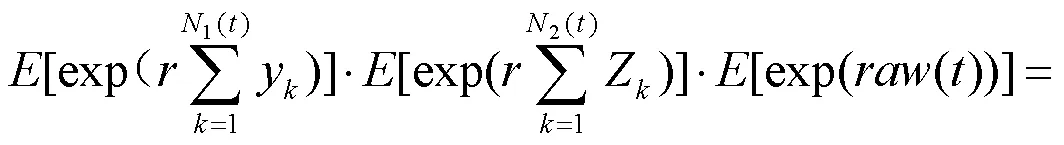
其中

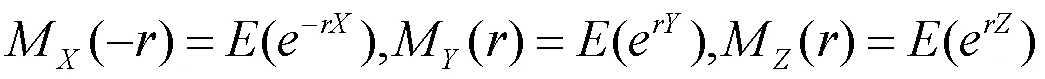
分别表示个体保单额、第一类理赔额、第二类理赔额的矩母函数，令

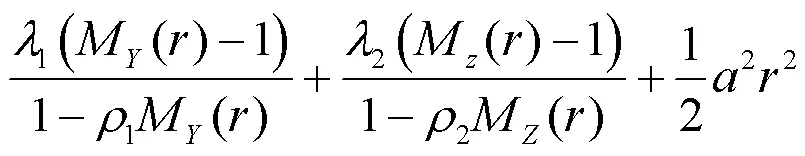
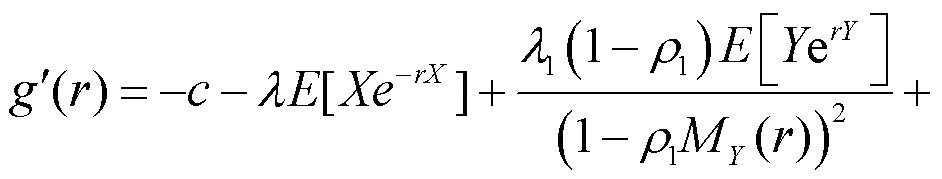
又因为

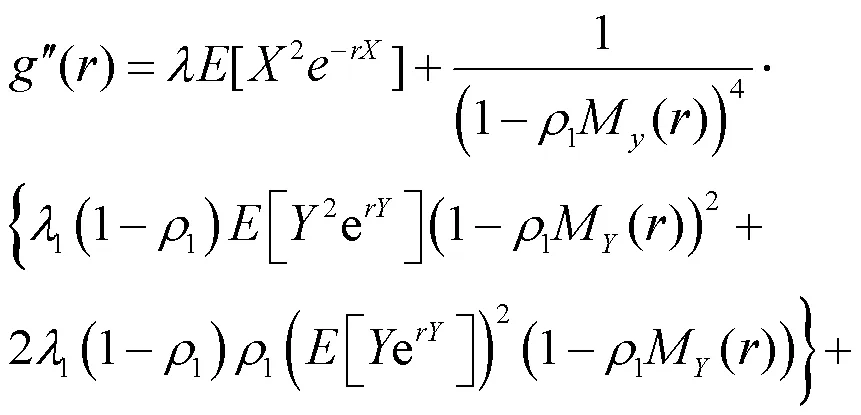
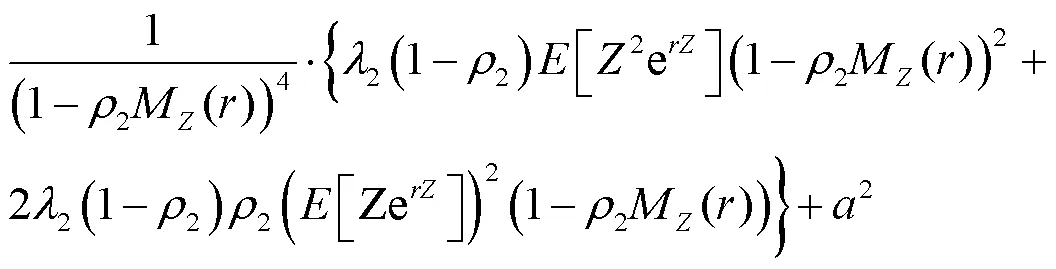
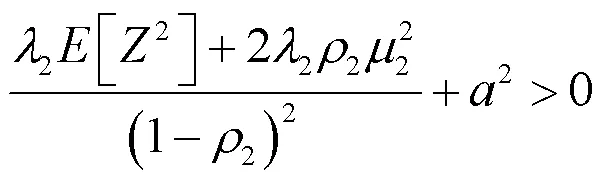
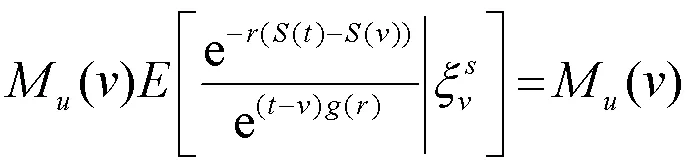
3 破产概率

定理1 风险模型（1）的最终破产概率满足Lundberg不等式：

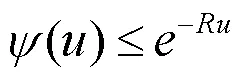
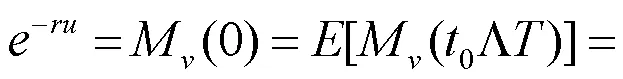
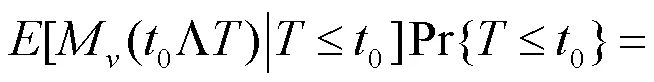
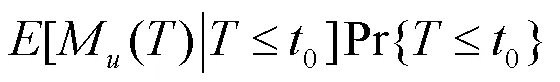
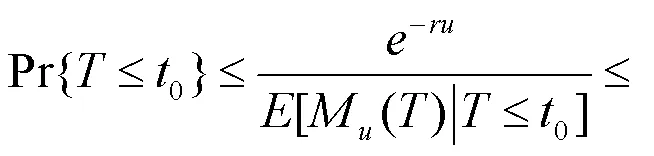
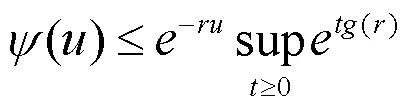
定理2 风险模型（1）的最终破产概率为

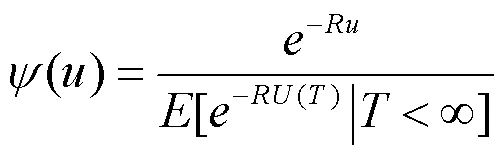
其中R为调节系数。

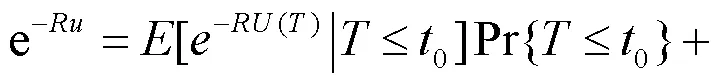
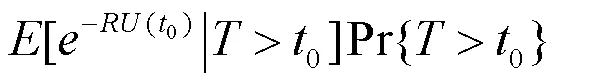
由控制收敛定理知

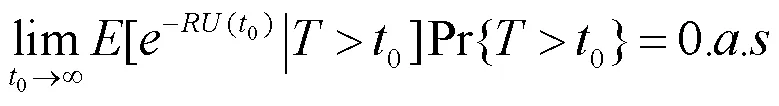
系数R的调节方程为

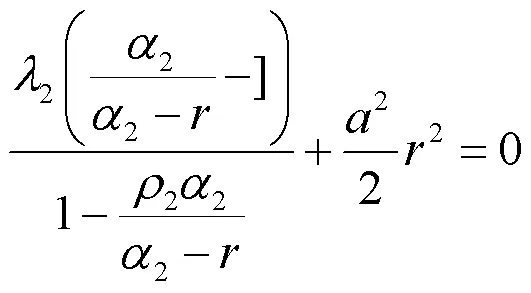
的正解。

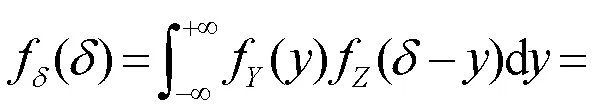
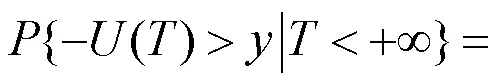
由此得到破产时财政赤字量的分布函数为

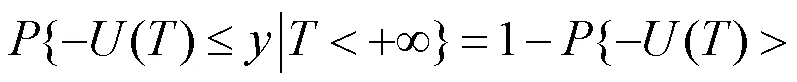
其概率密度函数为

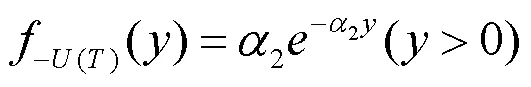
4 结语

本研究考虑到保险公司经营过程中会受到不确定随机干扰因素的影响和保费的随机化、险种的多元化，建立混合保费收取下带有随机干扰因素混合保费收取下复合Poisson-Geometric双风险模型，随机保费到达过程服从复合Poisson过程，理赔过程服从复合Poisson-Geometric过程。证明该模型盈利过程具有平稳独立增量数字特征。运用概率和随机过程基本理论推导调节系数满足的方程，并得到破产概率的一般表达式和Lundberg不等式。当保费、理赔过程服从特定指数分布时，得到破产概率的具体表达式。

[1] 毕秀春,张曙光.相依随机保费风险模型的有限时间破产概率[J].应用数学学报,2019,42(3):345-355.

[2] 覃利华.混合保费收取下带有随机干扰和支付红利的风险模型[J].数学理论与应用,2019,39(2):87-91.

[3] 刘冬元,廖基定,刘邵容,等.带干扰混合保费的多险种风险模型[J].南华大学学报:自然科学版,2013,27(4):53-55.

[4] 毛泽春,刘锦萼.索赔次数为复合Poisson-Geometric过程的风险模型及破产概率[J].应用数学学报,2005,28(3):419-428．

[5] 乔克林,李亚,徐佩佩．索赔次数为复合Poisson-Geometric过程的双险种风险模型[J].延安大学学报:自然科学版,2018,37(1):27-30．

[6] 刘美霞.考虑随机利率因素的双险种Poisson-Geometric过程模型的破产概率研究[J].科学技术与工程,2012,12(18):4321-4325.

[7] 王贵红,赵金娥,龙瑶．一类索赔为复合Poisson-Geometric过程双险种风险模型的破产概率[J].数学的实践与认识,2014,44(21):6-12.

[8] 孙宗岐,杨鹏.确定风险投资和有界分红下复合Poisson-Geometric风险模型研究[J]．西南师范大学学报:自然科学版,2020,45(7):1-10.

[9] 于文广,黄玉娟.干扰条件下复合Poisson-Geometric过程的多险种风险模型下的破产概率[J].山东大学学报:理学版,2008,43(2):16-18.

[10] 王月明,魏广华,郭楠,等.带借贷利率和干扰的双Poisson-Geometric风险过程模型[J].西南大学学报:自然科学版,2019,41(11):54-63.

[11] 韩建勤,乔克林.改进后的复合Poisson-Geometric风险模型的破产概率[J].延安大学学报:自然科学版,2016, 35(3):22-24.

[12] 小青.复合Poisson-Geometric过程的风险模型的破产概率及推广[J].统计与决策,2011(20):14-17.

[13] 高明美,孙浩,刘喜华.带干扰和投资的双二项风险模型的破产概率[J].统计与决策,2015(22):22-25.

THE PERTURBED DOUBLE-TYPE RISK MODEL UNDER MIXED PREMIUM INCOME OF DOUBLE POISSON-GEOMETRIC PROCESS

QIN Li-hua

（School of Mathematics, Physics and Electronic Information Engineering, Guangxi Normal University for Nationlities, Chongzuo, Guangxi 532200, China）

The perturbed double-type risk model under mixed premium income of double poisson-geometric process is taken into the consideration, and the properties of the model are discussed, the smooth independent increment and digital characteristics of the profit process are proved. By applying the basic theory of probability and random process, the equation satisfied with the adjustment coefficient, Lundberg inequality and the general expression of ruin probability are obtained. When the premium and claim processes obey the exponential distribution, the specific expressions of ruin probability are obtained.

compoundpoisson-geometric process; ruin probability; the Lundberg inequality; ixed premium

O211.6

A

10.3969/j.issn.1674-8085.2022.06.002

1674-8085（2022）06-0007-06

2022-02-22；

2022-04-07

广西高校中青年教师科研基础能力提升项目(2021KY0767）；广西民族师范学院科研经费项目(2021YB054）

覃利华(1987-)，女，广西来宾人，讲师，硕士，主要从事随机过程应用研究(E-mail:631898027@qq.com).