基于Swin-Transformer 的短波协议信号识别

朱政宇，陈鹏飞，王梓晅，巩克现，吴迪，王忠勇

（1.郑州大学电气与信息工程学院，河南 郑州 450001；2.郑州大学河南省智能网络和数据分析国际联合实验室，河南 郑州 450001；3.郑州大学电子材料与系统国际联合研究中心，河南 郑州 450001；4.信息工程大学数据与目标工程学院，河南 郑州 450001）

0 引言

短波通信凭借其设备简便、通信距离远等优点，广泛应用于多种通信场景中。为保证在不同通信系统下信息的有效传输，短波频段有种类繁多的通信协议[1]。由于短波信道存在多径衰落、多普勒频移以及人为干扰等特点，识别短波信号所属协议具有一定的难度。

目前，用于通信协议识别的传统算法主要分为基于特征提取的识别算法[2-3]和基于模板匹配的识别算法[4-6]。基于特征提取的识别算法通过对提取的信号特征进行分类实现信号协议识别，文献[2]使用调制识别中的熵距离参数分离频移键控（FSK,frequency shift keying）模式的110A[7]与STANAG4285[8]这2 种信号，但该算法仅适用于识别调制方式不同的信号；文献[3]通过识别信号中心频率、调制方式以及编码方式等属性形成信号特征向量，使用支持向量机对特征向量进行分类实现信号识别，但无法解决在低信噪比（SNR,signal to noise ratio）下信号特征难以提取的问题。文献[4]提出使用时域子序列匹配算法识别STANAG4285 等相移键控（PSK,phase shift keying）信号，并提出一种频域波峰匹配算法识别2GALE[9]等FSK 信号；文献[5]通过对待识别信号与构造的信号频谱模板进行相关运算，实现对未知短波协议信号的识别，但算法性能受频偏影响较大；文献[6]在频域模板匹配算法的基础上使用相位差分抑制频偏，对特定短波信号的识别具有较好的效果；但基于模板匹配的识别算法存在判决门限难以确定、对先验信息需求高等缺点。

近年来，随着深度学习的快速发展，神经网络算法广泛应用于信号处理领域，给通信信号识别技术带来了新思路。在信号调制识别领域，文献[10]使用原始同向正交信号作为输入，设计一维卷积神经网络（CNN,convolutional neural network），能够有效识别5 种调制方式信号。文献[11]关注调制信号的时频特性，使用时频图作为CNN 的输入，对多种信号取得了较好的识别效果。针对闭集识别存在易把干扰信号识别为有效信号的问题，文献[12]对神经网络中常用的Softmax 分类器加以改进，并采用改进的GE2E（generalized end-to-end）[13]损失函数，达到开集识别的效果。在短波信号识别领域，文献[14]使用信号时频图作为ConvNet 输入，对具有2、4、8 这3 种载波数以及窄、中、宽这3 种载波间隔的9 种模式进行区分，但所识别的信号模式有限；文献[15-16]利用特定信号在时频图上呈现的视觉特征，使用卷积神经网络对灰度时频图进行特征提取和映射，实现信号所属协议的识别，识别准确率与传统方法相比有明显提升。CNN 感受野大小对捕捉时频图中的特征差异有重要作用，文献[17]将ResNet[18]中的卷积核改进为扩张卷积核，在不增加参数量的情况下扩大感受野，进一步提升短波协议信号的识别率，但仍未解决CNN 中卷积层存在的感受野相对有限的问题。

Swin-Transformer[19]是一种基于自注意力机制[20]的神经网络模型，有对全局特征进行建模的能力，可以捕捉不同短波协议信号在时频图上呈现出的视觉特征差异。基于此，本文提出一种基于 Swin-Transformer 的短波信号协议识别算法。在多种复杂信道环境下，与CNN 识别算法相比，所提算法的信号识别准确率明显提升。本文具体研究工作如下。

1) 分析了短波协议信号在时频图上视觉特征的成因，建立一个用于训练神经网络的短波信号时频图数据集。数据集包含9 种常见的短波协议，为了模拟真实通信环境并提高数据多样性，在高斯白噪声环境下进行仿真，并对信号进行随机截断，模拟非合作通信无法确保从起始时刻接收信号的场景。

2) 研究了引入自注意力机制的Transformer 模型结构以及Swin-Transformer 的特点，并分析了Swin-Transformer 可以用于短波协议信号识别的原因。提出一种基于Swin-Transformer 的短波协议信号识别算法。

3) 仿真结果验证了所提算法的有效性。在短波多径时延、瑞利衰落以及强混叠的信道环境下，基于Swin-Transformer 的短波信号协议识别算法均具有较高的识别率。与现有算法相比，所提算法在识别率上明显提升。

1 特定短波信号的时频特性分析

不同短波通信协议规定的帧结构、调制方式、载波中心频率以及信号带宽等差异较大，而这些属性的差异导致信号在时频图呈现出不同的视觉特性。其中，CLOVER2000[21]是一种典型的采用多载波调制的短波协议，其采取了多种技术来适应短波复杂信道环境，在短波通信中有广泛应用；LINK11[22]作为一种活跃时间较长的短波协议，是LINK16 和LINK22 协议的研发基础，对后续协议的研究有重要参考意义。因此，本节以CLOVER2000 和LINK11 协议为例，对短波协议信号的时频特性做出具体分析。

时频分析结合时域和频域的特点，同时将信号的时间信息和频率信息展示在一幅时频图中，对时变非平稳信号的分析具有独特优势。常用的时频分析方法主要有短时傅里叶变换（STFT,short time Fourier transform）、Wigner-Ville 分布和小波变换等。STFT 由于计算量小、不存在交叉项等优点被广泛应用[23]，本文采取基于短时傅里叶变换的时频分析方法。

短时傅里叶变换的定义为

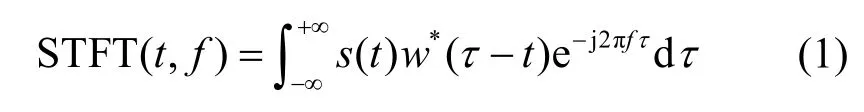
其中，t为时间，f为频率，s(t)为信号，w*(·) 为窗函数。

CLOVER2000 信号的波形由8 个音频并行组成，其中，最低频率为625 Hz，最高频率为2 375 Hz，相邻音频发送间隔为250 Hz。时域上，每个音频的发送时序按照音频序号从小到大间隔2 ms 依次发送。CLOVER2000 脉冲序号与频率的对应关系如表1 所示。

表1 CLOVER2000 脉冲序号与频率的对应关系

CLOVER2000 信号s(t)可以表示为

其中，P为信号的平均功率，ci,n为第i个音频的第n个码元，fi为第i个音频的频率，g(t)为成形脉冲，T s为脉冲持续时间，Δt=2 ms 为相邻音频的发送间隔。

对CLOVER2000 信号进行短时傅里叶变换得到其灰度时频图，如图1 所示。从图1 可以看出，CLOVER2000信号在时频上既呈现出了频域的8个音频，也体现出了每个音频发送时序不同的特点。

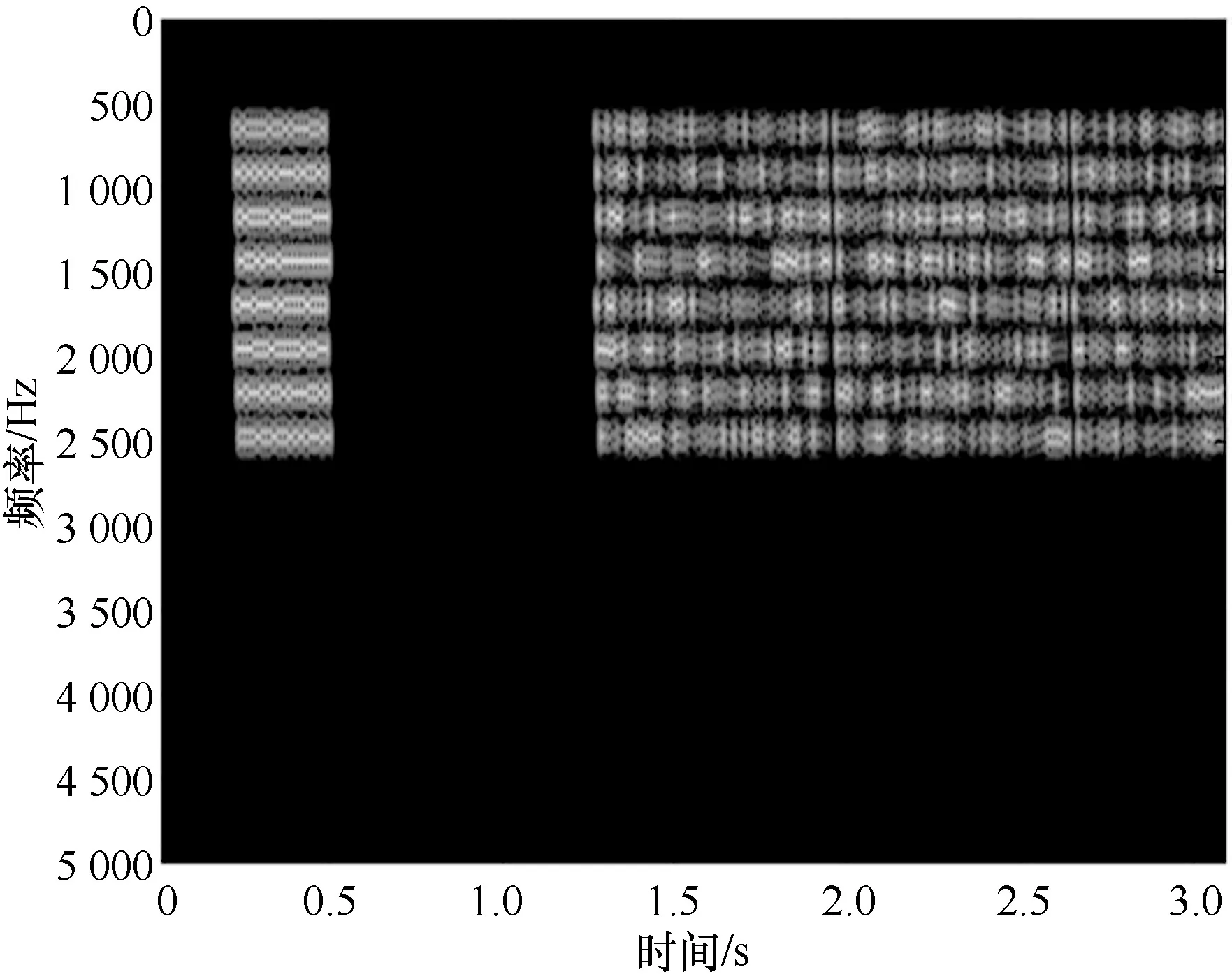
图1 CLOVER2000 信号灰度时频图

LINK11 信号共有6 种工作模式，本文以其中的网络控制站报告信号为例分析LINK11 的时频特性[22]，其帧结构如图2 所示。

图2 网络控制站报告信号帧结构

图2 中，同步序列由605 Hz 和2 915 Hz 音频组成，605 Hz 音频为多普勒校正音频，其功率比2 915 Hz 的同步音频大5～7 dB，此外，相邻帧的同步音频以π 进行相移，设初始相位为0，同步序列信号可表示为

其中，A1为多普勒校正音频幅度，A16为同步音频幅度，f1=605 Hz，f16=2 915 Hz。

位于同步序列之后的相位参考帧、起始码、信段以及终止码等均由16 个音频分量组成。除了605 Hz和2 915 Hz之外的14个音频频率位于935～2 365 Hz 之间，相邻音频频率间隔为110 Hz。多普勒校正音频不携带信息，采用四相移相键控（QPSK,quaternary phase shift keying）制方式，除多普勒校正音频外的15 个音频，每帧携带2 bit 信息，采用四相相对相移键控（QDPSK,differential QPSK）的调制方式。其信号可表示为

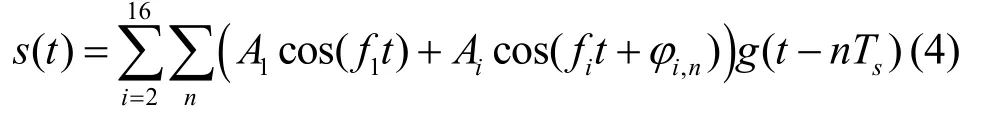
其中，Ai为第i个音频的幅度，φi,n为第n帧第i个音频的相位。图3 给出了LINK11 信号频谱。

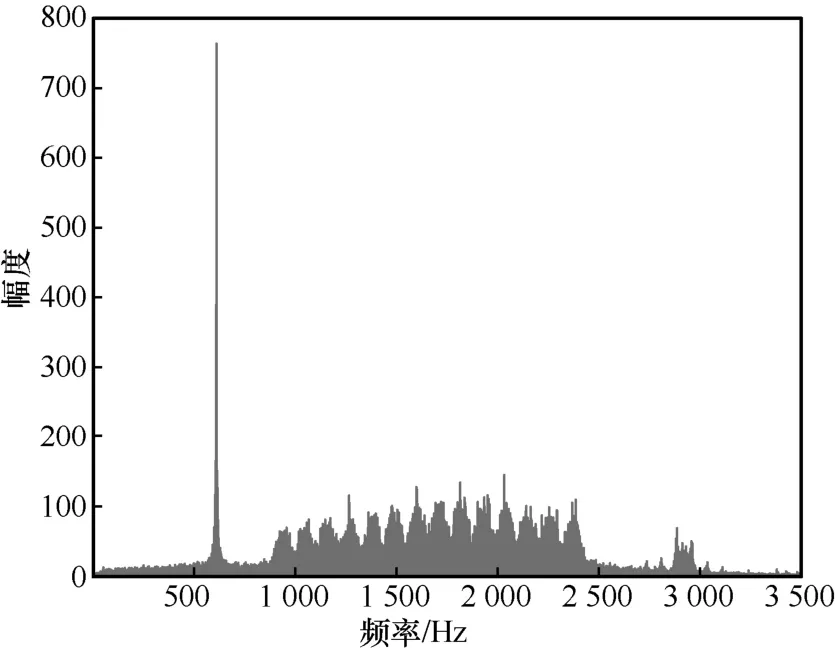
图3 LINK11 信号频谱

对整段LINK11 信号进行STFT，得到如图4所示的时频图。

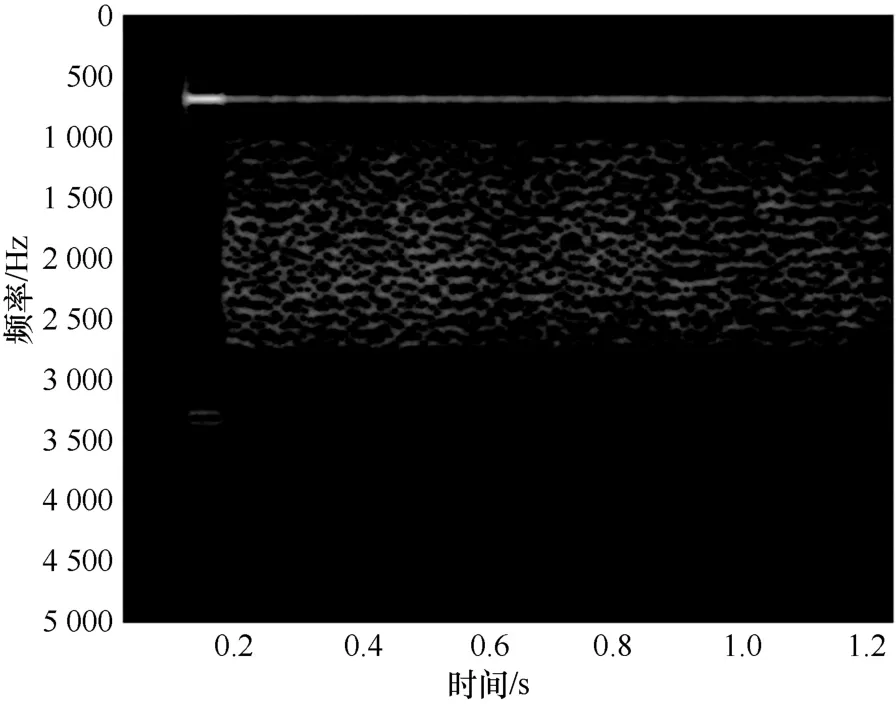
图4 LINK11 信号时频图

由图1 和图4 可知，CLOVER2000 和LINK11信号时频图呈现出截然不同的视觉特征，这是由于不同短波协议在制定过程中，对信号调制方式、传输模式以及帧结构等做出了不同设计。因此，通过对短波信号的时频进行视觉特征提取可以实现对不同短波协议信号的识别。

2 Swin-Transformer 网络模型结构

近年来，神经网络凭借其强大的特征提取能力在图像处理等领域取得了巨大成功，其中，Vaswani等[20]提出基于编码器解码器框架的Transformer 网络模型，该模型引入多头自注意力（MSA,multi-head self-attention）机制，具备学习全局特征的能力，其编码器结构如图5 所示。

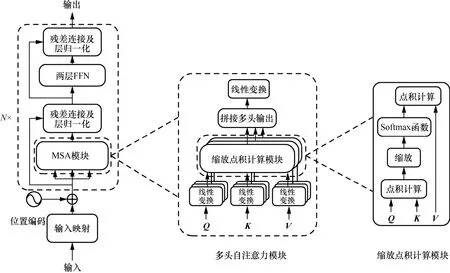
图5 编码器结构

假设输入序列长度为L，batch size 大小为B，则 Transformer 编码器的输入张量可以表示为M∈ℝB×L。M首先经过Input Embedding 映射成一个dx维的 Embedding，再与位置编码相加得到Transformer Block 的输入，这里的位置编码既可以采用正弦形式，也可以是通过学习得到的参数。每个Transformer 模块都由多头自注意力模块和两层的前馈网络（FFN,feed forward network）组成。其中MSA 和FFN 的输入、输出都采用残差连接的方式，输出还需要进行层归一化，整个Transformer Block 过程可以表示为

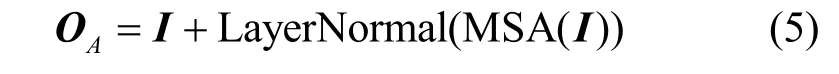
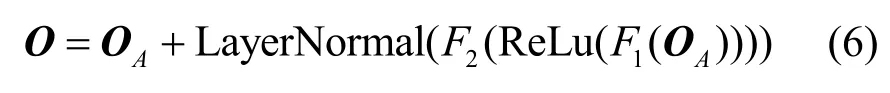
其中，OA为MSA 的输出，O为Transformer 模块的输出，F1(·)和F2(·)分别为前馈网络的第一层和第二层，其形式为F(x)=Wx+b。

假定MSA 有h个“头”，则每一个“头”的输出Ai定义为

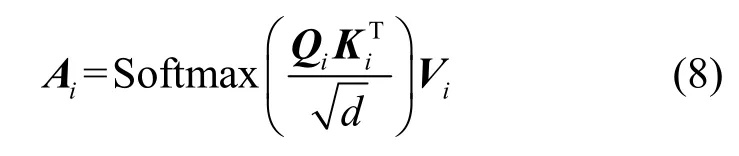
其中，Qi、Ki和Vi分别为

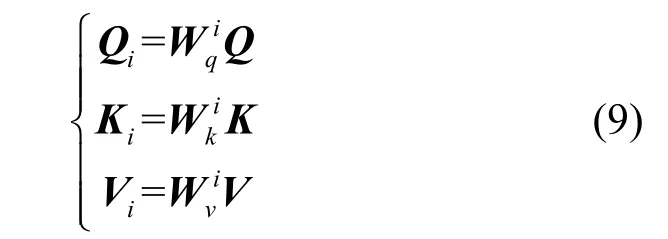
鉴于Transformer 在自然语言处理领域取得的成功，文献[24]提出Vision Transformer，将Transformer架构成功用于图像处理领域。具体地，首先将一个224 像素×224 像素大小的图像均分为196 个16 像素×16 像素大小的区域，其次将每个区域视为一个长度为256 的向量输入Transformer 编码器，并增加一个分类向量来表示全局特征，最后将分类向量经过Transformer编码器的输出用于Softmax进行分类。

Swin-Transformer 在Vision Transformer 的基础上引入CNN 中常用的层次化构建方式，在不同的层次对不同大小的窗口在内部进行MSA 操作，大幅降低了计算复杂度。同时通过滑动窗口操作增加窗口与窗口的信息交互，确保模型性能不会降低。具体来说，每一个Swin-Transformer 模块均采取与Transformer 编码器类似的架构，但与Transformer编码器不同的是，Swin-Transformer 模块将普通的MSA 改进为Window-MSA（W-MSA）以及Shift Window-MSA（SW-MSA）。SW-MSA 工作原理如图6 所示，本文采用的Swin-Transformer 网络模型具体结构如图7 所示。

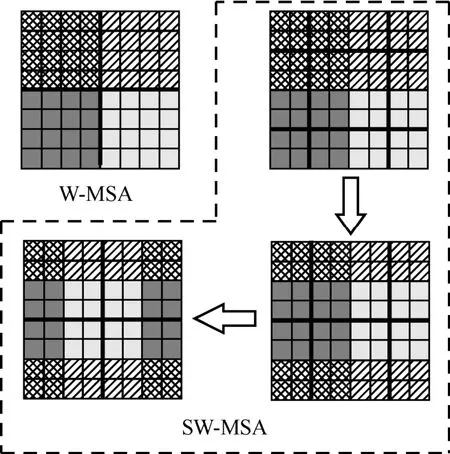
图6 SW-MSA 工作原理示意

图7 Swin-Transformer 网络模型具体结构

W-MSA 模块将输入特征图划分为多个窗口，在每个窗口内部进行MSA 操作从而大大减少了计算量。由于浅层网络的特征图尺寸相对较大，因此浅层的W-MSA 模块将特征图划分为更多的窗口，使每个窗口尽可能小，随着网络的加深，特征图划分的窗口相应减少。

为了使不同的窗口间进行信息交互，每个W-MSA 模块后面会紧接一个SW-MSA 模块。SW-MSA 模块首先对特征图重新划分窗口，其次根据特定的规则对窗口进行移位，对移位后的特征图进行窗口内的MSA 操作，此时的一个窗口内同时包含了多个移位前的其他窗口的特征，从而发挥出Transformer 长距离感知的优势。

Transformer 的全局感知能力对短波协议识别具有重要意义。CLOVER2000 与2GALE 时频图局部和整体对比如图8 所示。从图8 可以看出，调制方式为8FSK 的2GALE 信号的时频图与具有8 个音频的CLOVER2000 信号的时频图在局部具有类似的特征，但由于二者帧结构、带宽以及中心频率等存在差异，因此可以凭借全局特征对2 种信号进行分辨。综上，对图像具有长距离感知能力的Swin-Transformer可以通过对信号在时频图上呈现出的视觉特性进行特征提取，从而实现对短波信号的协议识别。

图8 CLOVER2000 与2GALE 时频图局部和整体对比

3 仿真测试与分析

短波协议数量众多，短波协议识别暂时没有一个公开的标准数据集，因此，本文从目前常见的短波协议中选取了具有一定代表性的110A、110B[25]、2GALE、3GALE[26]、CLOVER2000、CIS-45、LINK11、PRC4+4 和STANAG4285 这9 种短波协议信号的时频图制作数据集。其中，CLOVER2000和LINK11 前文已有介绍；2GALE、3GALE 分别为短波第二代、第三代自动链路建立协议，分别使用FSK 和PSK 波形对信道进行探测实现信道评估；110A、110B、STANAG4285 为短波通信军用标准，采用了多种纠错编码、交织、加扰等技术，并且信号按照严格的帧结构进行发送，包含了多数短波协议的特点；CIS-45 及PRC4+4 分别为典型的采用OFDM 和多载波调制的短波协议，而正交频分复用（OFDM,orthogonal frequency division multiplexing）和多载波调制是短波协议使用较多的调制模式。综上，9 种信号的调制模式包含多种短波信号常用的调制模式，在短波协议中具有一定代表性。因此，本文选择这9 种短波协议信号制作数据集，通过对这9 种信号的识别，可以说明本文算法对多种类型的短波协议信号识别具有一定的普适性。此外，为了增加数据集的可靠性和多样性，对仿真信号及数据集做以下处理。

1) 短波信道环境恶劣，信号受噪声影响严重。本文采用高斯白噪声，且SNR 范围为-10～10 dB。

2) 在非合作通信场景下，接收方无法确保接收信号的完整性，同时考虑到实时识别的要求，信号的长度不宜过长，因此对仿真信号随机截取时长为0.5～5 s 的子序列。

3) 考虑到闭集识别的局限性，本文使用9 种信号之外的部分短波信号以及调制方式为PSK、FSK的普通信号组成单独的噪声类，来提高算法对数据集中9 种信号之外的其他部分短波信号的区分能力。

基于以上3 种处理措施，训练集样本由每类信号产生500 个灰度时频图样本得到，每个样本大小压缩为224 像素×224 像素。数据集中9 种短波协议信号的时频图如图9 所示。从图9 中可以看出，由于不同信号在帧结构、带宽、中心频率及调制模式等方面存在差异，各信号在时频图上呈现出不同的视觉特性。

图9 数据集中的9 种短波协议信号时频图

本文仿真实验环境的硬件与软件配置信息如表2 所示。训练过程的学习率设为0.000 1，batch size设置为32，epoch 最大设为20，采用AdamW 优化器。

表2 仿真实验环境配置信息

图10 给出了所提算法在高斯信道下对9 种信号的识别率，每种信号在各信噪比下的样本数为500。从图10 可以看出，低信噪比下各信号识别率差异较大，但当SNR＞-4 dB 时，9 种信号的识别率均已接近100%，说明所提算法能够对9 种信号进行有效识别。

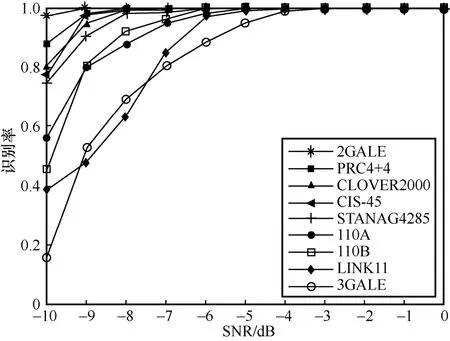
图10 所提算法在高斯信道下对9 种信号的识别率

理论上，基于Swin-Transformer 和基于ResNet的神经网络算法均能够通过增加网络深度实现性能的有限提升，但网络层数的增加会导致算法计算量增加以及过拟合风险加大，因此本文选择了与所提算法计算量接近的ResNet50 和ResNeXt50[27]这2 种CNN算法。此外，在非神经网络算法中，时域模板匹配算法作为一种通用的短波协议信号识别算法，事先对待识别协议信号建立模板库，通过计算待识别信号与模板信号的相关系数来确定信号所属类别。图11 给出了高斯信道下4 种算法的性能对比。

由图11 可知，神经网络算法凭借强大的特征提取能力，其对短波协议信号的识别性能要优于传统的时域模板匹配算法，且神经网络算法在识别过程中不需要将待识别信号与信号库一一对比，识别流程相对更直接。此外，由于Swin-Transformer 引入了全局感知能力更强的自注意力机制，相比于传统的CNN 具有更大的感受野，而短波协议间的差异在时频图呈现出的视觉特性差异同样是全局性的，因此Swin-Transformer 算法在短波协议识别上比感受野相对有限的CNN 性能更好。

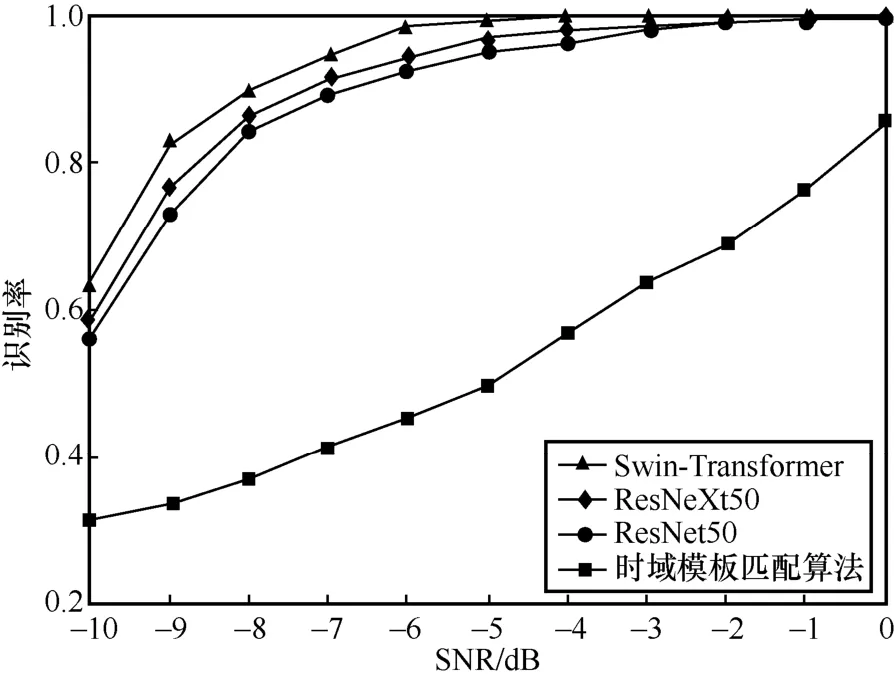
图11 高斯信道下4 种算法的性能对比

另外，短波频段频谱资源紧张，实际接收到信号可能存在叠加干扰，因此需验证所提算法对存在干扰的信号识别性能。本文使用的干扰信号调制方式为8PSK，带宽为f1，被混叠信号带宽为f2，两者重叠带宽为f12，2个信号在时间上完全重叠，文献[16]对频域上干扰混叠度D的定义为

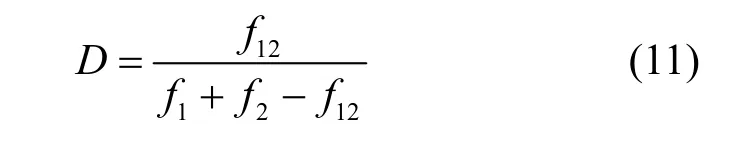
在存在叠加干扰的情形下，此时用信号干扰比（SIR,signal to interfere ratio）表示信号与干扰功率之比，单位为dB。图12 给出了干扰混叠度及干扰信号功率对所提算法识别性能的影响。从图12 中可以看出，在干扰信号功率较大（SIR=0）且时频混叠程度较大的情况下（D=0.5 或D=0.7），本文所提算法性能受影响较大，因为此时信号在时频图上呈现的视觉特征大部分被干扰信号所遮挡，所提算法无法提取出有效特征进行识别。但当SIR>10 dB，即信号功率明显大于干扰功率时，本文所提算法对4 种混叠程度下的短波协议信号均有超过90%的识别率，说明所提算法具有较好的抗干扰能力。

图12 叠加干扰信号下所提算法识别率

此外，Watterson 信道模型是一种经典的短波信道模型，本文采用文献[28]建议的信道参数。图13给出了所提算法在Watterson 信道下算法的识别性能。由图13 可知，在Watterson 信道下，当SNR＞13 dB 时，本文所提算法在8 种信道条件下的识别率均接近100%。

图13 Watterson 信道下所提算法识别率

4 结束语

本文针对传统短波协议信号识别算法低信噪比下识别率低、识别信号单一以及对先验信息需求高等问题，研究了短波协议信号在时频图上视觉特征的原因，提出一种基于Swin-Transformer 的神经网络短波协议信号识别算法，通过对信号的灰度时频图进行特征提取并映射实现对信号所属协议的识别。实验结果表明，基于Swin-Transformer 的短波协议信号识别算法在高斯白噪声信道、存在强混叠信号和Watterson 信道环境下均具有较高的识别率。