动力定位船舶推力分配问题研究*

曹宇翾 杨宣访 李厚朴

（海军工程大学电气工程学院 武汉 430033）

1 引言

随着人们对海洋资源的勘探及开采不断深入，海洋深度也逐步增加，很多海上作业对于船舶的定位精度有着越来越高的要求。传统的锚泊定位方式由于受到远海水深和精度要求等相关因素的限制，已经不能满足船舶作业的要求，海洋装备的发展使得动力定位系统（Dynamic Positioning System，DPS）诞生并成为了许多海上作业船舶不可或缺的重要支撑，很好地解决了这一实际问题［1］。

国际海事组织（International Maritime Organization，IMO）定义，DPS表示动力定位船舶需要装备的全部设备，包括动力系统、推进系统、动力定位控制系统［2］；中国船级社（China Classification Society，CCS）的船级规范定义，DPS表示使动力定位船舶实现动力定位所必需的一整套系统，包括动力系统、推进器系统、动力定位控制系统和测量系统［3］。

DPS是一个复杂的闭环控制系统，利用自身配置的传感器检测出船舶当前所处的实际位置以及当前所受外界海洋环境的影响程度，运用上层控制系统中的控制算法得出船舶达到预定位置所需推力和扭矩，与前馈环境补偿相加，作为推进系统的输入指令；推力分配单元接受到指令后，根据推进器布置规则，结合推力损失分析，选择适当的分配算法分配对各个推进器相应的推力和扭矩，使其尽可能保持在作业要求的位置。

本文主要研究DPS中推进系统的推力分配环节，针对新型动力定位船舶，其性能直接影响动力定位船舶的控制能力。推进器的增加无疑提高了船舶的可操纵性以及控制系统的可靠性，但同时也增加了推力分配管理的难度和推力分配方法的多样。所以，在对动力定位船舶推力分配进行研究时，推进器的合理布置及推力的损失分析、优化分配算法和分配策略等成为了十分重要的研究课题。

图1 船舶动力定位系统工作原理图

2 推力系统推进器研究

2.1 推进器种类及布置规则

在DPS的推进系统中，推进器产生推力和方位角控制船舶位置和艏向，动力定位船舶常用的推进器类型主包括固定方位推进器和全回转推进器等。固定方位推进器主要有主推进器和槽道推进器两种类型，推进器方向固定不变，推力范围限定在一个线形区域，分别抵抗船舶所受的纵向外载荷和横向外载荷。全回转推进器能绕竖直轴360°进行旋转，产生水平面任意方向的推力，对于经常需要调节推力大小和方位的DPS来说非常适用，是使用最普遍的推进装置。

CCS2002年发布的《海洋工程动力定位系统检验指南》中对推进器布置提出了通用规则［3］，要求推进器位置应尽量减少推进器与船体之间及推进器之间的干扰，在规定环境下推进器系统应提供动力定位船舶足够的力和力矩。基于此，在不考虑冗余和功耗等问题时，有三种最小规模的推进器布置实现，能控制船舶的纵荡、横荡和艏摇。

图2 最小推进器布置图

第一种实现：两个槽道推进器和一个螺旋桨推进器，布置分配方程为

纵轴方向力：Fx=T3

横轴方向力：Fy=T1+T2

回转力矩：Mz=T1L1-T2L2

第二种实现：1个槽道推进器和1个全回转推进器，布置分配方程为

纵轴方向力：Fx=T2cosϕ2

横轴方向力：Fy=T1+T2sinϕ2

回转力矩：Mz=T1L1-T2L2sinϕ2

第三种实现：两个全回转推进器，布置分配方程为

纵轴方向力：Fx=T1cosϕ1+T2cosϕ2

横轴方向力：Fy=T1sinϕ1+T2sinϕ2

回转力矩：Mz=T1L1sinϕ1-T2L2sinϕ2

2.2 推进器推力损失成因

推进器在水下根据指令改变推力和方位角时，变化的水流形成复杂流场，与海浪和海流发生相互作用，导致海流对推进器、推进器与船体及推进器之间产生干扰，产生的实际推力小于在敞水试验中得到的理论值，水动力性能降低［4］。在进行作业时，动力定位船舶一般处于低速状态，相较于推进器之间干扰对推力产生的影响，海流和船体运动对推进器的影响相对较小，可以在研究中忽略不计，因此在分析推进器推力损失成因时，主要考虑相邻推进器之间产生的相互干扰［5］。

相邻推进器之间相互干扰的主要原因是上游推进器工作时产生的尾流会影响下游推进器，导致下游推进器的进水口水流速度增加，推力系数明显下降，产生的推力和扭矩随之变小［6］。国内外已有许多学者对推进器之间干扰问题进行研究，主要手段包括模型试验和CFD数值模拟，发现推进器之间的干扰主要取决于推进器间的距离及桨轴之间的夹角。Lehn等［7］的研究表明，两个推进器间距越小，下游推进器的推力损失越严重。Dang等［8］通过平板模拟船体，估算出受船体影响时下游推进器推力利用率的经验公式：

Lehn等［7］在敞水中对两个推进器进行前后布置时，同时发现桨轴线之间的夹角会对下游推进器的推进效率产生较大影响，Dang［8］根据实验估算得出了经验公式：

式中，φ表示两推进器桨轴线之间的夹角，t表示夹角为0时的推力利用率，tφ表示夹角为φ时推力利用率。

此外，李博等［9］对推进器转速对下游推进器效率的影响进行了实验，结果表明上游推进器的转速越高，对下游推进器的效率影响越大，其效率也越低，反之当上游推进器的转速较低时，对下游推进器的干扰较小。

2.3 推力损失处理策略

推进系统中在进行推力分配的过程中，推进器之间产生的干扰问题虽然无法完全避免，但可以采取一些有效的方法策略来尽量降低干扰产生的影响，提高推进器运转效率。

目前主要的思想有三点，一是直接设置固定禁区角，对全回转推进器设置禁区角，避免推进器在禁区角发力；二是限制禁区角内的推力上限，当推进器进入禁止域时，可以通过降低上游推进器的转速，限制推进器的最大推力，减少对下游推进器的干扰作用；三是设置动态禁区角，全回转推进器的禁区角范围随着相邻推进器间的相对转速变而进行实时调整，最大限度利用推进器推力，提高推进器效率［9］。

3 推力分配算法研究

3.1 推力分配问题描述

动力定位船舶为了始终稳定在海平面上预定的位置，会装备比常规船舶更多种类和数量的推进器。DPS中推进器的数目一般多于五台，意味着对于一组给定的控制力，系统存在很多种不同推力大小和方向的组合。推力分配要解决的问题就是实时进行推力分配，在众多组合中找到最优分配方案［10］。

动力定位控制器通过状态反馈η和v计算船舶达到预定位置所需的推力和扭矩τc，推力分配单元负责将τc转化为各推进器的控制输入α和u，满足如下关系［11］：

式中，τc∈R3和T∈Rr表示推进器推力，α∈Rp和u∈Rr表示控制输入，具体为：

推力系数矩阵K∈Rr×r为对角阵，表示为

B(α)∈R3×r为推进器布置矩阵，可表示为 r 个列向量bi∈R3的形式：

每一台推进器对应一个列向量，动力定位船舶三自由度运动控制下，不同类型推进器对应b的表示为

主推：bi=[1,0,lyi]T

侧推：bi=[0,1,lxi]T

全回转推进器：

式中，(lxi,lyi)表示第i个推进器在船体坐标系的位置；X为纵轴方向，艏向为正；Y为横轴方向，右舷为正。

推力分配问题中在建立目标函数时，一般会考虑的因素有能耗、误差及推进器方位变化率等。综合各方面因素考虑，目前相关研究中考虑因素最多的目标函数为

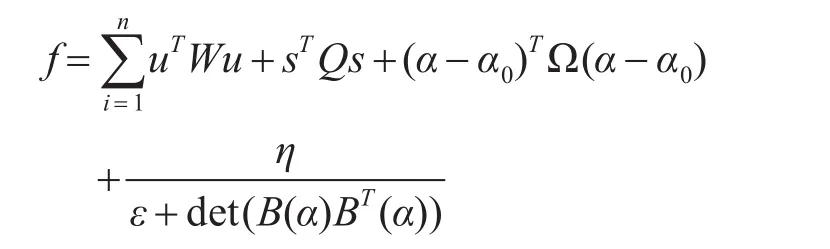
式中，第一项为消耗的总功率；第二项为惩罚项，用来控制要求推力和实际分配推力之间的误差s，Q为正定对角矩阵；第三项为限定全回转推进器方位频繁变化，减少磨损；Ω为正定对角矩阵；第四项用来避免奇异结构。

3.2 推力分配优化算法

DPS的推力分配问题根据实际情况的需要，一般会适当忽略部分考虑因素，对上述目标函数进行简化，将问题分为线性无约束分配、线性约束分配和非线性约束分配三大类［12］。针对不同类型的分配问题，相应的优化算法得到广泛的应用，常用的推力优化分配算法有广义逆法、序列二次规划算法、粒子群优化算法等。

广义逆法是广义控制分配中比较常用的算法，其基本思路为仅考虑能耗最低，将上述目标函数仅保留功率消耗项，利用推力误差等式作为限制条件，设计Lagrange函数求解目标函数极值。该算法的优点是方法简单、直接，但在计算过程中可能出现奇异结构，使得解过大而不能应用实际。国内外学者针对算法的缺点对该算法进行了改进，Sørdalen［13］将奇异值分解法引入到推力分配问题广义逆法求解，对推力结构矩阵进行奇异值分解，避免产生奇异结构；徐海祥等［14］针对全回转推进器在进行推力分配时，可能因物理限制存在推力饱和或角度饱和的问题，采用级联广义逆算法，对饱和的推力和角度进行截断处理，保证满足上层控制器的要求。

对于推力分配这类非线性约束问题，序列二次规划（SQP）算法是间接求解该类问题比较有效的手段，由美国数学家Wilson在1963年提出［15］，具有收敛速度快、简单易行等优点，但过分依赖于初始值，存在局部收敛等问题。其基本原理是把推力分配优化问题离散近似成一组等效的凸规划序列，利用Lagrange-Newton法形成迭代关系，最后求得最优解。吴显法等［16］以深海钻井和采油平台为研究对象，采用SQP算法达到降低能耗的目的，避免了奇异结构，提高了系统操纵性；刘鹏等［17］对挖泥船自身配置的推进器系统进行分析，运用SQP算法满足了挖泥船的定位要求。

粒子群优化算法由于需要调节的参数非常少，对算法参数调整比较容易，已被应用到很多领域。该算法是对鸟群寻找食物的行为进行模拟，将寻找最优解的过程比作鸟群寻找食物的过程，在这个过程中，每只鸟都有记忆功能，会记录自身曾经找到的历史最优位置并共享给整个鸟群，对整个鸟群最佳鸟的位置信息和速度信息进行更新，直至迭代结束。该算法的原理比较简单，导致了存在求解精度不高、在规定迭代次数达不到理想收敛精度的问题。尚留宾等［18］针对粒子群优化算法解决动力定位推力分配问题此类易遭遇局部最优、计算时间长等瓶颈，探索不同粒子决策变量对推力分配结果的影响，构建了基于3种不同粒子决策变量的粒子群推力分配算法，提高了推力分配的实时性；李新想等［19］提出了一种以粒子群算法为基础，引入混沌理论和遗传算法中交叉变异策略的混合算法，通过对某铺管船的仿真，证明该算法在兼顾能耗的同时有效降低推进器磨损。

除上述算法外，部分文献资料针对上述算法应用在推力分问题中存在的不足，将算法进行了结合和改进，如多智能体粒子群优化算法、粒子群优化算法与SQP算法相结合等；还引入了其他算法，如遗传算法、偏置推力分配算法等。

4 推力分配策略研究

4.1 推力分配模式

动力定位船舶在处于不同作业模式或海洋环境是，推力分配模块需要解决的主要问题不同，单一的分配方法可能会导致分配时间过长，无法有效地解决各种推力分配问题。制定多种分配模式在相应的工况和环境下互相切换，有利于降低能耗和机械磨损，提高DPS的稳定性。对于广泛配置全回转推进器的动力定位船舶来说，一般分为固定角度模式、可变角度模式等。

固定角度分配模式适用于海洋环境平稳、控制系统产生的控制力较小但方向多变的情况，能降低推进器因控制力方向频繁变化的磨损。该模式在运行前，要根据当前可用的推进器数量和推进器之间的相互干扰，预设多组方位角；切换至该模式，系统根据环境力方向从中选择最佳方位角［20］。固定角度分配模式通常采用广义逆法求解，文献［21］也证明在环境载荷较小但方向可能不断变化的海况下，广义逆法有效解决了该模式下的推力分配问题。

可变角度分配模式适用于海洋环境力较大且方向较为稳定的情况。该工作模式下，系统自动改变全回转推进器的推力和方位角，产生船舶达到预定位置所需的推力和力矩，使其总是保持能耗最小。求解可变角度分配模式下的推力分配问题时，一般采用SQP等迭代算法，同时为避免推进器连续转动，还可以对推进器设置角度死区，在一个控制周期内，若推进器转过的角度小于阈值时，推进器方位角不改变［22］。

4.2 分配模式切换

推力分配模块中需要设置各种有效的切换指标保证各种模式面对不同的工况和环境能任意切换，切换指标需要对各种可能的推力组合要求作充分的考虑，保证切换的有效性。Swanson［23］在研究时将海况分为平静海况和恶劣海况，用能耗大小作为平静海况下固定角度模式和恶劣海况下可变角度模式之间切换的参考量；Ruth［24］提出迟滞切换的概念，以待分配力和力矩的特性作为参考，对上层控制系统的输出指令进行低通滤波，将所得滤波值作为切换指标，减少推进器频繁切换；王芳［25］考虑能耗函数、误差函数以及响应时间，将多项性能加权作为切换函数，将该函数与选定阈值作比较来确定环境力的大小，以此作为切换指标；周兴［26］以控制力、能耗项作为对应海况的切换指标，以当前位置与期望位置的差值作为工况的切换指标，建立了分级处理的切换机制。

图3 分配模式切换机制示意图

5 推力分配研究方法趋势展望

动力定位船舶在探索深远海域的作用不断凸显，对于DPS稳定性、鲁棒性及定位能力等要求也不断提高，相关学者不断将一些新的理念引入DPS，推力分配问题相关研究得到了较大发展，主要趋势体现在以下几个方面。

1）深入分析推力损失

目前避免推力损失采取的策略大都是直接设置固定禁区角与限制禁区角内推力上限相结合的方式，在设置固定禁区角的同时，允许分配最优解在禁区角范围内并限制最大推力，但当方位角长时间处于禁区时，强制改变至禁区边界。从运用机理来讲，第三种思想设置动态禁区角最大限度利用全回转推进器，相比该策略较大增加了推进器效率。但是推进器之间的干扰因素相互影响，当禁区角范围随着相邻推进器间的转速比进行调整时，干扰因素相互耦合，很难对推进器转速与禁区角的关系进行定量分析。所以，研究确定两者明确的数学关系，可以使分配的推力和力矩指令避免二次处理，是避免推力损失减少能耗下一步研究的关键。

2）深入应用人工智能

人工智能技术在动力定位船舶推力分配研究中的应用正处于起步阶段，相关学者已经进行了相关研究。衣凡等［27］将神经网络引入推力分配研究，利用BP神经网络拟合推力损失函数，将推力损失加入到推力分配的数学模型中，取消了禁止角；徐海祥等［28］提出了一种基于极限学习机（ELM）的推力分配方法，提出了一种基于ELM的推力分配方法，并进行了离线和在线仿真实验，结果表明了该方法求解精度与SQP算法相当，但求解时间大大缩短，实时性的大幅度提高。所以，人工智能在动力定位船舶推力分配问题求解中的应用是行之有效的，前景十分广阔，值得进行深入研究。

6 结语

本文结合国内外研究现状，主要对DPS中推力分配环节中推进器的合理布置及推力的损失分析、优化分配算法和分配策略进行研究分析。推力分配问题求解在推进器之间相互干扰、控制因素冗余、复杂海洋环境等因素影响下，随着“科技兴海”战略的持续推进，动力定位船舶的推力分配研究发展越来越深入，很多难题瓶颈得到解决，继续在开发海洋资源方面发挥更大更好的作用。