基于电警数据的单点自适应信号控制优化方法

骆旅舟，谈超鹏，唐克双

（1.同济大学交通运输工程学院，上海 201804；2.同济大学道路与交通工程教育部重点实验室，上海 201804）

交通信号控制是城市道路交叉口的重要交通管控手段之一，主要包括定时、感应和自适应等控制方式。其中，单点自适应信号控制可以根据检测器信息对交叉口未来交通运行状况进行预测，并基于优化模型实时生成最佳的信号配时方案，可以较好地适应交通流的随机时变特征，被认为是最有效的信号控制方式之一［1］。

现有的单点自适应信号控制方法主要依赖以线圈为代表的传统定点检测器和以网联车为代表的移动检测器。前者通常布设在停车线附近［2］、停车线上游［3-4］或上游交叉口［5-6］，由于其技术发展成熟，因此在现有自适应信号控制方法中应用最为广泛。经典的SCATS［2］与SCOOT［6］系统分别对交叉口交通状况进行模式匹配或者实时预测，然后通过动态方案选择或者实时方案生成的方式优化信号控制参数。与SCOOT系统类似，Larry［5］根据上游交叉口的信号配时、排队和路段自由流速度等信息预测下游的车辆到达。Sen和Head［7］在其基础上，提出相位受控优化模型（Controlled Optimization of Phases，COP），使用动态规划求解每个相位的最优时长。Chen 和Sun［4］进一步考虑车辆在下游红灯或绿灯到达的两种情况，对车辆的排队过程进行了建模，同时将NEMA相位结构应用于COP模型。Cai等［3］采用5s与0.5s两种时间粒度预测未来10s的短时车辆到达，提出了基于近似动态规划的自适应控制算法，结果表明增大配时方案的更新频率能够显著改善控制效益。

尽管线圈能够采集流量、速度和占有率等交通参数，但由于不能获取车辆身份信息，在交叉口多车道场景下难以获取个体车辆的行程时间，因此少有相关研究考虑车队的离散。以网联车为代表的移动检测器则能够提供更加精细的交通数据，强化系统对交通流变化的感知。考虑到现实中较低的渗透率，Feng 等［8］采用车辆位置与速度估计算法得到未联网车辆的状态信息，将路段划分为自由流区、减速区和排队区，从而预测交叉口的车辆到达；随后使用改进后的COP模型，采用基于动态规划的双层优化算法进行求解。Cai等［9］不直接预测车辆的到达，在车路协同环境下预测车辆的行程时间，建立了以车辆行程时间最小为目标的优化模型。同样地，Lee等［10］利用卡尔曼滤波估计累计行程时间，进而决定延长当前相位或切换到下一个相位，但是验证结果表明该算法仅在渗透率大于30%的情况下有效。由此可见，目前较低的渗透率和上传频率仍然是制约网联车数据应用的重要因素。

电子警察（简称电警）系统可以实时采集车辆通过交叉口停车线的时间、所在车道及其身份信息，近年来在我国城市道路交通管理中被广泛应用于交通违章执法。相较于线圈等传统定点检测器，电警具有数据质量高、覆盖范围广、车道级全样本检测的特点。同时，通过上下游电警数据的车辆号牌匹配，还可进一步得到车辆路径及其行程时间。在交通状态估计方面，电警数据具有巨大的挖掘潜力，例如行程时间估计［11-12］、OD矩阵估计［13-15］和排队长度估计［16-18］等。然而在信号控制优化方面，以电警数据为数据源的研究还较少。Nie 等［19］基于电警数据计算出MinGT 模型与MaxGT 模型所需的交通参数，但是受限于感应控制的框架，其对于电警数据的利用并不充分。因此，在目前城市道路广泛布设电警检测器的背景下，本文充分挖掘电警数据蕴含的交通流信息，构建了基于电警数据的单点自适应信号控制优化框架，提出仅以电警数据为数据源的车辆到达预测方法，随后建立以最小化总延误为目标的自适应信号控制优化模型，对于当前城市道路中的单点信号控制优化具有理论意义与应用价值。

1 研究场景与控制框架

研究场景为四肢交叉口（目标交叉口）及其四个上游交叉口，所有交叉口的各进口道均布设有电警检测器。考虑到我国城市道路交叉口绝大部分情况下右转流向不受灯控，因此仅考虑左转与直行车道的电警检测器。利用上游交叉口的电警检测器能够实时获取左转与直行方向前往目标交叉口的车流，如图1所示。

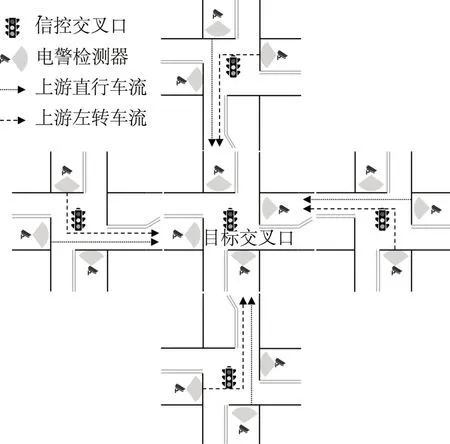
图1 研究场景Fig.1 Study scenario

控制框架如图2 所示。在车辆到达预测部分中，首先根据历史电警数据，得到不同上游流向在下游的转向比以及区分下游流向的上游右转流率，同时利用高斯混合模型对路段行程时间参数进行估计，随后以上游实时电警数据为输入，通过基于截断正态分布的车队离散模型得到到达率预测值。在信号控制优化部分中，首先确定滚动优化时长，随后基于到达率预测值，使用IQA 模型进行计算目标函数（交叉口总延误），利用动态规划求解各相位绿灯时间。

图2 控制框架Fig.2 Control framework

2 车辆到达预测

自Robertson模型［20］提出以来，车队离散模型在车辆到达预测中得到了广泛使用。Robertson模型假设车辆行程时间服从移位几何分布，未考虑行程时间的上限，后续研究表明其在许多场景下并不适用［21-22］。姚志洪等［23］考虑了车辆行程时间的有界性，采用截断正态分布拟合路段行程时间，利用网联车数据动态标定模型参数，然而该方法受限于网联车较低的渗透率。在上述研究中，路段行程时间并不包含车辆在下游交叉口的停车延误。因此在电警环境下，需要选取合适的聚类算法将未经历排队的车辆聚为一类，根据其行程时间估计路段行程时间参数。

2.1 路段行程时间参数估计

考虑到上游左转与直行车流在起步阶段的速度差异，对路段中这两类检测车辆进行区分。记上游流向u的车辆i离开上游的时刻为，到达下游的时刻为，其中u∈{left，str}，则其行程时间为tu，i=在一个TOD时段内有车辆行程时间集合{tu，i}，对其进行聚类可得到未经历排队车辆的行程时间集合，记为{τu，i}。

假设路段行程时间服从截断正态分布，则高斯混合模型（Gaussian Mixture Model，GMM）能够很好完成以上聚类任务。高斯混合模型是一种常见的聚类算法，其假设观测变量隶属于多个不同的正态分布。对车辆行程时间集合{tu，i}进行聚类，取均值最小的一类作为路段行程时间，得到其分布参数，包括均值μu、方差σu、最小值τu，min和最大值τu，max。定义高斯混合模型为

式中：tu为上游流向u的车辆行程时间，ϕ(x)为标准正态分布的概率密度函数，μz为均值，σz为标准差，K为混合成分数量，下标z=1，2，…，K表示第z个混合成分，αz为权重系数，满足

步骤1：遍历混合成分数量K=2，3，…，Kmax，采用期望最大化（Expectation-Maximization，EM）算法［24］迭代估计以上高斯混合模型的参数θK={α1，μ1，σ1，…，αK，μK，σK}。为了保证最佳聚类效果，计算不同混合成分数量对应的贝叶斯信息准则（Bayesian Information Criterion，BIC）。

步骤2：选择使得BIC 最小的混合成分数量K，得到模型参数θK。取均值最小的混合成分z0=计算路段行程时间参数，其中均值为μu=，方差为σu=σz0，最小值为τu，min=min{tu，i}，最大值τu，max通过求解以下方程获得

2.2 基于截断正态分布的车队离散模型

根据2.1部分所估计参数，上游流向u路段行程时间的概率密度函数为

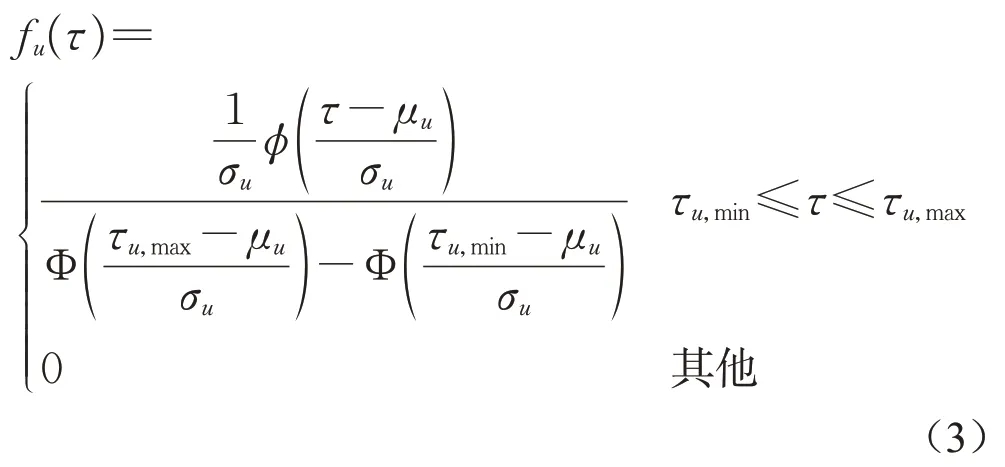
式中：Φ(x)为标准正态分布的累积分布函数。

为了与后续信号控制优化相适应，对路段行程时间进行秒级离散化处理，其概率质量函数为

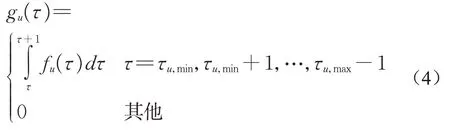
对车辆离开上游的时刻同样进行秒级离散化处理。记t为整数时刻，时间间隔t表示时间段[t-1，t)。在时间间隔t内若上游流向u有n辆车通过，则记流率qu(t)=nveh·s-1。上游流向u在下游流向m的转向比记为ηu，m，根据TOD时段历史数据标定。由于右转流向未布设电警检测器，因此上游右转流率qright，m采用TOD时段平均值且按下游流向m进行区分。根据上游实时电警数据qu(t)以及概率质量函数gu(τ)，下游流向m时间间隔t的到达率为

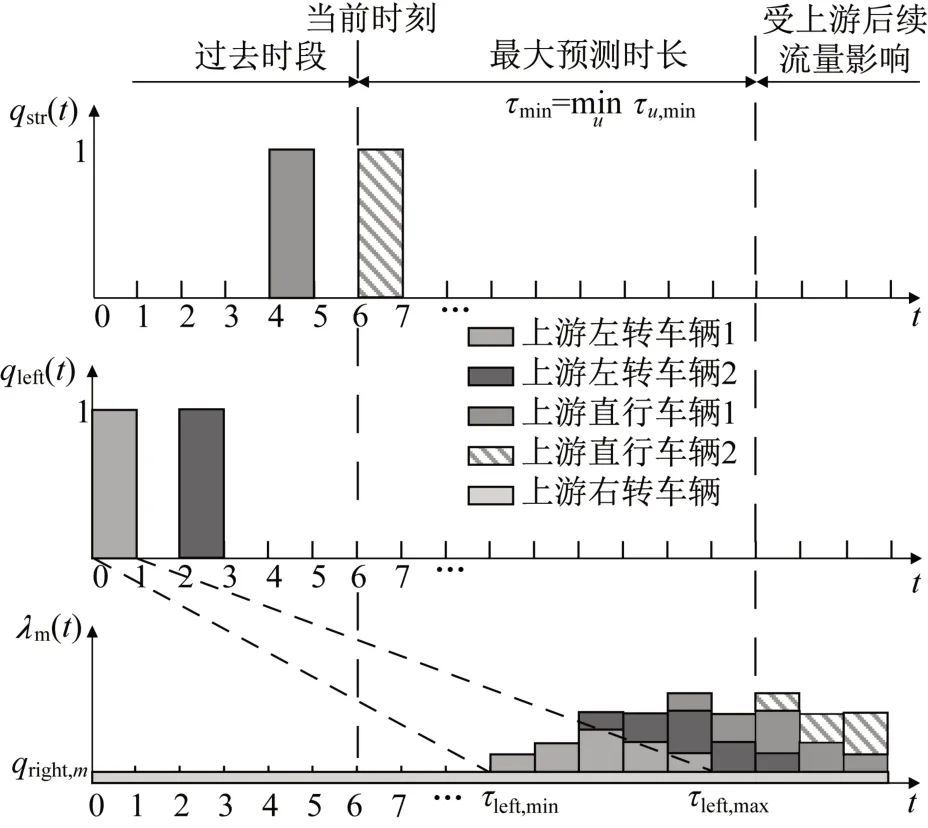
图3 车队离散模型示意Fig.3 Illustration of platoon dispersion model

3 信号控制优化

2.2部分实现了根据上游实时电警数据对下游到达率的预测，路段l到达率的最大预测时长为τl，min，因此整个交叉口的最大预测时长为各路段最大预测时长的最小值其中L为路段集合。采用滚动优化的方式，以交叉口总延误最小为目标函数，基于到达率预测值对信号控制参数进行实时优化。如图4 所示，滚动优化时长可大于最大预测时长，在最大预测时长结束时刻进行下一次信号更新。值得注意的是，如果下一信号更新时刻处于放行相位的黄灯或清空时间，则将其前移至绿灯结束时刻。

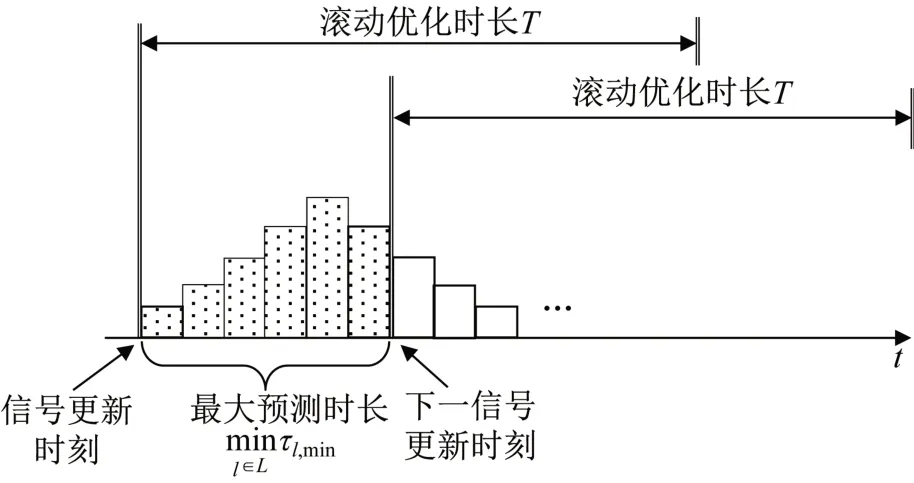
图4 滚动优化Fig.4 Rolling horizon

如图5 所示，对于每个滚动优化时长T，按照一定的相位结构分配各相位的绿灯时间gj，sj为第j个相位的绿灯结束时刻。其中，第一个相位是信号更新时刻放行相位的延续，记该相位为p0，已放行时间为g0。除第一个相位外，后续相位在绿灯开始前有黄灯时间y以及清空时间r。

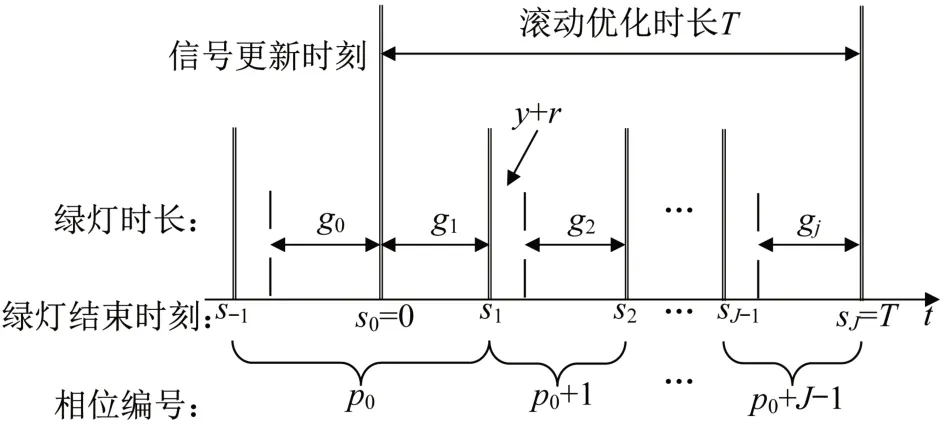
图5 绿灯时间分配示意Fig.5 Illustration of green time split

相位结构如图6所示，其中搭接相位2、3不能同时出现，相位6、7同理，保证同一流向在一个周期中仅放行一次。考虑到相位的周期性，定义相位p+8k（1 ≤p≤8，k为正整数）与相位p含义相同。记当第一个相位为p0时搭接相位的序号集合为，即∀j∈，有p0+j-1 ∈{2，3，6，7}。记第j个相位的最小与最大绿灯时间分别为gj，min和gj，max，其中搭接相位可以跳过，最小绿灯时间设为0，其他相位最小绿灯时间均大于0。模型中的其他参数与变量如表1所示。

图6 相位结构Fig.6 Phase structure

表1 模型参数与变量Tab.1 Model parameters and variables

3.1 目标函数

使用交叉口总延误最小作为目标函数，根据增量排队累积（Incremental Queue Accumulation，IQA）方法［25］，滚动优化时间内第j个相位的总延误为所有流向所有时刻的排队车辆数之和

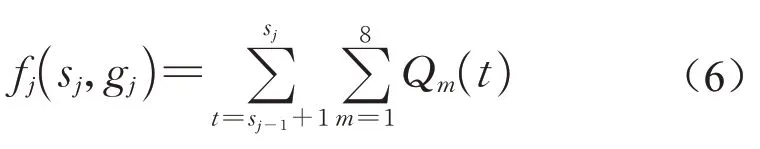
目标函数为最小化各相位总延误的加和

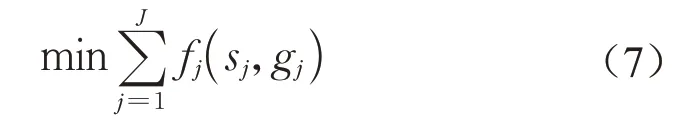
根据流量守恒，时刻t的排队车辆数由t-1 时刻的排队车辆数以及时间间隔t的到达和离去车辆数决定，相位初始排队车辆数等于上一相位结束时的排队车辆数

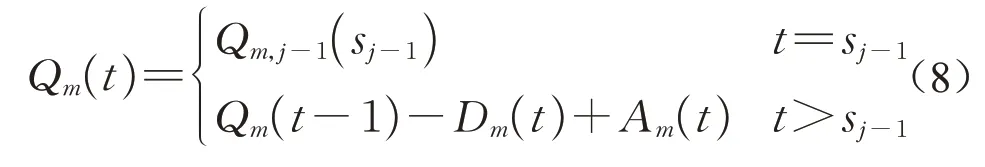
式中：Am(t)为时间间隔t的到达车辆数，Am(t)=λm(t)Δt，其中Δt=1s，λm(t)为时间间隔t的预测到达率。Dm(t) 为时间间隔t的离去车辆数，Qm，j-1(sj-1)为第j-1个相位结束时的排队车辆数。

记p=p0+j-1 为当前相位编号，p'=pj-1(sj-1)为上一放行相位编号，Mp为相位p的放行流向集合。考虑到相位搭接情况的多样性，Dm(t)的计算可分为以下4种情况：

（1）若流向m在两相位中都被放行，即m∈Mp∩，则时间间隔t的离去车辆数为饱和流率与当前排队车辆数之间的较小值

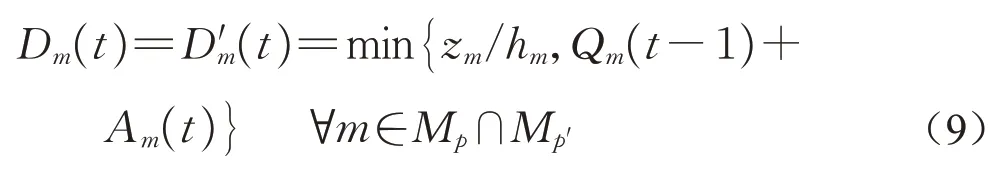
（2）若流向m在两相位中都不被放行，即m∉Mp∪，则离去车辆数始终为0

（3）若流向m从当前相位才开始放行，即m∈，则在前y+r秒分别为上一放行相位的黄灯时间与全红时间，后续l1秒为绿初损失时间，因此前y+r+l1秒离去车辆数为0

（4）若流向m仅在上一相位放行，即m∈，由于前y秒为上一相位的黄灯时间，因此该流向在前y-l2秒内继续放行，l2为黄末损失时间

3.2 约束条件

3.2.1滚动优化时长约束

滚动优化时长等于各相位时长的加和，除第一个相位时长等于绿灯时间外，后续未跳过相位的时长还包括前置的黄灯时间与清空时间

式中：J为滚动优化时间内的相位数，h(gj)表示绿灯时间为gj的相位时长

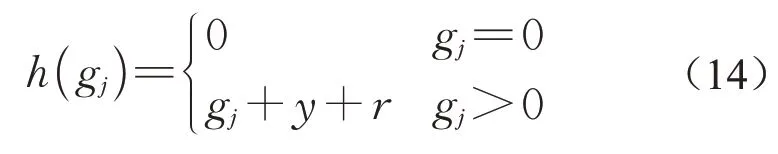
3.2.2绿灯时间约束

由于第一个相位是信号更新时刻放行相位的延续，因此绿灯时间约束为

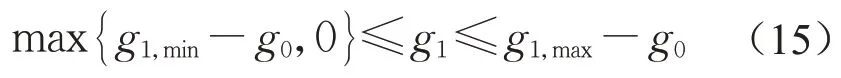
后续相位的绿灯时间则仅受最小与最大绿灯时间限制

3.2.3搭接相位约束

对于第2个相位，由于第1个相位在信号更新时刻前已放行，如果第1、2个相位均为搭接相位，则绿灯时间为0

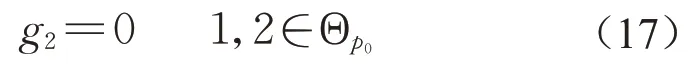
对于后续相位，两个搭接相位不能同时出现

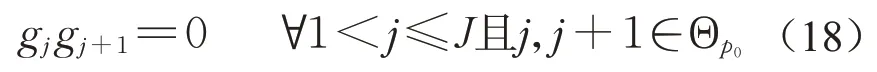
3.2.4整数约束

由于到达率预测值为秒级离散，因此各相位的绿灯时间均为整数：

3.3 基于动态规划的求解算法

以上整数规划问题利用枚举法求解困难。考虑到滚动优化时间内的信号控制切换实际上是一个多阶段决策过程，每个相位可看作一个阶段，绿灯结束时刻sj为状态变量，绿灯时长gj为决策变量，因此可采用动态规划算法进行求解。

第j个相位的绿灯结束时刻下限sj，min可根据各相位的最小绿灯时间累加计算

考虑到搭接相位的最大绿灯时间可能各不相同，因此在累加计算绿灯结束时刻上限sj，max时需要比较两搭接相位的最大绿灯时间

不考虑搭接相位约束，绿灯时间gj的取值范围Gj(sj)如下所示。对于第1个相位，绿灯时间与其结束时刻相等。对于后续相位，绿灯时间受限于最小与最大绿灯时间，并且需要使得sj-1=sj-h(gj)在其上下限内。特别地，如果sj=T则说明该相位可在之后延续，故无最小绿灯时间限制。

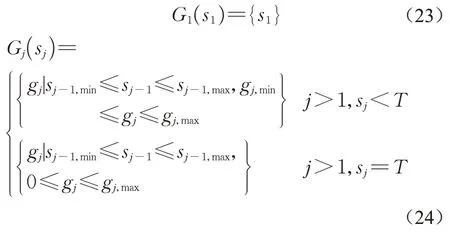
进一步考虑搭接相位约束，导致两搭接相位同时出现的绿灯时间gj取值范围为

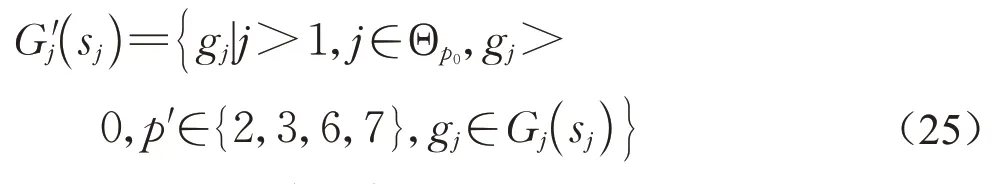
式中：p'=pj-1(sj-1)为上一放行相位编号。

动态规划算法详述如下：

（1）向前搜索

步骤1：初始化j=1，初始目标函数F0(s0)=0，初始排队长度Qm，0(s0)=Qm，0，初始放行相位编号p0(s0)=p0。

步骤2：遍历sj=min{sj，min，T}，min{sj，min，T}+1，…，min{sj，max，T}，求解如下最优化问题

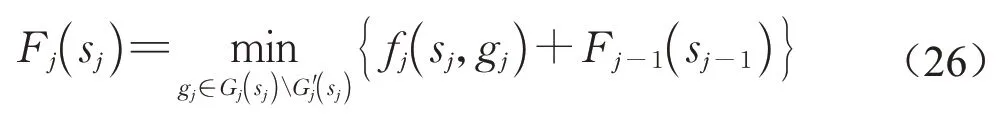
特别地，当j＞2 时，若第j个相位为搭接相位3或相位7，需要额外判断若前一搭接相位跳过，目标函数是否更优

步骤3：若sj，min＜T，更新j=j+1，回到步骤2；否则结束向前搜索，前往步骤4。

（2）向后搜索

4 仿真验证

4.1 仿真模型构建

本文在微观仿真软件SUMO中对浙江省桐乡市真实路网进行建模，采用Python 实现上述车辆到达预测以及信号控制优化模型，通过TraCI 接口与SUMO进行交互。图7展示了庆丰北路-逾桥中路交叉口及其四个上游交叉口的位置关系，东、南、西、北四个方向交叉口与目标交叉口的距离分别为1150m、350m、910m及450m。目标交叉口如图8a所示，除右转车道外所有车道均布设有电警检测器。使用2020年12月3日上午8：00—9：00由电警检测器采集到的流量和转向比对仿真模型进行标定，各受控流向的流量如图8b所示。仿真车辆全部由小汽车构成，采用Krauss跟驰模型，各路段限速均为50km·h-1。

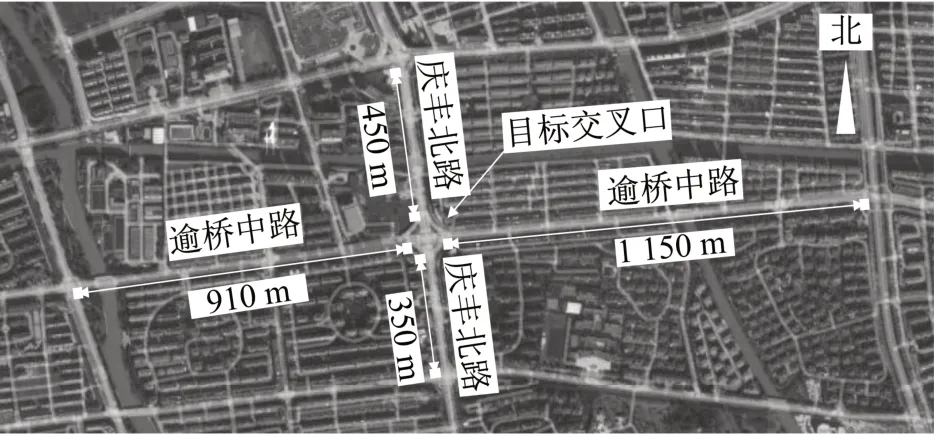
图7 仿真验证场景Fig.7 Validation scenario

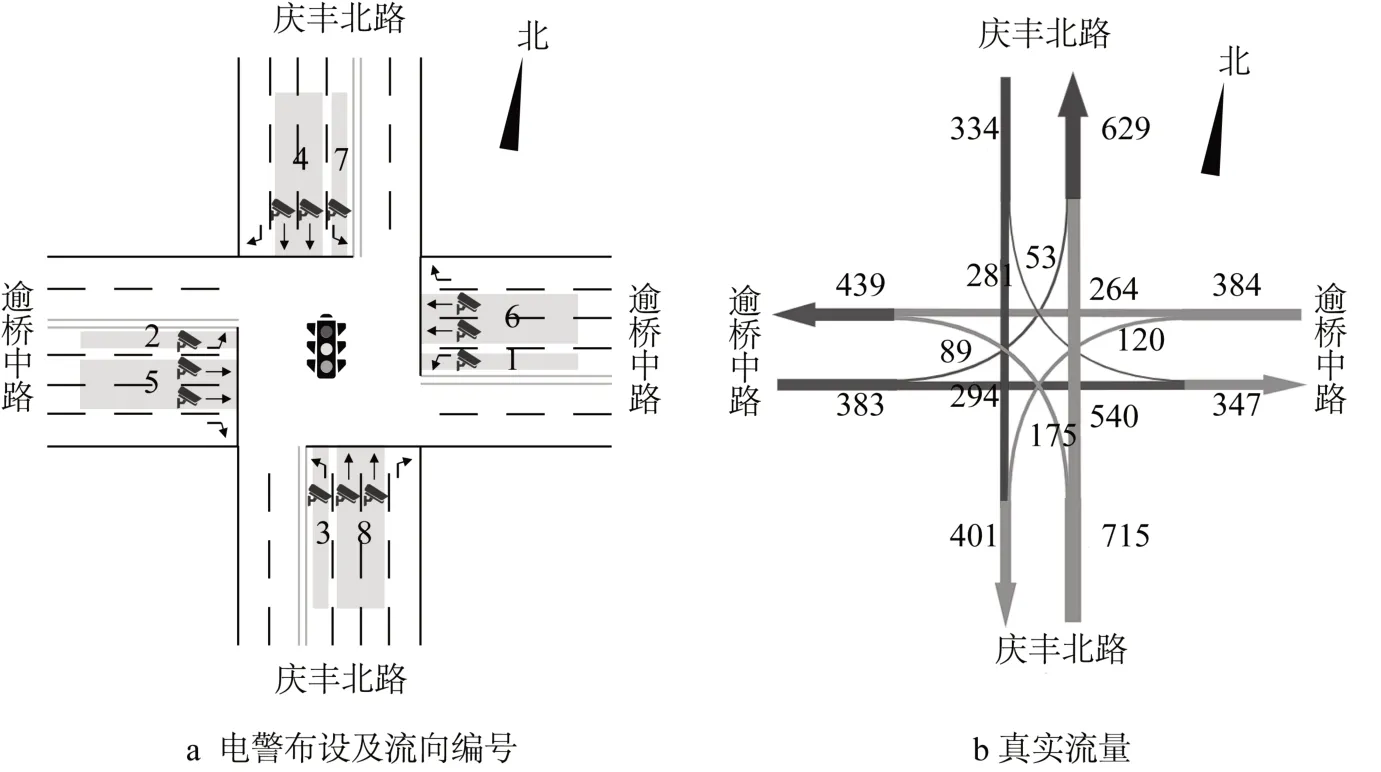
图8 目标交叉口Fig.8 Target intersection

为了验证不同需求场景下的优化效果，在真实数据标定流量的基础上定义4 种需求场景。如表2所示，场景II 为真实流量，场景I、场景III 与场景IV的流量分别为场景II 的0.75、1.25 与1.5 倍。各场景的仿真时间为130min，其中前10min为预热时间。使用基于灯组的定时控制方法［26］计算各场景下的固定信号配时方案，优化目标为最小Webster 延误，每个流向为一个灯组，各灯组的最小绿灯时间均为10s，黄灯时间为3s，清空时间2s，损失时间为4s，结果周期时长与目标函数值如表2所示。

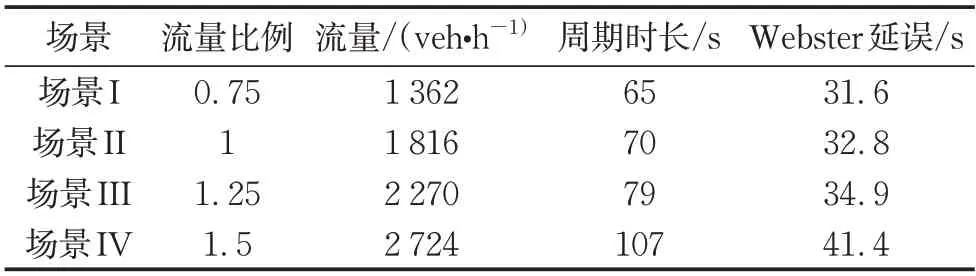
表2 需求场景Tab.2 Demand scenarios

后续验证分为两个步骤进行：①在最优灯组配时下，使用5组不同的随机种子对各场景进行仿真，通过匹配后的上下游电警数据估计各场景的路段行程时间参数；②根据上一步估计的参数标定各场景下的车队离散模型，使用5组不同的随机种子对本文方法的控制效益（车均延误、平均排队长度）进行验证。

4.2 路段行程时间参数估计

以场景II东进口上游直行车辆为例，图9a展示了不同混合成分数量对应的BIC 值，根据折线图的最低点取混合成分数量为2，拟合结果如图9b所示。取均值最小的混合成分作为非排队车辆混合成分，均值与标准差分别为90.60s与7.47s，最小值与最大值分别为69.77s与104.40s，将其作为场景II该路段上游直行流向的路段行程时间参数。

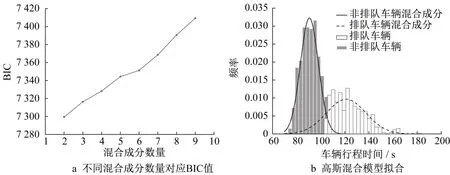
图9 路段行程时间参数估计示意Fig.9 Illustration of link travel time parameters estimation

路段行程时间均值与标准差的估计误差如图10 所示。真实值通过获取SUMO 中到达停车线前未停止的车辆得到。所有场景中均值与标准差的估计误差均小于3s，其中场景I均小于2s，场景IV均小于1.5s。各场景均值的平均估计误差分别为0.76s、0.88s、0.93s 与0.91s，标准差的平均估计误差分别为0.8s、1.01s、1.04s与0.8s，说明随着流量的增加，非排队车辆比例的下降可能导致估计误差的增加，但更多的流量也提供了更多的样本，因此在场景IV中估计误差有所降低。

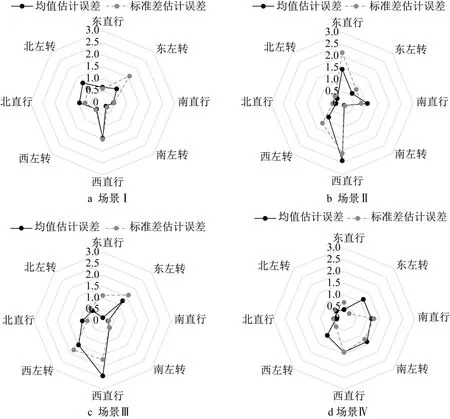
图10 路段行程时间参数估计误差Fig.10 Estimation error of link travel time parameters

4.3 信号控制优化效果

使用5组不同的随机种子，在4种场景下对本文方法的进行验证，控制效益选取车均延误与平均排队长度，其中平均排队长度为各受控流向每时刻排队长度的平均值，排队长度定义为最后一辆速度低于5km·h-1的车辆离停车线的距离。搭接相位的最小与最大绿灯时间分别设为0s与20s，其他相位分别设为5s 与40s。黄灯时间设为3s，绿初与黄末损失时间均设为2s。各场景的最大预测时长分别为22s、21s、20s 和22s，滚动优化时长取40s，后续将对滚动优化时长的取值进行验证。为了验证本文方法的有效性，使用感应控制与最优灯组配时作为对比。其中感应控制由布设在目标交叉口各受控流向的电警设备实现，最小与最大绿灯时间分别为5s 与40s，黄灯时间为3s，最大间隔为3s。

不同场景下的控制效益如图11 所示。在所有场景下本文方法的控制效益均较灯组配时大幅改善，车均延误分别减少41.7%、34.2%、35.4%和37.9%，排队长度分别减少48.8%、40.5%、41.8%和43.1%。对比感应控制，车均延误分别减少4.0%、2.6%、5.2%和12.9%，排队长度分别减少6.1%、5.4%、9.7%和15.8%，在需求更高的场景IV下改善更为明显。转较高的排队长度也说明了这一点。

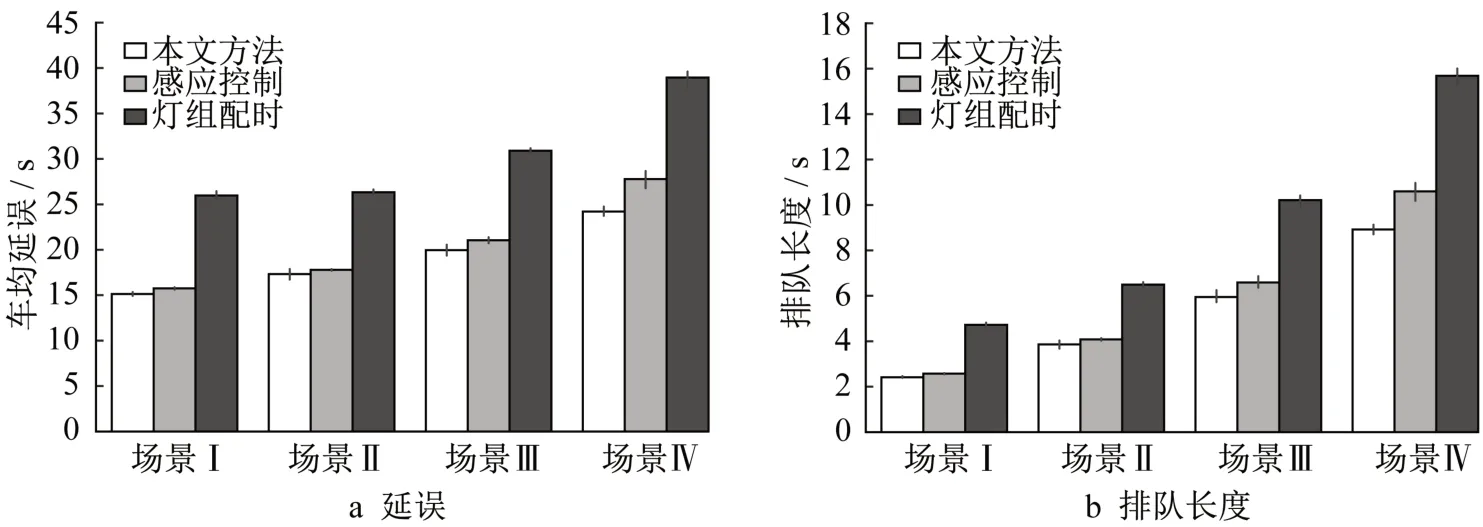
图11 不同场景控制效益比较Fig.11 Comparison of control benefits in different scenarios

图12 和图13 分别展示了场景I 与场景IV 不同流向的控制效益比较。在场景I 中南进口延误改善明显，西进口持平，其余进口延误略高于感应控制，但由于南进口流量显著高于其他进口，因此总体延误有所改善。对于排队长度指标，南进口同样改善明显，东进口略高于感应控制，其他进口基本持平。在场景IV 中，除东左转与北左转流向外，其余流向延误均有所改善。东左转显著突出的延误水平是由于上游电警无法判断单个车辆在下游的流向，进而导致部分周期左转相位放行不充分，图13b 中东左表3 展示了不同滚动优化时长下的控制效益，车均延误与排队长度为所有场景下的平均值。作为对比，感应控制的车均延误为21.69s，平均排队长度为6.00m。在不同滚动优化时长下各指标均优于感应控制，且在测试范围内随着滚动优化时长的增加，车均延误以及排队长度不断减低，这是由于更长的滚动优化时长能够考虑更多的相位组合情况。本文信号控制优化模型在R7 4800H处理器上运行，单次计算时间随滚动优化时长增加，但均小于0.5s。在实际应用中应考虑使用C++编码，并结合设备算力选择最优的滚动优化时长。

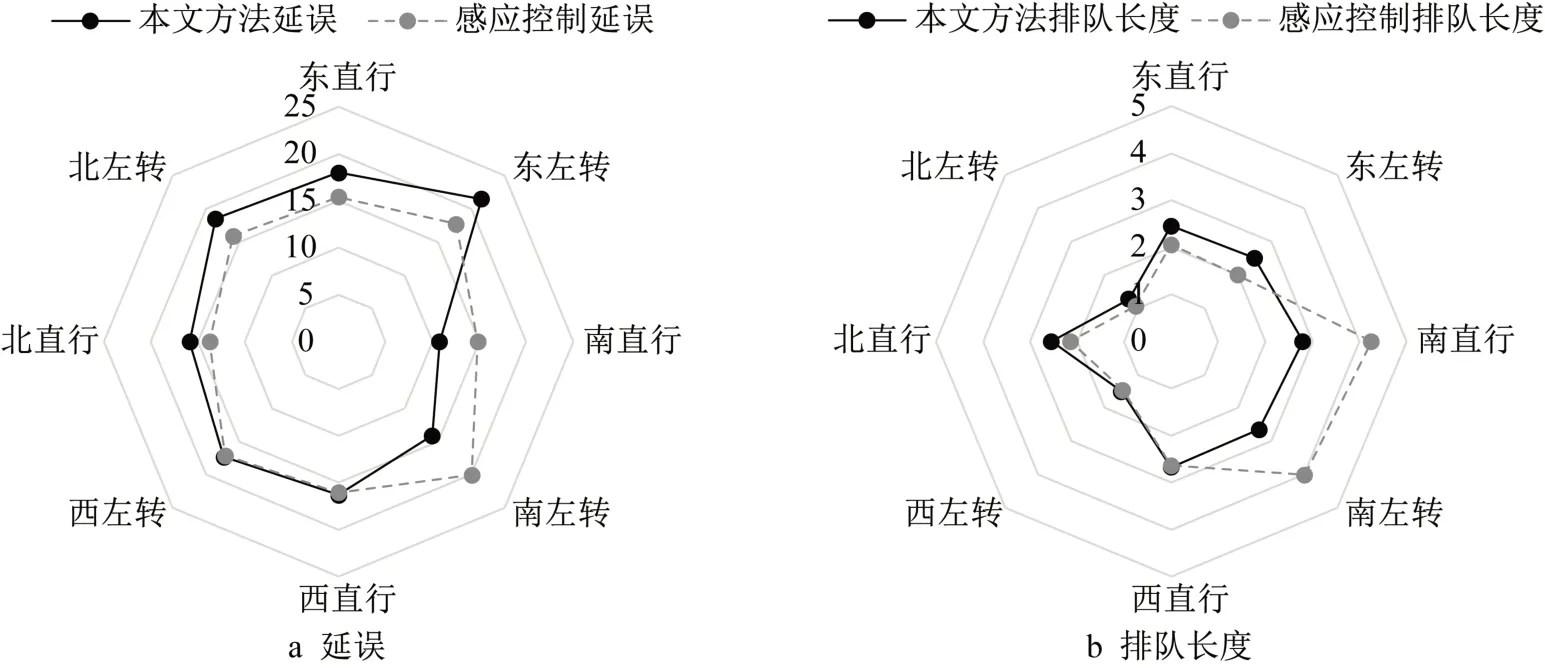
图12 场景I控制效益比较Fig.12 Comparison of control benefits in scenario I

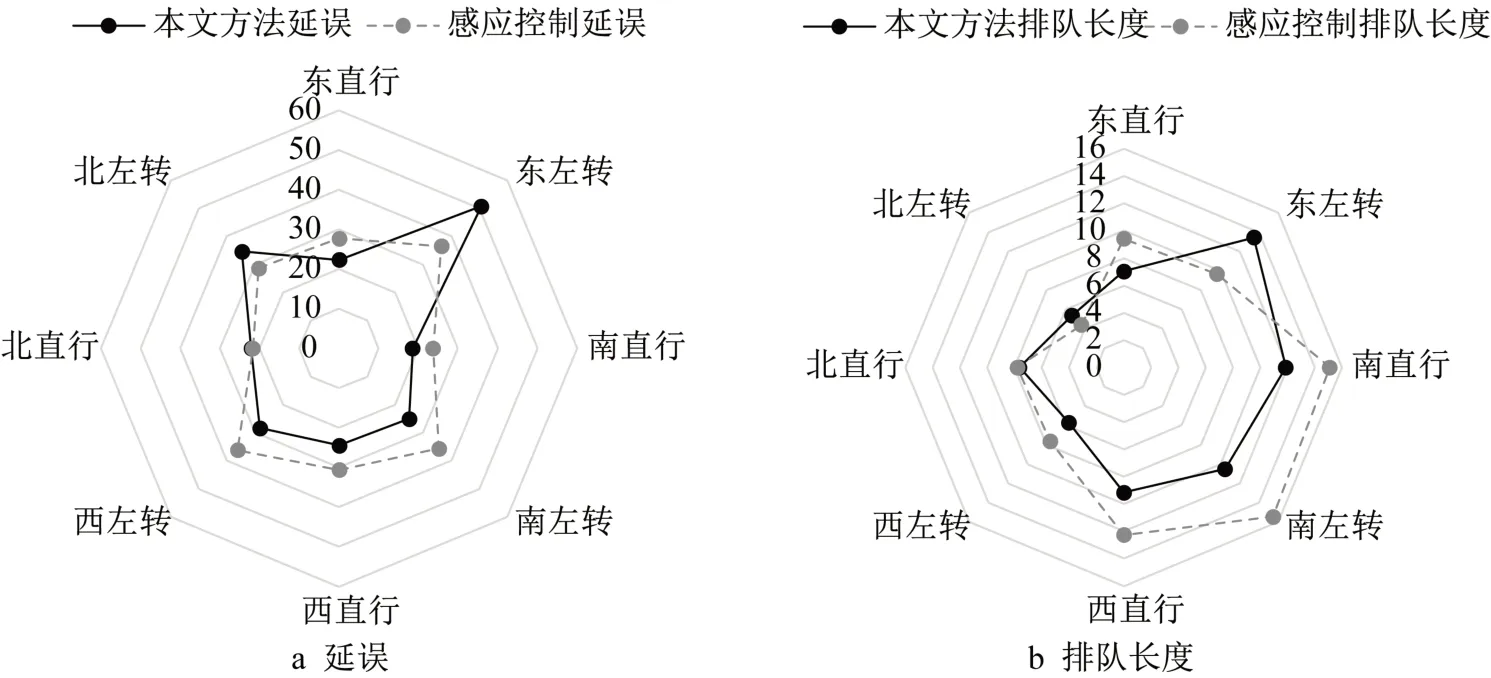
图13 场景IV控制效益比较Fig.13 Comparison of control benefits in scenario IV

表3 不同滚动优化时长下的控制效益Tab.3 Control benefits under different planning horizon

5 结语

本文充分挖掘电警数据的特性，构建了基于电警数据的单点自适应信号控制优化框架。本文的研究场景包括目标交叉口及其四个上游交叉口，所有交叉口的各进口道均布设有电警检测器。首先根据历史电警数据，利用高斯混合模型估计路段行程时间参数，进而标定基于截断正态分布的车队离散模型，随后基于到达率预测值建立了以最小化总延误为目标的自适应控制优化模型，考虑该模型为整数规划模型，采用动态规划算法进行求解。

在不同需求场景下对上述模型进行验证。验证结果表明，在路段行程时间参数估计方面，均值与标准差的估计误差均小于3s。与最优灯组配时相比，本文方法的车均延误与排队长度在所有场景下均大幅改善，分别减少34.2%和40.5%以上。与感应控制相比，本文方法在高需求场景下改善效果明显，分别减少12.9%和15.8%，在其他场景下也分别有2.6%和5.4%以上的改善。滚动优化时长的增加有助于控制效益的改善，但会导致计算时间的增加，需要根据设备算力选择最优的滚动优化时长。

然而，该方法也存在一些局限性。电警设备的漏检会导致到达率预测值的偏差，但在文中未予以考虑，后续可从上游车辆车头时距序列着手对漏检进行修复。另外，由于上游电警无法判断单个车辆在下游的流向，如果左转车辆过多则可能出现放行不充分的现象。因此，未来可融合网联车数据，或利用布设在停车线前的线圈得到流向排队长度下限，从而改善模型的优化效果。

作者贡献声明：

骆旅舟：构建自适应控制框架；实现车辆到达预测及信号控制优化算法；进行仿真验证；撰写论文文本

谈超鹏：参与构建自适应控制框架；修改论文文本

唐克双：提供方法思路与写作指导