变量相对重要性评估的方法选择及应用*

朱 训 顾 昕

(华东师范大学教育心理学系,上海 200062)

1 引言

在当前心理学研究关注高维度大数据的背景之下,研究涉及的变量越来越多,变量的重要性评估变得越发重要。例如,个人、家庭、学校、社会层面的诸多因素都可能影响学生校园欺凌行为。简单来说,变量重要性表示其在预测和解释因变量时的贡献。相对重要性评估能够帮助研究者探索、验证和细化理论。比如家庭因素和学校因素哪一个对于校园欺凌行为的影响更大,在家庭因素中亲子互动关系、父母管教方式、父母情绪处理等变量的重要性排序又是怎样的。相对重要性评估对变量的有效利用格外重要。首先,探索变量的相对重要性能够帮助决策者确定投入的重点。尽管师生关系、教师对待欺凌的态度、校园文化、班级大小等因素都会影响校园欺凌行为,但在资源和时间有限的情况下,管理人员可能不得不选择更具成本和时间效率的项目,例如是开发课程帮助学生认识校园欺凌还是加强教师处理欺凌事件技巧的培训更为迫切。此外,评估变量的相对重要性能够帮助决策者确定需要接受干预的个体。如果确定个体的自尊水平、身体表征是校园欺凌行为发生的重要因素,就可以预先识别出可能涉及欺凌事件的高危学生群体并进行早期介入,避免或减少欺凌行为的发生。因此,变量相对重要性的方法与应用研究具有重要的现实意义。

变量相对重要性的研究是从回归模型开始的,Darlington (1968)在Psychological Bulletin期刊的文章最早讨论了相对重要性的评估指标,包括相关系数、偏相关系数、标准化回归系数等,但都被证明存在明显缺陷。后来,心理学研究者提出了优势分析(Budescu,1993;Azen & Budescu,2003)、相对权重(Johnson,2000)等相对重要性评估指标,并给出了相对重要性的一般定义：同时考虑单独效应与偏效应时,每一个自变量对R2(回归模型测定系数,coefficient of determination)的贡献比例(Johnson & LeBreton,2004)。这些指标的含义和计算方法不同,适用情境也不尽相同。

许多应用相对重要性方法的实证研究只汇报了各变量重要性指标的估计值和由此得到的排序,而忽略假设检验的结果。但是,假设检验是统计推断的必要工作。在计算变量的相对重要性指标后,研究者最好利用假设检验推断变量相对重要性及其差异的显著性。例如,一个自变量的重要性是否显著地大于另一个自变量,或是否有足够的数据证据支持变量的重要性排序。研究者通常使用bootstrap 抽样方法计算指标估计值的标准误并构造置信区间(Azen & Budescu,2003;Tonidandel et al.,2009)。同时,也有基于贝叶斯因子的相对重要性评估方法,其优势是能够检验三个及以上自变量的相对重要性次序,并给出数据支持重要性次序的证据(Gu,2021)。

近年来,相对重要性研究被拓展到其他一些模型中,如多因变量回归模型(Azen & Budescu,2006;LeBreton & Tonidandel,2008)、Logistic 回归模型(Azen & Traxel,2009;Tonidandel & LeBreton,2009)、多水平模型(Luo & Azen,2013;Rights & Sterba,2019)、结构方程模型(Gu,2022)等。同时,研究者开发了许多统计软件用于计算变量相对重要性指标并推断其显著性,如R 包dominanceanalysis可以用于执行优势分析,R 包yhat 可以执行优势分析和相对权重分析,R 包bain 用于相对重要性的贝叶斯因子评估。优势分析和相对权重方法因其解释的直观性以及较完备的模型与软件支持,在心理学领域得到了广泛应用(Casillas et al.,2012;Richardson et al.,2021;Modersitzki et al.,2021)。

相对重要性的评估指标种类繁多,统计推断方法和模型的适用情形不同,但目前国内缺乏相关的文献综述和评论。本文通过相对重要性评估方法的论述与比较,帮助心理学研究者选取恰当的变量重要性评估指标和推断方法,并为相对重要性方法研究提供方向性建议。

2 变量相对重要性的评估指标

本节在回归模型下介绍几种常用的相对重要性指标,回归模型可表示为：

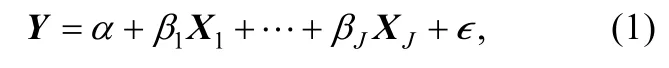
其中Y是长度为N(被试人数)的因变量,α是截距,X1,…,XJ是长度为N的J个自变量,β1,…,βJ是对应的回归系数,∈～N(0,σ2)是以σ2为方差的长度为N的残差向量。

为了便于解释说明,首先举一个简单的例子。如图1 所示,建立以考试成绩为因变量,学科能力、复习时长和焦虑程度为自变量的回归模型：

图1 回归模型例

并假设变量的相关系数矩阵如表1 所示。考试成绩和学科能力有强相关,复习时长会影响考试成绩,学生的焦虑程度与学科能力和复习时长有关。我们将分析学科能力、复习时长、焦虑程度在以上回归模型中的相对重要性。

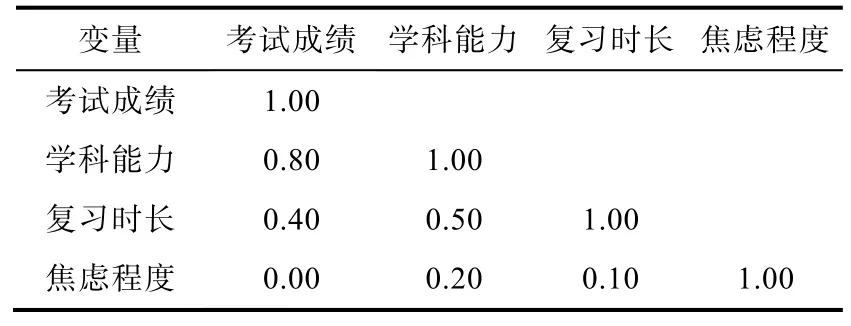
表1 变量的相关系数矩阵

2.1 相关系数与回归系数

因变量Y和各自变量Xj的相关系数rj是变量重要性的基础指标,代表自变量和因变量的相关性,衡量了自变量对因变量的独立影响与直接预测能力。但是,相关系数指标忽略了模型中的其他自变量,没有考虑自变量的相互影响。例如焦虑程度和考试成绩的相关系数r3=0,但焦虑程度和学科能力及复习时长有关,也会影响考试成绩。

标准化回归系数是心理学研究比较自变量重要性最常见的传统指标,它表示保持其他自变量不变,Xj对因变量Y的标准化偏效应,解释为Xj增加1 个标准差时,Y的预期变化。但是,标准化回归系数存在缺点,标准化回归系数的估计依赖模型中的其他自变量,一个自变量回归系数为零并不代表它一点也不重要,它的重要性可能被其他自变量隐藏。例如,根据表1 的相关系数矩阵,学科能力、复习时长和焦虑程度对应的标准化回归系数分别为-0 .17,但这并不意味着复习时长对考试成绩不重要。

由于相关系数和标准化回归系数都可以为负,一般使用它们的平方作为变量重要性指标。当自变量不相关时,相关系数等于标准化回归系数。但当自变量相关时,两者不一定相等。相关系数代表每个自变量的单独贡献,而标准化回归系数代表每个自变量在控制了其他自变量后的贡献,也即自变量对因变量的独特贡献。

心理学研究常涉及变量组,如社会经济地位(包括收入、职业、受教育水平等)和人格特质(包括开放性、宜人性、责任心等)。研究人员可能希望评估变量组在解释和预测因变量时的联合贡献,即变量组的重要性。相关系数、标准化回归系数及其乘积指标的另一个缺点是不能衡量变量组的重要性。一组变量的相关系数或标准化回归系数的和或平均值不能解释为变量组的联合效应,比如,学科能力和焦虑程度的标准化回归系数分别为0.83 和–0.17,但其联合效应并非为0.66。一组变量的乘积指标之和可能为负或小于单个变量的乘积指标,因此难于解释。此外,回归模型中的分类自变量,如职业与受教育水平,都需要转化为一组虚拟变量,分类变量的重要性无法用标准化回归系数衡量与比较。

2.2 R 2增量

回归模型R2增量 ΔR2是直观的变量重要性评估指标,它反映了自变量进入模型后因变量方差解释的增量,也即该自变量的独特贡献。变量Xj最后进入模型时的R2增量可表示为：

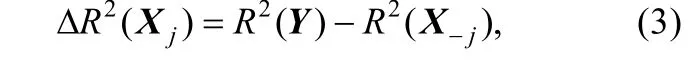
其中R2(Y)是模型总R2,R2(X-j)表示不包含自变量Xj的模型R2。R2增量方法能够衡量变量组的重要性,比如自变量X1,X2,X3的联合贡献可由它们同时进入模型时的R2增量 ΔR2(X1X2X3)=R2(Y) -R2(X-123)评估,其中R2（X-123）表示不包含自变量X1,X2,X3的模型R2。但与标准化回归系数类似,R2增量为零不代表自变量毫无作用,该变量对方差解释的贡献可能被其他先进入模型的变量隐藏。此外,所有自变量最后进入模型的R2增量之和不等于R2（Y）,不能表示R2的分解。如对于考试成绩的回归模型,由表1 相关系数矩阵可计算得到,R2（Y）=0.66,学科能力的R2增量 ΔR2(X1)=0.51,复习时 长 ΔR2(X2)=0.00,焦虑程度 ΔR2(X3)=0.03。

ΔR2(Xj)只考虑了Xj最后一个加入模型时的R2变化,而自变量可以有不同的进入次序,不同进入次序下R2增量的平均值被认为是更合适的重要性指标(Kruskal,1987)。例如,对于4 个自变量X1,X2,X3,X4,有4!=24种不同的进入次序,图2 呈现了部分自变量进入次序。对于进入次序（a）,X3的R2增量为R2(X1X2X3) -R2(X1X2),对于进入次序c,X3的R2增量为R2(X2X3) -R2(X2),其中R2(·) 表示包含相应自变量的模型R2。对所有进入次序下X3的R2增量求平均值即得到值得注意的是,所有自变量R2增量的平均值之和等于模型总体R2(Y),因此,?R2增量的平均值评估了各自变量对因变量方差解释的贡献比例。如对于考试成绩回归模型,(学 科能力)=0.57,(复 习时长)=0.08,(焦 虑程度) =0.01。该方法结合自变量的不同进入次序,较为全面地衡量自变量的重要性,并且能够分解模型R2。然而当自变量个数较多时,它需要付出较大的计算成本。对于J个自变量,该方法需要考虑J!个不同变量进入次序下的自变量R2增量,当J=10时,共有上百万种情形。

图2 自变量加入模型的不同次序

2.3 Shapley 值

事实上,自变量产生的R2增量仅与它加入的自变量集有关,而与这个自变量加入前后的其他变量次序无关。例如图2 中次序(a) 和(b) 下X3的R2增量相同,都为R2(X1X2X3) -R2(X1X2)。因此,只需考虑自变量可以进入的变量子集,这种变量子集可以是空集或是包含一个或多个自变量的集合。如图3 表示了X3可进入的子集。随后计算进入不同子集后R2增量的加权平均值指标,这里使用加权平均值是因为变量进入各子集的概率可能不同。

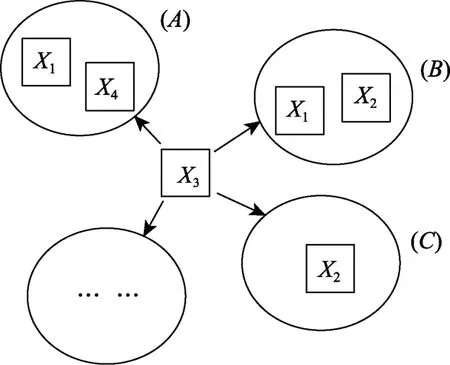
图3 自变量可进入的子集

Shapley 值分解就是基于这样的思想。Shapley值是数学家Lloyd Shapley 在合作博弈论的背景下提出的(Nandlall & Millard,2019),用于衡量玩家的参与对合作游戏结果得分的影响。玩家j对参与情况(即参与时游戏中已有玩家)的独特贡献就是玩家j加入后得分的变化,Shapley 值是玩家加入所有参与情况的独特贡献的加权和,而所有玩家的Shapley 值之和就是全部玩家参与时的游戏得分。将线性回归模型和Shapley 值方法结合,自变量即是参与游戏的玩家,游戏的得分为R2,玩家的独特贡献是自变量加入变量子集带来的R2增量。变量Xj的Shapley 值用S(Xj)表示。例如,对于4 个自变量X1,X2,X3,X4,图3 呈现了自变量X3可能加入的子集。X3进入子集(A)的R2增量为R2(X1X3X4) -R2(X1X4),子集(A)大小为2,自变量总数为4,因此X3进入子集(A)的概率为进入子集(C)的R2增量为R2(X2X3) -R2(X2),子集(C)大小 为 1,因此X3进入子集(C)的概率为进入所有可能子集R2增量的加权平均值即为S(X3)。对于考试成绩回归模型,S(学科能力)=0.57,S(复习时长)=0.08,S(焦虑程度)=0.01。Shapley 值同样能够分解R2,另外子集思想的引入有助于提升计算效率。对于J个自变量,该方法需要考虑的子集数量为2J-1 个,当J=10 时,共有一千多种情形。

2.4 优势分析

另一种考虑变量进入子集的方法是优势分析(dominance analysis,Azen & Budescu,2003),其使用变量成对比较,定义了三种优势模式：完全优势、条件优势和一般优势。完全优势比较两个自变量对它们可加入的公共变量子集的R2增量。例如对4个自变量X1,X2,X3,X4,X1和X2可加入的公共变量集是空集{.}、{X3}、{X4}和{X3X4}。若在这些子集中加入X1比加入X2都能得到更多的R2增量,则1X完全优于X2。

完全优势模式是严格的,当模型中有多个自变量时,常常不能识别出完全优势,例如X1和X2分别加入空集的R2增量R2(X1) ＞R2(X2),而分 别 加 入{X3}的R2增量 (R2(X1X3) -R2(X3))＜(R2(X2X3) -R2(X3))。为此Azen 和Budescu (2003)引入了另外两种较为宽松的指标：条件优势和一般优势。条件优势比较两个自变量加入相同大小的变量子集的R2增量平均值,对每一种子集大小,若1X的R2增量平均值都大于X2,则说明1X有条件优于X2。当然条件优势也可能无法识别。一般优势比较两个自变量条件优势指标的平均值,考虑不同变量子集大小,若X1的R2增量的总体平均值大于X2,则说明X1一般优于X2。完全优势必然导致条件优势,条件优势又必然导致一般优势。变量Xj的一般优势指标用d(Xj)表示。

以考试成绩回归模型为例,表2 展示了优势分析结果,k为变量加入的子集大小。自变量加入空集的R2增量即为自变量与因变量相关系数的平方,例如X1加入空集的R2增量为0.64(见表2 中k=0平均行)。X1加入{X2}的R2增量R2(X1X2) -R2(X2)=0.48,X1加入{X3}的R2增量R2(X1X3) -R2(X3)=0.67,因 此X1加 入 大 小 为k=1的子集的R2增量平均值为0.57 (见k=1 平均行)。1X的一般优势指标为各条件优势指标的平均值(见总平均行)。由表2 可知,对于解释和预测考试成绩,学科能力完全优于复习时长和焦虑程度。复习时长和焦虑程度之间不存在完全优势和条件优势,通过比较一般优势指标可得复习时长一般优于焦虑程度。

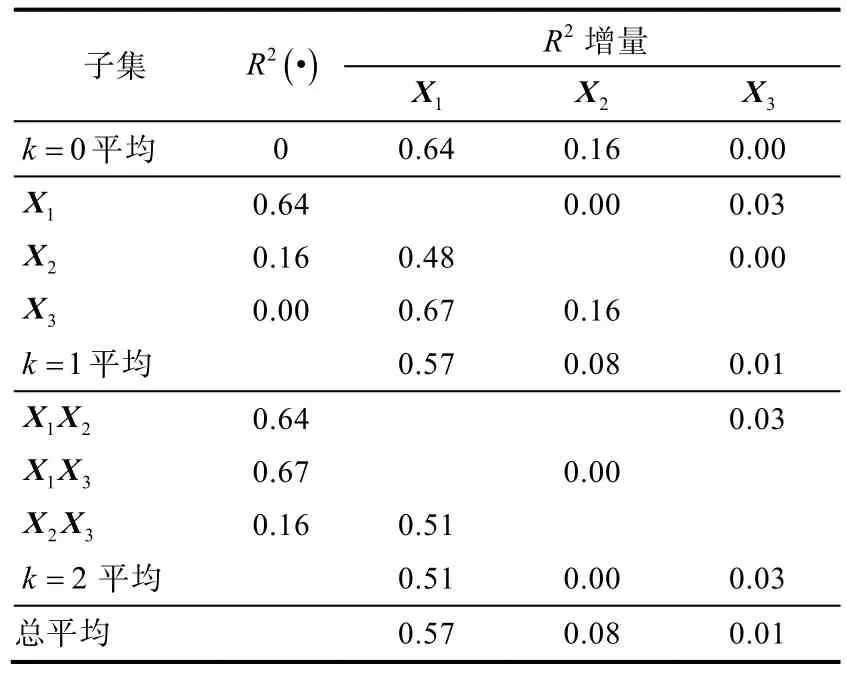
表2 优势分析结果

一般优势指标同样具备分解R2的性质,所有自变量的一般优势指标之和等于模型R2(Y) 。一般优势指标评估了自变量对因变量方差解释的贡献,完全优势和条件优势则提供了更多重要性模式的信息。此外,优势分析可以获得有限制的变量相对重要性,在模型中固定包含一些自变量,检验其他自变量的相对重要性。

尽管不同次序R2增量的平均值、Shapley 值、一般优势分析指标的含义不同,但以上三种方法得到完全相等的变量重要性度量：

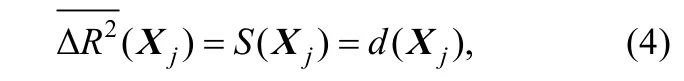
并且具有相同的性质：(1)衡量自变量对因变量方差解释的平均贡献;(2)分解R2,即将对因变量的方差贡献分配给每一个自变量;(3)能够衡量变量组的重要性,一组变量的联合重要性为组内各变量的重要性之和,例如对于一般优势分析指标,X1和X2的联合重要性指标即为d(X1) +d(X2)。

2.5 共性分析

另一种划分因变量方差的方法是共性分析(commonality analysis),与前文方法不同的是,它不假定解释的方差能够独立地分给每个自变量,而是存在着公共的方差解释部分。共性分析将解释的方差划分为两个部分,一个为独特效应,表示仅能够由某一自变量解释的方差;一个为共同效应,表示多个自变量共同解释的方差。如图4 所示,椭圆圈代表各变量的方差,阴影部分为Y被X1和X2解释的方差,也即X1和X2的联合贡献,它分为X1的独特贡献U1,X2的独特贡献U2,以及X1,X2的共同贡献C12。X1的单独贡献表示为U1+C12。自变量的独特效应U是自变量最后一个加入模型的R2增量,即前文提到的 ΔR2。图4中三部分效应分别为：

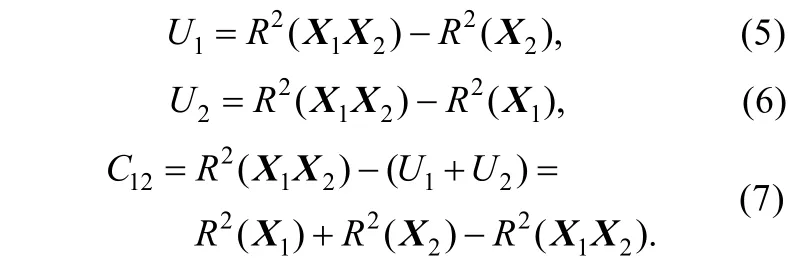
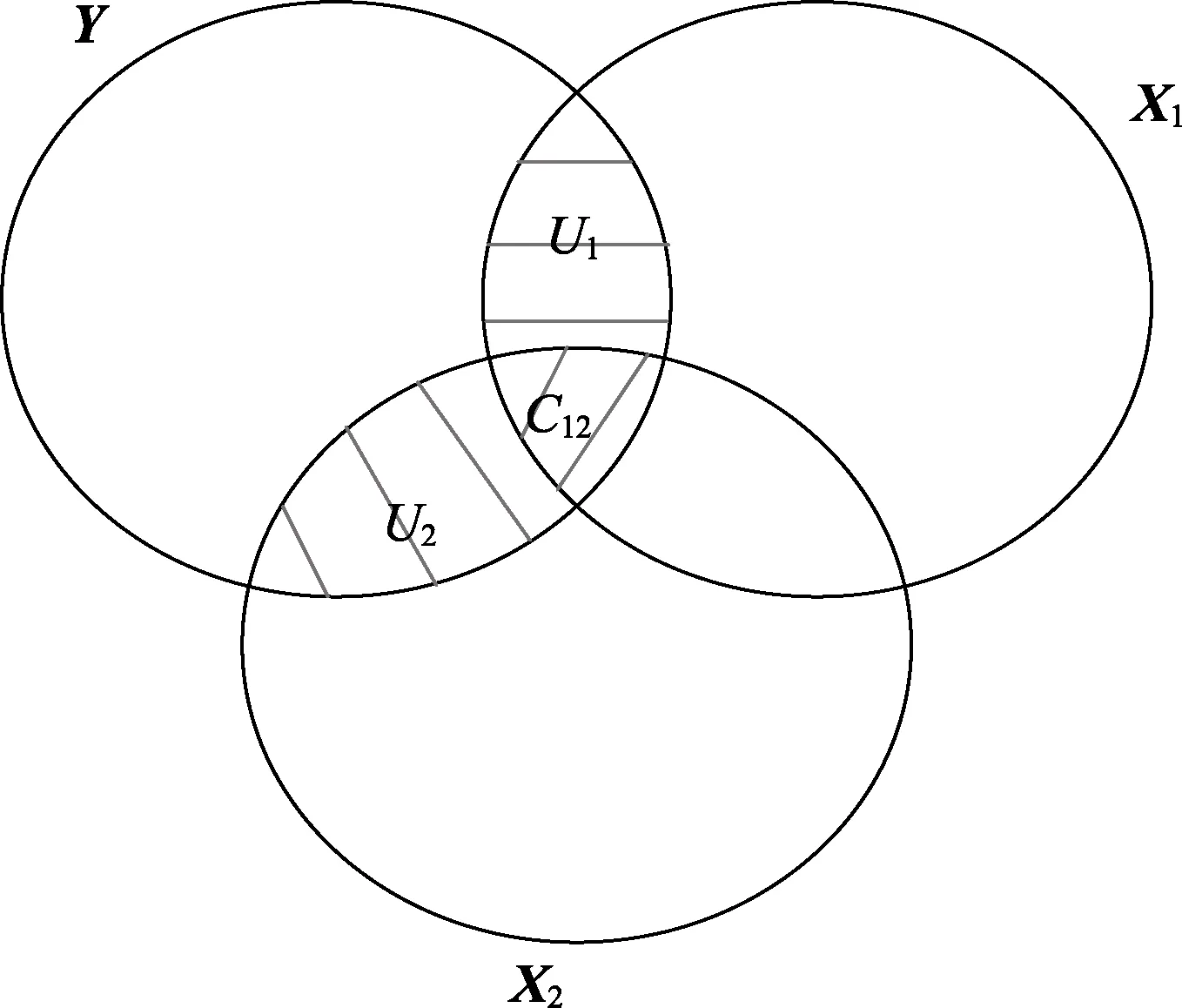
图4 共性分析

独特效应和共同效应统称为共性系数(commonality coefficient,简称CC)。当有多个自变量时,共性系数的计算公式可以通过多项式展开的方法得到。表3 列出了考试成绩回归模型的共性分析结果,所有共性系数之和为R2(Y) 。仅能由学科能力解释的方差占总方差76%,学科能力与复习时长共同解释的方差占总方差24%,这两部分解释了绝大多数的方差,可见学科能力对解释或预测考试成绩最重要。此外,复习时长的独特效应为 0,但和学科能力有较大的共同效应;焦虑程度的独特效应不为0,且与学科能力的共同效应为负数。由表3 可知,共性分析可能产生负的重要性估计值,Ozdemir (2015)对这一现象的解释为存在抑制变量(suppressor variable)。

表3 共性分析结果

共性分析能够解释变量间的关系,检测抑制变量,通过考量独特效应和共同效应综合评估自变量对因变量方差的贡献(Ozdemir,2015)。可能的问题是高阶共性和负共性很难解释。

2.6 相对权重分析

相对权重分析从不同的视角出发评估变量相对重要性。自变量相互独立时,各自变量标准化回归系数的平方和为R2,因此,相对权重方法的思想是寻找一组正交变量,使其与原始自变量具有最大相关,作为对原始自变量的近似。如果原始自变量相关程度不高,则正交变量的标准化回归系数的平方可近似作为原始自变量的相对重要性指标。但是如果原始自变量高度相关,则正交变量无法很好地近似原始自变量,其标准化回归系数的平方不能作为相对重要性指标。

对于考试成绩回归模型,w(学科能力)=0.57,w(复习时长)=0.08,w(焦虑程度)=0.01。

相对权重分析的步骤可总结为：(a)创建原始自变量的正交逼近;(b)获得原始自变量和正交变量的系数;(c)获得正交变量和因变量的系数;(d)结合两组系数。相对权重方法能够表示R2分解,能够衡量变量组重要性,w1+w2可以解释为X1和X2的联合重要性,更重要的是相对权重具有较高的计算效率。对该方法可能的批评是,如果采用不同的正交近似过程,所得到的结果可能有所差异。另外,Thomas 等人(2014)指出该方法在将正交变量解释的方差分配到原始自变量时使用的方法仍是基于相关系数的方法。

2.7 变量重要性指标的比较与选择

变量相对重要性各种指标的性质如表 4 所示。大部分的相对重要性指标是非负的,与相关系数和标准化回归系数有关的指标不能比较变量组。与R2增量有关的指标能够解释为对因变量方差解释的贡献且可以比较变量组。和wj等指标都能对R2进行分解。但是,乘积指标和共性分析系数CC都存在难以被解释的问题。不同进入次序的R2平均增量、Shapley 值和一般优势指标具有相同的评估结果。其中,优势分析对变量重要性的含义有直观的解释,且定义了相对重要性的不同模式,因此更具优势。不同进入次序的R2平均增量、Shapley 值、优势分析和共性分析都需要大量的计算。而相对权重分析提供了和一般优势分析几乎相同的评估结果,前者可以看作后者的近似,相对权重分析的优点是计算效率较高。

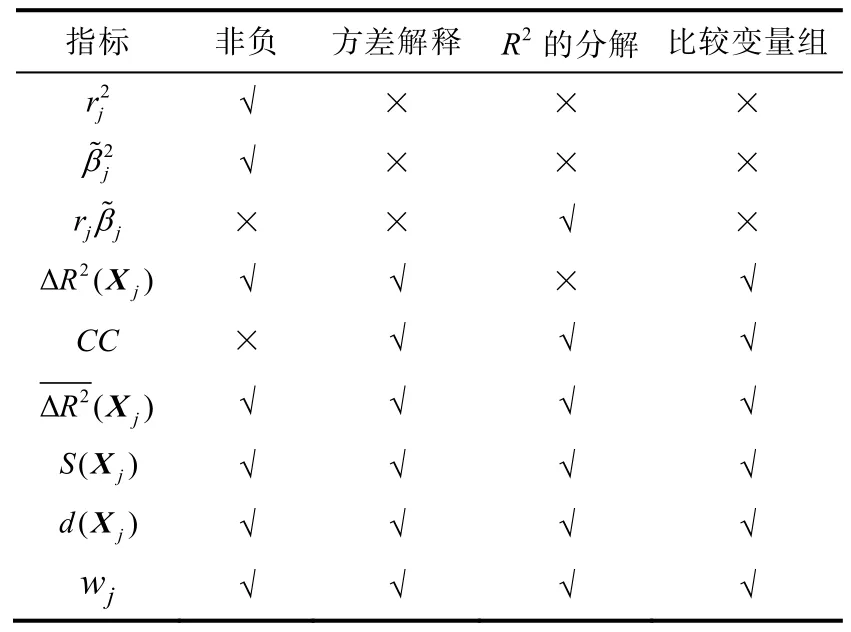
表4 相对重要性指标对比

根据以上讨论和实际研究问题,给出相对重要性指标的选择参考：首先,如果研究者只关注自变量对因变量的单独贡献,那么相关系数可以作为重要性评估指标;如果研究者只关注自变量对因变量的独特贡献,那么标准化回归系数可以作为重要性评估指标。但是,以上指标均不能比较变量组或分类变量的重要性。其次,如果研究者希望通过自变量对因变量的独特贡献和共同贡献来解释变量间的关系,可以使用共性分析。再次,如果研究者关注自变量对因变量方差解释的贡献,那么优势分析与相对权重是合适的重要性评估指标,综合考虑单独贡献和独特贡献,衡量每一个自变量对R2的贡献比例。根据表4 比较结果,本文重点推荐优势分析与相对权重指标。R2平均增量和Shapley 值的评估结果与优势分析相同,但优势分析更关注心理学意义的重要性解释。具体地,如果研究者更关注相对重要性的解释与模式,推荐使用优势分析;如果研究者希望评估大量自变量的相对重要性,则应选择相对权重指标。最后,值得注意的是,所有相对重要性指标都可直接由变量相关系数矩阵计算得到,不需要原始数据样本(Gu,2021)。

3 变量相对重要性的统计推断

本节讨论相对重要性的统计推断方法。使用第2 节中的考试成绩回归模型为例,说明不同相对重要性指标的频率统计与贝叶斯统计推断过程。生成样本容量为N=200,各变量均值为零,协方差矩阵为表1 所示的多元正态分布数据。为了便于解释,这里只生成一个数据集,并限制样本均值和协方差矩阵与总体中完全相等。

3.1 频率统计推断

传统相对重要性指标相关系数及标准化回归系数都服从t分布。以标准化回归系数为例,通过检验零假设,即可得到标准化回归系数的显著性。对模拟样本做回归分析,学科能力对应的=0.83,P＜0.001,复习时长对应的=0,P=1,焦虑程度对应的=-0 .17,P＜ 0.001,说明以标准化回归系数为重要性指标,学科能力和焦虑程度对考试成绩都有显著的重要性。如果想要知道两个自变量的标准化回归系数是否有显著差异,则可使用Wald 检验判断系数的差异显著性H0:-=0。但是,对于三个变量相对重要性的推断,多重Wald 检验即便可能,统计功效也会十分低下(Braeken et al.,2015)。

一般优势分析和相对权重等指标的抽样分布函数未知,可以使用bootstrap 抽样方法构造的抽样分布来替代。这里以一般优势分析为例,对于大小为N的样本,重抽样得到S个bootstrap 样本,在每个bootstrap 样本中计算一般优势指标,就得到了指标的抽样分布。模拟样本中一般优势指标的bootstrap 抽样分布如图5 所示。

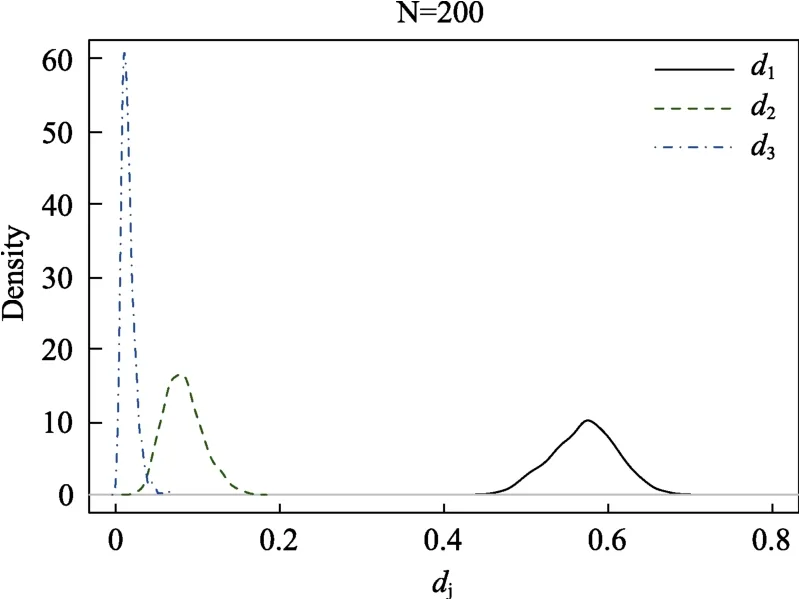
图5 一般优势指标的bootstrap 抽样分布

根据抽样分布即可计算优势指标或指标差异的标准误、置信区间等。Bootstrap 提供了百分位置信区间和BCa (bias-corrected and accelerated)置信区间,95%置信区间的下限和上限分别是bootstrap 抽样的2.5%和97.5%分位数,BCa 置信区间用偏差校正加速方法对百分位置信区间进行调整,得到更精确的结果。根据估计值和标准误可以构造Wald 统计量,并计算其显著性。由于一般优势指标总是非负的,因此对该指标的显著性计算是单边的。以模拟样本为例,学科能力的一般优势指标1d估计值为 0.57,标准误为 0.04,bootstrap 百分位置信区间为[0.49,0.65],BCa 置信区间为[0.49,0.65],Wald 统计量为14.36,P 值小于0.001,因此学科能力的一般优势指标显著不为0。学科能力和复习时长一般优势指标差异d1-d2的估计值为0.49,标准误为0.06,bootstrap 百分位置信区间为[0.37,0.59],BCa 置信区间为[0.37,0.60],Wald 统计量为8.79,P 值小于0.001,可知学科能力的一般优势指标显著大于复习时长,也即在解释或预测考试成绩上,学科能力比复习时长重要。Wald 检验和bootstrap 方法只能推断两个自变量的相对重要性次序。在涉及三个及以上的比较时,仍然需要多重检验。

变量重要性指标估计值的大小次序在bootstrap样本中出现的频率称为相对重要性次序的复现性。以一般优势指标为例,模拟样本中的估计值为,重要性次序d1＞d2＞d3。进行1000 次bootstrap 抽样,并分别计算一般优势指标,其中980 个bootstrap 样本中满足d1＞d2＞d3,则重要性次序的复现性为98%。

3.2 贝叶斯统计推断

涉及变量相对重要性的心理学理论可以由次序假设表示。例如,H1:d1＞d2＞d3表示在解释或预测考试成绩时,三个自变量在一般优势指标下的重要性由高到低依次为学科能力、复习时长和焦虑程度。贝叶斯检验可以直接评估次序假设,贝叶斯因子是贝叶斯检验的核心指标。与传统方法相比,贝叶斯检验有以下一些优势(Hoijtink et al.,2019)：贝叶斯检验能够接受零假设而显著性检验不能;贝叶斯因子量化了数据支持假设的证据;贝叶斯因子能够同时检验两个及以上可能的次序假设,不需要考虑多重检验修正;此外,贝叶斯因子能够随着数据的不断收集而更新。

贝叶斯因子为数据在两个假设下的边际似然比值(marginal likelihood ratio)。由于零假设或次序假设都嵌套于无约束的备择假设,零假设与备择假设的贝叶斯因子可简化为待检验指标在零假设下的后验与先验密度的比值,次序假设与备择假设的贝叶斯因子可简化为待检验指标在次序假设限定下的后验与先验概率的比值。贝叶斯因子的简化表达被称为Savage-Dickey 密度比或概率比(Mulder et al.,2022)。先验密度或先验概率可由设置的指标先验分布直接计算,如正态先验在指标为0 时的密度即为先验密度。后验密度或后验概率可借助后验抽样进行估计,如后验样本服从次序假设的比例即为后验概率。零假设或次序假设的贝叶斯因子计算可利用R 软件包bain,更多的理论细节参见Gu 等人(2018)和Gu (2021)。贝叶斯因子对数据证据的衡量标准参见表5(胡传鹏等,2018)。三个及以上假设的比较可将贝叶斯因子转换为后验模型概率。

表5 贝叶斯因子标准

以标准化回归系数为例,贝叶斯因子不仅可以检验单个变量重要性的显著性及两个变量重要性差异的显著性,还能评估包含更多信息的次序假设,如。以模拟样本为例,与备择假设Hu相比,对应的BF1u=8.17 ＞ 3表示接受H1,复习时长的标准化回归系数不显著;对应的表示拒绝H2,学科能力和复习时长的标准化回归系数有显著差异;对应的BF3u=4.14 ＞3 表示接受H3,三个自变量在标准化回归系数下的重要性次序为学科能力、焦虑程度和复习时长。

一般优势指标同样可以用贝叶斯方法检验。例如,我们认为学科能力对解释或预测考试成绩毫无疑问最为重要,而不确定复习时长比焦虑程度重要还是二者有相等的重要性,考虑相互竞争的两个假设：

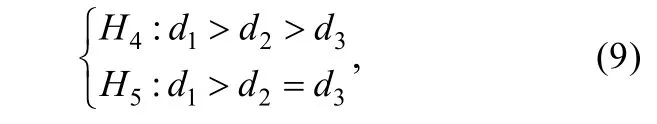
计算可得,BF4u=8.63,BF5u=0.92,BF45=BF4u/BF5u=9.44表明假设H4比H5受到的数据支持更多。

根据频率与贝叶斯统计推断的论述与比较可知,bootstrap 抽样方法原理简单,适用于各种指标下的单变量重要性和两变量重要性差异的推断。但是涉及三个及以上变量的重要性比较时,bootstrap 方法仅能给出重要性次序的复现性,无法进行统计检验。与此相对,贝叶斯方法能够检验重要性次序的任意假设,为相对重要性评估提供了直接、有效的方法。但是贝叶斯方法的统计原理和计算较为复杂,在相对重要性研究中的应用还不如bootstrap 方法广泛。

4 变量相对重要性的模型应用

基于标准化回归系数的变量相对重要性评估可直接拓展到多因变量回归模型、Logistic 回归模型、结构方程模型等。只需在各模型中估计出标准化系数及其标准误,就可以对变量重要性进行排序以及统计推断,分析过程与回归模型标准化系数的估计、排序与推断类似,这里不再赘述。下面主要讨论优势分析和相对权重方法在各类模型中的应用。

将优势分析拓展到其他模型的关键是选择合适的方差解释效应量R2(Azen & Budescu,2006)。R2与模型拟合有关,应满足：(a)有界性：R2在0到1 之间,0 表示完全缺乏拟合,1 表示完美的拟合;(b)线性不变性：R2对于非奇异的变量转换是不变的;(c)单调性：在模型中增加一个自变量,R2不应该减少;(d)可解释性：R2直观上易于理解。确定了R2后,自变量对特定模型的独特贡献就可以由自变量加入模型时的R2增量得到。Azen 和Budescu (2006) 使用基于典型相关(canonical correlation)的多元关联测量(multivariate association measure)作为多元R2,将一般优势分析指标拓展到多因变量回归模型。Logistic 回归模型适用于二分类因变量的情况,Azen 和Traxel (2009)使用基于似然比的R2对自变量进行优势分析。Luo 和Azen (2013)将优势分析应用于多水平模型。多水平模型R2效应量测量的综合框架参见Rights 和Sterba (2019),研究者可根据感兴趣的水平层次选取恰当的R2,评估不同水平下自变量的相对重要性。结构方程模型可以分析潜变量间的关系,Gu (2022)将优势分析方法拓展到结构方程模型,通过模型隐含相关矩阵(model-implied correlation matrix)计算潜变量回归模型的R2,得到优势分析指标。

相对权重分析拓展到其他模型的关键是设计正交过程以及合适地估计系数。对于多因变量的线性回归模型,直接估计系数不能考虑因变量的内在相关性,LeBreton 和Tonidandel (2008)同样创建因变量的正交逼近,作为正交变量和因变量之间的过渡。对于Logistic 回归模型,最小二乘框架不再适用,Tonidandel 和LeBreton (2009)使用标准化Logistic 回归系数作为正交变量与因变量的系数。在以上模型中,相对权重与优势分析表现出一致性。相对权重方法也被扩展到了包含交互项、二次项或其他高阶项的回归模型中以评估这些效应的相对重要性(Tonidandel & LeBreton,2011)。

相对重要性的应用已从线性回归模型拓展到二分Logistic 回归模型、多因变量回归模型、多水平模型、潜变量回归模型等,但是还未见有广义线性混合模型和结构方程模型这两大类模型的系统应用。例如,中介模型是心理学研究中广泛应用的模型,评估不同中介变量重要性的常用方法是比较各中介变量的特定间接效应(specific indirect effect),中介变量的特定间接效应可以用该变量所在路径的系数乘积来衡量(Preacher & Hayes,2008;Preacher & Kelley,2011)。计算特定间接效应之后,可使用bootstrap 方法构建两个中介变量特定间接效应差值(contrast)的bootstrap 百分位和偏差校正置信区间进行推断,若置信区间不包括0,则表明两个特定间接效应有显著的差异(Preacher & Hayes,2008;方杰 等,2014)。多重中介效应的比较与推断可在Mplus 和R 软件包lavaan 等结构方程模型软件中实现。但是,在相对重要性评估中,多重中介变量的间接效应指标存在与回归模型中标准化系数指标相同的问题,即某一中介变量的重要性可能被其他中介变量隐藏。而回归模型中评估自变量重要性推荐的优势分析和相对权重方法并未拓展到多重中介模型,可能的原因是多重中介模型涉及的路径较回归模型更为复杂,模型R2的解释、计算和分解较为困难。此外,已有的模型应用研究均未关注分类自变量的情形,相对重要性评估应用到分类数据时的稳健性还有待探讨。

5 变量相对重要性的心理学研究应用

近年来,为了推广相对重要性方法的实际应用,研究者在SPSS、Stata、SAS、R 等多个平台下开发了各种相对重要性指标计算和统计推断的相关软件(Kraha et al.,2012;Luchman,2021;Groemping & Matthias,2021;Mulder et al.,2021)。其中R 软件包提供了全面、灵活的分析工具,R 包dominanceanalysis 可以对线性回归模型(单因变量和多因变量)、广义线性模型以及多水平线性模型进行优势分析并计算bootstrap 复现性;R 包yhat可以在线性回归模型中实现优势分析和相对权重方法并计算bootstrap 置信区间(Nimon & Oswald,2013);R 包bain 可以利用相对重要性指标的估计值和协方差矩阵计算一般统计模型下任意重要性指标的零假设和次序假设的贝叶斯因子,进行多变量重要性排序的统计推断(Gu et al.,2018)。

随着相对重要性方法的研究发展与软件实现,相对重要性评估广泛应用于心理学研究中。许多研究者使用优势分析和相对权重方法从因变量方差贡献比例的角度比较变量的相对重要性(Casillas et al.,2012;Hakanen et al.,2021;Richardson et al.,2021;Modersitzki et al.,2021)。例如Casillas 等人(2012)使用优势分析比较了社会心理和行为因素(如动机、自我调节和社会控制)及先前学业成就对高中生学业成绩的重要性。Modersitzki 等人(2021)使用相对权重比较了新冠疫情下社会人口变量和人格特征变量(包括大五人格、黑暗人格等)对预测心理结果的相对贡献。相对权重方法因其在计算效率上的优势,更适用于自变量较多的模型,也有许多元分析使用这种方法来评估相对重要性(Young et al.,2018;MacCann et al.,2020)。例如,Young 等人(2018)的一项元分析使用相对权重确定不同人格特质在预测员工敬业度中的相对重要性。

国内使用相对重要性方法的心理学研究也有不少,主要集中在心理健康、教育心理和组织研究领域(周浩,龙立荣,2014;宋勃东 等,2015;张纯霞,冯廷勇,2018;胥彦,李超平,2019;Zhang et al.,2021;胡咏梅,元静,2021)。例如张纯霞和冯廷勇(2018)使用优势分析比较了冲动性各维度对学习拖延行为的相对贡献。胥彦和李超平(2019)的一项元分析使用相对权重比较了不同领导风格对员工敬业度的解释力。胡咏梅和元静(2021)使用Shapley 值,比较了家庭投入和学校投入对于中小学教育产出的重要性。

除了相对重要性的描述性评估,部分心理学研究关注重要性的统计推断(Vaessen & Blomert,2010;Dalal et al.,2012;Ainsworth & Oldfield,2019)。例如Vaessen 和Blomert (2010)使用优势分析指标的置信区间进行统计推断,比较不同年级的语音意识和快速自动命名对阅读流利性的贡献。Ainsworth 和Oldfield (2019)使用相对权重方法比较了促进教师韧性的各种因素在预测工作满意度、倦怠和幸福感中的相对重要性并使用置信区间推断显著性。

对应用文献进行分析,发现相对重要性的应用研究存在以下几点问题：(1)不恰当的指标使用与解释,前文提到重要性的评估指标有不同解释,应根据具体研究问题确定。(2)应用模型大多为线性回归,可能的原因是其他模型下的相对重要性评估方法开发主要集中在近10 年,比如多水平模型与结构方程模型的变量重要性评估的方法研究与软件开发还未完善。(3)重要性评估报告主要为描述性的,尤其是多变量的排序,忽略了统计推断信息(Braun et al.,2019)。(4)缺乏综述类文献的指导,近二十年来,相对重要性领域出现了很多新发展与新模型,而心理学领域缺乏相关的综述文章指导。

6 变量相对重要性的应用实例

本节以观看芝麻街儿童电视节目(Sesame)的一项研究为例(Stevens,2002)说明一般优势分析的实际应用。研究者试图探究儿童数字知识的影响因素。该研究数据可见R 包bain 中的“sesamesim”数据集,它包括240 名34 到69 个月的儿童。因变量为Postnumb,是观看芝麻街节目一年后儿童的数字知识测验得分。自变量为儿童观看节目前的数字知识得分Prenumb、年龄Age以及Peabody心理年龄得分Peabody。它们的关系可以用线性回归模型表示：

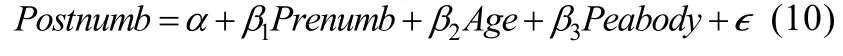
表6 展示了因变量和自变量的相关矩阵和自变量标准化回归系数的估计值。

表6 相关系数与标准化回归系数估计值

根据表6 的相关矩阵计算各自变量的一般优势指标,并通过 bootstrap 抽样得到标准误、bootstrap 百分位置信区间和BCa 置信区间以及Wald 检验结果,如表7 所示。Wald 检验结果表明三个自变量在预测因变量上的重要性都是显著的。

表7 一般优势指标、标准误、置信区间和Wald 检验

研究者可根据心理学理论构建并检验特定的自变量重要性排序,同时也可以对所有重要性次序进行探索与评估,这里为探索自变量的重要性次序,评估以下假设：

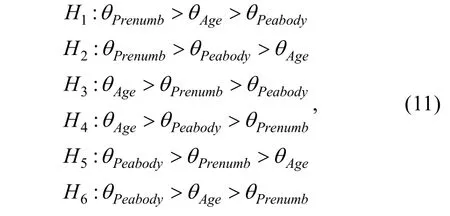
其中θ表示重要性指标。以标准化回归系数和一般优势指标为例,表8 展示了上述假设的贝叶斯统计推断结果,包括每个假设的贝叶斯因子。对于标准化回归系数,与备择假设Hu相比,BF1u=0.44表示数据不支持也不反对H1,BF2u=5.77表明H2得到数据的支持。对于一般优势指标,BF2u=5.54表明数据支持H2;其他假设的贝叶斯因子都小于1/3,表明数据更支持备择假设Hu。在所有考虑的假设中,H2的贝叶斯因子BF2u最大,表明其得到了最多的数据支持。标准化回归系数和一般优势指标的贝叶斯检验给出了同样的结果,也即在预测观看芝麻街后的数字知识测验得分上,观看前的数字知识最重要,Peabody 心理年龄的重要性次之,而年龄的重要性最小。

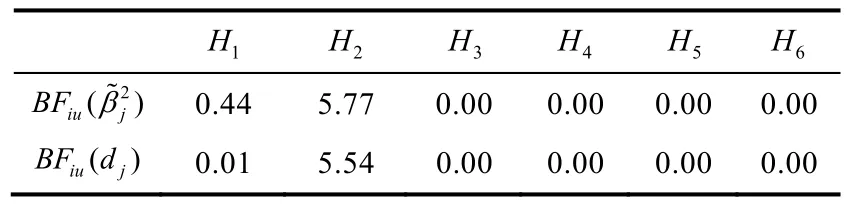
表8 贝叶斯统计推断

7 总结与展望

变量相对重要性的研究对心理学、教育学等社会科学有重要意义。尽管目前的研究中习惯于使用标准化回归系数等传统指标来比较变量的重要性,在自变量相关时,这些指标不能同时考虑自变量对因变量的直接影响和控制其他自变量后的影响。不同进入次序R2增量的平均值、Shapley值、优势分析和相对权重等给出了变量相对重要性的统一评估指标,得到几乎相同的分析结果。优势分析与相对权重指标同时考虑自变量对因变量的单独和独特贡献,对R2进行分解,并能够衡量分类变量和变量组的重要性,是比较推荐的指标。更具体地,当研究关注的重点是重要性分析的不同模式时,更推荐优势分析;当自变量个数较多时,更推荐使用相对权重方法。由于优势分析与相对权重指标的抽样分布往往是未知的,bootstrap 置信区间是推荐的统计推断工具。当比较三个及以上自变量的相对重要性时,更推荐使用基于贝叶斯因子的统计推断方法评估多自变量的重要性次序。

变量相对重要性的研究仍然存在很多值得探索的地方。首先,优势分析和相对权重方法的模型应用仍较为有限,没有系统地应用在广义线性混合模型、结构方程模型中。如前文所述,在多重中介模型中比较不同中介变量的重要性时,目前常用的基于系数乘积的特定间接效应比较方法可能导致对某些中介变量重要性的低估。中介效应同样可以使用R2度量,可以理解为由自变量和中介变量共同解释的因变量的方差(Lachowicz et al.,2018),将优势分析和相对权重方法拓展到中介变量的相对重要性评估是未来的一个研究方向。

其次,尽管优势分析和相对权重分析是当前最为推荐的相对重要性评估方法,它们都有各自的不足。优势分析要对所有可能的子集计算R2增量,因而当变量较多时计算效率较低。基于一般优势分析对R2分解的性质,可能的改进思路是对大量变量进行分组降维、并行计算。此外,在一些较为复杂的模型中,R2的选择和计算较为困难。例如多水平模型中有很多不同的R2(Rights & Sterba,2019),研究者需要选取恰当的R2进行优势分析。建议优势分析方法研究能给出这类模型的具体应用指南。相对权重方法因其与一般优势分析相似的结果及较高的计算效率而被广泛使用,但是该方法在将正交变量解释的方差分配到原始自变量时使用的方法仍是基于相关系数的方法,从而可能导致解释方差不恰当的划分。相对权重方法如果要拓展到更广泛的模型,须解决这个问题。

再次,实际分析中不同数据类型的变量重要性指标估计与推断的稳健性还有待探讨。例如,心理学研究常使用李克特量表测量研究变量,为了满足回归模型的基本要求,可能假定量表得分服从正态分布。违背正态性假定会对相对重要性评估产生怎样的影响是值得研究的问题。又如,心理学研究常涉及分类变量,同一分类自变量(如受教育水平)类别划分较多时(如研究生、本科、专科、高中、初中及以下)与类别较少时(如专科及以上、高中及以下)对R2的贡献有何不同,即分类自变量的相对重要性评估是否会受到类别数量的影响也是值得进一步探讨的问题。因此,相对重要性评估的稳健性模拟研究是未来研究的一个方向。最后,相对重要性评估缺乏集成的分析软件,同时执行评估指标的计算与统计推断。因此,未来相对重要性评估方法研究应更关注模型的应用、数据的适用与软件的开发。