面向高通量的多通道复用数字全息成像技术
黄郑重,曹良才
(清华大学 精密仪器系 精密测试技术及仪器国家重点实验室, 北京 100084)
1 引 言
准确探测光波在空间中的分布对于研究物体与波之间的相互作用至关重要。从1948年Dennis Gabor首次提出全息术至今[1],已走过70余年的岁月。时至今日,全息术已成为一种成熟的定量相位测量手段,利用已知参考光与未知物光相干涉,用像感器记录对应的干涉图,利用计算机的数值重建方法实现原始物体光振幅和相位信息的重建。在生物样本分析、材料表征、物质结构分析等领域有着重要应用。
相位信息主要体现为物体内部与外部环境的光程差,比如生物样本通常是无色透明的,它对光的吸收值较低,因此采用传统的明场成像方法获得的图像衬度非常低。但由于细胞内部细胞液与外部介质的折射率存在差异,其主要信息可反映在光的相位中。对于光学波段而言,现有的商业相机难以直接探测相位,仅可以记录下来光强信息。通过化学染色、荧光染色等方法可以提升其强度对比度,但标记过程中需要提前制备样本,对细胞的正常生理活动可能带来不利影响[2-3]。
无标记显微术是一种理想的、可探测活细胞动态过程的手段。根据提取相位信息的技术手段不同,无标记显微术可分为以相位观测为目的的定性成像和以精确量化为目的的定量成像。1942年,泽尼克提出了相衬成像方法(Zernike Phase Contrast, ZPC)[4],提高了对无标记细胞样本的相位成像对比度,并因此于1953年获得了诺贝尔奖。此后,微分干涉相衬成像(Differential Interference Contrast, DIC)[5]的提出进一步促进了相衬成像的发展,其与ZPC方法成为生命科学领域广泛使用的相衬观察技术。然而相衬最终获得的图像强度与相位分布不呈线性关系,仅提升了透明物体的对比度,这限制了后续的定量分析。定量相位成像(Quantitative Phase Imaging,QPI)是以精确量化光场相位为目的的成像技术。近年来,随着计算机和探测器的发展,一系列基于强度图反演相位的计算成像方法被提出, 如基于迭代计算的相干衍射成像(Coherent Diffraction Imaging,CDI)[6-7]、基于傍轴近似直接计算的强度传输方程(Transport of Intensity Equation,TIE)[8-10]、基于叠层迭代的衍射成像算法(Ptychography)[11-17]、基于单边带信号强度的希尔伯特变换算法[18-20]等。在上述方法中,相位恢复的本质是数学上的反问题求解。此外,基于干涉的成像方法可以提供确定的相位解[21],无需借助先验假设且具有数学完备性。数字全息是其中具有代表性的技术,其可进一步分为同轴全息和离轴全息。同轴全息中物光和参考光沿相同方向传播,可使物光充分利用相机的空间带宽。在同轴全息中,通常采用相移干涉方法,在物光和参考光之间依次引入多个不同相移量[22-25],来实现对原始光场复振幅信息的高精度和非接触测量。该方法由于需要多帧数据合成,不可避免牺牲成像时间或成像视场,此外,精确的相移量调制还会增加系统成本。离轴全息通过引入离轴参考光与物光干涉[26-27],可以在频域上将物光谱和其共轭谱完全分离,实现单帧定量相位重构,具有实时成像的能力。但为了满足此分离条件,重构出的再现像分辨率一般要大于8个像素,远低于相机的采样频率,因此限制了单帧图像可重构的信息量和空间带宽积[28]。
实现更高通量是光学成像技术一直追求的目标,尤其是随着生命科学和材料科学向着微纳尺度发展,大视场高分辨成像技术的重要性愈发突出。一个光学系统成像的信息通量可由空间带宽积(Space-Bandwidth Product, SBP)描述[29],它是指一个光学成像系统在其成像视场内光学可分辨点的数量。它是一个无量纲的物理量,可以用视场范围和最小可分辨特征尺寸,即分辨率,计算得到。最终成像结果的视场越大、可分辨特征越小,则系统的空间带宽积越高,测量结果中所包含的信息量就越多。随着光学设计和加工技术的进步,传统光学成像系统的信息通量逐渐提高。为了突破探测器或计算能力对成像通量的限制,研究人员提出了一系列基于计算照明、计算调制和计算探测等提升成像通量的方法。这些方法大体上可分为两种:空间域拓展和频域拓展。
本文基于数字全息成像技术,从高通量成像系统的实现手段出发,梳理了基于空间域和频域拓展的成像方法,介绍了多通道数字全息复用技术的产生与应用,并介绍了高通量数字全息复用的求解框架,最后对高通量数字全息技术的应用进行了展望。
2 高通量成像基本思路
对于一个相干成像系统,以传统显微镜的圆形光瞳为例,定义其空间带宽积为[29]:

其中D为成像视场的直径,M为放大倍率,NA为系统的数值孔径,λ为照明波长。可见,在光源和放大倍率确定的情况下,重构信息通量主要受视场和数值孔径NA的限制。从SBP的定义来看,拓展成像通量的方法大体上可分为空间域拓展和频域拓展。成像系统空间带宽积空间域拓展的基本思想是在保持成像系统的分辨能力不降低的情况下,增大成像视场,获取更广的空间域信息,实现“看得更广”的目的。如图1(a)(彩图见期刊电子版)所示,可通过相机或样本的平移扫描,获取更多样本信息。该方法要求系统稳定性高,扫描方向与样品平面之间需严格平行,对于大尺度静态样本的观察具有显著优势,在全玻片病理成像方面已经得到了应用[30-34]。相对于单相机扫描,多相机阵列的空间排布可直接覆盖大成像视场范围,通过并行采集的方式可保持单帧成像的特性。在传统镜头设计中,大视场成像易受到离轴场曲的影响,随着透镜尺度的增加,该影响逐渐增大。2012年,杜克大学的Brady等人展示了基于主副透镜的多尺度相机阵列成像系统[35-37],该系统结构和成像结果如图1(b)(彩图见期刊电子版)所示。该模型利用大型主透镜和多个小透镜阵列解决了离轴像差问题。物体经大型主透镜产生弯曲的中继焦面,该中继面由各次级小透镜阵列移动到对应的焦点进行物理补偿,生成的图像经过物理组合后再现大视场成像结果。该方法的优势在于设计主镜头时可以容忍更大的场曲,从而放宽对大口径光学器件设计的要求。
2019年,清华大学Fan等人[38]使用多尺度显微镜系统展示了厘米视场和微米分辨率下生物动力学的视频成像,如图1(c)(彩图见期刊电子版)所示。系统的定制主物镜工作距离为 20 mm ,可对大视场的荧光场景进行成像。中间焦面图像由设置在其曲面分布的次级透镜进行分割和中继。单帧图像由传感器阵列测量,并展示了癫痫神经活动中的钙非均匀传播成像。由此可见,空间域拓展的基本方法可通过更多像素点采集场景信息并拼接成高分辨率图像,具有实际应用价值。
与空间域拼接拓展信息量相比,频域拓展方法的基本思想是拓展成像系统所能收集的频域信息,旨在有限成像视场中提升光学分辨率,实现“看得更细”的目的。根据傅立叶变换特性,傅立叶域(频域)中的平移位移对应于真实空间中的角位移,如图1(d)(彩图见期刊电子版)所示。对应样本的各空间频率分量可以通过不同角度照明获得,最终在频谱域合成拓展的高频信息。2013年,美国加州理工学院Yang和Zheng等人提出了傅立叶叠层成像[13,39-40],是频域合成领域具有代表性的计算成像技术。该技术依次改变照明光角度,基于傅立叶平移特性,实质上是使成像样品的频谱通带在频域中进行平移。在空间域中,将拍摄到的不同照明角度对应的光强图作为解的振幅约束,将频域中受限的传递函数作为解的支撑约束,通过大量的照明角度扫描,利用相位恢复算法在空间域和频域中交替迭代投影,最终在不牺牲成像视场的情况下实现成像频域通带的拓展,提升成像系统的等效数值孔径(NA),重建得到了样品的高分辨信息,如图1(e)(彩图见期刊电子版)所示。基于低NA显微物镜的大视场特征,在频域中迭代拼接高频分量,可以获得高分辨、大视场的定量相位成像结果。2014年,美国加州大学洛杉矶分校Ozcan等人提出合成孔径片上显微成像技术[41-42],将频域叠层方法引入无透镜成像系统中,如图1(f)(彩图见期刊电子版)所示,与基于透镜的傅立叶叠层技术类似,通过不同照明角度在频域中的通带位移映射关系,采集不同照明角度下的光强图,并利用相位恢复算法在空间域和频域中交替迭代投影。与透镜系统不同的是,由于片上显微系统数值孔径接近1,此时系统分辨率受限于像素尺寸,并且传感器探测的不是聚焦图像,因此需要加入像素超分辨和光场自由空间传播的过程。该方法的本质还是基于交替投影的相位恢复迭代过程。这里需要注意的是,频域子孔径间的交叠率必须足够大,需要一定的数据冗余量,才能使最终迭代收敛并准确重构高分辨的复振幅信息。因此频域拓展是通过采集不同照明方向对应的强度图,使合成图像的频谱拓展至超出光学成像系统传递函数的范围。

图1 成像空间带宽积拓展。(a)空间域拓展示意,拓展光学系统的空间域成像范围;(b)基于相机阵列的多尺度光学成像系统[36-37];(c)基于相机阵列的大视场生物显微成像系统[38];(d)频域拓展示意,拓展现有光学系统的频率通带范围;(e)基于多角度照明的傅立叶域叠层显微成像系统[40];(f)基于多角度照明的无透镜片上成像系统[41]。Fig. 1 The expansion of the imaging SBP. (a) Schematic diagram of the expansion in spatial domain to expand the spatial imaging range; (b) the multi-scale optical imaging system based on the camera array[36-37]; (c) the large field of view biological microscopic system based on the camera array[38]; (d) schematic diagram of frequency domain expansion, expanding the frequency passband range of existing optical systems; (e) fourier ptychographic microscopy system based on multi-angle illumination[40]; (f) lensless on-chip imaging systems based on multi-angle illumination[41]
3 全息复用技术
3.1 数字全息
数字全息技术是实现定量相位成像的有力工具,利用光学干涉原理,通过引入参考光将物光波前“冻结”在干涉条纹中并由传感器记录,仅通过采集单幅全息图即可完整再现样品的振幅和相位信息。在离轴全息中,倾斜参考光使物光波和共轭波在全息图的频域上完全分离,通过滤波方法可直接从强度图中重建物光波[26-27],其原理如图2(彩图见期刊电子版)所示。相较于傅立叶叠层成像,基于离轴数字全息的相干合成孔径可以实现非迭代、实时的频域拓展[43-44]。原理与傅立叶叠层成像技术类似,在相干光照明下,采集不同照明角度下的光强图。核心在于利用离轴全息技术,可直接从强度图的频谱中把对应的物体频域通带部分提取出来,遍历不同角度并获得对应的频率分量,直接在频域空间叠加后进行逆傅立叶变换,即可得到准确的高分辨复振幅重构信息,无需迭代耗时,并且对子孔径间的交叠率没有苛刻要求。
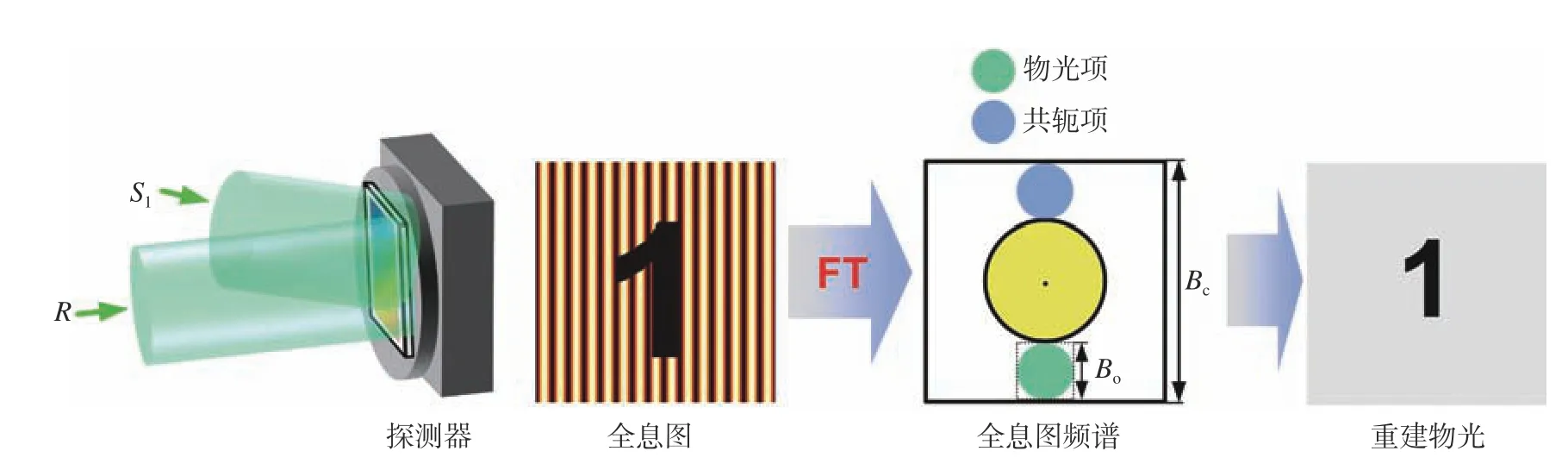
图2 传统离轴数字全息示意图,FT为傅里叶变换(Fourier transform)的简称Fig. 2 Schematic diagram of conventional off-axis digital holography. FT indicates the Fourier transform
3.2 数字全息复用
实现高通量成像的一种思路是通过海量的数据采集,利用数据冗余和计算算法合成一幅具有高空间带宽积的图像。此外,提升采集数据的利用效率也是实现高通量成像的有效途径,在实现高通量成像的前提下,降低对源数据冗余量的要求,可提升采集效率。数字全息复用技术通过引入多路物光与参考光相干涉,进一步利用离轴全息频谱中的冗余部分,在不牺牲时间带宽积的前提下,提升了单帧离轴强度图的可重建信息量。全息图的空间带宽利用率定义为物光项和共轭项所占全息图总频谱的面积比值[45]。从图2的频谱图可知,在传统离轴全息中,物光频谱仅占整个全息图频谱的一小部分。对数字全息图进行傅立叶变换,其频谱的横向总带宽Bc=1/Δ,Δ是像素尺寸。物光波总带宽为Bo,在透镜成像系统中,其频谱形状为圆形,其半径由系统的数值孔径、放大率和照明波长决定,如图2中的频谱图绿色项所示。零级项包含了物函数的自相关项,其宽度为物光频谱的两倍。由于物光项与其他项完全分离,其总带宽应小于全息图带宽的1/4。假设物光频谱半径为相机带宽Bc的1/8,则物光项的频域面积为 π[1/(8Δ)]2,并且共轭项的频域面积与其相等,而总频域面积为 (1/Δ)2。此时传统全息图的空间带宽利用率仅为9.82%[45]。图3(a)(彩图见期刊电子版)展示了双通道复用示意图,两路物光波前携带了不同的复振幅信息,并且分布在全息图频谱中的不同位置。在Bo=0.25Bc的情况下,物光项与共轭项的面积较图2的传统离轴全息情况增大一倍,其空间带宽利用率为19.63%[45-46]。进一步,引入更多的物光分布在空余的频谱内,全息图中心频谱为零级,物光谱分布在零级周围。在Bo=0.25Bc的情况下,最高可以引入6路物光复用至同一全息图中,此时全息图的空间带宽利用率为58.9%[45]。
如图3(b)(彩图见期刊电子版)所示,多路物光可包含多视场的信息[47-48],最终重构视场超相机视场2倍左右,实现了空间域拓展;其还可包含多空间频率信息[49],如图3(c)(彩图见期刊电子版)所示,六路物光携带了样品不同方向的高频成分,通过频域滤波组合形成频域拓展的高分辨成像,实现了频域拓展;还可包含三维信息,如图3(d)(彩图见期刊电子版)所示,多路物光携带了样品不同层的信息[50],通过频域滤波组合形成三维样品的层析成像。值得注意的是,与图1展示的通过海量数据采集实现空间域或频域拓展不同,复用技术提升了强度图携带的信息量,从单帧强度图中实现重构信息量拓展,并且无需迭代过程。

图3 数字全息复用技术及其应用示意图。(a)双通道离轴全息复用示意图;(b)基于复用技术拓展成像视场[47];(c)基于复用技术拓展成像分辨率[49];(d)基于复用技术拓展成像深度[50]Fig. 3 Schematic diagram of digital holographic multiplexing and its applications. (a) Schematic diagram of dual-channel offaxis holographic multiplexing; (b) expanding imaging field of view based on digital holographic multiplexing[47];(c) expanding imaging resolution based on digital holographic multiplexing[49]; (d) expanding imaging depth of field based on digital holographic multiplexing[50]
4 面向高通量的数字全息复用技术
4.1 基于希尔伯特变换的高通量数字全息复用
在传统离轴全息中,物光与参考光会在探测器平面上形成干涉强度图,其将与主光线方向形成一定的夹角。倾斜参考光使物光波和共轭波在全息图的频域上完全分离,通过滤波方法可直接从强度图中重建物光波。多路复用通过引入多路物光与参考光相干涉,此处以两路复用为例,其全息图的强度表达式为:
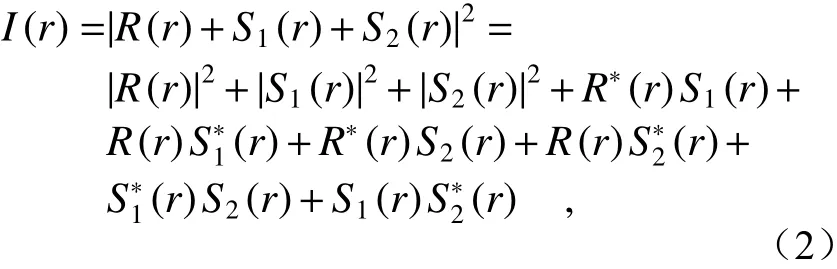
其中R(r)为 参考光函数,S1(r)和S2(r)分别为两路物光函数。在式(2)中,前3项为两路物光和参考光的模平方,即在频谱上表达为零级项;第4项和第5项包含第一路物光的频谱及其共轭谱;第6项和第7项包含第二路物光的频谱及其共轭谱;第8项和第9项包含物光之间的互相关谱。为了简化讨论,物光之间的互相关谱未在图3(a)中展示。其中,零级谱恒定分布在频谱中心位置且其宽度为物光谱的两倍,物光谱与其共轭谱分布在对称位置,物光之间的互相关项分布在物光谱之间,其宽度也是物光谱的两倍。为了避免频谱串扰噪声,频域滤波方法要求两路物光的频谱与其他7项在频谱上完全分离,这需要特殊的光路设置使多路物光具有不同的光程差[49,51],在探测器采集期间避免物光之间的相互干涉以消除互相关谱,增加光路的复杂性。此外,由于零级谱占据了接近一半的全息图频谱,限制了物光谱空间带宽利用率的进一步提升。
为了进一步克服这些限制,假设一个复函数[48]:


该复函数H(r)包含了全息图平面上的复振幅分布,对它取e指数,并用H(r)=Re[H(r)]+iIm[H(r)]展开,可得:致。证明所介绍的方法可以规避物频谱与零级谱和物体的互相关谱重叠所带来的影响。图4(a)~4(i)所展示的仅为双通道复用模型,实际系统中

图4 数值计算结果。(a)数字全息复用模型,以双通道为例;(b)~(c)2路原始物光相位分布;(d)2通道复用全息图的傅立叶频谱,物光谱与其他项完全分离;(e)~(f)对应(d)的2路重建物光相位分布;(g)2通道复用全息图的傅立叶频谱,物光谱与其他项重叠;(h)~(i)对应(g)2路重建物光相位分布;(j)8通道复用全息图的傅立叶频谱, 4路为物光1,其他4路为物光2,物光谱与其他项重叠;(k)~(l)对应(j)的其中2路重建物光相位分布Fig. 4 Numerical calculation results. (a) Digital holographic multiplexing model, taking two channels as an example; (b)~(c) phase distribution of original object; (d) fourier spectrum of the 2-channel multiplexed hologram, and the spectra are completely separated from other terms; (e)~(f) the reconstructed phases from (d); (g) fourier spectrum of the 2-channel multiplexed hologram, the object spectra are overlapped with other terms; (h)~(i) the reconstructed phases from (g); (j) fourier spectrum of 8-channel multiplexed hologram, 4 channels are the object 1, the other 4 channels are the object 2, and the object spectra are overlapped with other terms;(k)~(l) two of the reconstructed phases from (j)
其中,Re和Im分别表示取实部和虚部。从式(4)可知,复函数H(r)的实部包含了全息图的强度函数和参考光的强度函数,其虚部可以采用希尔伯特变换得到:

其中,p.v.表 示取柯西主值,τ为中间变量。此时,可完全获得复函数H(r)的实部和虚部,利用式(3)可以直接重构物光的复振幅分布,无需使多路物光与其自相关谱或互相关谱完全分离。该方法可以进一步简化复用光路成本,仅需满足希尔伯特变换的适用条件[48,52-53],即H(r)满足解析性要求。将式(3)用泰勒展开式表达:
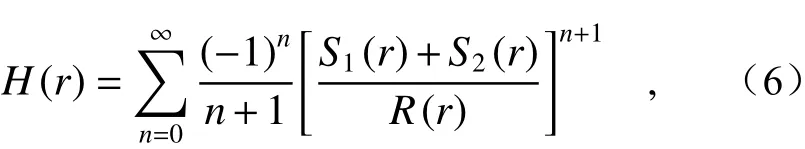
其中,参考光的强度需大于物光的强度以实现泰勒展开,同时从式(2)可见,较高的参考光强度可以提升物光项在频域中的衬度。此时H(r)的解析性等价于 [S1(r)+S2(r)]/R(r)的解析性,即物光为频域单边带信号,分布于频域半轴上。
4.2 数值计算结果
图4(彩图见期刊电子版)展示了所介绍方法求解的数值计算结果,图4(a)为两通道全息复用模型,物光1、物光2与参考光成一定夹角,探测器记录其干涉条纹。图4(b)~4(c)为物光1与物光2的相位分布图。此处展示的为光路复用的通用模型,假设两路物光在探测器中是独立的。图4(d)与4(g)展示了两路复用全息图的傅立叶频谱,对应物光谱与其他谱非重叠和重叠情况。图4(e)~4(f)与图4(h)~4(i)展示了相应的重建结果。可见,无论物光项是否与其他项重叠,重建的归一化均方误差(Mean Square Error, MSE)均一引入更多物光可实现更丰富的应用。在视场拓展应用中,可引入更多物光形成干涉图,比如2014年所报道的3倍视场拓展的全息复用系统[54]实现了超越相机视场3倍的离轴全息成像。同时在分辨率拓展应用中,每一路物光携带了物体不同方向的高频信息,最终将对应的高频成分拼接形成完整的物体频谱,为了尽可能获得近似各向同性的频率分量。至少需要3组不同方向的频率成分[18,20]。如图3(c)所示的分辨率提升方法,则采用了6路通道的全息复用方法,从单帧全息图中获得了6组不同方向的空间频率成分[49]。多通道复用的实质是多物光从不同方向入射至相机,与参考光干涉形成强度图,因此各物光在干涉图频域中的分布位置不同,这为物光分离重建提供了基础。进一步,图4(j)展示了8路复用全息图的傅立叶频谱。在计算中,其中4路物光设置为物光1的分布,另外4路物光设置为物光2的分布,8路物光传输方向相互具有一定的夹角。图4(k)~4(l)展示了物光谱1与物光谱2的重建结果。此时重构的MSE均与图4(e)~4(f)中的相同,也就证明了所介绍方法可不受限于物光谱的特定排布,无论物光谱是否与零级项或者互相关项重叠,均可提取原始的物光频谱并准确重构。数值计算结果表明,该高通量数字全息复用求解方法可以进一步容纳更多的物光信息,超越传统复用框架下的空间带宽利用率极限,最高可达78.54%[48]。该结果基于Matlab数值软件计算得到。
多光束复用模型将引入多束光干涉,并且参考光的强度需要大于物光光强,这对采集相机的动态范围提出了要求。图5(a)(彩图见期刊电子版)展示了在参考光振幅值为物光2倍的情况下,重建MSE随相机位深变化的结果。数值计算中的参数与图4相同。可见,在双光路复用的情况下,当相机位深在5比特以上时,重建MSE均降低到10-4量级。图5(b)(彩图见期刊电子版)展示了相机位深为8比特情况下,重建MSE随参考光光强变化的情况。此时两路物光的最大振幅设置为1。可见,当参考光振幅大于1时,重建MSE随光强变化趋势变缓。实际应用场景中,通常采用位深为8比特以上的相机,并且使参考光的振幅值大于物光的2倍,可实现较好的结果。

图5 数值计算结果。(a)相位重建MSE随采集位深变化的结果;(b)相位重建MSE随参考光振幅值变化的结果Fig. 5 Numerical calculation results. (a) The MSE result of phase reconstruction as a function of acquisition bit depth; (b) the MSE result of phase reconstruction as a function of the amplitude value of reference wave
4.3 高通量数字全息显微系统
本文介绍的面向高通量的多路复用数字全息求解方法对应的高通量数字全息显微镜示意图如图6(a)(彩图见期刊电子版)所示[48]。输出波长为632.8 nm的激光器经过扩束准直后由分束器BS1分成照明光和参考光。照明光照射样本后形成物光,经过显微物镜(20×,0.42NA)和筒镜(L3)组成的透射式明场显微成像系统。分束器BS2、反射镜M2和反射镜M3组成视场复用系统,其结构如图6(b)(彩图见期刊电子版)所示,复用系统放大率为1。透射式明场显微系统出射的物光被分束器BS2分成两部分,并分别被反射镜M2和反射镜M3反射,形成两路物光S1(r) 和S2(r)。反射镜M2和反射镜M3可旋转以调节两路物光的出射方向。其映射在相机的视场范围内,如图6(c)(彩图见期刊电子版)所示,两物光路映射在相机平面中光学信息对应于物体的不同区域,这就实现了拓展视场的复用效果。合束器BS3将两路物光和参考光相结合,经过偏振片P映射到探测器中,实现双光路复用系统。两路物光的入射方向不同,与参考光在相机平面干涉形成强度图,因此各物光在频域中分布的位置不同,提供了物光分离重建的基础。在本系统中,探测器像素尺寸为5.86 μm。

图6 高空间带宽利用率数字全息显微镜光路示意图。(a)视场拓展数字全息显微系统;(b)光路复用示意图;(c)视场复用示意图[48]Fig. 6 Schematic diagram of the optical path of a digital holographic microscope with high spatial bandwidth utilization. (a) Extended field-of-view digital holographic microscope; (b) schematic diagram of optical multiplexing setup; (c) schematic diagram of field-of-view multiplexing[48]
本文所设计的高通量数字全息显微镜,实验成像结果如图7(彩图见期刊电子版)所示,物体为定量相位型标靶图案(Quantitative Phase Microscopy Target, QPMT, Benchmark Technologies Corporation, USA)。图7(a)为所设计的高通量数字全息显微镜采集的复用全息图,图7(b)为其傅立叶频谱。物光谱范围由系统的相干传递函数决定,其半径为 (NA)/(Mλ),其中NA为系统的数值孔径,λ为照明波长,M为成像放大率。可见,在该系统中,物光谱1与物光谱2的范围较大,在全息图频谱上不可避免地与零级谱相互重叠,占据了全息图频谱的右半侧。图7(c)为其定量相位重建结果,其中红色区域为相机的采集视场范围,其重建区域超出相机视场范围1.94倍,并在实验上实现了66.8%空间带宽利用率的定量相位成像,超越了当前单帧离轴复用全息图的带宽利用率极限58.9%[45,48]。图7(d)和7(e)分别为传统离轴全息显微镜所采集到的全息图及其频谱,显微物镜(20×,0.42NA)和筒镜(L3)的参数不变,后端加入4f系统且其放大率调整为2,并取消其中1路的反射形成单物光光路,物光的相干传递函数半径将减半,此时的±1级可与零级完全分离,形成常规的离轴全息频谱。其定量相位重建结果如图7(f)所示。图7中两系统所采用的显微物镜参数是完全相同的,意味着系统的衍射极限分辨率相同,并且都可从单张全息图中复原物光波,仅总的放大倍率不同。可见所设计的高通量数字全息显微镜在不改变光学衍射系统参数和探测器参数的情况下,最终成像视场以及空间带宽积较传统离轴全息显微镜提高了8倍,实现了单帧高通量数字全息显微成像。该系统以视场复用方法展示了高通量数字全息复用技术的实际应用,与传统离轴复用数字全息框架下的系统原理类似[47,54]。相比于文献[54]所报道的超越相机视场3倍的离轴全息成像结果,虽然本实验系统仅实现2倍的相机视场拓展,但本系统中物光谱所占全息图频谱的面积比值更大,因此全息图空间带宽利用率更高,重构的空间带宽积将提升。在相同衍射极限的情况下,该系统所展现的成像视场更大。单通道离轴全息也可通过多个4f系统引入柱透镜,使物函数沿干涉条纹方向拉伸实现高空间带宽积成像[53],这对光源的相干性提出了较高的要求。而基于多通道全息复用方法可以补偿光源相干性所产生的影响[47],提升定量相位成像的环境适应性,结合所介绍的高通量数字全息复用求解框架,可进一步推动无标记显微成像步入高通量应用。

图7 高空间带宽利用率数字全息显微镜重建图像[48]。(a)高通量复用全息图;(b)复用全息图的频谱;(c)高通量定量相位重建结果;(d)传统数字全息显微镜得到的全息图;(e)传统离轴全息频谱;(f)传统离轴全息重建结果Fig. 7 Reconstruction images from digital holographic microscope with high spatial bandwidth utilization[48].(a) Multiplexed hologram; (b) spectrum of the multiplexed hologram; (c) high-throughput quantitative phase reconstruction from (a); (d) the hologram image obtained by conventional off-axis digital holographic microscope; (e) spectrum of conventional off-axis hologram; (f) the reconstruction results of conventional off-axis hologram in (d)
5 结 论
随着计算机和探测器的性能发展,计算方法改变了传统“所见即所得”的成像模式,通过对光学照明和成像系统进行光学编码,配合与之相适应的数字解码过程,可使重构场景逐渐接近理想结果。本文分析并总结了实现高通量成像的有效方法,一种思路是通过采集海量数据利用数据冗余和计算算法重构具有高空间带宽积的图像,可实现空间域拓展和频域拓展,但需要采集多幅含有物体不同信息的图像,不可避免地牺牲了时间自由度。提升采集数据的利用效率也是实现高通量成像的有效途径,可以降低对源数据冗余量的要求。本文介绍的高通量数字全息复用技术可充分利用单幅强度图像冗余的空间带宽,可提升源数据的利用效率,即从单帧强度图复原更多物体的信息,基于该技术所设计的高空间带宽利用率数字全息显微镜在不改变光学衍射系统参数和探测器参数的情况下,最终成像视场以及空间带宽积较传统离轴全息显微镜提高了8倍。该技术可直接实现拓展成像视场、拓展成像分辨率、拓展成像深度等性能,可进一步拓展至波长复用、角度复用、时分复用和多模态荧光复用等。该方法结合数字全息所特有的定量性优势,能够有效提高现代光学显微镜的成像性能,在高通量、大规模无标记生物样本研究和分析中有广阔的应用前景。

