可变速抽水蓄能发电电动机多目标优化设计

胡金明，孙玉田，张春莉，李桂芬，胡 刚

(水力发电设备国家重点实验室(哈尔滨大电机研究所)，哈尔滨 150040)

0 引言

抽水蓄能电站具有调峰、调频、负荷跟踪及事故备用、消纳新能源等功能，对提升电网质量和能源综合利用水平具有重要作用。我国抽水蓄能电站采用的是定速抽水蓄能机组。与定速抽水蓄能机组相比，变速抽水蓄能机组可以提高水泵水轮机运行效率，提高机组运行稳定性，还具有独立的有功、无功控制，提高机组快速响应能力等一系列优势。因此，变速抽水蓄能机组越来越引起重视，逐渐被业界推崇。

目前，国内可变速抽水蓄能机组仍未进行工程建设，科研成果多为控制系统研究。其电机设计以及电磁性能研究较少，多为理论研究，暂无优化方面成果。电机优化方面论文也多为笼型感应电机和永磁同步电机的性能优化设计。笼型电机优化目标多为效率、成本、功率因数、最大起动转矩和起动电流等。永磁同步电机优化目标多为齿槽转矩、最大转矩、转矩脉动等。文献[1]引入改进的粒子群优化算法对永磁同步电机进行多目标优化，降低损耗，提高效率。文献[2]提出了一种采用克里金代理模型算法的多目标优化方法对永磁电机进行优化设计。文献[3]采用拟牛顿方法和模式搜索方法对一台汽车用永磁发电机进行了优化设计。文献[4]提出了采用曲面响应法优化辅助槽尺寸的方法。文献[5]采用正交试验表获得样本空间，通过响应面法建立优化目标及约束条件的优化模型，最后利用粒子群算法对优化模型进行求解。文献[6]提出基于遗传-模式搜索算法的异步电机多目标优化设计方案。

对于可变速发电电动机，其由背靠背变流器进行供电和调节，可实现软起动，故最大起动转矩和起动电流不是主要影响因数，且其无齿槽转矩问题，故本文以此电机的效率、成本为优化目标，以转子电流密度为约束进行优化设计。

1 优化变量及优化目标的确定

本文以一台10 MW可变速发电电动机为研究对象，根据发电电动机的设计要求和电机设计原则提出基本结构和绕组形式等，并建立参数化有限元分析模型，通过场路耦合有限元仿真分析，得到初步电磁设计方案。电磁参数如表1所示，定转子槽形均选择开口槽。

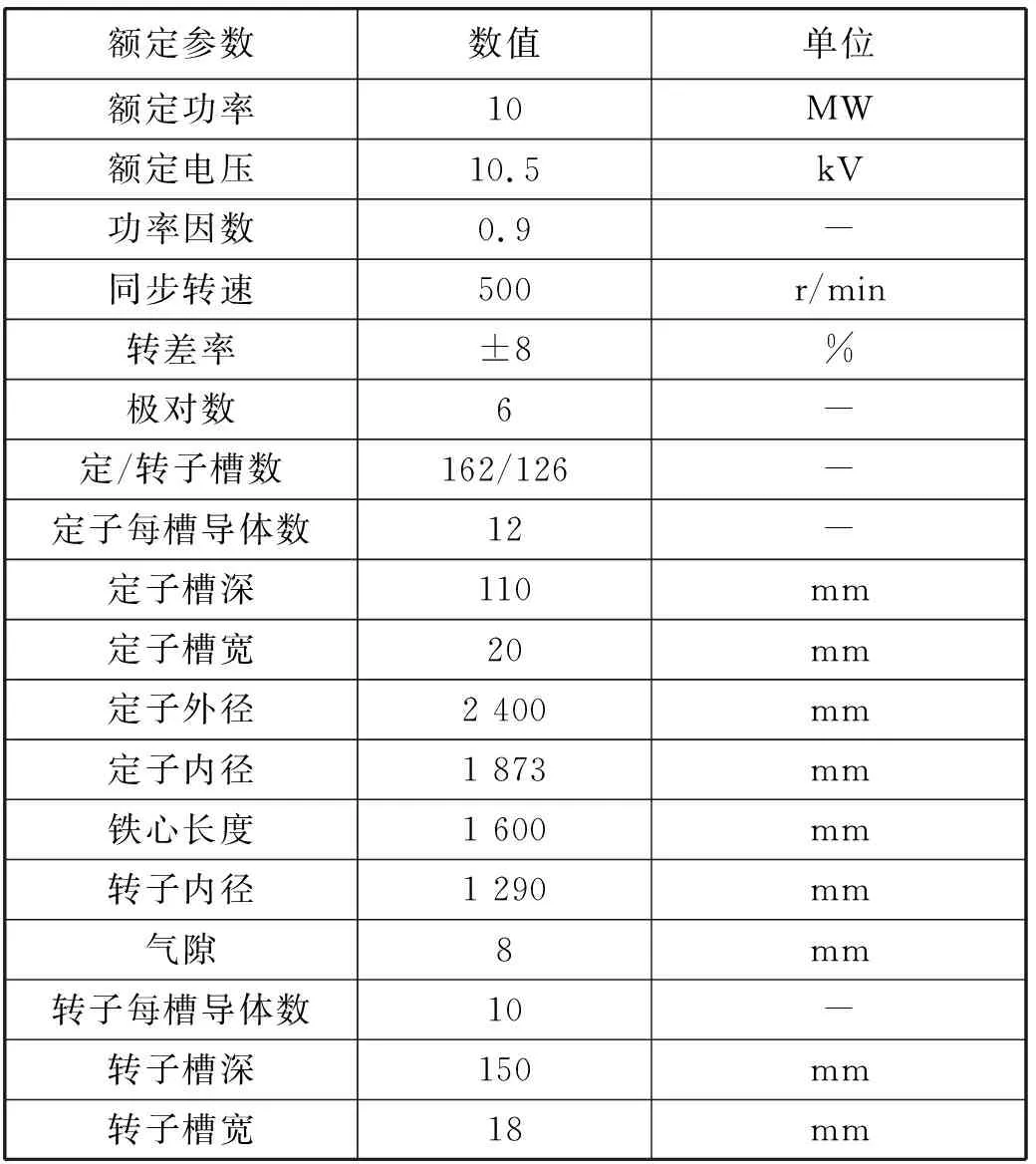
表1 可变速电机主要参数

本文采用时变电磁场有限元法进行仿真计算。首先，建立有限元求解场域，由于10 MW可变速发电电动机定子绕组每极每相槽数为4.5，为分数槽，因此有限元计算中需采用偶对称边界条件，故本文建立了一对极的求解场域，如图1所示。定义10 MW可变速发电电动机内外表面弧ab和gh为一类齐次边界条件，定义ac、bd、eg、fh为整周期边界条件。其瞬态磁场用矢量磁位描述，方程为：

(1)

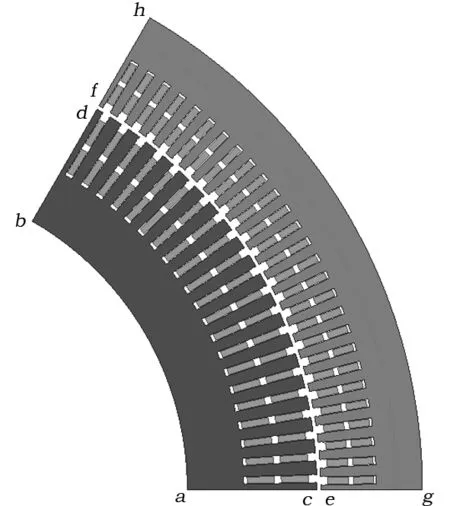
图1 求解场域

根据可变速发电电动机的实际情况，选取电机效率、成本作为优化目标，转子电流密度为约束目标。

电机的效率指输入功率和输出功率的关系，也是电功率和机械功率的转换关系，求解方程如下所示：

(2)

式中：Po为输出功率；∑Pt为电机的损耗之和，主要包括铁心损耗、绕组损耗、机械损耗、风摩损耗和杂散损耗等。

损耗中铁心损耗和绕组损耗占主要成分，绕组损耗的计算如下式所示：

PCu=3RsI2

(3)

式中：Rs为相电阻。

铁心损耗的计算一般采用Steinmetz方法，将铁耗分为磁滞损耗和涡流损耗两个部分，如下式所示：

(4)

式中：Ph为磁滞损耗；Pe为涡流损耗；kh为磁滞损耗系数；γ一般取值在1.8～2.2之间；ke为涡流损耗系数。

电机的主要成本包括定、转子铁心和绕组成本，通过对电机的铁心和绕组成本共同优化可以达到合理分配铁心设计和绕组设计。其公式如下式所示：

C=MFeCFe+MCuCCu

(5)

式中：MFe为定、转子铁心总重量；CFe为铁心的单价；MCu为定、转子绕组总重量；CCu为绕组的单价。

可变速发电电动机的转子绕组多采用单支路设计，便于端部连接等，其电流密度较高，直接影响转子的热负荷，且由于转子的散热条件相较于定子较差，故需要将其作为约束，避免在优化过程中转子电流密度过高，导致电机设计温升较高。

本文选择定子外径、定子内径、转子内径、铁心长度、定子每槽导体数、转子每槽导体数、定子槽深、定子槽宽、转子槽深、转子槽宽、气隙长度为优化变量，优化变量的取值范围如表2所示。

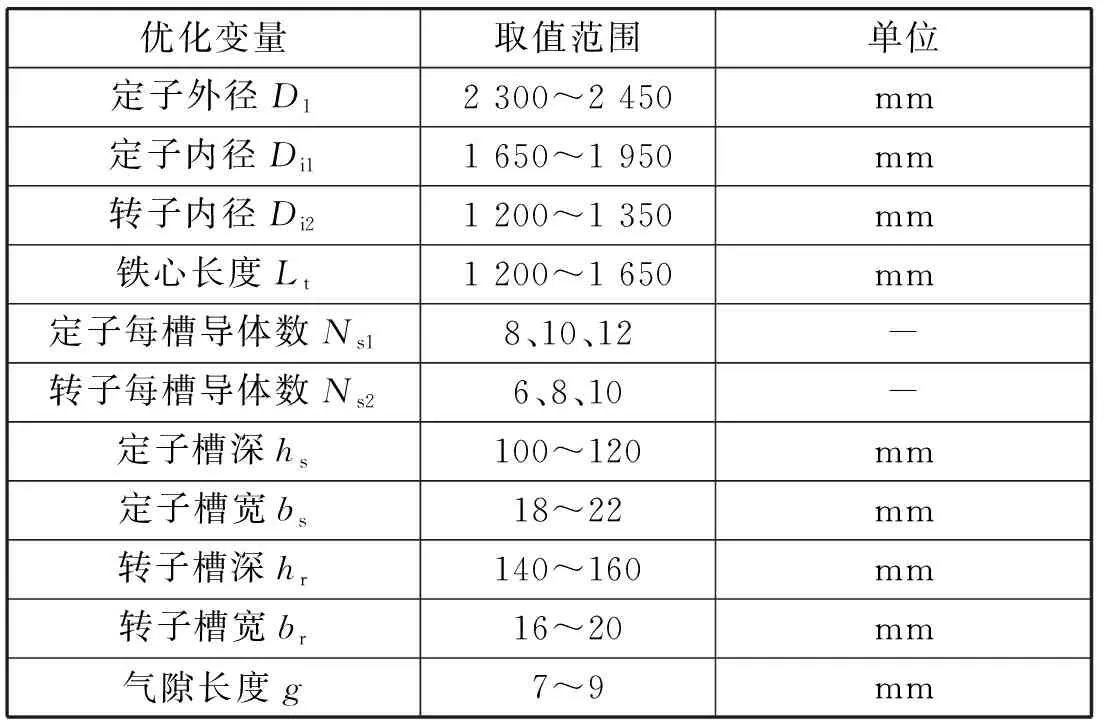
表2 优化变量取值范围

2 试验设计

本文采用拉丁超立方抽样方法进行试验设计，从多元参数分布中近似随机抽样，属于分层抽样技术，分层采样的样本值能够覆盖输入随机变量的整个分布区间，达到样本重复少的目标，可以在有限的试验次数中获取到较多有效的试验结构。对所选取的11个优化变量进行试验设计，输入参数与输出参数的线性相关性结果如表3所示。其中与效率和成本目标相关系数较大的量为主影响参数(若仅与转子电密相关系数较大将不作为主影响参数)，包括定子外径D1、定子内径Di1、转子内径Di2、铁心长度Lt、定子每槽导体数Ns1、转子每槽导体数Ns2六个参数。

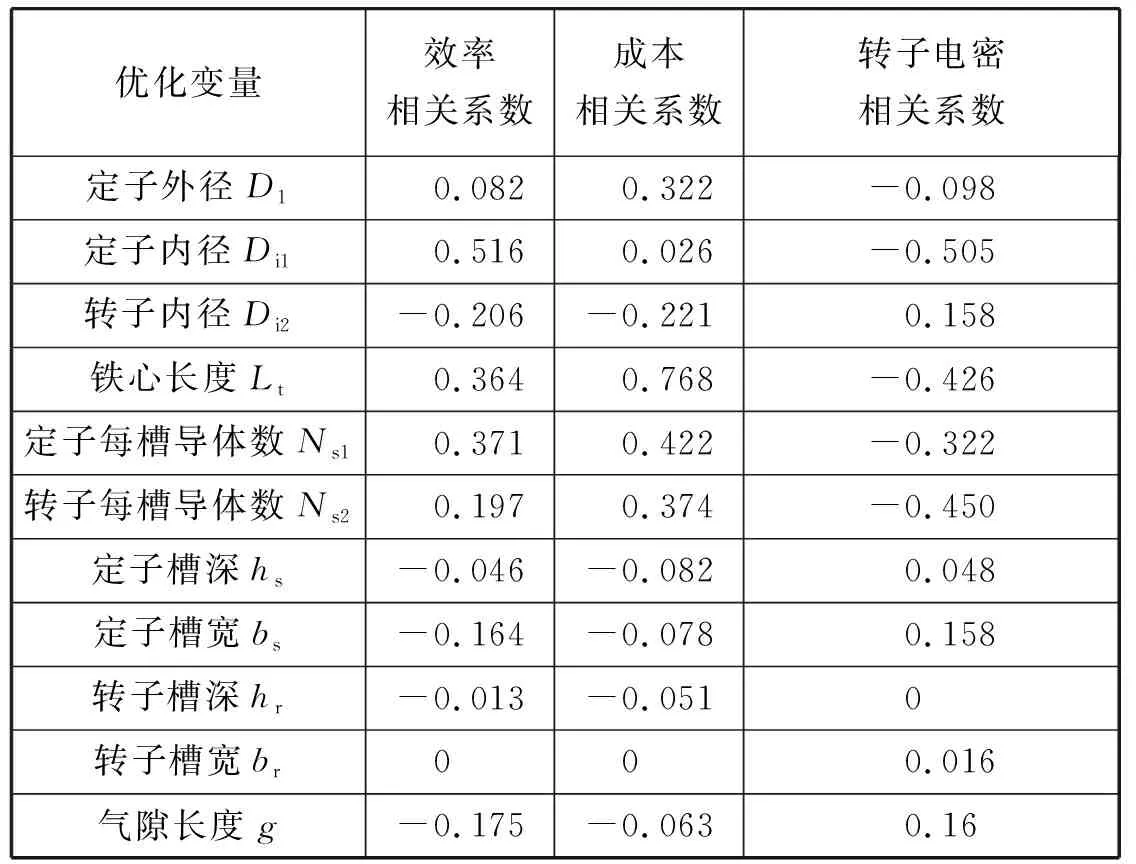
表3 输入参数与输出参数的线性相关性

3 响应面法优化

本文采用克里金法进行响应面拟合。克里金法是依据协方差函数对随机过程进行空间建模和预测的回归算法。在特定的随机过程，例如固有平稳过程中，克里金法能够给出最优线性无偏差估计，因此在统计学中也被称为空间最优无偏差估计器。对于电机的参数优化，具有很强的非线性，无法用一次函数和二次函数去拟合，所以克里金法具有较大的优势。

分别进行11个全参数和6个主参数进行试验设计，克里金法抽样数分别设定为100、200和400。利用预测系数来评价响应面拟合的准确性，预测系数越接近100%表明映射关系就越好，仿真结果如表4所示。

从表中可以看出，相关度不高的参数将严重影响拟合优度，且抽样点数对拟合优度的影响非常大。其中拟合程度最佳的是6个主参数，400个抽样点的方案，其成本预测系数值为99.6%，转子电流密度预测系数值为98.2%，成本预测系数值为88.6%，可以较好的获得响应面。由此建立了6个主参数，抽样400个点拟合的响应面。

响应面建立后，使用遗传算法基于响应面进行优化。由于响应面是一个拟合的多元线性方程，所以基于多元线性方程优化可大大减小仿真时间，快速找到优化方案。但是这种优化方法受到预测系数的影响，得到的方案是预测值，并非仿真值，需要对优化参数重新进行仿真验证。通过遗传算法优化获得帕累托前沿线，如图2所示。帕累托前沿线上的点均是优化过程中的最优点，但是通常目标变量的选取是互相冲突的，一个目标有所改善往往伴随着另一个目标的变差，所以可以通过试验数据点获取一条最优前沿线，再根据实际工程需要选取最优方案点。图2中帕累托前沿，#1397点为本次选取的最优点，对应优化设计方案如表5所示。

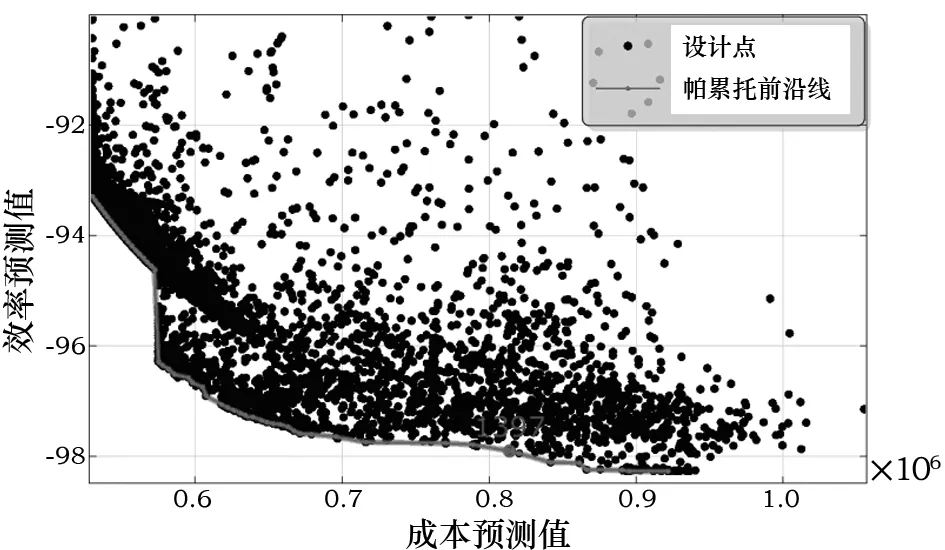
图2 优化帕累托前沿图

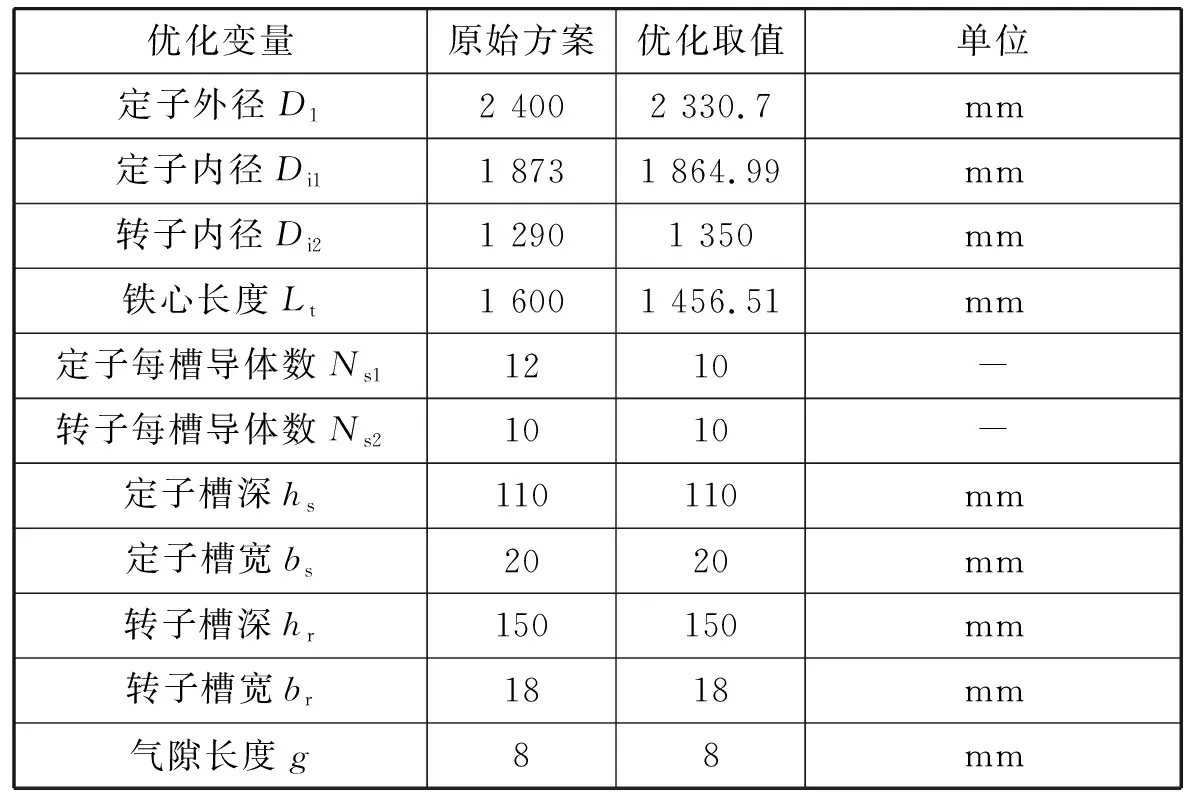
表5 响应面法优化方案

对优化方案进行有限元仿真，获得目标变量的预测值和仿真值、约束变量的预测和仿真值如表6所示。预测值与仿真值误差较低，证明响应面法优化的准确性。

表6 响应面法优化方案仿真结果

4 直接优化法优化

直接优化法采用遗传算法分别对11个全参数和6个主参数进行优化，帕累托前沿线图分别如图3和图4所示。优化结果如表7所示。

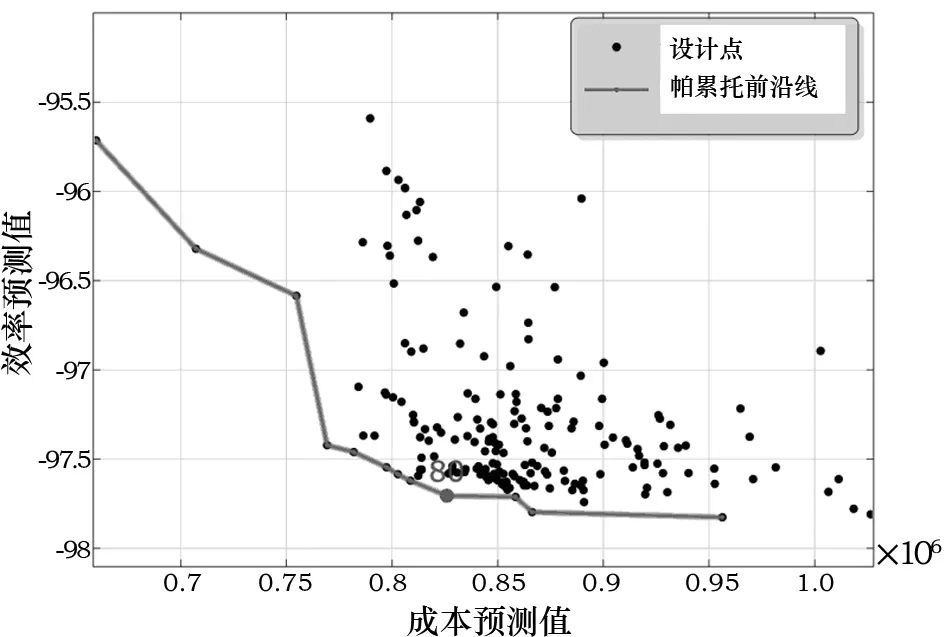
图3 11个全参数优化帕累托前沿线图

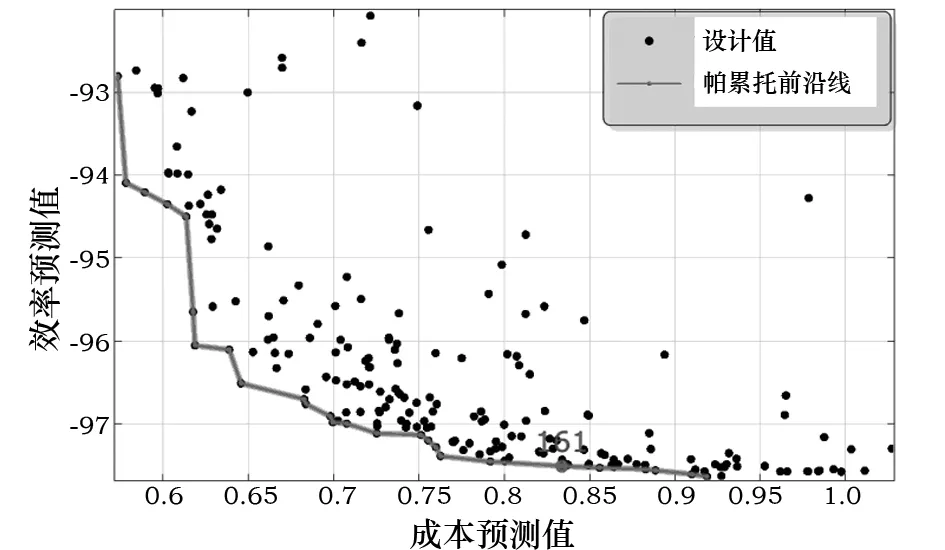
图4 6个主参数优化帕累托前沿线图

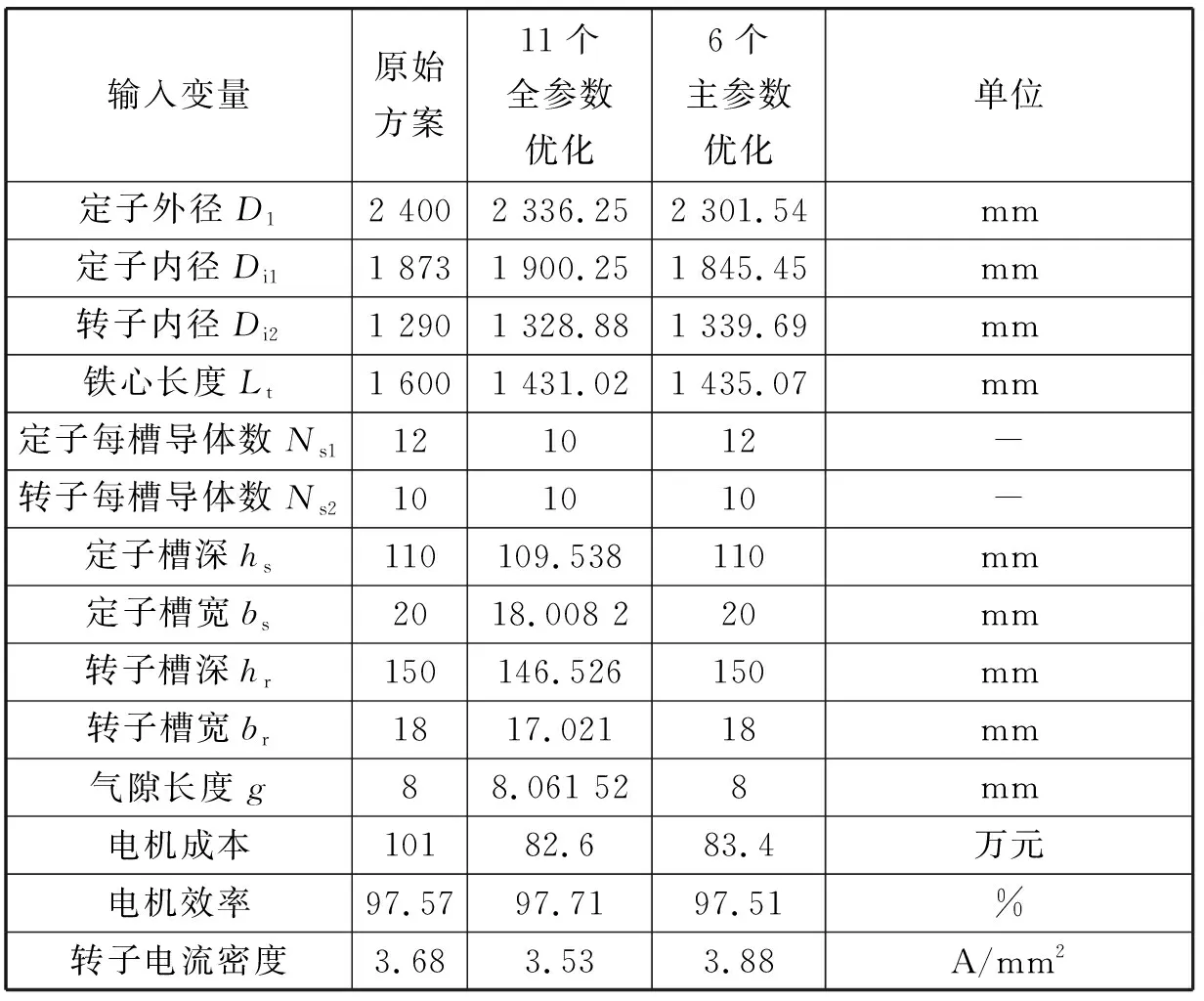
表7 直接优化法优化结果

对比表5和表7中三个优化方案，目标变量优于原始方案，且11个参数直接优化所获得的结果最优，电机成本由101万元降低为82.6万元，电机效率由97.57%提升为97.71%。

5 优化前后对比和基本电磁性能验证

响应面法对于较多优化参数或优化参数对目标参数敏感的优化项目会优于直接优化方法。直接优化方法较简单且优化效果好，但需要进行大量的有限元仿真计算，不适用于三维计算等大量消耗计算资源的项目。

选取表7中11个参数优化的结果，建立单元电机结构如图5所示。空载磁密和励磁电流对比如表8所示，从表中可以看出优化方案定转子铁心材料的利用率更高。空载磁力线分布图和空载磁密分布云图如图6和图7所示。

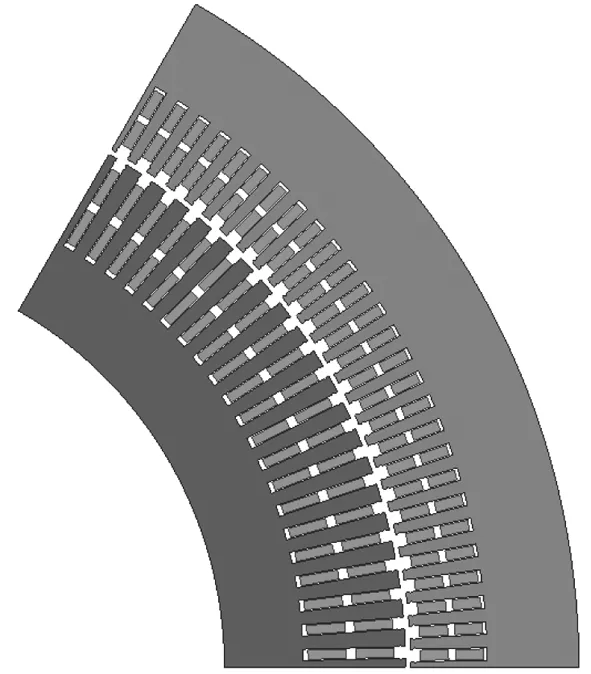
图5 优化后单元电机有限元模型

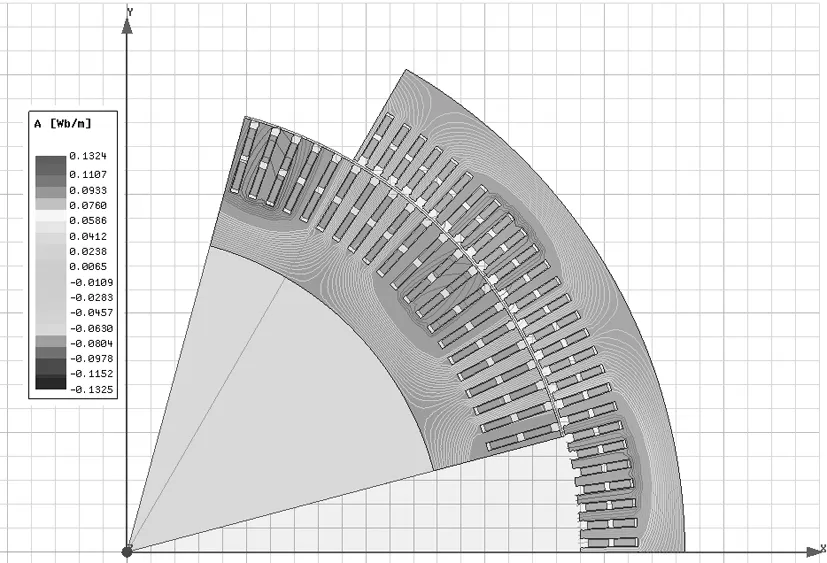
图6 优化后空载磁力线分布图

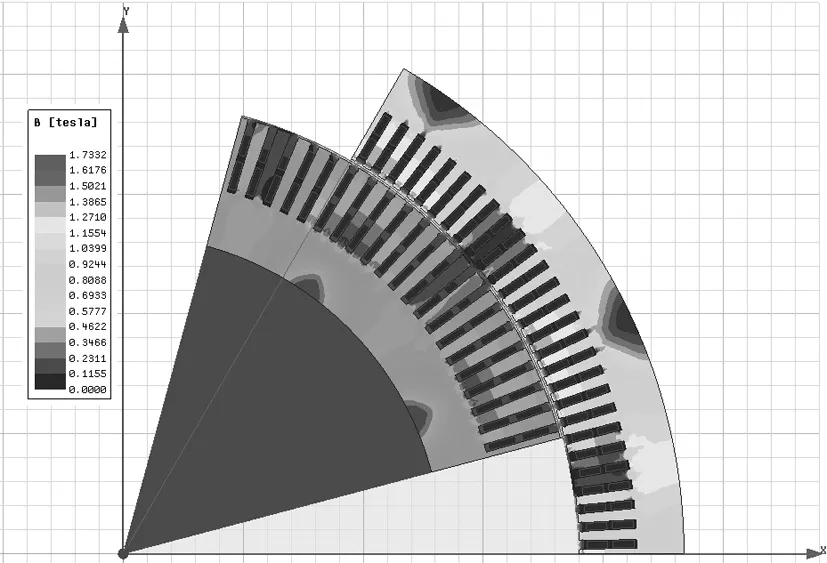
图7 优化后空载磁密分布云图

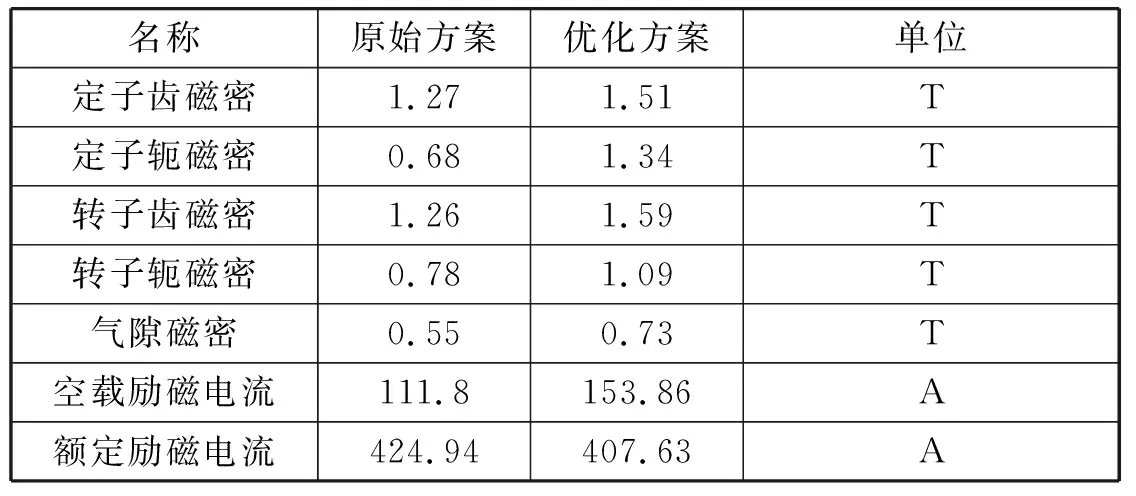
表8 空载磁密对比

6 结论

本文选取了在电机设计阶段对电机性能有影响的11个参数作为优化变量，选取电机的成本和效率两个外特性作为目标变量，选取转子电流密度作为约束变量。首先进行了相关性分析，选出对目标变量起主要作用的6个参数，然后分别进行了11个全参数和6个主参量的试验设计和响应面分析，最后进行了基于响应面的优化设计和直接优化设计，对比仿真结果。从仿真结果来看，基于响应面的优化设计和直接优化设计方法均能获得不错的优化方案，但各自有优缺点。响应面法对于更多优化参数或优化参数对目标参数敏感的优化情况会优于直接优化方法。直接优化方法较简单且优化效果好，但需要进行大量的有限元仿真计算。11个参数直接优化所获得的结果最优，电机成本由101万元降低为82.6万元，电机效率由97.57%提升为97.71%，且优化方案定转子铁心材料的利用率更高。本文为可变速发电电动机的多目标优化提供指导，实现了此台10 MW可变速发电电动机的成本、效率多目标优化，优化过程中确保了转子电密在合理范围内，以保证电机温升，对于可变速发电电动机的电磁方案设计优化乃至于其他机型电机的优化设计具有一定的参考价值。