UWB/MIMU自适应动量GD-PF室内协同定位

李 鹏，凌智琛，荣冬成，向宇翔

UWB/MIMU自适应动量GD-PF室内协同定位

李 鹏，凌智琛，荣冬成，向宇翔

（湘潭大学自动化与电子信息学院，湖南湘潭 411100）

针对超宽带（UWB）室内定位时容易受到非视距误差影响，导致定位精度大大下降，甚至无法准确定位的问题，提出了一种UWB/MIMU自适应动量梯度下降-粒子滤波（GD-PF）室内协同定位方法。首先在梯度下降算法中引入指数加权平均和变步长策略，加快解算速度；然后采用粒子滤波对UWB解算数据进行优化，减小粗差对定位精度的影响；最后引入自适应函数调整扩展卡尔曼滤波（EKF）增益，对UWB和微型惯性测量单元（MIMU)的定位数据进行联合滤波。UWB/MIMU协同定位实验结果表明，自适应动量GD-PF协同定位算法与传统定位算法相比，能有效消除非视距误差的干扰，提高室内定位精度和鲁棒性。

超宽带；微型惯性测量单元；梯度下降算法；粒子滤波；自适应扩展卡尔曼滤波

0 引言

随着信息时代的飞速发展，对于位置服务精度的要求越来越高。在室外，有全球卫星导航系统（global navigation satellite system, GNSS）能够带来很好的定位精度，但在室内因有建筑物等遮挡物的影响，定位精度较差。据统计，80%的定位服务需求发生在室内[1]，因此建立一个高精度、连续的室内定位系统是非常有必要的。目前，室内环境的无线定位技术得到了广泛的研究，包括伪卫星技术、蓝牙、紫蜂（zigbee, ZB）、超宽带（ultra wide band, UWB）等[2-3]。超宽带技术作为近年来室内定位中非常热门的一种定位方式，由于具有时间分析率高、穿透性强、覆盖范围广、系统复杂度低、抗多径效应良好等优势，越来越受到广大公司和研究者的重视[4-5]。

传统的定位算法如最小二乘法、文献[6]提出的算法等，只有当系统的测量误差处于理想高斯分布时，才能达到较高的精度。然而室内环境复杂多变，常常会处于非视距环境[7]（non line of sight, NLOS）。为了进一步提高室内定位的可靠性和准确性，多传感器融合定位技术引起了国内外学者的关注，比如把射频识别[8]或者微型惯性测量单元（miniature inertial measurement unit, MIMU）与UWB融合。扩展卡尔曼滤波（extended Kalman filter, EKF）在多传感器融合定位系统中得到广泛应用。

为了减少非视距环境的影响，提高室内定位的精度，本文提出了一种UWB/MIMU自适应动量梯度下降-粒子滤波（gradient descent-particle filter, GD-PF）室内协同定位方法。UWB的定位信息，首先通过改进的动量梯度下降算法解算，然后采用粒子滤波对估计位置进行再次优化，最后使用自适应EKF将其与MIMU的数据融合，得到准确的定位结果。

1 UWB定位方法

室内定位中，对位置进行解算，首先要从信号模块上得到各个基站与标签之间的距离，再使用距离信息代入定位算法进行计算。测距过程中，可以通过时间、角度和信号强度3种方法来得到距离信息。

本文中UWB的测距方法是信号到达时间[9]（time of arrival, TOA），测量定位过程中标签和基站之间信号传播的时间，根据UWB的传播速度，将时间转换成距离信息。TOA进行定位至少需要3个基站。3个基站可进行二维定位，理想状态下的TOA定位原理如图1所示。

以基站位置为圆心，基站与标签的距离为半径画圆，其交点为标签的位置。图中基站的数量和位置都是已知，令标签坐标位置为（，），通过TOA算法得到标签到基站的时间分别为1、2、3，根据几何原理和已知的数据，可得到的方程组为

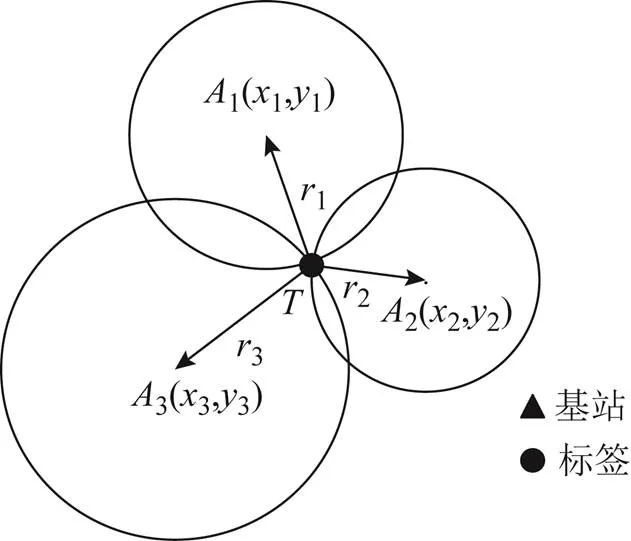
图1 TOA定位原理

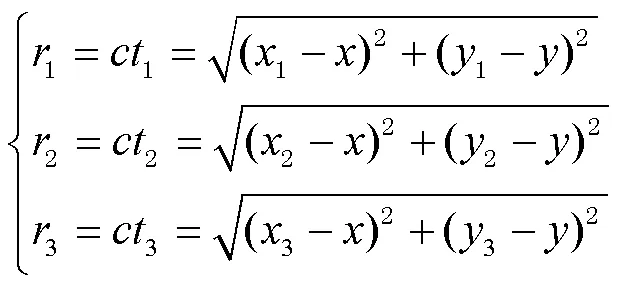
式中为UWB信号传播速度。按照方程组即可求出定位标签的二维位置。

4个及以上的基站则可进行三维定位，其方程组为

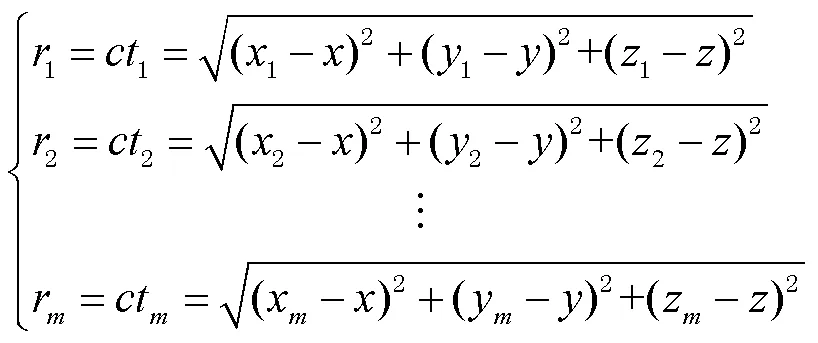
式中为基站数量。该方程组可求出标签的三维位置（，，）。

在理想状态时，可通过对式（1）、式（2）得到唯一的结果，但因为实测距离存在误差，可以通过方程组求出最优解。

2 动量GD-PF算法

2.1 动量梯度下降算法

获取UWB模块得到的距离信息，解算结果的过程，用得较多的是最小二乘算法。最小二乘算法在视距环境下该方法可以得到不错的定位结果，但在NLOS环境下精度大大降低。本文采用动量梯度下降算法对UWB得到的距离信息进行优化解算。

按照梯度下降法[10]，对于一个函数而言，从某个初始值开始，不断往梯度方向进行迭代，通过迭代，最后稳定在最优值左右。动量梯度下降法在梯度下降算法基础上对梯度进行改进，加快了位置解算速度，收敛也更加迅速。

从UWB模块中获得的距离信息，按照标签和基站之间距离，建立多元非线性模型为

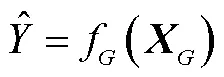
求出其均方误差为

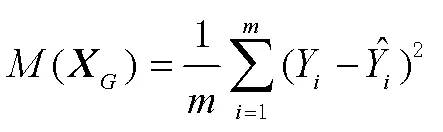
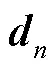
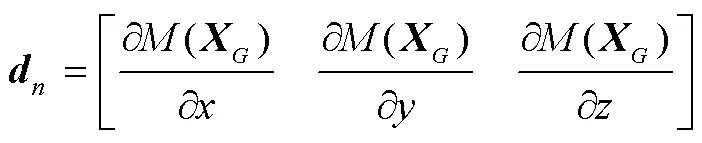
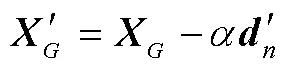
2.2 改进动量梯度下降法

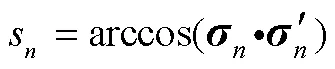
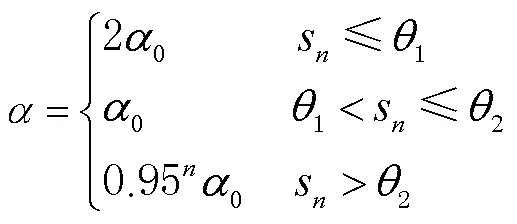
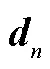
2.3 粒子滤波

粒子滤波[11]与传统的滤波算法比较，在非线性上适用，并且也适用于非线性及非高斯噪声环境的优点。所以使用其对UWB解算数据进行优化。其数学模型为：

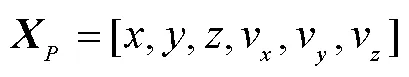
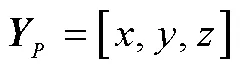
其具体步骤如下：

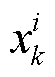
2）预测。根据状态方程，得到预测粒子为

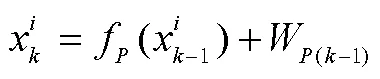
3）校正。进行权值计算，进行权值计算，越接近于观测状态的粒子，其权重越大，粒子的权值为

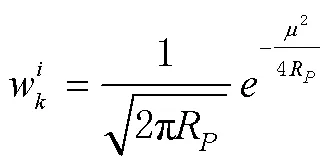
4）重采样。在重采样阶段，选择随机重采样，将[0,1]均匀分成相互独立的层，令为[0,1]均匀分布的随机变量，产生一个随机数，根据其落在的区间，所对应的随机变量就是所需要的输出量。本质是根据权重的大小进行筛选。筛选过程中，既要大量保留权值大的粒子，又要有一小部分权值小的粒子，得到新的粒子群，继续进行滤波。

进行权值归一化，为

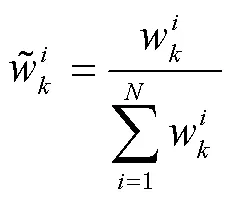
求出时刻的样本均值，即

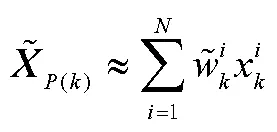
将重采样后的粒子结合速度信息通过状态方程得到新的预测粒子，即回到第2）步。

2.4 改进动量GD-PF算法

改进动量GD-PF的具体步骤：

4）依照公式得到梯度和步长，更新下一步的位置，转步骤2）。

5）使用改进动量梯度下降算法解算出该时刻的位置，再进行粒子滤波，得到该时刻使用改进动量GD-PF算法得到结果。

6）返回步骤1），继续对后续时刻的位置进行解算。

3 自适应EKF算法

3.1 UWB/MIMU融合定位方程

本文将UWB的数据和MIMU的数据结合，进行融合定位，可以补偿各自的缺点，能够更好地改善受到非视距影响的定位精度。在组合导航系统中，滤波算法对导航定位的解算精度有重要的影响[12]。

使用自适应EKF将UWB的定位数据和MIMU取得的信息进行融合，能够结合二者的优点，使定位更加准确。

UWB的定位数据是通过改进动量GD-PF算法解算的结果，根据MIMU的陀螺仪、加速度计得到的数据，从陀螺仪得到的数据是载体坐标系下、、轴方向的加速度大小情况以及俯仰角、滚转角、航偏角。首先需要将MIMU的信息从载体坐标系转换成导航坐标系下的加速度矢量。将得到的加速度矢量和UWB得到的定位坐标为该系统的观测值，该系统的方程组为

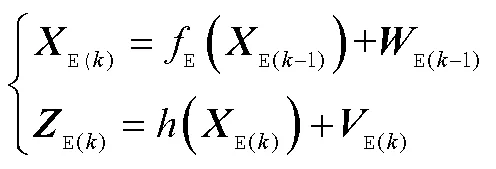
3.2 扩展卡尔曼滤波

扩展卡尔曼滤波建立在卡尔曼滤波的基础上，其核心思想是，对非线性系统，通过对状态方程和观测方程展开Taylor级数并忽略二阶及以上项，得到近似的线性化模型，最后在应用Kalman滤波完成对目标估计等处理[13-14]。

扩展Kalman滤波的公式如下：

1）通过上一时刻的定位信息和状态方程得到该时刻下的状态值，以及通过UWB和MIMU在当前时刻得到的信息来取得观测值。

2）将状态方程和观测方程进行微分和对协方差进行预测，即：

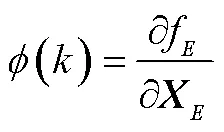
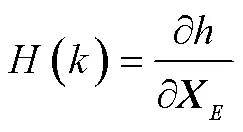
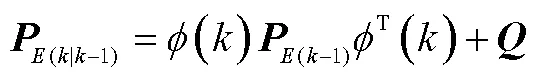
3）更新估计值和协方差为：

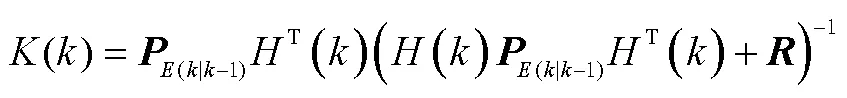
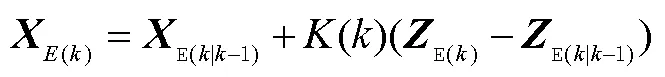
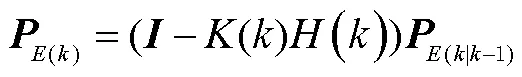
以上为一个计算周期，各个时刻对其进行EKF处理，就是在这个计算周期内进行循环。

3.3 自适应EKF

本文中自适应的作用是修正当目标状态受到环境影响，有可能产生异常观测值情况下的定位结果，从而减少异常值的影响，提高定位精度。

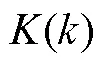
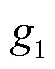
状态误差和观测误差是有限的，同一时刻UWB/MIMU得到的状态值和观测值之间的距离若过大，说明该时刻受到了异常值的影响，从而使得误差较大。

同样，因为在室内定位的过程中，目标的速度是有上限的。在连续2个时刻的UWB位置的距离若过大，UWB的定位就会在当前时刻受到非视距的影响。

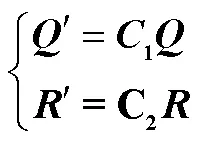
4 自适应动量GD-PF协同定位算法

本文使用了自适应动量GD-PF协同定位算法。首先通过TOA方法从UWB模块上得到距离信息，使用动量GD-PF算法处理其距离信息，得到UWB的定位结果；然后通过自适应EKF算法来融合MIMU模块中加速度计和陀螺仪的数据；最终得到融合定位结果。其算法结构如图2所示。

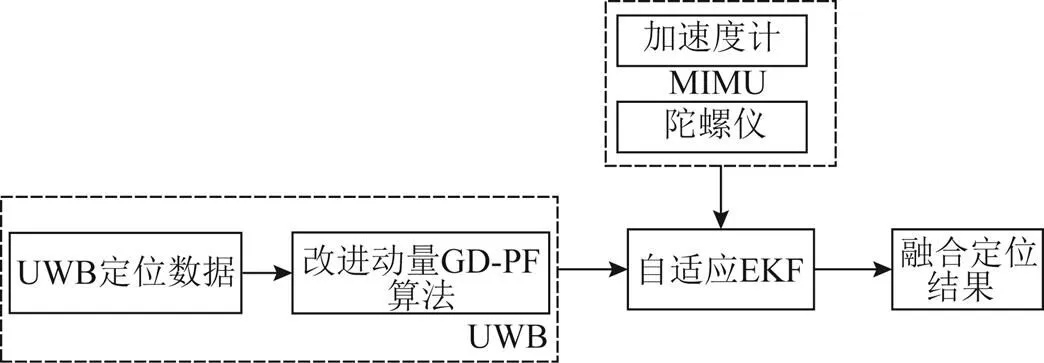
图2 自适应动量GD-PF算法

5 实验与结果分析

5.1 实验环境

为了对自适应动量GD-PF算法进行性能评估，通过UWB/MIMU室内融合定位系统来验证。该系统中有4个基站1、2、3、4，通过障碍物来制造NLOS环境。

在实验环境中，进行了多种路径的实验，从中选择2种路径来进行数据分析，其实际路径和基站分布如图3所示。

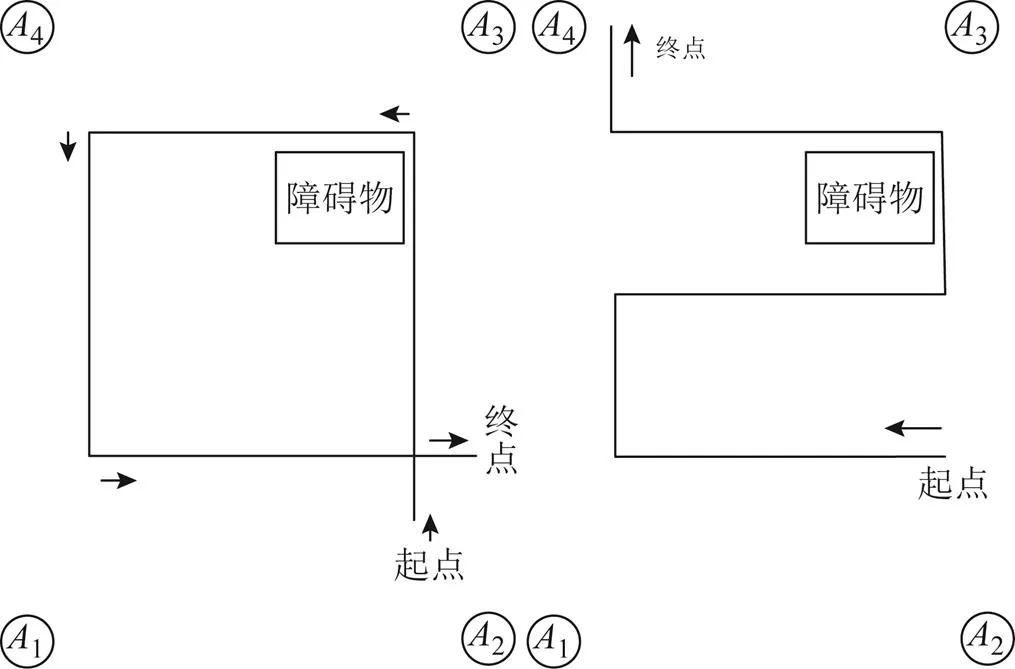
图3 实验场景和实际路径

5.2 数据分析

在上述实验环境中，通过定位系统得到信息，使用最小二乘算法和自适应动量GD-PF算法得到定位轨迹。

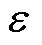
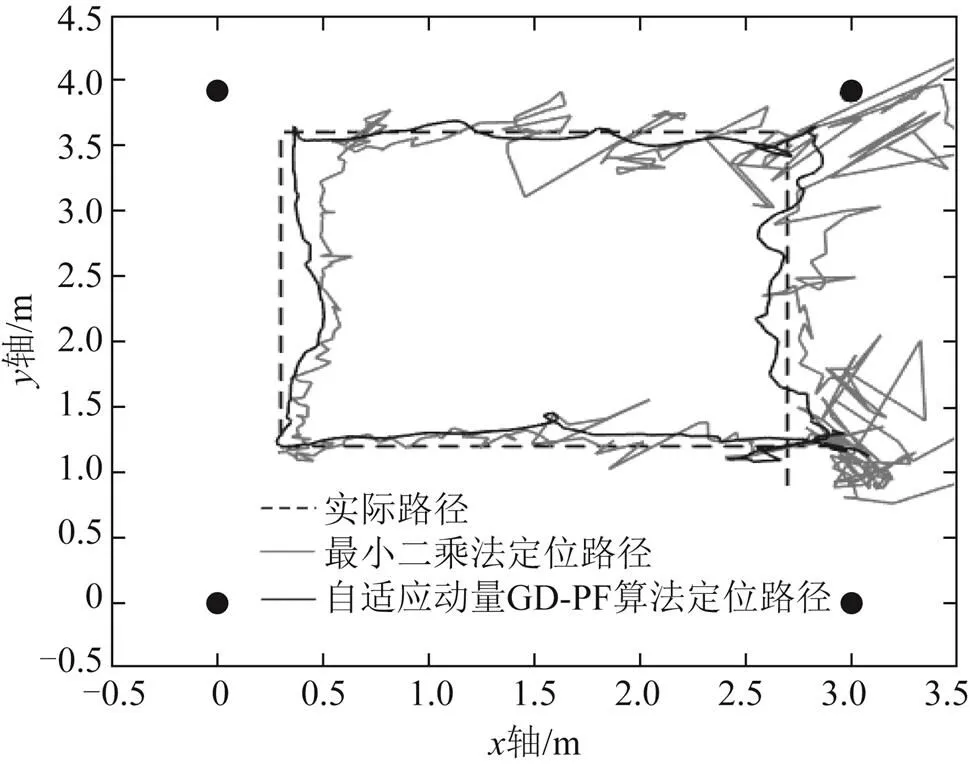
图4 路径1定位轨迹

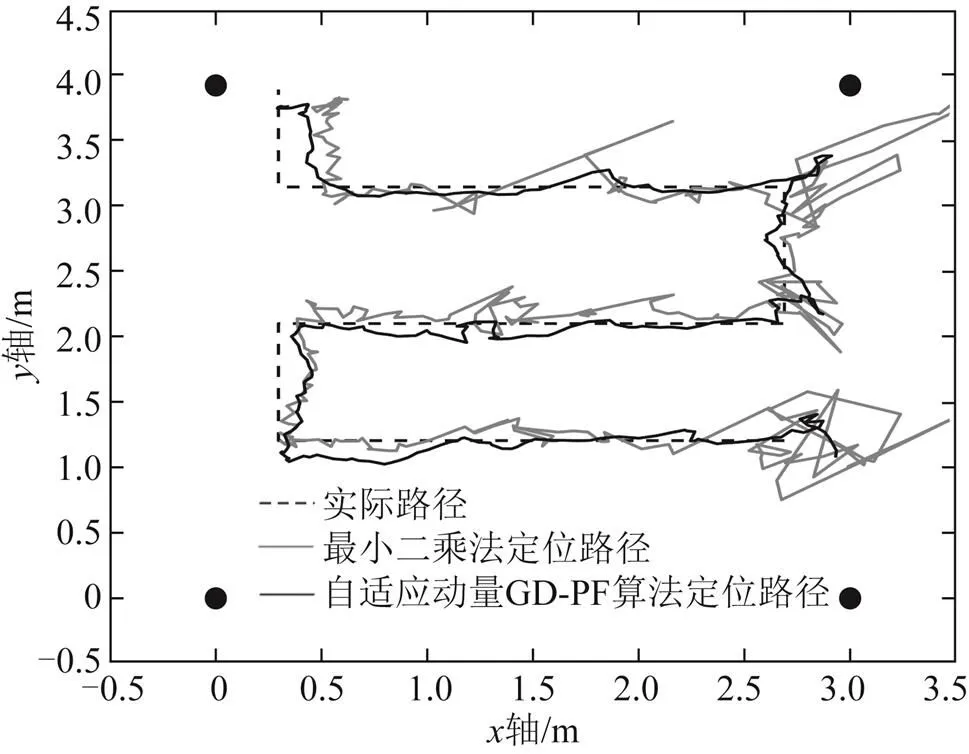
图5 路径2定位轨迹

由图4及图5可知，当前环境下自适应动量GD-PF算法与最小二乘法的定位结果比较，该算法的定位更加接近实际轨迹，也更加平滑，在非视距的环境下的定位更加准确、稳定。

室内定位系统使用不同的算法得到结果的误差。图6和图7为2种路径在最小二乘算法、改进动量GD-PF算法和自适应动量GD-PF算法3种算法下的定位误差比较。

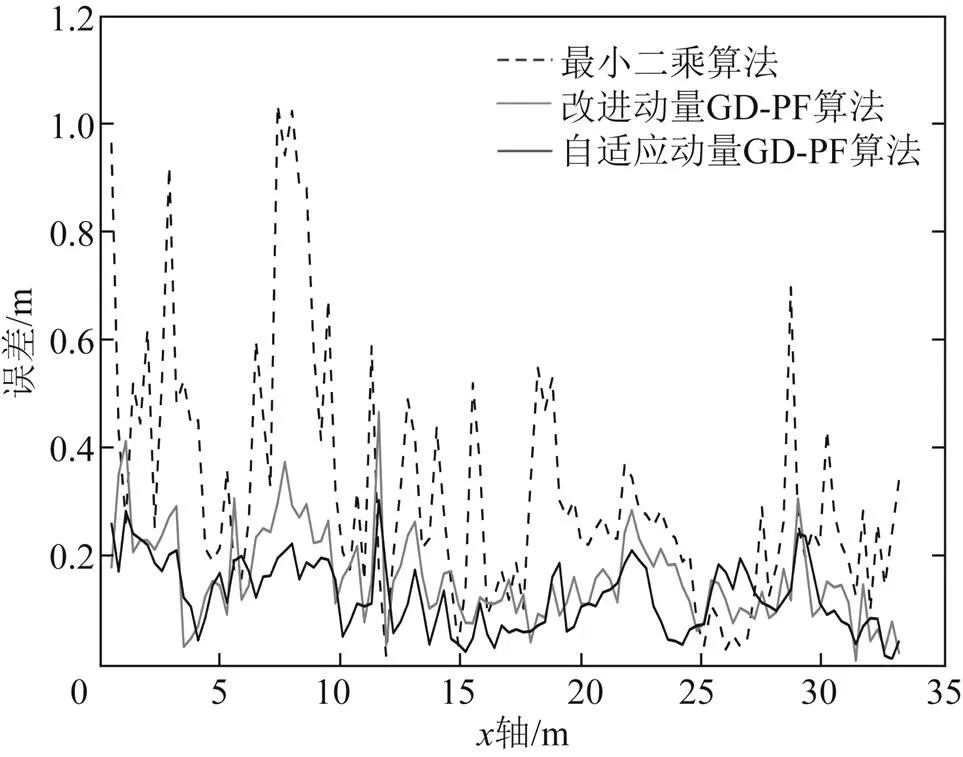
图6 路径1定位误差比较

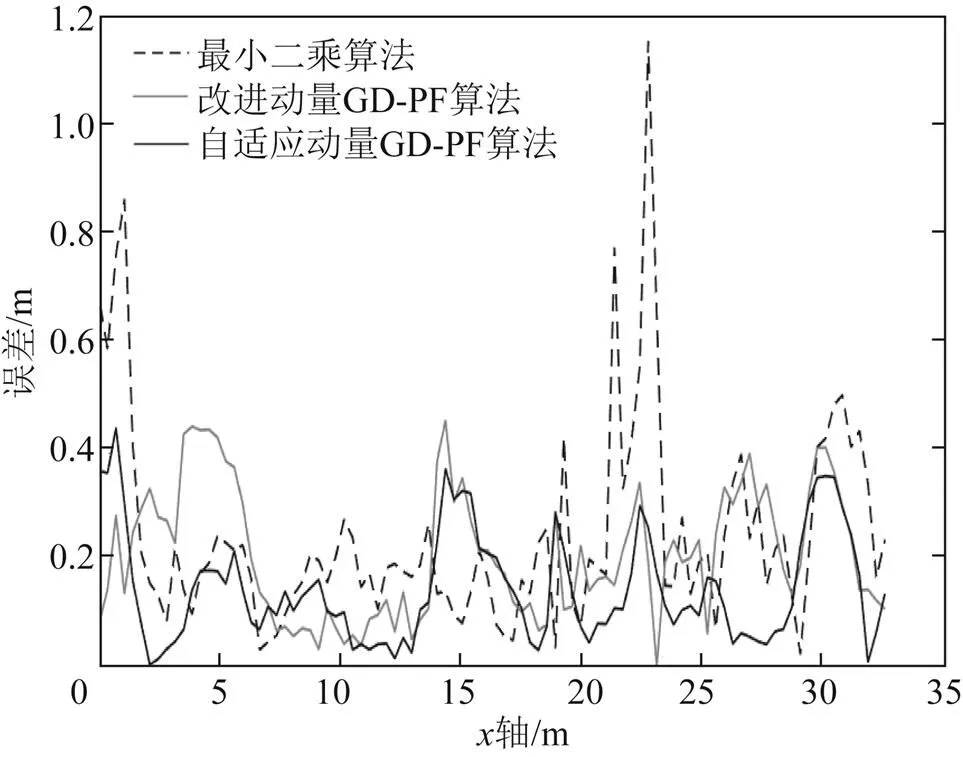
图7 路径2定位误差比较

从图6、图7可以看出，使用改进动量GD-PF算法与最小二乘算法相比，精度都有较大的提升。自适应动量GD-PF算法使用自适应EKF结合MIMU的数据，实现协同定位，该算法得到的定位误差比只使用UWB定位的误差更小，精度更高，异常定位结果明显减少。

表1记录的是采用改进动量梯度下降算法与梯度下降算法的迭代次数的比较。

表1 GD和改进动量GD算法比较 次

路径1需要解算343个位置，路径2需要解算283个位置，由表1可以看出，使用改进动量梯度下降算法的迭代次数比原梯度的下降算法更少。

表2记录的是UWB/MIMU定位在使用不同定位算法的情况下定位结果的误差信息。

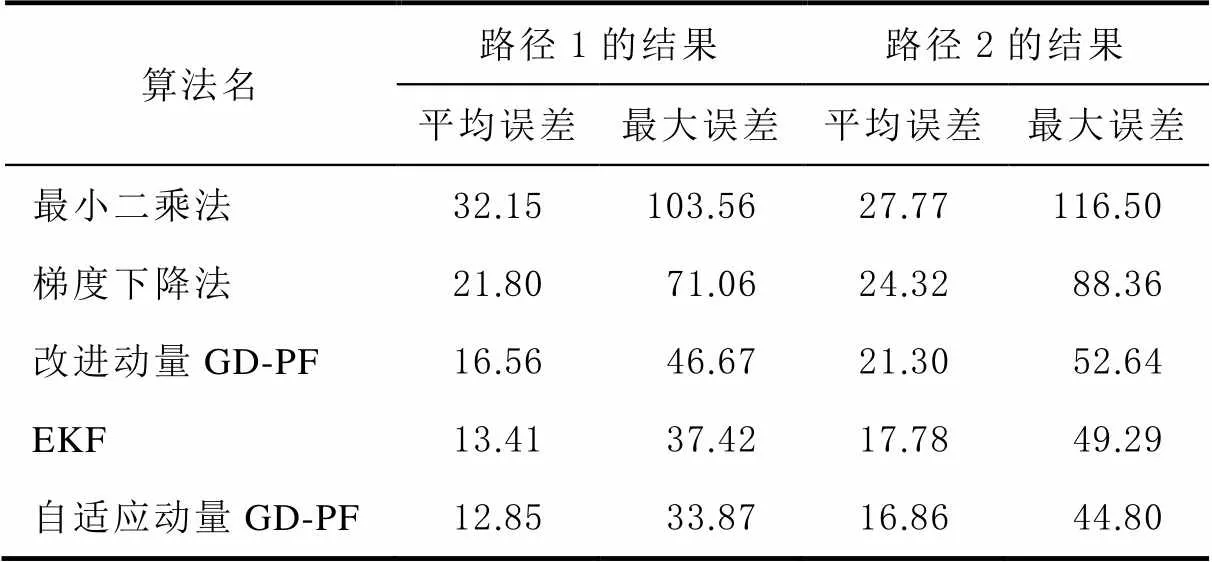
表2 定位误差对比表 cm

从表2中可以发现，梯度下降算法得到定位结果比最小二乘法的更好，使用改进动量GD-PF的误差相较于梯度下降法进一步减小。使用EKF结合MIMU的数据，定位误差又有相应的下降，将EKF加上自适应后，从最大误差值可以发现，相较于EKF，自适应动量GD-PF能够更好地减少异常值的影响，使其定位精度更准确。

6 结束语

针对UWB室内定位在非视距的环境下受环境影响较大的问题，本文提出UWB/MIMU自适应动量GD-PF室内协同定位算法。通过实验和仿真可以看出，动量GD-PF算法与最小二乘法相比，其精度更高，使用改进的动量梯度下降也加快了其位置解算速度。然后EKF结合MIMU的数据后，其定位精度进一步提升，自适应EKF也减少了异常观测值的影响。从而可以得到结论：自适应动量GD-PF算法进行UWB和MIMU协同定位，可以改善非视距情况下的定位效果。

[1] LI Z K, LIU C Y, GAO J X, et al. An improved WiFi/PDR integrated system using an adaptive and robust filter for indoor localization[J]. Isprs International Journal of Geo-Information, 2016, 5(12): 224.

[2] BIANCHI V, CIAMPOLINI P, MUNARI I D. RSSI-based indoor localization and identification for zigbee wireless sensor networks in smart homes[J]. IEEE Trans Instrumentation and Measurement, 2019, 68(2): 566-575.

[3] LI X, WANG J, LIU C. A bluetooth/PDR integration algorithm for an indoor positioning system[J]. Sensors, 2015, 15(10): 24862-24885.

[4] RAMON J R A, FERNANDO S G. Comparing Ubisense, BeSpoon, and DecaWave UWB location systems: indoor performance analysis[J]. IEEE Transactions on Instrumentation and Measurement, 2017, 66(8): 2106-2117.

[5] HU D, HUANG Z, ZHANG S, et al. Joint TDOA, FDOA and differential Doppler rate estimation: method and its performance analysis[J]. Chinese Journal of Aeronautics, 2018, 31(1): 137-147.

[6] 杨天池, 金梁, 程娟. 一种基于TOA定位的CHAN改进算法[J]. 电子学报, 2009, 37(4): 819-822.

[7] BARRAL V, ESCUDERO C J, GARCÍA -NAYA J A, et al. Environmental cross-validation of NLOS machine learning classification/mitigation with low-cost UWB positioning systems[J]. Sensors (Basel, Switzerland), 2019, 19(24): 5438.

[8] ZHAIC, ZOU Z, ZHOU Q, et al. A 2. 4-GHz ISM RF and UWB hybrid RFID real-time locating system for industrial enterprise internet of things[J]. Enterprise Information Systems, 2017, 11(6): 909-926.

[9] KAUNE R. Accuracy studies for TDOA and TOA localization [C]//The Institute of Electrical and Electronic Engineers (IEEE). Proceedings of International Conference on Information Fusion. Singapore: IEEE, 2012: 408-415[2021-05-01].

[10] RUDER S. An overview of gradient descent optimization algorithms[EB/OL]. (2017-6-15)[2021-05-01]. https: //arxiv. org/pdf/1609. 04747. pdf.

[11] 李天成, 范红旗, 孙树栋. 粒子滤波理论、方法及其在多目标跟踪中的应用[J]. 自动化学报, 2015, 41(12): 1981-2002.

[12] 曾庆化, 王敬贤, 孟骞, 等. 基于UWB优化配置的室内行人导航方法[J]. 中国惯性技术学报, 2017, 25(2): 186-191.

[13] 王学斌, 徐建宏, 张章. 卡尔曼滤波器参数分析与应用方法研究[J]. 计算机应用与软件, 2012, 29(6): 212-215.

[14] 沈凯, 管雪元, 李文胜. 扩展卡尔曼滤波在组合导航中的应用[J]. 传感器与微系统, 2017, 36(8): 158-160.

[15] TONG X, LI Z, HAN G, et al. Adaptive EKF based on HMM recognizer for attitude estimation using MEMS MARG sensors[J]. IEEE Sensors Journal, 2017, 18(8): 3299-3310.

UWB/MIMU adaptive momentum GD-PF indoor cooperative positioning

LI Peng, LING Zhichen, RONG Dongcheng, XIANG Yuxiang

（School of automation and electronic information,Xiangtan University, Xiangtan, Hunan 411100, China）

To address the problem that ultra wide band (UWB) indoor positioning is easily affected by non line of sight (NLOS) errors, which leads to a significant decrease in positioning accuracy or even inability to locate accurately. In this paper, an UWB/MIMU adaptive momentum gradient descent-particle filter (GD-PF) indoor co-localization method is proposed. Firstly, exponential weighted average and variable step size strategies are introduced in the gradient descent (GD) algorithm to speed up the gradient solving speed. Then the particle filtering is used to optimize the UWB solved data to reduce the gross errors on the localization accuracy. Finally, an adaptive function is introduced to adjust the extended Kalman filter (EKF) gain to jointly filter the localization data of UWB and miniature inertial measurement unit (MIMU). The experimental results of UWB/MIMU co-localization show that the adaptive momentum GD-PF co-localization algorithm can effectively eliminate the interference of NLOS errors and improve the indoor positioning accuracy and robustness compared with the traditional positioning algorithm.

ultra wide band; miniature inertial measurement unit; gradient descent; particle filter; adaptive extended Kalman filter

TP212；TN925

A

2095-4999(2022)06-0122-07

李鹏，凌智琛，荣冬成，等. UWB/MIMU自适应动量GD-PF室内协同定位[J]. 导航定位学报, 2022, 10(6): 122-128.（LI Peng, LING Zhichen, RONG Dongcheng, et al. UWB/MIMU adaptive momentum GD-PF indoor cooperative positioning[J]. Journal of Navigation and Positioning, 2022, 10(6): 122-128.）

10.16547/j.cnki.10-1096.20220616.

2022-04-11

国家重点研发计划项目（2020YFA0713501）；湖南省自然科学基金项目（2021JJ50126）；湖南省教育厅重点项目（21A0083）。

李鹏（1978—），男，山东青岛人，博士，教授，研究方向为室内外导航定位等。

凌智琛（1998—），男，湖南娄底人，硕士研究生，研究方向为室内导航定位。