基于实验模态的发动机惯性参数识别精度分析
吴 强 李光雪 吴则旭 罗修超
(四川航天职业技术学院 四川成都 610100)
由于发动机等动力设备本身结构的复杂性使得难以通过精确建模或者理论计算得到惯性参数,常常通过实验的手段来估计[1],在实验中需要测量的参数比较多,难免会产生测量误差,因此有必要进行惯性参数识别精度影响因素分析。本文以图1所示的发动机标准块模型为基础,根据激振力位置和方向、加速度响应测试等参数确定各自的误差波动范围,再利用Simulink单层隔振系统数字仿真模型模拟生成一系列加速度响应数据,然后利用仿真数据进行识别计算,根据计算结果分析识别精度影响规律。

图1 发动机标准块尺寸图
1 惯性参数识别原理
本文利用基于实验模态分析方法进行的动力总成惯性参数识别。为建立发动机的振动力学模型,采用了将隔振器安装在发动机下方的形式,不需在发动机机身寻找安装点[2]。在建立模型时作如下假设:发动机本身视为刚体;隔振安装为刚性基础;隔振器简化为三根互相垂直的线性弹簧;发动机的附属连接件不做考虑[3]。由此建立如图2所示的发动机隔振系统力学模型。模型中,为平动坐标系,原点为质心,为静止坐标系[4-6]。
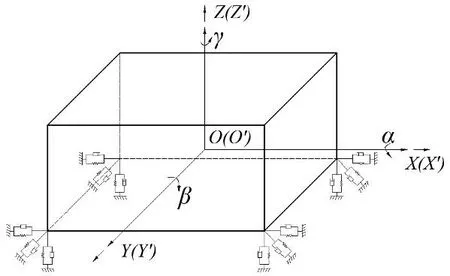
图2 发动机隔振系统一般力学模型
根据牛顿第二定律建立坐标原点处的发动机运动方程为:

式中,M为质量矩阵,C为阻尼矩阵(由于阻尼较小,可忽略),K为刚度矩阵,F为原点O处的广义力向量,Q为原点O处广义位移向量。
将式(1)进行傅里叶变换,得到

根据式(2)得到第p次激励下振动方程为:

假设有n次激励,s个响应点。得到响应点处构成的加速度响应矩阵和n次激励下在原点处产生的激振力响应矩阵分别为:
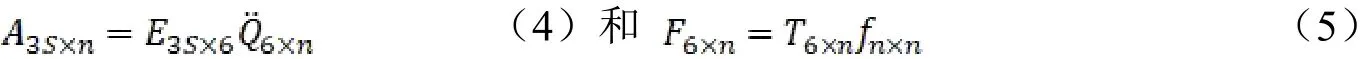
式中,E、T为坐标转换矩阵。
由最小二乘法和式(4)得原点处响应矩阵:

由此,根据式(2)、(5)、(6)可得

将式(7)经过变换可以得到:


2 惯性参数识别程序设计
根据第2节推导的惯性参数识别方法进行编程计算矩阵M,利用MATLAB/GUI开发设计的惯性参数识别程序如图3所示。识别程序主要结合已知数据计算振动微分方程(1)中的质量矩阵M值,再根据公式(10)至(19)计算矩阵M中各元素的关系,从而计算得到10个惯性参数[4]。

图3 发动机惯性参数识别程序
3 惯性参数识别影响因素分析
3.1 激振力位置测试误差
激振点的位置参数直接关系到识别方法中坐标转换矩阵T的值,因此激振点位置测试误差对参数识别精度有着直接的影响。取激振点位置测试误差波动范围为±50 mm(大约为被测对象最大尺寸的10%,工程上可按此比例进行)。将误差波动范围分解为多个误差分析段,以5 mm为误差增量,分别取±5 mm、±10 mm……±50 mm等共10个误差范围段,在每个误差范围内进行100次的模拟计算求得平均值,该平均值反应了在此误差范围内激振点位置测试误差对惯性参数识别精度的影响程度,最终计算得到激振点位置测试误差对惯性参数识别精度的影响结果如图4所示。从图来看,激振点位置测试误差对识别造成的影响不大,最大误差为3.30%,不过对于发动机隔振系统设计而言,惯性参数是进行隔振系统优化设计的重要参数,较小的惯性误差都将使得隔振系统固有频率发生很大变化,所以实验中应该尽量保证激振点位置测试准确。由图4可知,保证激振点的测试误差在±20 mm以内(相当于被测对象最大尺寸的4%,工程上可按此比例参考),可以确保仿真中惯性参数识别误差整体都在1%内,工程上也应该以此为参考,从而获得较为准确的惯性参数。
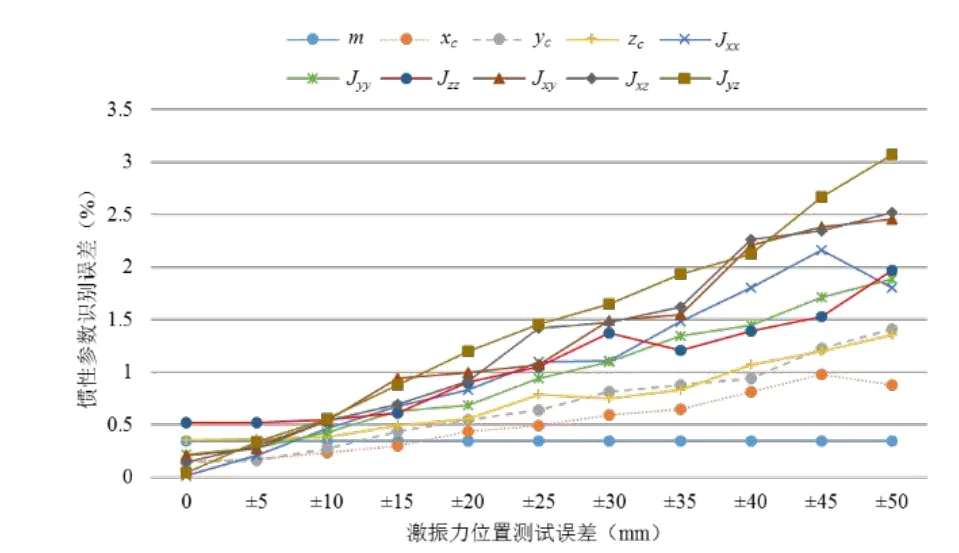
图4 激振点位置测试误差对惯性参数识别的影响
3.2 激振力方向偏差
在计算中认为激振力方向与基准坐标轴方向相同或者相反,而在实际激振过程中并不能保证方向一致或正好相反,而是存在一定的角度偏差。取激振力方向偏差波动范围为±20°。以2°为误差增量,将该范围划分为2°、4°……20°共10个误差范围段,每个范围段进行随机取值计算100次再取其平均值,最终得到激振力方向偏差对惯性参数识别的影响结果如图5所示。由图可知,激振力方向偏差对惯性参数识别精度影响较大,在实验时应减小激振方向与标准方向的偏差角度。由图5知道,如果保证激振方向偏差在±10°以内,可以保证除惯性积外其他惯性参数的识别误差在5%以内。因此在实验中对于某些不能准确掌握激振方向的点可以放弃,从而减小对惯性参数识别所造成的影响。
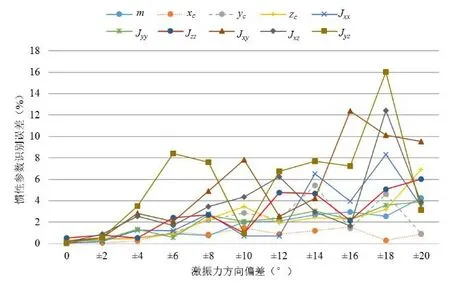
图5 激振力方向偏差对惯性参数识别的影响
3.3 加速度响应测试误差
由于在实验测试中容易受到设备、环境等因素干扰,因此在实验中测得的加速度响应并不是理想的加速度响应。在计算得到的加速度响应上添加误差随机数,从而来检验识别精度。经检验,冲击之后加速度幅值最大值在2m/s2左右,根据工程中的5%经验误差,设加速度响应的误差波动范围为±0.1m/s2。将此范围划分为±0.5%(±0.01m/s2)、±1%(±0.02m/s2)……±5%(±0.1m/s2)共10个误差范围段,在每个范围段内随机取值计算100次求取平均值,最终得到加速度响应测试误差对惯性参数识别精度的影响结果如图6所示。由图可知,加速度响应测试误差对识别精度影响较大,因此在实验中应保证采集仪器的测试精度和采集过程的规范性,如果仪器精度得不到提高,则必须保证人为操作的规范性,比如在测试之前对仪器进行校准、测试中减少周围干扰信号的影响等。
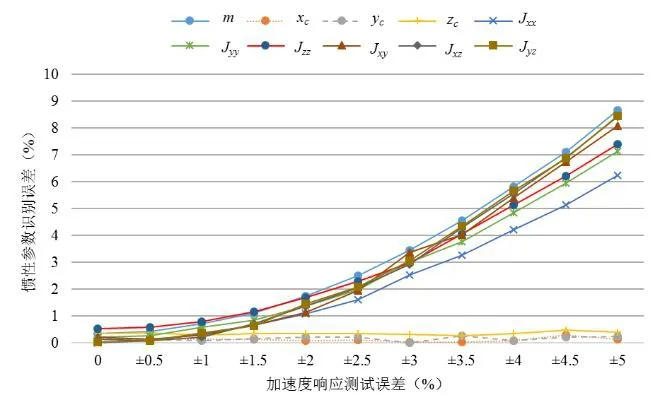
图6 加速度响应测量误差对惯性参数识别的影响
3.4 响应点位置测试误差
响应点的位置参数直接关系到惯性参数识别中坐标转换矩阵E的值,因此响应点位置的测试误差对识别精度有着直接的影响。取响应点位置测试误差波动范围为±50 mm,以5 mm为误差增量将此范围分为±5 mm、±10 mm……±50 mm等共10个误差范围段,然后在每个误差范围内模拟计算100次再求取平均值,最后得到响应点位置测试误差对识别精度的影响结果如图7所示。从图可知,响应点位置测试误差对惯性参数识别精度的影响与激振力位置测试误差对惯性参数识别精度的影响基本一致,虽然在整个误差波动范围内识别误差基本都保持在了5%以内,同前面分析一样,应尽量减小响应点位置的测试误差。由图7可知,应该将响应点位置测试误差控制在±20 mm以内。

图7 响应点位置测试误差对惯性参数识别的影响
3.5 隔振器安装位置测试误差
隔振器的安装位置坐标是计算刚度矩阵K的重要条件,因此有必要分析隔振器安装位置测试误差对识别精度的影响。取隔振器安装位置测试误差波动范围为±50 mm,将该范围划分为±5 mm、±10 mm……±50 mm等10个误差范围段,每个误差范围内进行随机取值计算100次得到隔振器安装位置测试误差对惯性参数识别精度的影响结果如图8所示。由图可知,隔振器安装位置测试误差对惯性参数识别基本没有影响,由此可忽略隔振器安装位置的测试误差对识别的影响。

图8 隔振器安装位置测试误差对惯性参数识别的影响
3.6 隔振器安装角度测试误差
隔振器的安装角度也是计算刚度矩阵K的重要条件,因此安装角度的测试误差也会引起刚度矩阵的实际计算结果。设隔振器安装角度波动范围为±20°,以2°为误差增量,将误差波动范围划分为2°、4°……20°共10个误差范围段,每个范围段进行随机取值计算100次,最终得到隔振器安装方向偏差对惯性参数识别精度的影响结果如图9所示。由图可知,隔振器安装角度偏差对惯性参数识别精度存在一定的影响,不过惯性参数识别误差整体波动范围较小。从计算结果来看,除了对惯性积Jyz的影响稍微大点之外(从0.2%到1.0%),其余惯性参数识别误差基本上都保持在±0.2%以内。在整个误差范围内,惯性参数识别误差都在1.0%内,因此可忽略隔振器安装角度偏差给参数识别带来的影响。
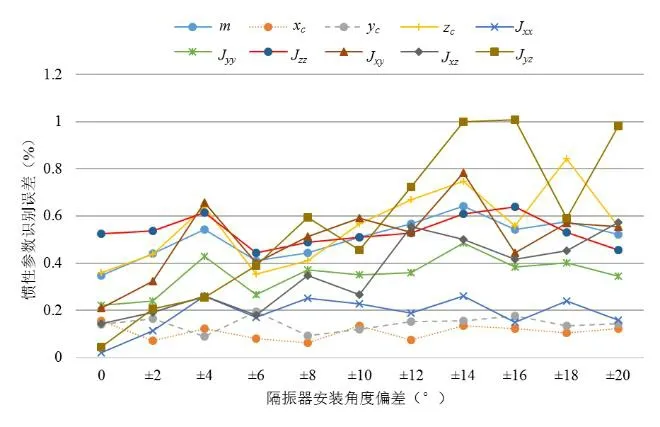
图9 隔振器安装角度偏差对惯性参数识别的影响
3.7 隔振器刚度参数
隔振器的刚度值是计算刚度矩阵K的重要条件,图10是某隔振器实测刚度和设计刚度值,实测刚度值由北京某高分子材料有限公司对隔振器进行动、静刚度测试得到,由图10可知刚度的测试相对误差最大可达15.67%。由此看来有必要分析隔振器刚度变化对惯性参数识别精度的影响,取隔振器刚度误差波动范围为±20%,将此范围分为±2%、±4%……±20%共10个误差范围段。每个误差范围段进行100次随机取值计算,最终得到隔振器安装刚度测试误差对惯性参数识别的影响结果如图11所示,从图可知隔振器刚度测试误差对惯性参数识别的影响很小,结合3.5和3.6小节的分析结果,隔振器安装位置测试误差和安装姿态偏差对惯性参数识别精度的影响也可以忽略,而刚度矩阵K只与这三个参数有关,因此在惯性参数识别上可以忽略隔振器参数测试误差带来的影响。
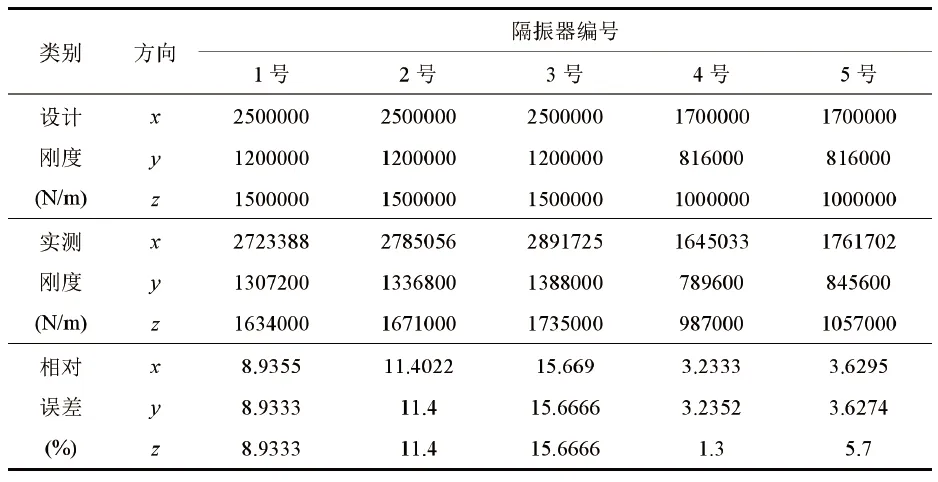
图10 隔振器刚度及相对误差
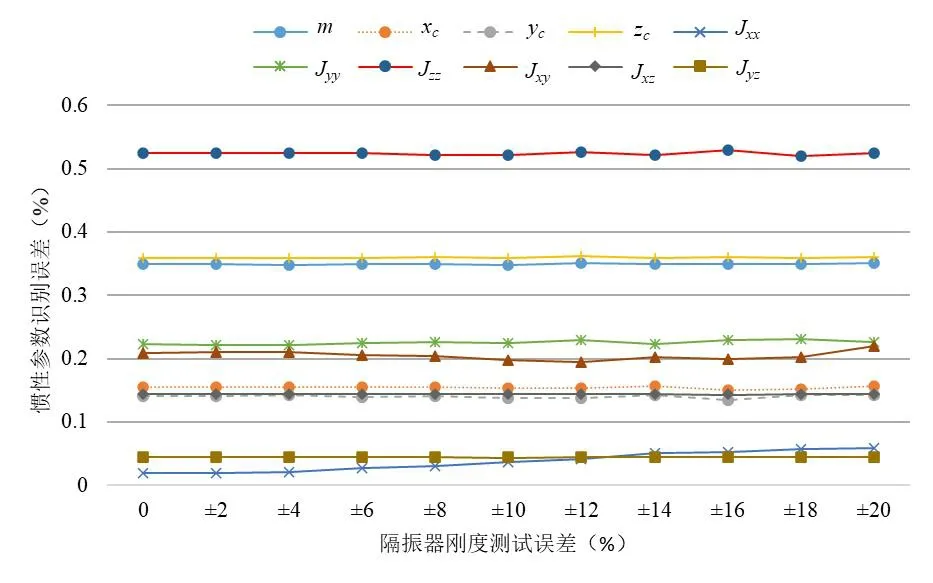
图11 隔振器安装刚度测试误差对惯性参数识别的影响
4 结语
本文详细分析了惯性参数识别精度的影响因素,分别讨论了激振点位置测试误差、激振力方向偏差、加速度响应测试误差等因素对识别结果的影响。主要内容和结论包括:(1)对于激振点和响应点位置测试误差,如果被测对象尺寸大于本文所建立的模型应保证在±20 mm范围内,如果被测对象尺寸小于本文所建立的模型应保证不超过最大尺寸的4%。(2)对于激振力方向偏差,应保证激振方向偏差在±10°范围内,可以保证除惯性积外其他惯性参数的识别误差在5%以内。(3)加速度响应测试误差对惯性参数识别精度影响较大,应保证采集仪器的精度和采集过程的规范性。(4)隔振器参数(安装位置、安装姿态和刚度)对十个惯性参数的识别影响很小,因此在惯性参数识别上可以忽略隔振器参数的影响。

