类AHW助推滑翔飞行器提升气动性能的布局探索
梁海龙 朱目成 唐 伟
(1.西南科技大学制造科学与工程学院 四川绵阳 621010;2.西南科技大学环境友好能源材料国家重点实验室 四川绵阳 621010)
高超声速滑翔式飞行器因具有突防能力强、快速打击和隐蔽性强等特点,备受世界各航天大国关注。20世纪50年代以来,美国十分重视高超声速飞行器技术研发,先后提出了“常规快速全球打击(CPGS)”计划、“猎鹰(FALCON)”计划和“高超声速打击武器(HSSW)”计划等。发展至今比较有代表性的项目包括TBG(Tactical Boosting Gliding),CAV(Common Aero Vehicle),HTV(Hypersonic Technology Vehicle),AHW(Advanced Hypersonic Weapon)等[1]。其中HTV系列借助CAV系列技术研发出HTV-1,HTV-2和HTV-3高超声速飞行器验证机。但是由于美国在高超声速技术方面存在局限性,在2010年先后两次对HTV-2进行飞行试验都未能成功[2]。为继续验证高超声速飞行器无动力助推滑翔技术,美国陆军提出了与HTV-2相似的“先进高超声速武器(AHW)”。AHW作为美国常规快速全球打击众多概念中的一个,2011年11月第一次飞行试验完成了4 000 km的飞行目标,2014年由于火箭发动机故障等因素,AHW升空4 s后发生爆炸,飞行试验失败。2017年海军缩比版AHW飞行试验成功,实现了继HTV-2飞行试验失败之后第一次对高超声速无动力助推滑翔式飞行器的技术验证[3]。
本文以类AHW为研究对象,探索非圆截面布局作为AHW助推滑翔飞行器外形能否进一步提升飞行器气动特性。采用工程气动力预测方法和多目标遗传算法对飞行器关键参数进行优化,重点分析飞行器升阻比和容积率等关键气动特性;在优化分析基础上讨论了不同截面外形的质心位置、边条及舵面布局和尺寸大小、控制舵操纵方式、弹体和控制舵相互匹配等问题;详细分析了不同截面优选质心位置及控制舵尺寸外形的气动特性和俯仰及偏航的配平效率,给出了俯仰控制差动带来的滚转力矩,提供了布局方案。
1 参数化设计及优化
本文根据公开文献[4-5],利用贝塞尔曲线设计生成类AHW双锥十字形小尺寸边条及控制舵飞行器气动布局。为确保弹体轴向外形足够光滑,采用模线设计方法。在飞行器的轴向划分出若干个横截面站位,每一个站位利用贝塞尔曲线形成截面形状,各形状有不同的点控制,利用光滑的轴向曲线连接相邻不同截面的控制点生成弹体外形。其他截面形状可由垂直于轴向的平面与弹体相交得到[6]。
类AHW飞行器作为一种无动力助推滑翔式飞行器,主要目的是实现远程快速到达及弹药精准投送,在飞行器设计中主要表现为升阻比和容积率这两个关键指标。升阻比越大,表示飞行器下降相同高度飞行的距离越远。容积率则代表了飞行器的装填能力。考虑类AHW飞行器布局方式,升阻比主要由弹体产生,弹体几何外形则决定了弹体升阻比。如图1所示,类AHW飞行器外形主要涉及变量为:球头半径R,第一、二锥角θ1和θ2,第一、二锥段长度L1和L2,边条长度Lw,控制舵长度Lk,控制舵高度Lc和尾部直径D等。其中飞行器截面形状(图2)设计主要变量为上半部截面形状设计G、下半部截面形状设计G1和截面短轴与长轴之比ρ。当G=同时控制截面形状时,此时截面为圆截面。
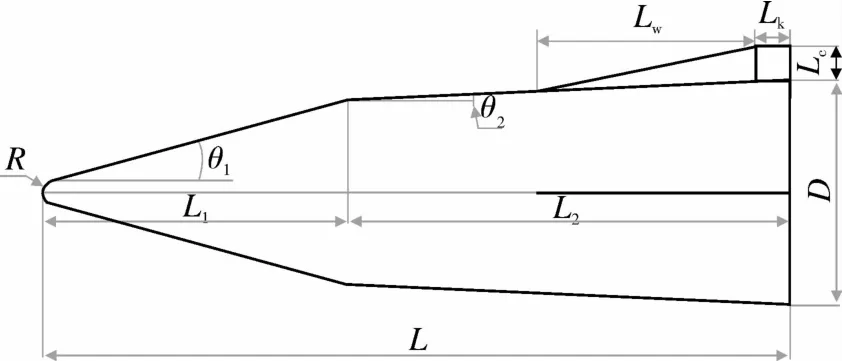
图1 AHW外形参数示意图Fig.1 The parameters of AHW configuration
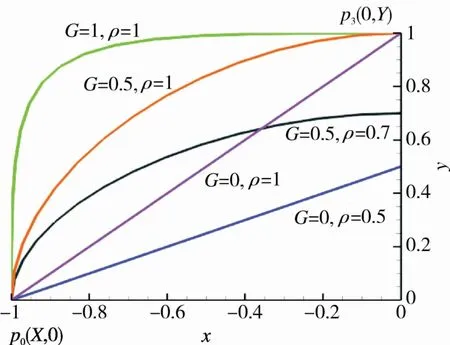
图2 截面参数示意图Fig.2 The parameters of cross section
考虑到类AHW弹体提供主要的升阻比,控制舵更多的是对飞行器进行操纵匹配设计。初步分析只考虑弹体的关键参数影响。作为无动力滑翔飞行器,发射方式一般由火箭推动,但火箭尺寸一般都是固定的,因此飞行器整体长度L和尾部直径D是固定值。那么弹体在设计时,第一锥段和第二锥段涉及到的参数只有两个独立的变量。正交试验设计根据正交性从弹体关键参数全局范围中挑选出具有代表性的参数进行分析,能够极大减少试验次数并获得更多的设计信息[7]。在初步设计阶段,利用正交试验方法对类AHW飞行器弹体关键参数影响进行分析,确定各参数的设计范围。
为预测类AHW飞行器气动特性,本文采用部件叠加法[8],即作用在飞行器上的气动载荷由弹体加上边条及控制舵三者气动载荷相互干扰组成,飞行器气动力系数可表示为:
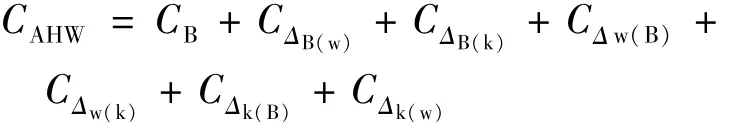
其中:C表示任意气动力系数;下标AHW表示类AHW飞行器;B表示单独弹体;ΔB(w)表示有边条存在时弹体的增量;ΔB(k)表示有控制舵存在时弹体的增量;Δw(B)表示有弹体存在时边条的增量;Δw(k)表示有控制舵存在时边条的增量;Δk(B)表示有弹体存在时控制舵的增量;Δk(w)表示有边条存在时控制舵的增量。
关于单独弹体气动力系数计算,本文采用工程近似计算方法[9-12],该方法利用推广牛顿理论,其压力系数可表示为:

其中:Cp0表示爆炸波压力系数;f(X*,M)表示内伏牛顿理论动压比修正函数;Cpmax表示驻点压力系数;表示物面法向速度;V∞表示来流速度。
多目标遗传算法[13]则是找寻一个决策变量,即设计变量x,使得目标函F(x)达到最优值,其数学表达式为:
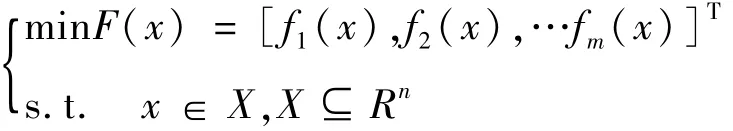
式中:minF(x)代表目标函数F(x)=[[f1(x),f2(x),…fm(x)]T]中的子目标函数都最大程度达到极小化,设多目标优化模型的约束集为X⊆Rn,那么多目标优化时的目标函数为F(x)∈Rm,若有解x1,且x1∈X,如果x1比其他的解都优越,称x1为多目标优化模型的最优解。
根据正交试验方法,利用多目标遗传算法对飞行器弹体关键设计变量优化分析,采用随机遍历抽样、多点交叉和离散变异等方法求解。本文给出的优化模型为:在弹体全长L和底部面积S固定的情况下,寻找在给定的飞行条件下最大升阻比L/D的布局方案,即:Max(L/D)满足约束条件:
(1)全长L和底部面积S固定不变:L=L0,S=S0;
(2)设计变量为飞行器钝度比R/D、第一锥角θ1、第一锥段与全长之比L1/L,飞行器截面上半部形状控制G、下半部形状控制G1和飞行器短轴与长轴之比ρ,其设计区域为:[0.05,5,0.4,0,0,0.75]≤[R/D,θ1,L1/L,G,G1,ρ]≤[0.20,12,0.8,1,1,1];
(3)计算状态:Ma=7,0°≤α≤25°;
如图3所示,利用遗传算法优化分析得出圆截面布局(弹体1)、椭圆截面布局(弹体2)和其他非圆截面布局。表1给出了优化弹体升阻比及容积率分析结果。其中圆截面布局相关文献优化升阻比约为2.2,本文优化升阻比结果为2.180 4,两优化升阻比结果差量仅为0.019 6,对于AHW圆截面双锥体,升阻比优化空间有限。其他非圆截面布局相较于优化圆截面布局,升阻比明显提升,其中椭圆截面布局升阻比提升8.62%,双曲线截面布局提升10.95%。但在改变飞行器弹体截面布局提升升阻比同时,容积率随之减少。优化圆截面外形与正交试验结果相比,容积率下降了3.15%,其他非圆截面布局相较于优化圆截面布局容积率也下降明显,其中提升升阻比性能最大的菱形截面容积率下降17.06%。

表1 弹体优化对比Table 1 Comparison of the optimization of aircraft body

图3 遗传算法优选结果Fig.3 Optimization result of genetic algorithm
因此,为满足设计需求,显著提升弹体升阻比,选取容积率较大的圆截面布局、椭圆截面布局、方形截面布局、双曲线截面布局作为后续研究对象。在当前优化弹体的基础上,给定边条和控制舵尺寸及布局方式得出类AHW飞行器整体外形。如图4所示,后续气动计算和控制舵匹配设计将围绕这几类外形展开。

图4 类AHW飞行器优选外形Fig.4 The optimized shape of AHW analogy aircraft
2 气动特性分析
图5和图6利用工程近似计算方法,给出了优化外形在单独弹体和带舵无舵偏时马赫数7、攻角α范围为[0°,25°]、侧滑角为0°状态下,升力CL阻力CD极曲线变化规律和压心随攻角变化规律。各外形在高超声速范围内零升阻力系数约为0.05,最大升阻比在8°攻角附近。其中圆截面布局最大升阻比约2.18,其他截面布局对比圆截面布局升阻比特性相对增加,椭圆截面布局和方形截面布局最大升阻比约为2.36,双曲线截面布局最大升阻比在2.4附近。各带舵外形与单独弹体相比,升阻比相对增大,说明了设计边条及控制舵能对飞行器提供少量力矩。各截面布局最大升阻比对应较小的攻角,小攻角有利于获得更稳定的配平。

图5 极曲线Fig.5 Curves of lift and drag poles
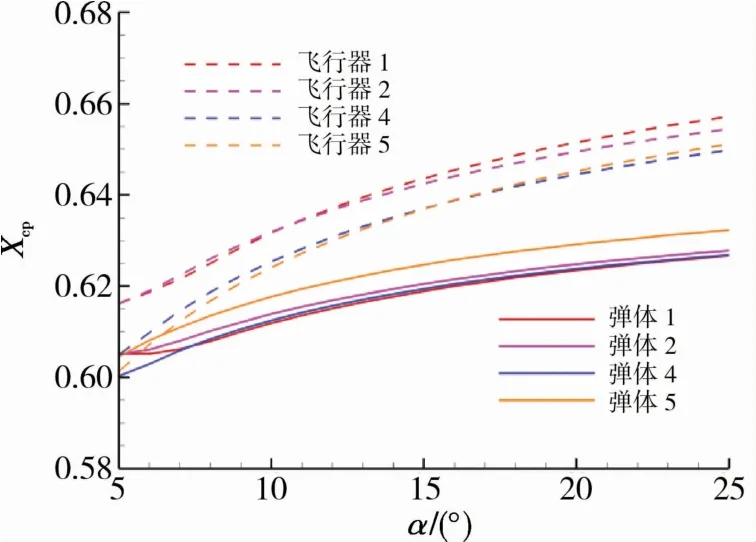
图6 压心特性Fig.6 Pressure center characteristic
从图6压心特性看,相同马赫数下,不同截面弹体布局压心随着攻角增大而后移。在大攻角条件下,圆截面压心最靠前,双曲线截面压心最靠后,椭圆截面和方形截面压心相对靠近圆截面布局。在相同的质心系数下,静稳定度由高到低的顺序为双曲线截面、椭圆截面、方形截面和圆截面。控制舵的存在使得所有截面外形压心后移,圆截面外形压心后移量最大,方形截面外形对比圆截面外形压心更靠前,椭圆截面外形在中小攻角下与圆截面外形压心位置变化不明显,但在大攻角下压心更加靠前,方形截面和双曲线截面外形压心相对圆截面外形较小,在小攻角下,双曲线截面外形压心最小,当攻角达到15°之后,方形截面外形压心最小。这表明各截面外形均能实现正向配平,圆截面外形相对于其他截面布局具有较好的稳定性,而椭圆截面、方形截面和双曲线截面外形则有更好的操纵性。各截面布局满足飞行器稳定性设计,在整个攻角变化范围内压心变化明显,后续配平容易实现。
3 操纵面匹配设计
飞行器在大气层内主要的操控方式是利用伺服机构控制舵面偏转,舵面控制效率好坏直接决定了飞行器飞行质量。控制舵为飞行器提供的气动力矩有限,但对飞行器的力矩特性和配平特性[14]影响较大。想要飞行器在飞行过程中具有较高的控制效率,需要质心设计在弹体压心之后、在飞行器压心之前。因此,在研究过程中需要设计飞行器质心位置和控制舵尺寸。
本文飞行器外形除弹体外,还有边条和控制舵两部分。其中边条的存在使飞行器压心后移,水平方向所受气动力可以看成飞行器的附加升力,提升飞行器升阻比。针对本文研究双锥体高超声速飞行器,控制舵在该类飞行器上的设计方式一般分为全动舵和后缘舵[15]。有舵偏时,后缘舵实现比全动舵小的升阻比损失,但后缘舵在控制舵转时需要伺服机构提供较大的力矩,调节压心能力也相对较小。全动舵布局使得飞行器压心相对靠前,调节压心能力较大,配平能力较强,舵偏对伺服机构的载荷相对较小。结合文献带控制舵双锥体的研究方法[16],考虑体-舵及舵-体干扰等因素,将本文飞行器弹体设置成静不稳定,控制舵采用全动舵设计形式。这种布局可使飞行器偏航和滚转控制时有较高的效率,同时也克服了后缘舵面临的舵偏力矩较大的问题,有效降低控制舵载荷要求。
对于本文研究的小钝度球双锥体飞行器,控制舵舵面布局形式一般有十字布局和叉字布局,文献[17-18]针对锥体外形分析过十字布局和叉字布局的气动特性,相较于叉字布局,十字布局舵面效率、机动配平能力较低,但其控制回路设计简单,舵面偏转角大,航向稳定性强,可调节质心,有利于总体设计。本文选取边条控制舵布局均为十字布局,并讨论控制舵为全动的操纵面匹配设计问题。对于十字布局[19],飞行器俯仰由两水平控制舵控制完成,偏航由两垂直控制舵控制完成,滚转则是由4个控制舵一同控制,或者各控制舵两两差动控制完成。现给定控制舵上、左、下、右舵面偏转角为δ1,δ2,δ3,δ4,并规定以上、下控制舵前沿向左旋转为负舵偏,左右控制舵前沿向下旋转为负舵偏。
如图7所示,采用工程气动力预测方法对带舵飞行器进行气动特性分析,在给定边条尺寸、压心位置和无侧滑的情况下,改变控制舵尺寸控制R(控制舵展向长度与轴向长度之比,轴向长度固定),分析得出圆截面外形、椭圆截面外形和方形截面外形俯仰控制时的舵偏效率。初步设计高超声速滑翔式飞行器时,飞行航程是需要考虑的,设计时飞行器整个飞行过程攻角都需要在最大升阻比附近进行配平,结合图5分析,飞行器的最大升阻比攻角范围在7°~9°附近,因此在设计时最好能实现6°~15°范围内的配平。

图7 配平效率和舵面尺寸Fig.7 Trim efficiency and rudders size
从图7可以看出,相同外形和舵面尺寸条件下,配平攻角随着质心(Xcg)后移而增大,相同质心,配平攻角随着舵面尺寸增大而减小。不同外形之间,相同质心和舵面尺寸,圆截面外形和椭圆截面外形配平攻角比较相近,但总体上椭圆截面外形得到了更大的配平攻角。由于方形截面外形压心位置相对圆截面外形和椭圆截面外形更靠前,所以在配平的过程中获得了最大的配平攻角。
从图7还能得出,圆截面外形质心为0.64,舵面尺寸为0.8时,能实现7°~16°的配平攻角。椭圆截面外形质心为0.64,舵面尺寸为0.8时,能实现6.5°~16.5°的配平攻角。方形截面外形质心为0.64,舵面尺寸为0.8时,能够实现5.5°~21.0°的配平攻角,舵面尺寸1.0时,能够实现5°~16°的配平攻角,并且以上配平攻角均能满足飞行器初步设计要求。
结合图7选取不同外形较好的配平攻角范围对应的舵面尺寸,绘制出不同外形的配平升阻比曲线如图8所示。圆截面外形配平升阻比在2.30附近,椭圆截面外形配平升阻比约为2.45,方形截面外形配平升阻比在2.50附近,最大升阻比攻角范围8°~10°,这时每个外形在配平过程中都得到较优的配平攻角。

图8 不同外形配平升阻比Fig.8 The lift-drag ratio of different shapes trim
飞行器在俯仰方向飞行时,偏航方向需要保持稳定,并且能够进行有效控制[20]。图9给出了3种不同外形布局带舵飞行器俯仰控制及偏航控制共同作用时,攻角及侧滑角配平效率的变化规律。结果显示,各外形配平区间面积接近,随着俯仰舵偏角和偏航舵偏角增大,各外形的控制效率逐渐减小,其中圆截面外形俯仰方向配平效率较高,大于偏航方向配平效率,在相同的偏转角时配平攻角与配平侧滑角接近;由于椭圆截面和方形截面外形布局的非对称性,俯仰控制舵的配平效率比偏航的配平效率高,相同的偏转角下配平攻角明显大于配平侧滑角。此外,偏航配平产生的配平侧滑角直接影响俯仰方向的配平,各截面外形偏航的角度越大,对应俯仰方向配平攻角越小。在相同的偏航舵偏角时,椭圆截面外形俯仰舵偏角攻角斜率大于圆截面外形,控制舵控制效率高于圆截面外形。各外形也可以调节压心位置及控制舵尺寸移动配平区间。
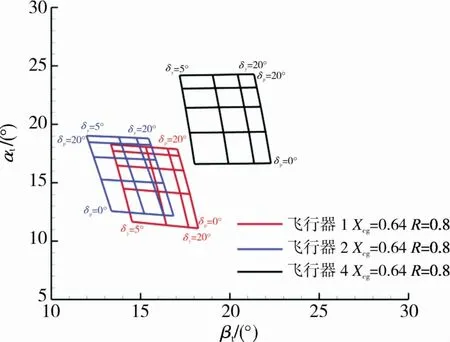
图9 俯仰及偏航配平特性Fig.9 Pitching and yawing trimming characteristics
当飞行器进行空间机动时,攻角和侧滑角不断变化使各控制舵的控制效率出现差异,会产生滚转力矩;同时,飞行器在飞行过程中俯仰、偏航和滚转运动一定会出现交叉耦合,因此飞行器的滚转控制十分重要。图10给出了马赫数7、攻角范围[0°,25°]、不同截面布局飞行器在无偏航控制、俯仰控制舵分别向下偏转5°和10°时,不同舵偏差动角T的滚转力矩特性。俯仰控制舵偏越大,在小攻角情况下,能提供较大的滚转力矩,中大攻角下,较小的舵偏角提供较大滚转力矩。随着俯仰控制舵差动角度增大,各外形滚转力矩先减小后增大。相同条件下,非圆截面外形能够提供更大滚转力矩。在实际飞行过程中,若需要飞行器提供一部分的滚转力矩,可以通过俯仰控制舵差动偏转实现所需力矩。此外,飞行器在俯仰差动时会带来偏航力矩的变化,可以同向偏转偏航控制舵消除俯仰差动带来的偏航力矩,偏航方向达到平衡状态,飞行器实现俯仰差动产生滚转力同时不产生侧滑。

图10 滚转力矩特性Fig.10 Roll moment characteristics
4 结论
本文参考先进高超声速武器(AHW)外形并结合相关研究,利用贝塞尔曲线方法生成飞行器外形,提出非圆截面类AHW气动布局。采用工程气动力预测方法和多目标遗传算法对飞行器进行优化分析,并设计优选弹体质心位置和舵面尺寸。通过对圆截面布局和非圆截面布局外形升阻比、压心进行比较,表明该类以弹体提供主要升阻比的飞行器外形,非圆截面弹身布局方式可以获得更高的升阻比,调整质心位置和控制舵舵面偏转能够实现更高的配平效率,是类AHW助推滑翔式高超声速飞行器实现大升阻比高操纵性的潜在可行方案。

