新能源并网电站涉网性能无功优化方法

卜晓坤

（电力规划设计总院，北京 100120）

0 引 言

在化石能源日渐枯竭的当今社会，新能源已经成为了一种应用范围极为广泛的能源，大量新能源并入电网后却给电网的稳定运行带来了巨大的阻碍。大量的新能源并网电站会导致电网的潮流分布和暂态稳定性变差，进而导致系统原有的运行成本增加，输电系统稳定性降低，原有的继电保护设施难以继续保证新能源并网后的系统性能。为改善并网电站涉网性能，需要对其进行无功优化。通过灵活多变的网络拓扑结构，保证可再生能源对并网电站的支撑作用。优化无功潮流，在降低网损、提高电能质量的同时，对多种可控资源进行调整与控制，进而使所有已经并网的新能源能够获得更积极的消纳路径。文献[1]在分布式电源以及储能系统之间，设计了一种具备恒功率特性的无功优化模型，该模型可以获得更小的计算偏差，同时结合动态均衡方法满足多时段的无功补偿。文献[2]所设计的电力系统在风电、光伏等新能源的加入下，建立了一个新能源电站集群的无功优化模型，该模型使用二阶锥凸松弛算法和分段线性化算法，解决了电压控制不足、系统经济性较差的问题。本文结合上述文献，设计了一种新能源并网电站涉网性能无功优化方法。

1 设计新能源并网电站潮流计算方法

在新能源并网的潮流计算中，首先需要确定不同新能源电源的等效模型。普通异步发电机的并网系统具备结构简单、成本低廉的优点，但是其在工作过程中不具备励磁设备，因此需要通过在发电机一端安装分组电容器的方式进行无功补偿。此时其等值电路可以表示为

式中：Pm表示新能源发电机在等值电路中的发电功率；Im表示电路电流；R表示电路电阻；Up表示电源电压；Qm表示新能源发电机在等值电路中的输出功率；Fs表示潮流计算的转差率；Nx表示转子的有功出力；Nd表示转子的无功出力。在该等值电路下，传统配电网在无新能源时的潮流计算一般使用前推后代法。第1步需要将配电网的平衡节点初始化，此时电压的标幺值可以表示为1 p.u.，且电压的迭代次数为0。第2步开始进行电流的前推，根据计算得到的节点电压以及国内功率损耗，可以结合负荷功率获取全网的功率分布情况，并完成对网络一端的功率计算。第3步需要对回代过程进行处理，在等值网络电路上计算支路功率，结合电压的升降过程，获取节点电压的幅值与相位。前推回代结束后，需要在第4步中检验潮流计算的整个过程是否收敛，通过判断标准确定最终数值是否小于给定值[3]。若没有达到收敛标准，则需要在迭代中循环，直至达到收敛标准为止。在新能源的潮流计算中，需要以上述前推回代为基础，新增新能源节点。不同的新能源类型具备不同的随机特性，其并网方式均不相同，具体如表1所示。

表1的并网方法中，分别列举光伏发电、风能发电、地热能发电、潮汐能发电以及化学电池发电5个类型的新能源并网方法[4]。在新增节点中，需要分别建立新能源的随机特性模型，在此过程中进行等值化处理。在不断迭代下获取电压相量，并计算新能源节点电流的无功功率为

式中：Qm表示DC/AC逆变器作用下电流的无功功率；Qn表示同步发电机作用下电流的无功功率；uk和uk+1分别表示2个紧邻的迭代过程的电压。在该等值化模型下，可以得到新能源潮流计算的具体流程如图1所示。

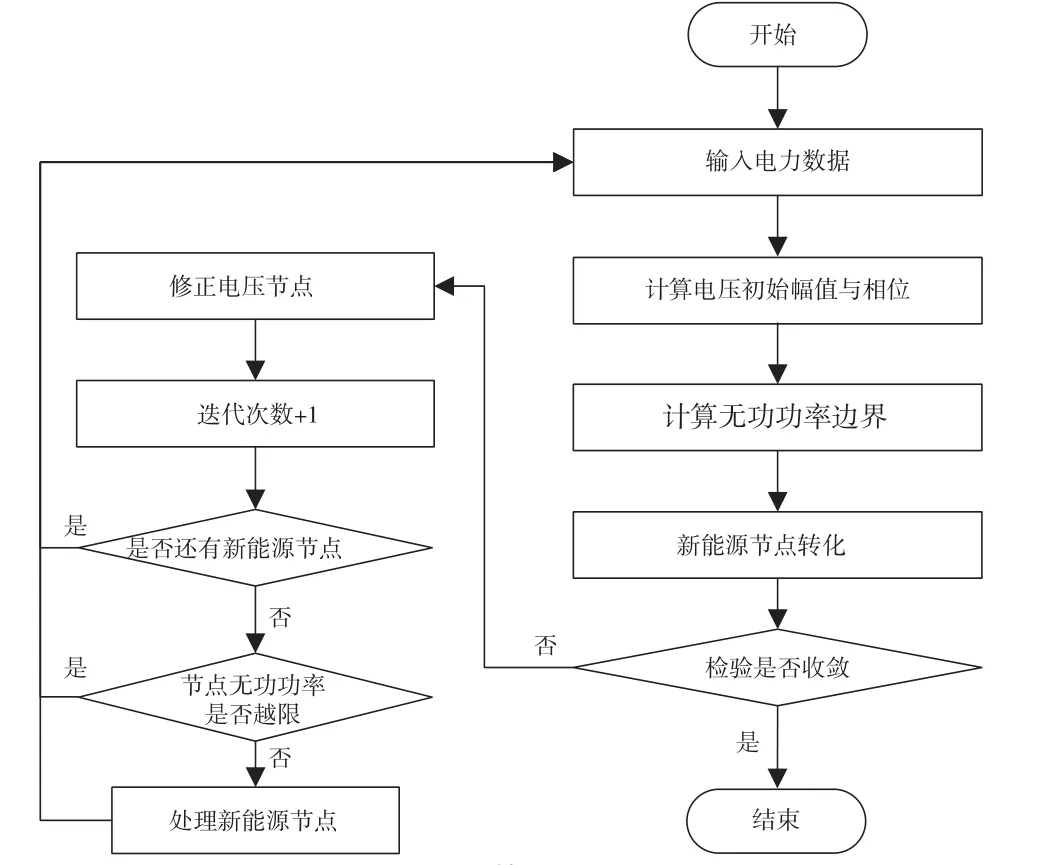
图1 算法流程

图1中，通过是否收敛判断算法是否结束，在此过程中需要使用电压变化量作为收敛标准，其计算公式为

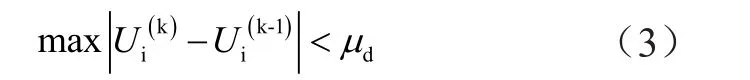
2 建立涉网性能无功优化模型

结合潮流计算的结果，建立涉网性能无功优化模型，需要首先建立新能源接入网络的目标函数。在考虑经营经济性和电压稳定性的同时，依据有功功率损耗的最小值和负荷节点电压偏差的最小值得到目标函数为

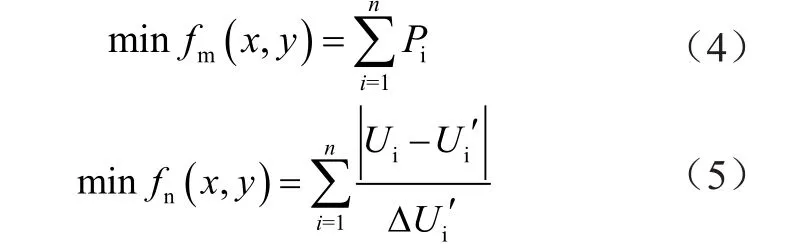
式中：fm(x,y)表示有功功率损耗的函数值；fn(x,y)表示负荷节点电压偏差的函数值；Pi表示有功功率；Ui表示负荷节点上的电压值；Ui'表示负荷节点的电压参考值。在这2个目标函数中，结合不同节点的电压以及有功功率，可以得到约束条件为

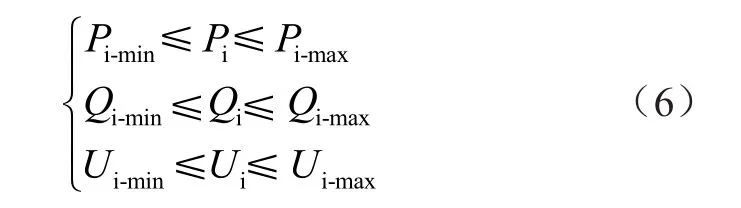
式中：Qi表示无功功率；Pi-min和Pi-max表示有功功率的下界与上界；Qi-min和Qi-max表示无功功率的下界与上界；Ui-min和Ui-max则分别表示节点电压的下界与上界。根据负荷节点的负载电压，可以得到负载电压与传输负载的约束条件为

式中：Vi表示负荷节点的负载电压；Fk表示负荷节点的传输负载；Vi-min和Vi-max分别表示负载电压的下界与上界；Fk-max则表示传输负载的上界。根据上述目标函数以及约束条件，可以对新能源并网电站的涉网性能进行无功优化，并建立一个优化模型[5]。通过有功功率损耗和负荷节点电压偏差，优化并网电站的性能。

3 算例分析

3.1 节点设置

在配电网中，无功功率的影响非常大，本实验对上文设计的新能源并网电站涉网性能无功优化进行仿真分析，并设置一个仿真节点系统。以12节点的链式结构为基础，其系统模型如图2所示。

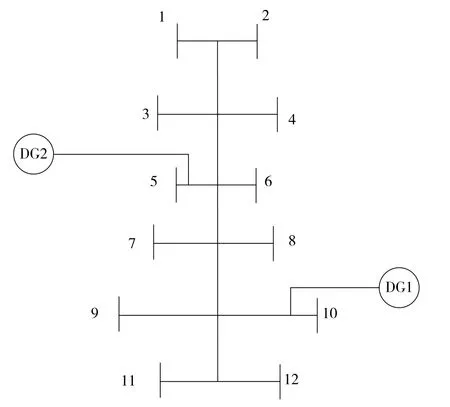
图2 12节点链式结构配电系统模型

在图2所示的配网系统模型中，共存在12个节点，其中节点5和节点10处分别存在1个新能源并网DG。在该系统内，并网DG的有功功率为250 kW，无功功率的范围为0～1 000 kvar。

3.2 2种极端条件下电网工作状态

在上述系统模型中，设定2种极端条件。第一，线路负荷调整为最大值，此时2个新能源并网电源会因为故障或者其他原因而退出工作状态，即此时DG1和DG2的有功与无功功率均为0。第二，线路负荷调整为轻载状态，设定10%功率输出为额定负荷，DG1和DG2这2个新能源系统运行正常，有功出力达到最大，无功出力为0。在上述2个极端条件下，绘制配网节点系统模型的初始电压曲线如图3所示。

图3 初始电压曲线

通过图3所示的仿真结果可知，在条件1中，有一些节点（如节点4、节点5、节点6、节点10、节点11）会越过电压下限。在条件2中，也有少部分节点（如节点5、节点6、节点10）越过了电压上限。

3.3 极端条件优化后效果

使用上述方法对2种极端工况的电压进行优化，可以得到优化效果如图4所示。

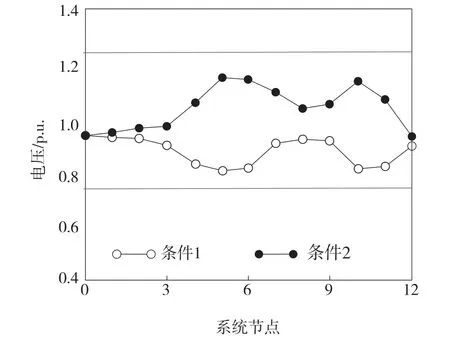
图4 优化效果图

如图4所示，经过优化处理后，2个极端条件下的系统节点电压均在2道界限之间。其中，条件1经过无功优化后的系统电压偏差之和为0.52，条件2的电压偏差之和则为0.88，二者均满足新能源并网电站对电压质量的需求，且本文方法很好地解决了系统节点越过电压上限与下限的问题。

3.4 算法收敛特性对比

设置粒子规模为100，最大迭代次数为700。学习因子a1和a2相同，均为0.5；粒子速度的区间为[-5，5]，惯性权重的最大值与最小值分别为0.8和0.4，分档系数则为300。分别使用本文方法、动态均衡凸-凹步骤法、有功与无功耦合特性方法对上述系统节点进行迭代优化，可以得到适应度函数值如图5所示。

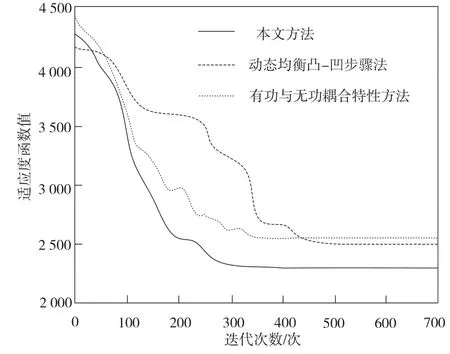
图5 算法收敛特性曲线

如图5所示，在700次迭代中，3种方法均顺利完成了对算法的寻优。其中本文方法在300次时就得到了适应度函数的最优值，动态均衡凸-凹步骤法在500次迭代时寻优结束，有功与无功耦合特性方法则在400次时迭代结束。这3种方法的对比中，本文方法的适应度函数值明显优于其他2种算法。

由此可见，本文设计的新能源并网电站涉网性能无功优化方法能够解决极端条件下的电压偏差过大问题，且在与其他2种方法的对比中，明显性能更好。

4 结 论

电压越限问题一直是新能源并网的重难点，本文设计了一种新能源并网电站涉网性能无功优化方法，该方法可以较好地解决极端环境下的电压越限问题，同时在与其他方法的对比中可知其效果更好。通过该无功优化方法，可以将新能源并网的电压偏差约束在标准范围之内，该范围内的电网电能质量已经能够满足新能源的稳定使用。在接下来的研究中，可以继续使用本文的方法，对串联电抗器进行无功优化，探究冲击电流与串联方式的应用环境，并对算法进行进一步的改进与优化。