计及产业结构和温度因素的神经网络电网负荷预测方法

杨星磊，项川，姜鸣瞻，邓玲，谢琼瑶，杨松坤，谭炜东，路长江

（1.国网宜昌供电公司，湖北 宜昌 443000；2.天地电研（北京）科技有限公司，北京 100083）

0 引言

负荷预测是电网公司的重要工作之一，也是电力规划的第一步，负荷预测的结果很大程度上用于确定电网新扩建的规模和时序。近年来电网公司多次提及精准投资策略，对精益化建设愈加重视，提高近期负荷预测结果的精准性十分重要[1-5]。

至今已经形成多种负荷预测方法，其中趋势外推法可以按照负荷的变化趋势，判定负荷增长趋势，且计算简单、实用性较强，但由于考虑因素单一，预测精度有限[6]。回归分析法利用历史负荷数据，建立回归分析数学模型，但难以处理天气变量等与负荷呈现的非线性关系[7]。时间序列法利用负荷变化的惯性特征和时间的延续性预测未来负荷，但由于没有考虑气象因素和社会因素，预测结果不准确[8-10]。灰色预测法能利用少量的数据建立微分方程模型，对于指数增长趋势负荷具有较好预测效果，但对于非指数趋势增长负荷，预测精度较差[11-12]。

近年来，人工智能与机器学习方法成为计算机科学发展最引人瞩目的成果，该方法可以在不理清各因素之间函数关系的同时，实现预测等目的，具有传统数学方法不可比拟的优势，因此也逐步被应用到电力系统中[13-22]。电力负荷预测逐渐尝试应用支持向量机（support vector machine，SVM）、高斯过程和人工神经网络等机器学习模型。其中，神经网络模型可以表示高度非线性的关系，理论上可近似任意复杂函数，对于负荷预测这种受多种条件影响的预测问题，有较强适用性。基于此，文献[23]构建了一种基于历史负荷数据的神经网络预测模型，在气象、社会因素不发生突变时，可以取得良好的预测结果，但在气象、社会因素变化较大时，预测结果偏差较大。文献[24-30]构建了多种仅计及温度因素的负荷预测模型，但未考虑经济社会因素的影响，在经济社会因素变化时，预测精度不足。

全球变暖的趋势仍在持续，非线性因素中温度、产业结构对负荷预测的影响愈加明显，我国中部、西南等地区夏季高温天气与最大负荷存在一定相关性。本文提出一种计及温度、产业结构等因素的短期负荷预测模型，采用神经网络算法对预测地区的温度和产业结构历史数据进行研究，搭建神经网络结构体系研究各维度间的非线性关系，预测近3 年该地区的最大负荷，预测结果用于引导地区电网公司精准投资和精益化建设。

1 神经网络算法

1.1 基本原理

反向传播算法（back propagation，BP）是现阶段应用最为广泛的神经网络模型，其具有3 层前馈网结构，分别为：输入层、隐藏层、输出层。

输入层为网络与外部的接口，存储输入信息；隐藏层为网络数据处理部分，完成信息的处理与整合；输出层负责将处理后数据结果展示给外界。

BP 网络的核心数学原理为“负梯度下降”理论，即BP 的误差调整方向总是沿着误差下降最快的方向进行，以达到快速收敛目的[31-32]。

1.2 梯度下降与反向传播

机器学习训练的目的就是确定各层连接处权重矩阵的系数，使神经网络模型可以模拟真实情况下各影响因素与因变量之间的函数关系，实现模型与真实情况的高精度近似。常用损失函数表征机器学习对实际情况的逼近情况，损失函数越小，则逼近程度越高。常用损失函数为

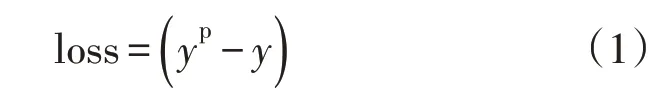
式中：yp为样本的预测目标，y为真实目标。

常用损失函数最小值计算方法为梯度下降算法。该方法通过计算各次参数在当前的参数，然后让参数反向前进适当距离，循环直至梯度接近零时停止[32-33]。

2 基于神经网络算法的负荷预测模型

为提升负荷预测精度，充分考虑经济社会、气象因素对负荷影响，本节将通过设计输入层、隐藏层结构，构建考虑产业结构、温度因素的神经网络负荷预测模型，来预测未来负荷。

2.1 输入层输出层设计

1）确定输入输出维度。

现有神经网络负荷预测方法多考虑历史负荷数据或单一温度因素，未考虑产业结构和温度因素对负荷的综合影响，所以预测精度受限。为充分考虑历史负荷情况、温度、产业结构的综合影响，将神经网络模型输入层设计为三维，分别为历年的最高温度、供电量、二产与三产比值。输出层设计为一维，为以历年统调负荷。维度设计见图1。

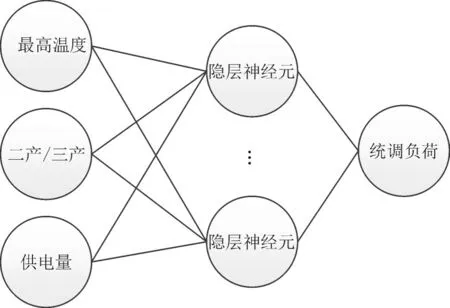
图1 维度设计Fig.1 Dimension design

2）输入数据预处理。

为减少量纲的不同而导致的输入层数值差异问题，须对输入层三维元素归一化或标准化处理。由于输入层变化并不剧烈，仅需归一化处理即可满足需求。归一化公式为

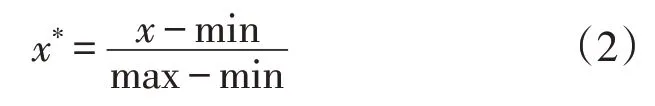
对于最高温度和供电量，可直接根据式（2），利用历史数据最大值、最小值，将最高温度和供电量归一化。二产/三产由于多处于[0，1]区间内，可直接使用，不归一化处理。

2.2 隐藏层设计

1）隐藏层个数设计。

算法计算复杂性与隐藏层个数呈现正相关关系，需综合考虑算法收敛性和计算复杂度设计隐藏层个数[34-35]。应用西南某地区历史数据对单隐层、双隐层、三隐层进行测试，测试结果显示：单隐层的部分组合是可以收敛的，最高拟合度超过0.95，符合预测精度要求；双隐层、三隐层所有组合均不收敛，最高拟合度不超过0.8，不符合预测精度。因此，本次模型选用单隐层的神经网络架构。隐藏层个数测试见表1。

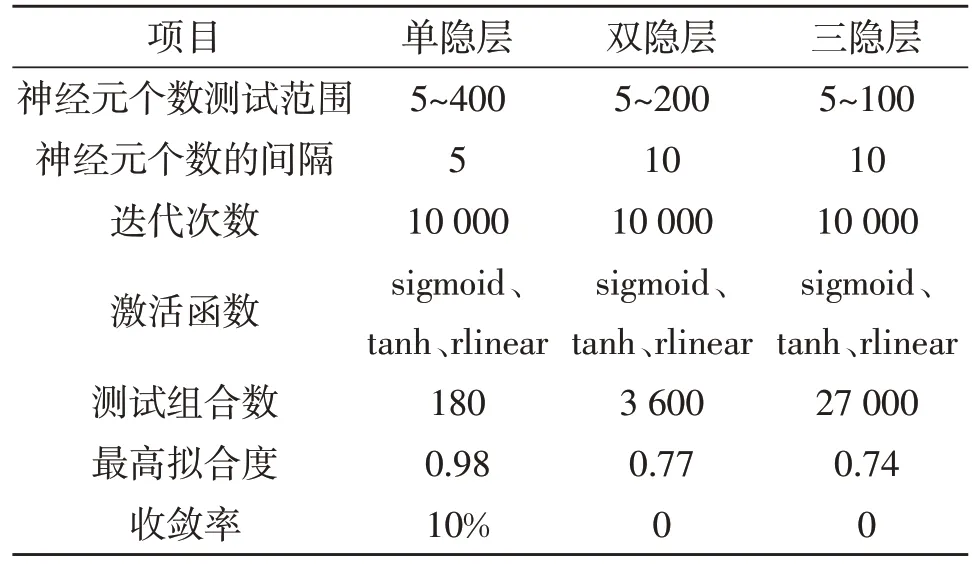
表1 隐藏层个数测试Table 1 Test of the number of intermediate layers

2）隐藏层神经元个数设计。

合理的神经元个数是模型对真实情况模拟程度的保证。过少的神经元个数会导致拟合度不足，过多则会出现过拟合情况。利用历史数据，分4 个神经元数量区间，选用常规Sigmoid 函数进行测试，可以发现：神经元选取200～300 时，训练拟合度和预测拟合度都超过了0.9，训练样本拟合度高，且应用于预测的效果好。因此，本次模型选取神经元个数为200～300 个。隐藏层神经元个数测试见表2。

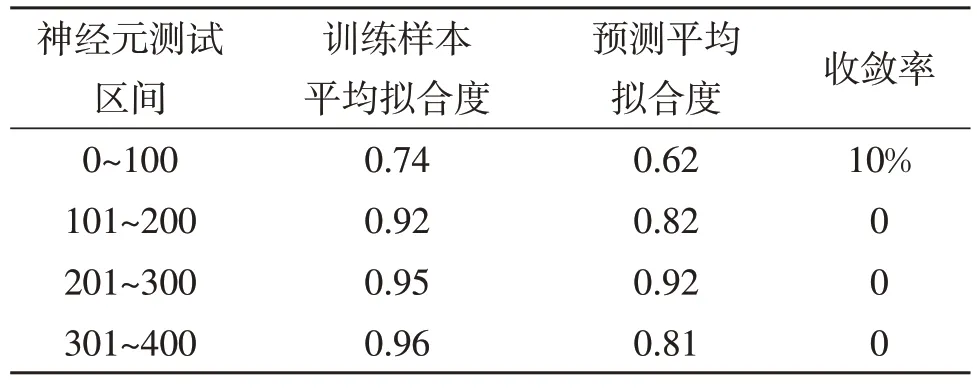
表2 隐藏层神经元个数测试Table 2 Test of number of neurons in the intermediate layers

3）隐层激活函数选择。

激活函数多样，但经过测试，发现仅有Sigmoid函数可以收敛，故选用Sigmoid 函数，作为本次模型的激活函数。

2.3 模型及运算参数

根据前文设计结果，确定神经网络模型输入为1×3 维矩阵，包含12 条记录；隐层设计为3×300 的矩阵，并选用Sigmoid 函数作为激活函数；输出为一维矩阵，选用线性函数作为激活函数。为使神经网络模型与真实情况更加接近，将训练的迭代次数设置为10 000 次，并选用随机梯度下降算法计算损失函数，设置初始权重为0.1。应用SQL SERVER机器学习服务进行模型的运算。预测模型见图2。

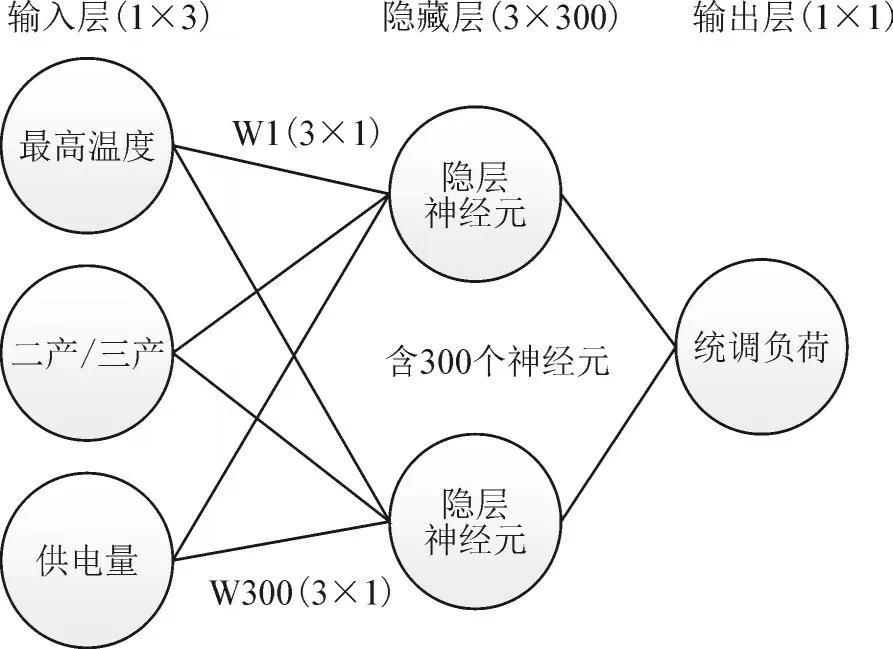
图2 预测模型Fig.2 Estimation model

3 算例分析

应用本文设计近期负荷预测模型，对西南地区某地市最大负荷进行预测。

3.1 精度测试

选择该市2015～2017 年产业结构、电量、温度作为本文设计神经网络的输入层预测负荷结果，预测结果见表3。为展示本文方法在预测精度方面的优势，将本文方法与文献[23]构建的神经网络预测模型进行对比。文献[23]构建模型以前一年电网实际负荷为输入，以预测年负荷为输出，不考虑温度、二产/三产因素影响。

表3 负荷预测结果Table 3 Load estimation results

从预测结果可以看出，较文献[23]预测方法，本文方法预测结果精度优势明显，相对误差不超过1.5%，而文献[23]预测结果误差最大达15.56%。

文献[23]构建的神经预测模型在分别以前一年实际负荷为输入预测2015 年、2017 年负荷时，预测精度虽然较本文方法较差，但处于可接受范围。但2016 年预测结果误差巨大，不具备参考意义。误差出现的主要原因是算例2016 年较2015 年存在明显的最高气温增高、产业结构调整，导致负荷存在较大幅度跃升，而以前一年负荷为输入的神经网络方法难以计及最高温度和产业结构调整带来的影响，只是对历史年负荷增长趋势的合理外推，所以预测结果误差巨大。

3.2 气温、产业结构对负荷影响分析

1）温度对负荷影响分析。

以本文方法，输入层固定二产/三产和供电量，改变最高温度，预测不同温度条件下区域最大负荷情况，预测结果见图3。

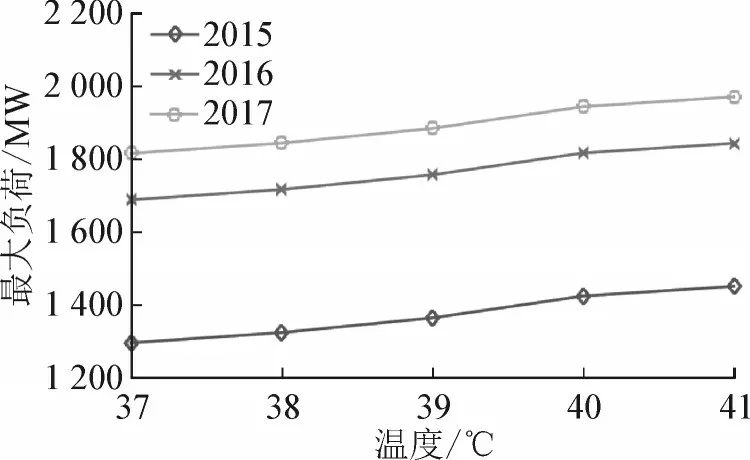
图3 温度影响下负荷预测结果Fig.3 Load estimation results under the influence of temperature

显然，温度升高，区域最大负荷呈现明显增长趋势，其原因多为气温增长导致的制冷负荷增长。由于预测近期负荷时，未来最高气温存在不确定性，可根据历史年数据确定气温范围，预测高中低多个负荷方案，并合理选择。预测结果充分考虑气温因素影响，可根据气温条件制定多个负荷方案并合理选择，是本文方法的优势所在。

2）产业结构对负荷影响分析。

以本文方法，输入层固定最高温度和供电量，改变二产/三产的值，预测不同二产、三产比值下区域最大负荷情况，预测结果见图4。

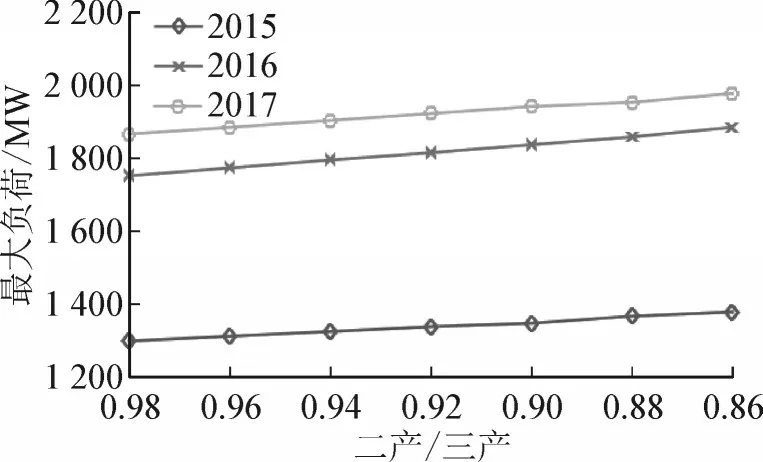
图4 产业结构影响下负荷预测结果Fig.4 Load estimation results under the influence of industrial structure

随着二产/三产比值降低，负荷呈现增长趋势，比值每降低0.02，负荷增长1% 左右。产业结构与当地经济发展水平密切相关，近期各年变化均匀。预测时可根据当地经济发展水平调整，获取更精确预测结果，充分考虑产业结构是本文方法预测结果精准的原因之一。

4 结语

本文针对负荷预测的非线性特性，基于BP 神经网络提出了一种计及产业结构、温度因素影响的负荷预测方法，该方法突破传统预测模型多因素近似线性等效的局限，提高了负荷预测结果的精准性，可灵活分析各因素的影响规律，满足电网公司精准投资和精益化建设的需求。所提预测模型在夏季降温负荷突出的中部和西南部分地区具备广阔的应用前景。