基于改进相关性分析的低压台区拓扑辨别方法
刘学,肖衍,俞乾,谭骏华,何哲
(1.国网湖南综合能源服务有限公司,长沙 410000;2.东南大学网络空间安全学院,南京 210000)
0 引言
智能电网是本世纪初世界电力工业最大的变革和创新,也对智慧城市建设起着制约和促进作用。经过长期的发展,目前国内电力系统基本能够满足经济社会的发展需求,智能电网对智能城市的制约作用并不突出;但智能电网的出现对智慧城市的发展却有着强有力的促进作用,为城市中各大企业提供了优质的发展空间,为市民朋友们提供了更便捷的生活服务[1-2]。
低压配电网(配电变压器台区,简称配电台区)是配电系统的末端环节,直接服务于用户,他的可靠运行是整个电网运行可靠性链条中的重要组成部分,要解决智能电网在发展过程中的关键性问题需要加强对配电网侧的精细化管理[3-4]。然而在低压配电网的管理方面往往仅停留在低电压、超重载和三相不平衡治理等传统问题上[5]。
由于低压配电网结构复杂,缺乏相应的自动化和信息化手段进行网络拓扑异常检测及校验,同时人工现场排查难度大、效率低,导致数据质量较差、更新不及时,进而使得电力信息系统中拓扑物理模型和信息模型及数据不匹配的问题较为突出[6-9]。同时,故障查找及定位依赖于用户投诉或报修[10-11],极大地影响了供电可靠性,以及用户的用电体验。因此,如何通过已有的运行数据建立精准的台区拓扑关系,对实现智能配电台区安全和可靠运行具有重要意义。
综合国内外研究和应用情况来看,校验低压配网拓扑关系主要有人工现场识别(人工方式)和系统自动识别(在线方式)两种[12]。人工方式主要包括工作人员现场清理拓扑,以及使用台区识别仪进行辅助识别。这种方式识别率高,但成本也高,效率低下。在线的方式大多都是是基于低压载波通信技术[13],利用电力线进行信号传输,并在用户端将信号解调为相位信息,实现所属台区和相位的辨别[14]。然而这种方法存在辨识不准确、不稳定的问题,会出现串线情况[15]。
近年来随着我国智能电表的推广和大数据技术的兴起,如何在配电网拓扑识别中运用大数据智能分析方法提高台区拓扑校核的效率成为了一大焦点。常见的方法有基于户变工频过零序列相关性分析、基于户变历史停电事件记录相关性判别、基于多信息相关性分析等[16]。文献[17]基于传统的电网模型无法解决配电网的实际问题的现状,提出了分层的拓扑模型。文献[18]利用电能计量数据与资产数据实现台区用户的识别。文献[19]利用集抄系统的数据进行分析,找出关系异常电表。文献[20]通过在变压器侧注入电压谐波并在智能电表侧进行检测的方式判断户变关系。文献[21]提出了一种利用相位角信息进行拓扑识别的办法,将μPMU 测量相位信息作为主要参数,比较不同拓扑条件下潮流计算得到的相位与实际测量的相位的相关性。这为拓扑识别技术引入新型量测数据提供了思路,但是该方法辨别的准确度和μPMU 设备的精度极其相关,且实际运行中相位数据难以获取。文献[22]通过基于电压曲线相似性的离群点检测方法来校验配电网拓扑,具有一定的应用价值,但无法快速大量地校验某个区域的低压配电网拓扑。文献[6]采用极值点分割时间序列,然后利用电压相似性判别户变关系。文献[12]提出了一种基于皮尔逊相关系数和KNN 算法的拓扑结构校验方法,首先计算用户电压序列曲线的皮尔逊相关系数,并校验台区户变关系的正确性。然后对户变关系不正确的用户进行再校验:基于GIS 系统数据生成用户样本集,运用邻近算法(K-nearest neighbor,KNN)算法对其进行分析,找出其所属的正确台区,最后人工现场校验。这种方法精度较高,但是流程过于复杂,并且依赖于GIS 系统的准确性。文献[23]提出了了基于多维尺度分析(muti-dimensional scaling,MDS)和改进Kmeans 的台户关系辨识方法,该方法首先对电压时序数据进行MDS 算法降维,提取特征,降低计算量,然后采用相关系数作为K-means 算法聚类的标准。这些方法大都利用了电压相似性原理识别户变关系,但在三相相对平衡的情况下,算法准确度难以保证,且无法识别台区内部更精细的拓扑结构。
为此,本文提出基于改进相关性分析的低压台区拓扑识别方法。方法首先根据同馈线上设备的电压相似性,利用基于密度的聚类算法(density-based spatial clustering of application with noise,DBSCAN),尽可能将设备归类到不同的相线区域(A、B 和C),并排除不属于该台区的设备;其次基于能量守恒定律,即上游设备输入功率等于其下游设备功率之和,结合功率皮尔逊相关系数和残差平方和两个因素共同判断上下游设备之间的连通性;最后对设备连通性进行调节,建立最优的台区拓扑结构。
1 低压台区网络结构
如图1 所示,如果不考虑配电表箱下面的用户电表,在低压台区中共有3 类设备:变压器、分支箱、表箱。变压器三相接入一级分支箱并引出多条出线,每条出线下可接多数量的分支箱或表箱扩展并构成台区网络,图中黑色线皆表示三相线缆。因此整个台区拓扑可看作由变压器、分支箱和表箱这3 类设备组成,其中变压器与一级分支箱之间的线路是已知的,故只需识别一级分支箱各出线区域下的拓扑结构。
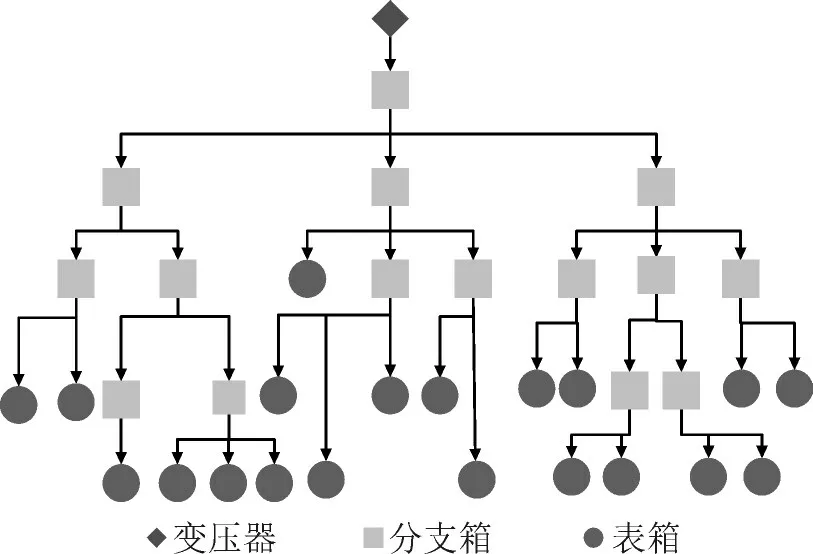
图1 低压台区拓扑结构Fig.1 Topology of low-voltage distribution area
2 低压台区拓扑辨别原理
2.1 电压相似性原理及度量方法
由于同一台区内的电压信号除了具有一定的衰减外,其波形十分相似,但不同台区之间设备的电压曲线波形就存在较大差异[24]。图2 所示为设备电压曲线图,可以看出,台区同出线下设备的电压曲线呈一样的规律波动,保持一定的相似性(即线性相关性),而非本台区的设备,其电压曲线与该台区设备电压曲线就有较大差异,即相似性较低。
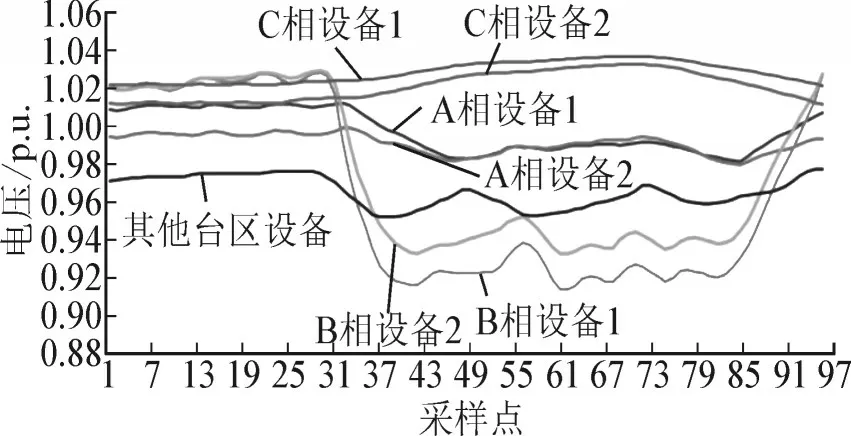
图2 设备电压曲线图Fig.2 Voltage curve of equipment
在电压相似性的度量方面,文中采用皮尔逊相关系数作为衡量标准。皮尔逊相关系数又称皮尔逊积矩相关系数,是用于度量两个变量X和Y之间的线性相关性,其值介于-1 与1 之间。皮尔逊相关系数的定义如式(1)所示。
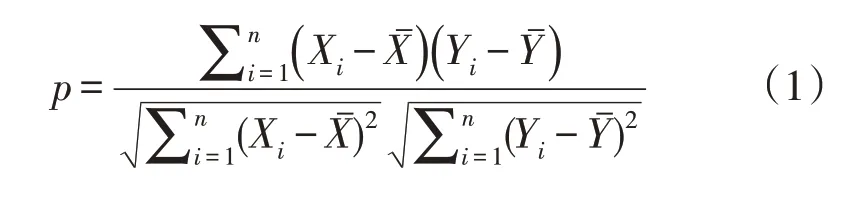
式中:n为样本量;X、Y分别为2 个变量的观测值;Xˉ、Yˉ分别为X、Y的均值。p的取值介于-1 与1 之间,p的绝对值越大,表明变量X与变量Y的相关性越高;p的绝对值越小,表明变量X与变量Y的相关性越低。
2.2 基于DBSCAN聚类算法的设备所属出线区域识别方法
由上述可知,同出线下设备的电压曲线具有极高的线性相关性。图3 所示(以二维为例)为线性相关点的分布及聚类效果,将电压曲线比作空间中一个点,则相关性高的点拥簇在一起,并呈直线分布,相似度低的点分散在周围,因此可以使用聚类的方法,划分出不同出线下的设备及不属于本台区的设备。
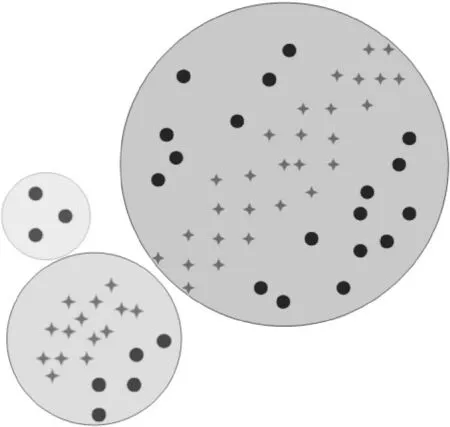
图3 线性相关点的分布及聚类效果Fig.3 Distribution of linearly related points and clustering result
同时在图中也可以看出,若以欧式距离为标准进行聚类,该相关性点将被分隔成3 个类簇,这是因为欧式距离只能识别圆形区域,且属于定量分析,而文中针对电压曲线利用的是定性分析方法。
为此,文中改进了聚类方法的距离标准,改用以点之间的相似距离(皮儿逊相关系数)为标准,进行聚类。距离公式为
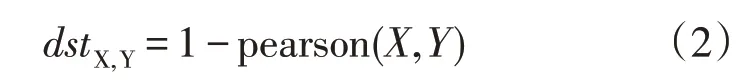
式中,函数pearson 计算变量X与Y的皮儿逊相关系数,计算公式见式(1)。
此外,聚类算法的核心问题是聚类中心个数的确定。由于所选择的设备不仅包含本台区设备,还包含其他台区设备,因为无法实现事先确定聚类中心的个数,故文中采用了基于密度的聚类算法DBSCAN。
DBSCAN 是一种基于密度,且对噪声鲁棒的空间聚类算法。直观效果上看,DBSCAN 算法可以找到样本点的全部密集区域,并把这些密集区域当作一个一个的聚类簇,见图4。其具有以下优点:1)基于密度,对远离密度核心的噪声点鲁棒;2)无需知道聚类簇的数量;3)可以发现任意形状的聚类簇。
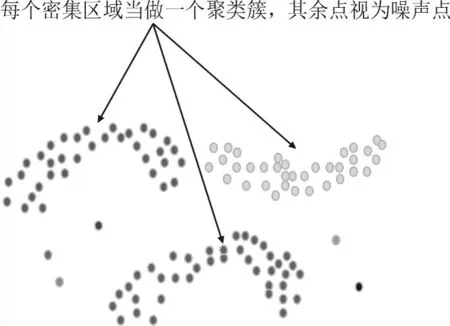
图4 基于密度的聚类示意图Fig.4 Schematic diagram of density-based clustering
该算法需要两个参数:邻域半径R和最少点数目minpoints。当一个点的邻域半径R内点的个数大于最少点数目minpoints 时,该点就是核心点,这片区域就是一个密集。之后,DBSCAN 算法通过合并可合并的密集形成多个类簇,见图5。
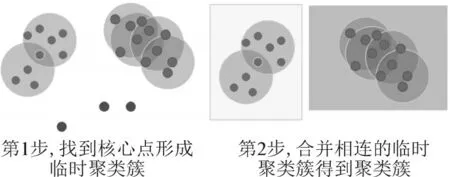
图5 DBSCAN算法的实现步骤Fig.5 Implementation steps of DBSCAN algorithm
同时在图5 中也可以看出,存在个别点不属于任何一个类簇,这样的点就是噪声点,因此DBSCAN算法在对数据进行聚类的同时,也可以实现对异常数据(非本台区设备数据)的检测。
因此文中采用DBSCAN 算法,分别以一级分支箱各出线线路电压数据为标准,将与之属于一个类簇的其他设备都划分至相同的出线区域,单独研究每个区域的拓扑关系,分而治之。其中不属于任何类簇的数据认为是噪声点,即非本台区设备,从研究对象中剔除。
2.3 基于功率曲线相似距离和欧式距离的设备连通性辨别方法
不同分支上的用户存在不同的用电特性,且具有连接关系的上下游设备之间满足基尔霍夫定律和能量守恒定律的约束[25]:上游设备提供的能量等于其下游设备消耗的能量之和。由于客观线损的存在,上游设备的功率曲线和其所有下游设备合成功率曲线会存在一定的差异,但是两者曲线的变化趋势还是趋于一致的,即仍具有极高的线性相关性。如图6 所示相连设备功率变化趋势,具有连通性的上游设备功率的变化趋势与下游设备的合成功率变化趋势基本一致,由于线损的原因使曲线没有完全重合。
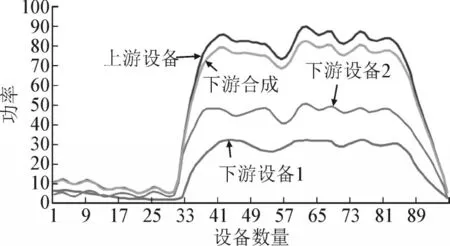
图6 相连设备功率变化趋势Fig.6 Power variation trend of connected equipment
因此可以利用设备之间功率曲线的相关性判别设备的上下游连通关系。
同时考虑到实际运行环境中,电压、功率等数据的采样难以同步的问题,本方法在皮尔逊相关系数基础之上,引入曲线残差平方和参数,采用定性分析与定量分析相结合的分析方法,共同判断设备连接关系。
曲线点之间的残差平方和(SSE)表示曲线之间的差异程度,其计算公式为
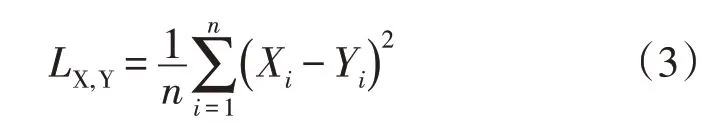
式中:Xi、Yi分别为变量X、Y的采样样本;n为样本个数。
正确的上下游结构应该是满足上游设备功率曲线和其下游设备合成功率曲线相关系数尽可能大、残差平方和尽可能小。因此文中采用残差平方和(sum of squares for error,SSE)与pearson 比值r作为上下游连通性的判别标准,r的值越小,具有连接关系的可能性就越高。
r的计算公式为
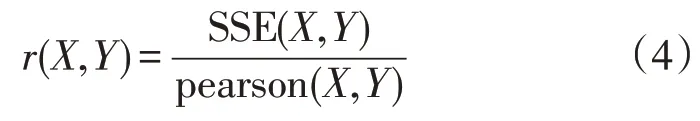
式中:函数SSE 计算变量X与Y的残差平方和,函数pearson 计算变量X与Y的皮儿逊相关系数。
3 低压台区拓扑辨别方法
本低压台区拓扑辨别方法共包含4 个步骤:1)研究对象选择;2)设备所属出线区域识别;3)各相别区域设备连接关系求解;4)区域连通性修正及拓扑生成。拓扑求解大致步骤见图7。
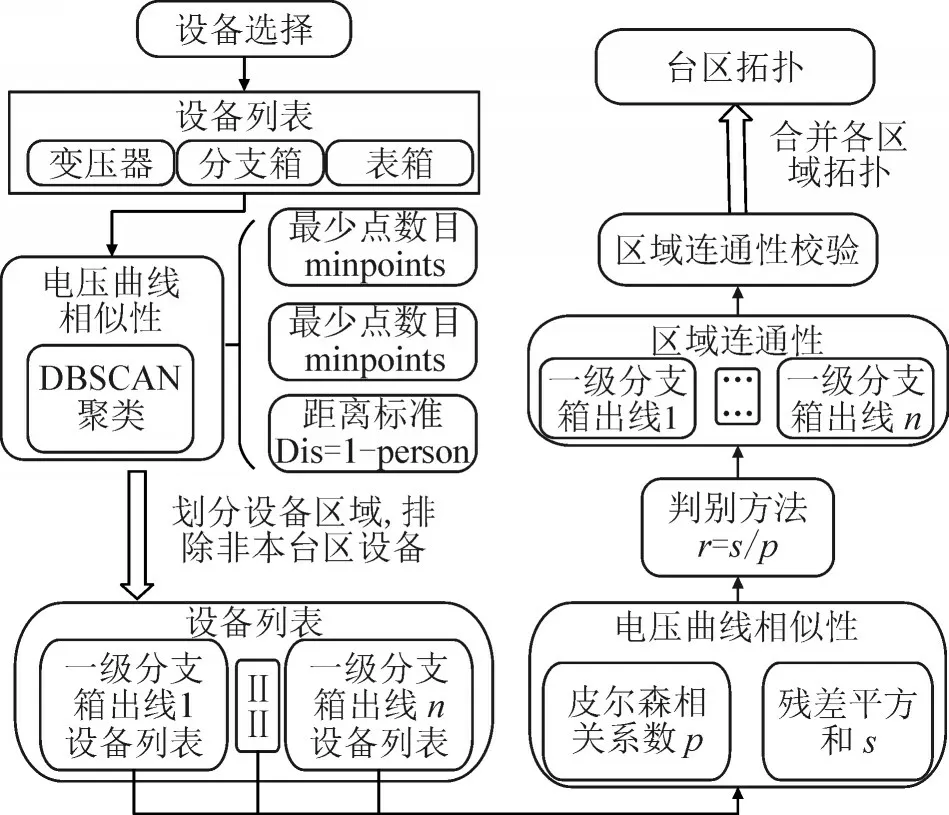
图7 拓扑识别步骤示意图Fig.7 Schematic diagram of topology identification step
首先,根据供电可靠性要求,选择合适范围内的设备作为研究对象,包含所有该台区下设备,且尽可能少的包含其他台区设备。其次基于电压曲线相似性,将不同设备划分至不同的一级分支箱出线区域下,并尽可能地排除非本台区设备,缩小研究范围;再其次基于功率守恒定律,根据SSE 与pearson 比值的判别标准,分别确定每个分支箱的下游连接关系,建立区域拓扑;最后对区域拓扑进行校验、修正,进而建立整个台区的拓扑结构。
3.1 研究对象选择
线路末端的电压会随着线路的增长而降低,且低压配电网输送电压较低,供电线路上将产生较大的损耗,若供电距离过长(即台区配电变压器的辐射范围过大),会造成线路末端用户电压过低,无法满足使用需求[26-34]。
因此根据0.4 kV 的配电变压器供电范围一般要求:供电半径在市区不宜大于250 m,近郊地区不宜大于400 m,农村不宜大于500 m。故文中选择以配电为中心,半径500 m 内的设备作为研究对象,进行台区拓扑识别方法研究。采集这些对象的功率数据,采集的频次每隔15 min 采集一次,采集次数为96 次。
3.2 设备所属一级分支箱出线区域识别
本节目的在于将不同设备划分至其所属一级分支箱出线区域,缩小研究对象范围,步骤如下:
1)根据已知信息,找到一级分支箱R。
2)定义设备集合M表示由3.1 节选择的设备集。
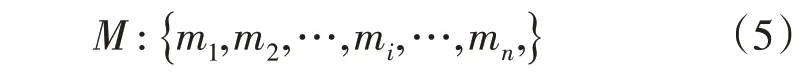
式中,mi为由3.1 节选择的设备,集合M中不包含一级分支箱。
3)分别提取一级分支箱R的各出线电压数据及集合M中各设备电压数据,组成数据集D,n为一级分支箱出线个数。
4)设置参数minpoints。若事先可知各出线下最少节点数size,可设置参数minpoints=size。如若不确定,设置参数minpoints=1,表示允许类簇只包含一个点。
5)设置距离标准dst,见公式(2)。
6)以上述参数minpoints 及距离标准dst,不断调节参数R进行DBSCAN 算法聚类。若在参数R=r下,一级分支箱各出线电压数据点都处于不同类簇;在参数R=r+Δr下,一级分支箱各出线电压数据点出现处于相同类簇的情况,则取参数R=r。此时得到类簇个数c及设备(对应数据集D)所属类别列表cl:{cl1,cl2,…,cli,…,cln,},其中cli表示第i个设备的所属类别编号,若cli=clj,则设备i与设备j同类簇。该参数R确定方法可最大程度上区分各出线下设备,划分出独立的设备区域。
7)分别定义集合A、B、…、J、…、N确定各相线区域下设备列表。
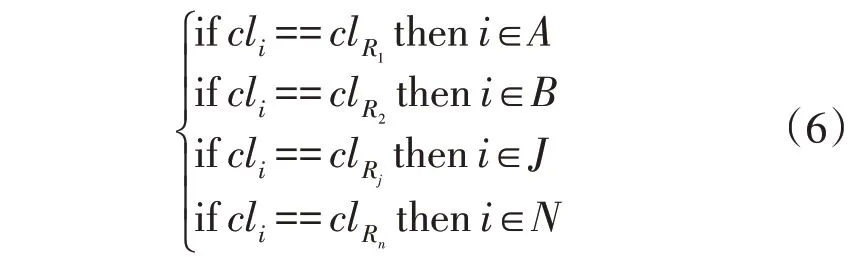
式中:clR1为一级分支箱R的出线1 电压数据所属的类簇;clR2为一级分支箱R的出线2 电压数据所属的类簇;clRj为一级分支箱R的出线j电压数据所属的类簇;clRn为一级分支箱R的出线n电压数据所属的类簇。
8)最后,考虑到聚类效果对后续连通性辨别准确性的直接影响,将其他类簇或噪声点均分别加入集合A、B、…、J、…、N。
3.3 各相别区域设备连接关系求解
本节以识别一级分支箱出线s下设备连接关系为例说明设备连接关系求解一般步骤,并定义集合U,表示已加入拓扑结构的设备集合。关于设备连接关系求解流程共分为两步:1)一级分支箱出线s与其他设备连通性求解;2)其余部分连通性求解。
3.3.1 一级分支箱出线s与其他设备连通性求解
1)依次在集合S中选择选择一个设备mi,其功率数据记为,计算其与一级分支箱出线s功率曲线残差平方和si与皮儿逊相关系数pi的比值ri,具体公式为
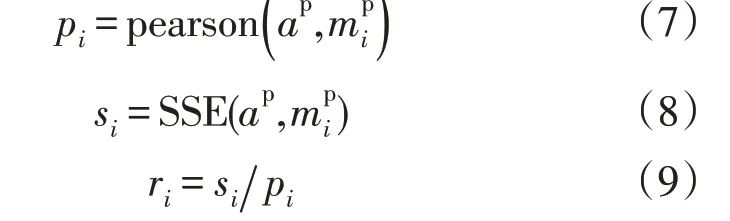
式中:ap为出线s时序功率数据;为设备mi的时序功率数据。
2)判别出线s下连接的设备。如果max(ri),即设备mi是一级分支箱出线s的下游直连设备,将设备mi加入集合U,表示该设备已加入该拓扑结构,并在集合A中将该设备移出。
3.3.2 其他设备连通性求解
1)从集合U中选择一个没有下游连接关系的分支箱x,判断其下游连接设备,其功率时序数据记为xp。
2)根据设备x出线个数k,在集合S中挑选出所有大小为k的子集,记为Si,i表示大小为k的子集个数,i=,n为集合S的元素个数。
3)计算所有子集内设备的合成功率。

式中:为集合Si内设备的合成功率;为集合Si内设备的功率数据;k为集合Si的元素个数。
4)分别计算xp与相关系数pi与残差平方和si的比值ri,判断分支箱x的下游直连设备集合。
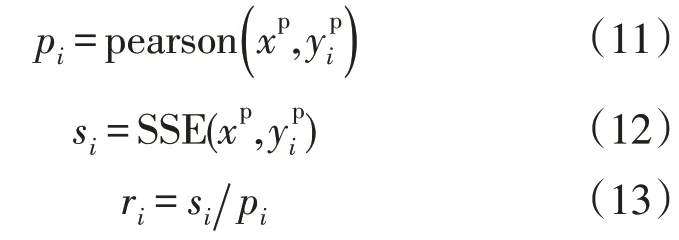
如果max(ri),即表示子集Ai内设备为设备x的下游直连设备。
5)将集合Si内设备全部加入集合U,并在集合S内删除集合Si内设备。
6)重复步骤1),直至集合U的分支箱都明确下游直连的表箱集合。
3.4 区域连通性修正及拓扑生成
通过3.2 节与3.3 为各相线区域所有设备都建立连接关系,但是对于某些拓扑结构而言,该方法会存在一些误判。如图8 所示的部分拓扑结构,由于节点2 只与节点3 相连,因此节点2 功率与节点3功率极其相似,导致节点1 在选择下游设备时选择了节点3,从而导致节点2 没有上游设备,出现拓扑不连续的情况。
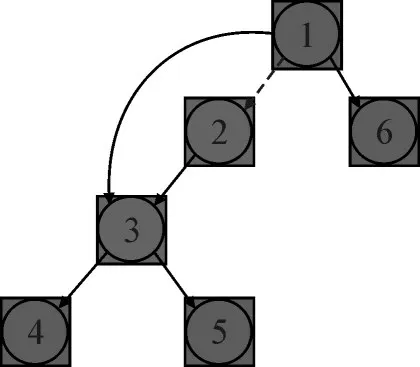
图8 部分拓扑结构示意图Fig.8 Partial topological structural schematic diagram
针对这种情况,可由以下步骤解决:
1)搜索比值矩阵Rp及比值集合(i=1,2,3,…,n)中满足条件的设备mj(mj∈M):使比值矩阵(向量)中值最大的且包含子集设备mj的子集出现一次以上,比如找到了节点3。
2)找到设备mj的上游设备,加入集合E,即将节点2 和节点1 加入集合E。
3)通过残差平方和计算公式,判断集合E中设备的上下游关系。即可判断出节点2 是节点1 的下游设备。
4)更新连接关系。节点1 下游设备集删除节点3,加入节点2;节点2 下游设备集加入节点3。
5)重复1),直至没有满足条件的mj结束。
6)根据新的Rp和,使比值最小项的设备、设备集具有连通关系,基于此完成台区拓扑的建立。
完成拓扑修正之后,以一级分支箱为中介节点,合并三相区域连通关系,建立全网台区拓扑结构。
4 实验结果与分析
本算例欲还原如图9 所示的台区拓扑结构,如图中所示。
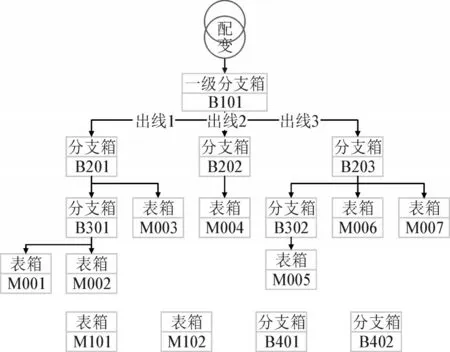
图9 算例台区拓扑结构示意图Fig.9 Topological structural schematic diagram of example distribution area
该拓扑中包含4 个不属于该拓扑的干扰节点(2个表箱及2 个分支箱),拓扑的正确连接关系见表1。

表1 台区拓扑关系对照表Table 1 Comparison table of topological relation of distribution area
数据方面仅模拟并采用单相数据,使用常见的用电曲线初始化终端表箱,进而基于线路阻抗得到全网节点的功率,最后通过潮流计算得到全网节点的电压,并且随机对电压和功率进行±4%的调节,用于模拟采样不同步问题。
本算例共按此方法准备了10 组数据,以下以第1 组数据说明。一级分支箱各相及其他设备的进线电压曲线及功率曲线分别见图10 和图11。
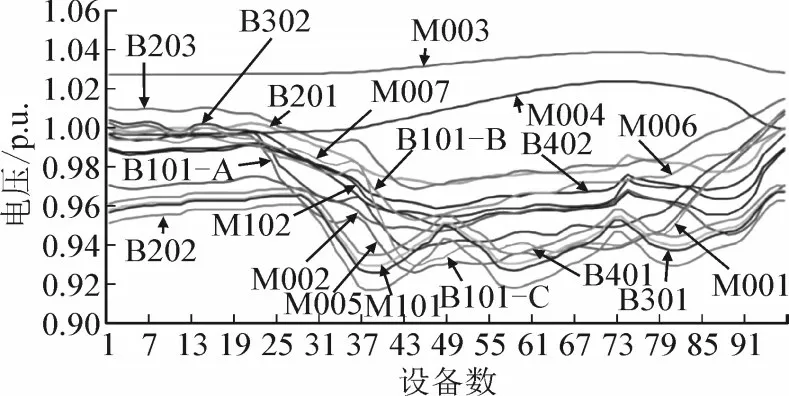
图10 设备电压曲线Fig.10 Voltage curve of equipment
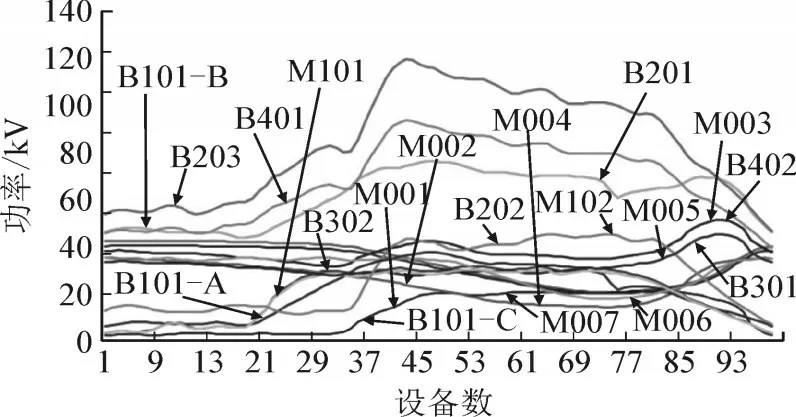
图11 设备功率曲线Fig.11 Power curve of equipment
4.1 基于DBSCAN 聚类算法的设备所属出线区域识别结果
在图10 中可以看出,每相线下至少包含2 个设备,因此可以设置minpoints=3,表示一个类簇至少要包含3 个节点(包含相线数据点)。实验结果分别见表2-4(划线部分为会导致拓扑无法计算的错误分类)。
DBSCAN 聚类结果见表2。由表2 可以看出,当设置R=0.060 时,DBSCAN 共划分了3 个类簇,正好一级分支箱3 条出线电压数据各属于不同的类簇,因此可以划分出3 个区域。但是由于R值的偏小,使出线1 下面的一个设备被当作了非本台区设备;适当放大R值至0.065,如表3 所示,可以准确地将设备划分至其所属出线区域;继续放大R值至0.070,如表4 所示,DBSCAN 共划分了2 个类簇,一级分支箱的出线1 和出线3 电压数据同属于一个类簇,导致没能区分出线1 和出线3 区域,同时也由于R值稍大,将一个非本台区的设备B401划分到了出线2 区域。
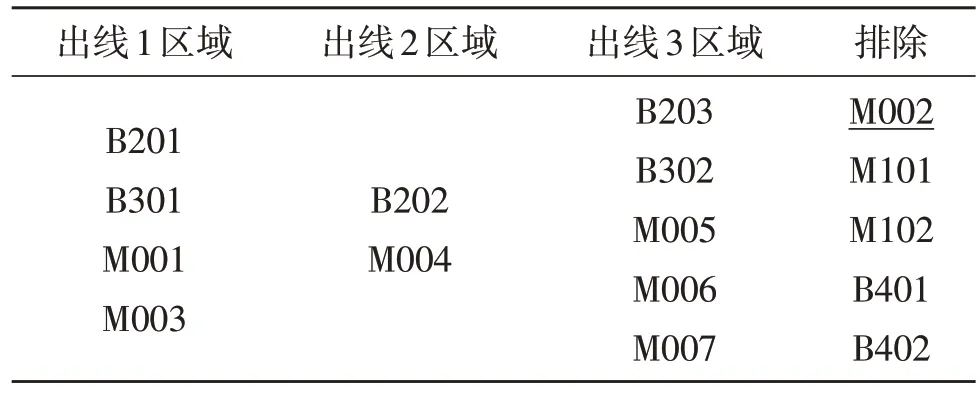
表2 DBSCAN聚类结果(R=0.060)Table 2 DBSCAN clustering results(when R=0.060)
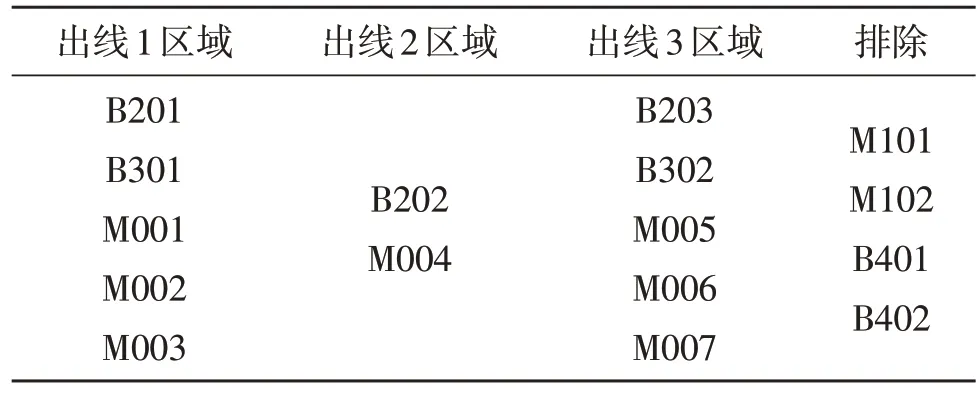
表3 DBSCAN聚类结果(R=0.065)Table 3 DBSCAN clustering results(when R=0.065)
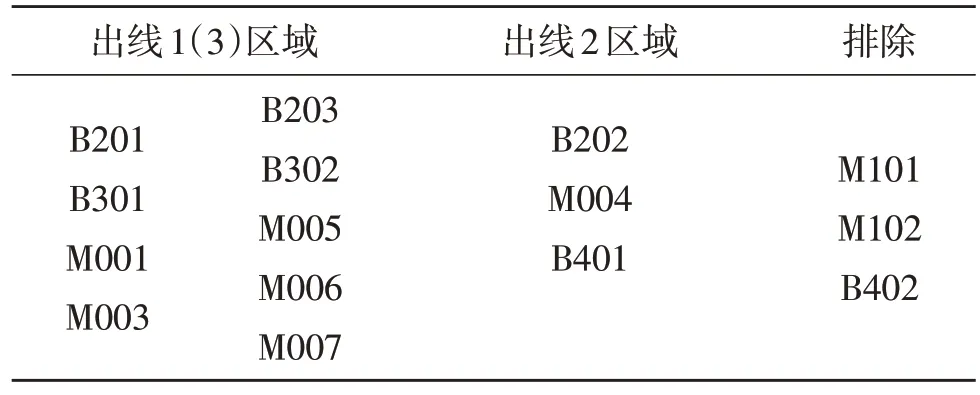
表4 DBSCAN聚类结果(R=0.070)Table 4 DBSCAN clustering results(when R=0.070)
4.2 依据pearson标准判断上下游设备连通性结果
若只依据pearson 标准判断设备连接关系,可以得到拓扑关系对照表(只显示误判部分,划线部分为误判设备),见表5。

表5 台区拓扑关系误判表Table 5 Misjudgment table of topological relationship of distribution area
可以看出,该方法共出现了4 处误判。由于一个设备只有一个直连上游设备,因此一个设备判断错误,必然导致另一个设备判断错误,造成误判的大量出现。
4.3 根据功率曲线相似距离和欧式距离的设备连通性辨别结果
若依据SSE 和pearson 比值标准判断设备连接关系,结果见表6(划线部分为误判设备)。

表6 SSE 和pearson比值判别标准Table 6 SSE and pearson ratio discrimination standard
从表6 可以看出,该判别标准修正这大部分错误,但是出现了3.4 节所描述的相关误判。利用3.4节方法进一步修正,可得到同表1 相同的正确的台区拓扑关系。
4.4 全部算例统计结果
首先,仅采用pearson 标准判别时,10 组数据连通性判断结果统计见图12。

图12 pearson判别标准Fig.12 Pearson discrimination standard
可以看出10 组数据中共出现了24 次线路误判,准确率约
最后,采用SSE 与pearson 比值标准判别时,10组数据连通性判断结果统计见图13。
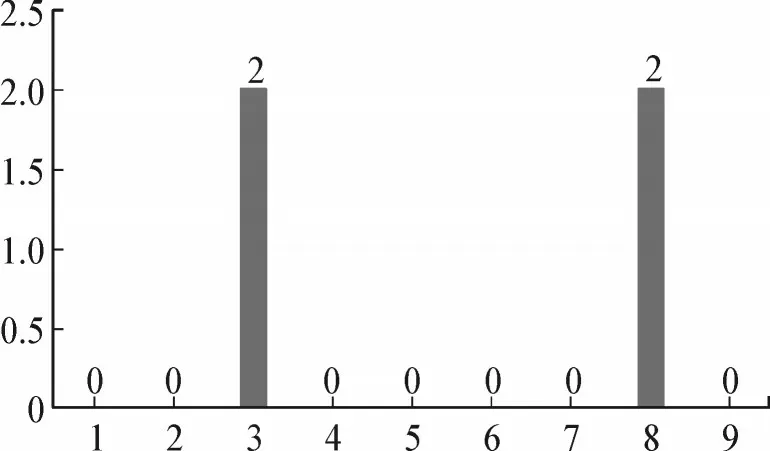
图13 SSE与pearson比值判别标准Fig.13 SSE and pearson ratio discrimination standard
5 结语
针对低压台区拓扑不明,档案信息不准确等问题,文中提出了一种基于改进相关性分析的低压台区拓扑识别方法
首先,基于同馈线设备的电压曲线相似性对设备进行划分。文中采用的DBSCAN 算法既可以将电压曲线相似度高的设备聚为一类,又可以识别出不属于本台区的设备。同时文中针对参数R的设置方式,最优的将本台区设备划分不同出线区域,通过划分设备的方式分解了问题,为后续的连通性识别的快速和准确奠定基础。
最后,基于能量守恒基本原理,采用定性分析和定量分析相结合分析方法,综合考虑设备功率曲线的相关系数和残差平方和,共同判断各区域设备的上下游的连通性,在一定程度上降低了由于数据采样不同步带来的影响,提高了识别准确性。同时检查各区域设备连通性,对冲突节点进行了修正,进一步完善当前区域拓扑关系,进而建立准确的台区拓扑结构。
算例结果分析表明,文中提出的识别方法能够准确识别台区拓扑结构。

