富硒绿茶电磁理条线圈结构优化设计与温度均匀性分析
桑 普,陈 成,王 诚,王书范,廖红华
(湖北民族大学 智能科学与工程学院,湖北 恩施 445000)
理条是富硒绿茶加工过程中的重要环节,理条温度的大小与均匀性,决定着富硒绿茶加工品质的优良性和茶叶中硒元素的含量[1].将电磁加热技术应用到富硒绿茶加工领域,可以使理条机具有升温快、温度均匀性好、噪音小、节约能源等优点[2].
程方平等[3]通过分析现存理条机的研究状况和发展趋势,提出现存的理条机有噪音较大、振动大、热损失大、受热不均匀等问题.邓雪[4]从电加热和红外加热方面对理条加热温度的均匀性进行了分析,提出改进方案,但与电磁加热方式相比,能源消耗大、温度均匀性调控更繁琐.王宏民等[5]采用电磁加热的方式,从电流强度、频率等因素对有效加热区域内的加热盘温度均匀性影响进行了仿真分析.结果显示,电流强度和频率对加热盘温度均匀性有不同的影响.富硒绿茶电磁理条需要对整个金属导热层的温度均匀性进行仿真分析,而不仅仅是对有效加热区.
通过对富硒绿茶电磁理条线圈结构进行优化,设计出4种结构的单一线圈模型,在COMSOL软件中进行模拟,通过改变线圈中的电流强度、频率以及金属导热层与线圈的间距,分析其对金属导热层温度均匀性的影响,从而控制影响因素,进一步提高温度均匀性.最后,建立符合11槽富硒绿茶理条机尺寸的电磁加热模型并进行仿真分析.
1 数学模型构建
1.1 电磁场有限元计算数学模型
在富硒绿茶电磁理条机中,电磁加热装置的原理依据法拉第电磁感应定律:通电线圈产生交变磁场,金属导热层切割磁感线产生涡流效应,涡流使得金属导热层底部载流子高速无规则运动,与原子相互碰撞、摩擦产生热能[6-7].因为金属导热层电阻率大,热转化率高,温度迅速升高,达到加热的目的.
根据Maxwell方程组,可以得到微分形式的涡流场方程组:
(1)
式(1)中:向量H表示磁场强度,向量J表示电流密度,向量D表示电通密度,向量B表示磁感应强度,向量E表示电场强度,ρ表示电荷密度.∇为梯度算子.引入矢量磁势A和标量电势φ与电势得定义:
(2)
再将式(2)中的B和J带入式(1)中,则可得到磁势方程:
∇(1/μ)(∇×A)=-σ(∂A/∂t)+J0.
(3)
式(3)中J0为线圈电流密度.式(1)~(3)在空间中任何一点均成立.
同时,必须考虑在介质影响时的情况,引入对B、H、J、E、D的约束方程:
B=μH,
(4)
J=σE,
(5)
D=εE.
(6)
式(4)~(6)中:μ表示磁导率(H/m);σ表示材料电导率(S/m);ε表示介电常数(F/m).
在COMSOL仿真过程中,需要考虑金属导热层表面集肤效应的影响,即金属导热层在不同点处所产生的电流密度值有所不同,由外向内衰减,如图1所示.
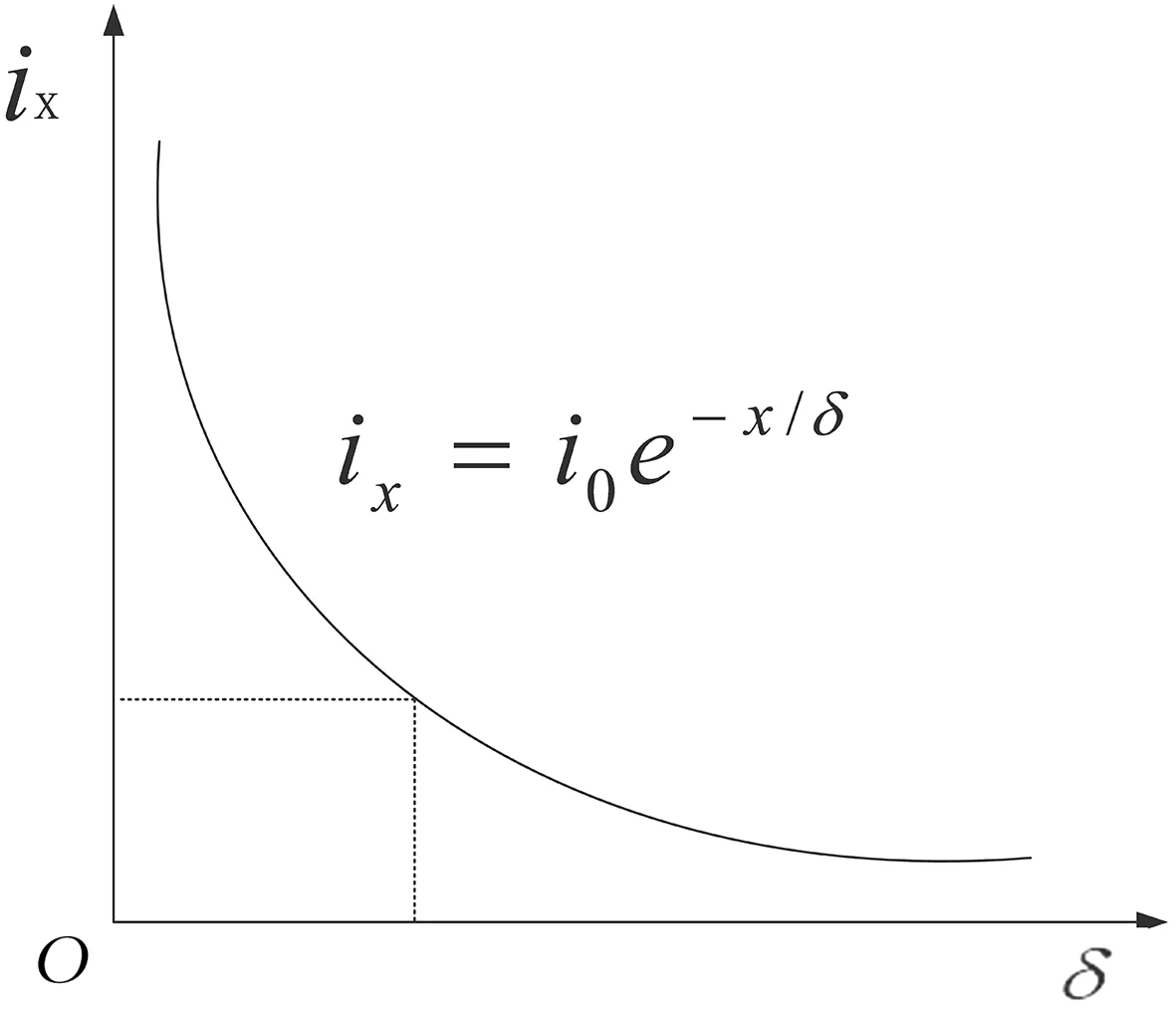
图1 电流密度随集肤层深度分布Fig.1 Distribution of current density with skin depth
现设金属导热层表面的电流密度为i0,金属导热层内部距离金属导热层表面x处的电流密度表示为
ix=i0e-x/δ.
(7)
式(7)中:δ表示集肤层深度,δ的表达式为
(8)
式(8)中:f表示电源变化频率,μ表示金属导热层在当前工作点下的相对磁导率,σ表示金属导热层电导率.
根据式(7)和(8)可以知道,在一定条件下,金属导热层的电导率、磁导率以及电源变化频率与金属导热层上的集肤层深度有关.改变电源变化频率,可以改变金属导热层的集肤层深度,从而会改变其温度分布.
1.2 涡流场及温度场有限元计算数学模型
对于线圈产生的涡流场,可以推出以矢量A为变量的表达式[8]:
(1/μrμ0)∇×∇×A=Js-σ(∂A/∂t).
(9)
式(9)中:μr为相对磁导率;μ0为真空中的磁导率;σ为电导率;Js为激励电流.对方程(9)进行求解,得到感应涡流:
J=-σ(∂A/∂t)=-jω,
(10)
电磁加热中,热源Qe是由涡流产生的焦耳热,表达式为
Qe=|J|2/σ,
(11)
用傅里叶热传导方程计算温度场,其表达式为
λ∇2T-cρ(∂T-∂t)=-Qe.
(12)
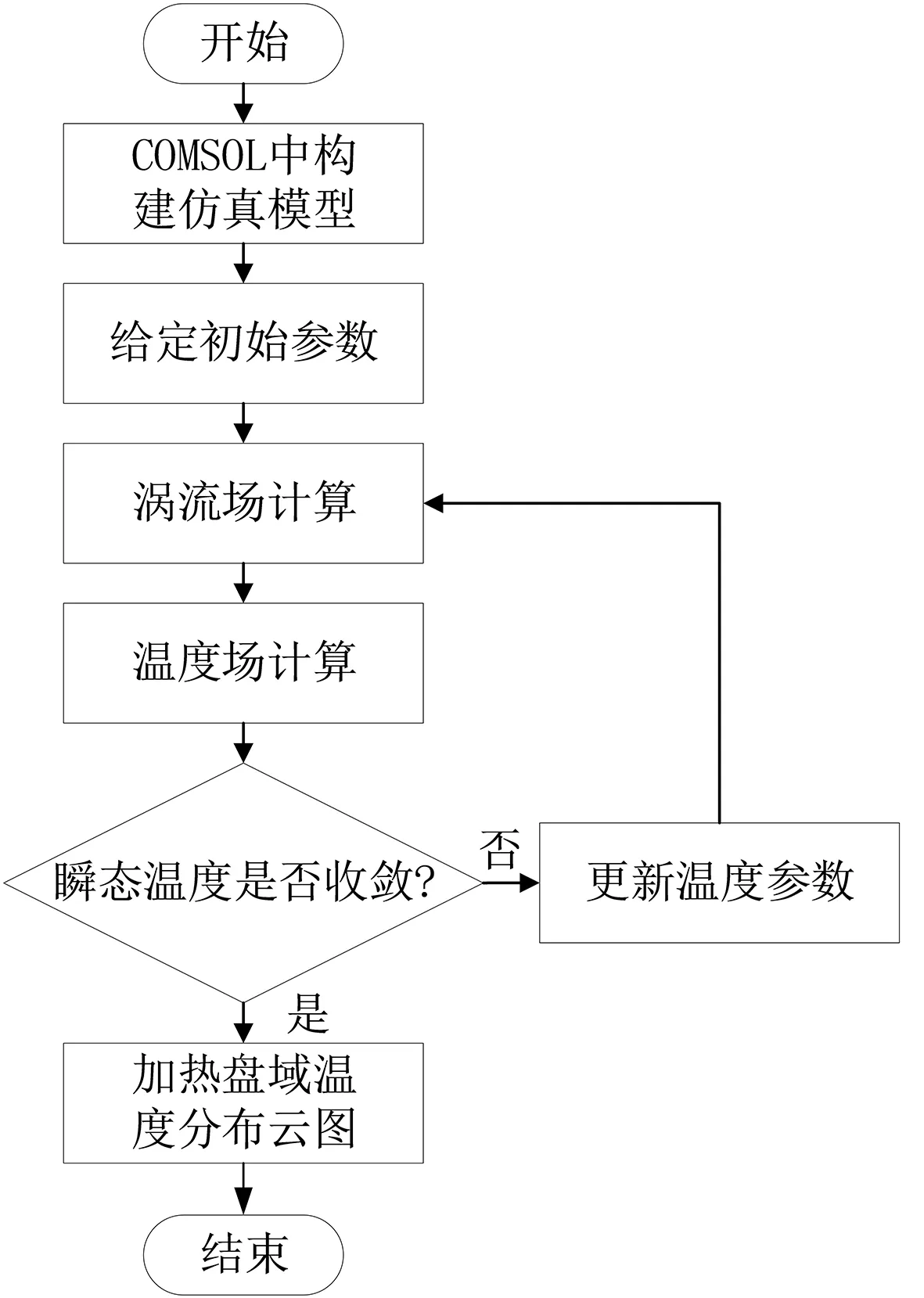
图2 富硒绿茶电磁理条耦合仿真流程Fig.2 Electromagnetic strip coupling simulation flow chart of selenium enriched green tea
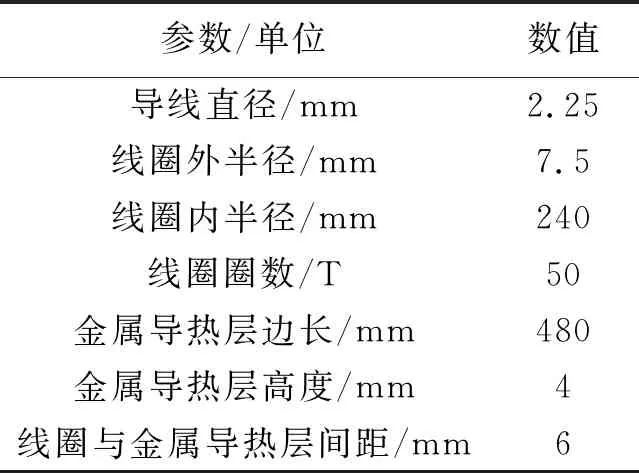
表1 电磁加热装置参数Tab.1 Parameters of electromagnetic heating device
式(12)中:λ为导热系数;c为比热容;ρ为物体的密度;T为温度.金属导热层表面因为对流引起的热量损耗由傅里叶边界条件确定,其表达式为
-λ(∂T/∂n)=h-(Ts-Tα).
(13)
式(13)中:h为对流热换系数;Ts为变化的表面温度;Ta为环境温度.联立式(10)~(13),可得出金属导热层表面任意时刻温度分布.
采用COMSOL Multiphysics 5.6软件进行仿真,电磁仿真过程为:建立三维模型,添加AC/DC模块中的电磁加热模块,进行建模,固体传热模块的设置、网格划分、对研究求解、后处理.对建立好的模型进行网格划分后,根据COMSOL中的进度,首先是对线圈产生的涡流场进行耦合计算,然后将涡流场的计算结果作为温度场的瞬态热分析载荷对金属导热层的温度进行计算,经过反复迭代收敛后,得出结果进行后处理.富硒绿茶电磁理条耦合仿真流程如图2所示.
2 仿真模型构建及有限元网格划分
2.1 模型构建
在COMSOL软件中建立富硒绿茶理条机电磁加热三维仿真模型,模型由金属导热层、线圈以及空气求解域3部分组成.金属导热层采用磁导率高且耐高温性的材料[9-10].线圈采用能够承受30 A电流、电阻率较低的4 mm2的铜制线.在线圈中通入频率为30 kHz、大小为10 A的交流电.由于线圈圈数过多,采用柱状体和长方体来替代.通过对单一线圈的仿真分析,选择均匀性最佳的一种结构,将其优化后,扩增为多线圈结构,应用于富硒绿茶理条机.电磁加热装置相关参数如表1所示.
在COMSOL软件中建立4种线圈结构的模型,如图3所示.
图3中的金属导热层与空气域的尺寸大小均相同,缠绕的线圈均为50 T.而对于图3(a)和(c),线圈的结构分别为圆形和方形,由于圈数过多,因此分别采用柱体和棱柱体来替代线圈.将50 T线圈均匀分布在其中,其线圈的间距均匀分布为2.6 mm.图3(b)和(d)的线圈结构相对复杂,为线圈间距不均匀分布,将其由内向外分为3段,分别为10 T线圈间距5 mm、10 T线圈间距4 mm、
30 T线圈间距1 mm.
2.2 网格划分
在仿真的温度升高过程中,金属导热层的物理性能会发生变化,因此为了使计算更加精确,需要经过反复迭代和合理划分网格[10].模型金属导热层网格划分如图4所示.
3 仿真结果与分析
3.1 4种线圈结构温度均匀性分析
在建立好的模型基础上,利用COMSOL软件对4种类型的线圈结构分别进行仿真.线圈中通入频率为30 kHz、大小为10 A的交变电流,并将电磁加热的时间设置为600 s.以每6 s为1个时间进程,进行迭代计算.得到的金属导热层温度分布云图,如图5所示.

(a) 圆形间距均匀型(b) 圆形间距不均匀型(c) 方形间距均匀型(d) 方形间距不均匀型图3 4种线圈结构的模型Fig.3 Four single coil structure models
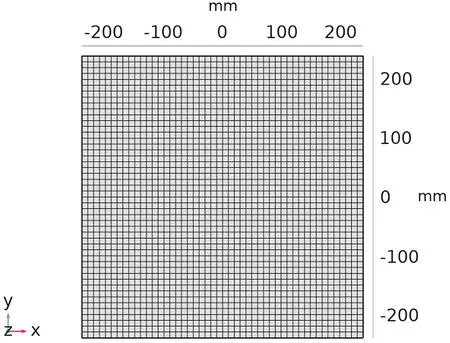
图4 金属导热层网格划分Fig.4 Grid division of metal thermal conductive layer
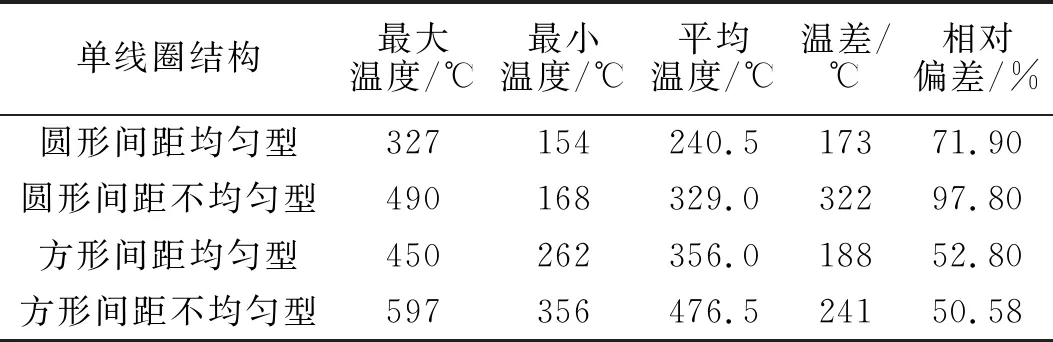
表2 4类金属导热层温度数据统计Tab.2 Temperature data statistics of four types of heating plates
在全部条件相同的情况下,线圈间距不同,分别对金属导热层的温度数据进行对比分析,A点为金属导热层温度最高点,B点为金属导热层温度最低点,有效加热区面积为整个金属导热层.
根据图5的仿真结果,可以得出:图5(a)~(c)在金属导热层4个角处均出现了最低温度点B.图5(a)和(b)产生的原因是,在四角处未有线圈分布;图5(c)的原因是其在边缘处面积较大,且线圈间距过大,磁感线相对较为稀疏.且图5(a)~(c)的温度分布,由外向内温度逐渐升高.对于图5(d),温度最高点A出现在边界,而几何中心处出现了温度最低点B.这是因为方形线圈的缠绕,边界段的线圈为30 T,间距为1 mm,线圈密集;因此几何中心段的线圈为10 T,间距是5 mm,线圈稀疏,因此几何中心处出现死区.

(a) 圆形间距均匀型 (b) 圆形间距不均匀型 (c) 方形间距均匀型 (d) 方型间距不均匀型图5 金属导热层仿真结果温度分布云图Fig.5 Cloud diagram of temperature distribution of metal thermal conductive layer simulation results
对其最高温度、最低温度、平均温度以及相对偏差进行统计,通过其温度差偏离平均温度的大小来反映金属导热层温度分布的均匀性,并对均匀性更好的方案进行优化.4类金属导热层温度数据统计如表2所示.
由表2可知:金属导热层最高温度出现在方形间距不均匀型的线圈模型中,平均温度最高的也为方形间距不均匀型的线圈模型.在相同时间内,方形间距不均匀型的线圈模型温度更高,且相对偏差率最低,为50.58%.则可得到线圈结构的优良性大小:方形间距不均匀型>方形间距均匀型>圆形间距均匀型>圆形间距不均匀型.因此,采用方形间距不均匀型的线圈模型应用于富硒绿茶电磁理条机加热装置,温度均匀性更好.
3.2 温度均匀性的影响因素
3.2.1 电流对金属导热层温度均匀性的影响 采用方形线圈间距不均匀型作为模型,由内到外3段线圈分别为30、20、20 T,共70 T.初始条件为:设定加热时间为600 s,在线圈中通入频率为30 kHz、大小为10 A的交流电,线圈与金属导热层之间的间距为6 mm.其他初始值不变,电流强度以0.5 A为增加量,从9 A增加至12 A.分别进行仿真,得到的仿真结果如图6所示.

(a) 9 A (b) 10 A (c) 11 A (d) 12 A图6 金属导热层表面温度分布云图Fig.6 Cloud diagram of surface temperature distribution of metal heat conducting layer
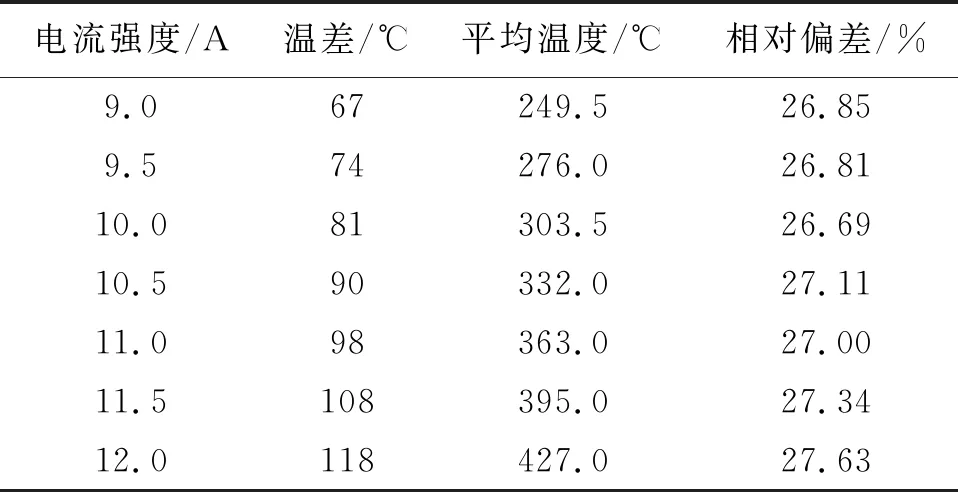
表3 电流强度增加对金属导热层均匀性的影响Tab.3 Effect data of increasing current intensity on the uniformity of metal thermal conductive layer
对金属导热层的最高、最低温度的温度差、平均温度、相对偏差的变化趋势进行分析,得到电流强度增加对金属导热层均匀性的影响数据如表3所示.
根据图6和表3可知:金属导热层表面最高和最低温度分布基本上相同.电流每增加0.5 A,温度每次增加约10 ℃,平均温度呈上升趋势.因此,在电磁加热过程中,电流强度越小,温度差越小,加热均匀性会越高.
3.2.2 频率对金属导热层温度均匀性的影响 线圈中的电流强度为10 A,加热时间600 s,线圈与金属导热层之间的间距6 mm保持不变,分别改变电流的频率20、30、40、50 kHz进行仿真,对其结果进行处理.计算在加热时间内,每个频率下的最高温度和最低温度的差值.并绘制出不同频率下温度差随时间变化情况,如图7所示.
由图7可知,从任意一条折线图来看,随着时间的增加,温度差在不断地增大.对照不同频率下的4条折线,在0~100 s时间段内,其温度差保持在同一水平,并呈现急剧增加的趋势;在300 s之后,温度差的增加趋势逐渐放缓.随着频率的增大,金属导热层表面的温度差减小,温度的均匀性越好.
3.2.3 线圈与金属导热层间距对金属导热层温度均匀性的影响 在电流强度、加热时间、电流频率、线圈间距等一定的情况下,只改变线圈与金属导热层间距,每次增加2 mm,分别为6、8、10、12、14 mm.并分别对其进行仿真,结果如图8所示.
由图8可得:随着线圈与金属导热层间距的增加,金属导热层的最高温度和最低温度都呈下降的趋势.在间距为6 mm时,温差为81.87 ℃,温度差最高;在间距为14 mm时的温差为70.74 ℃,温度差最小.因此,随着间距的增大,温度均匀性越好.
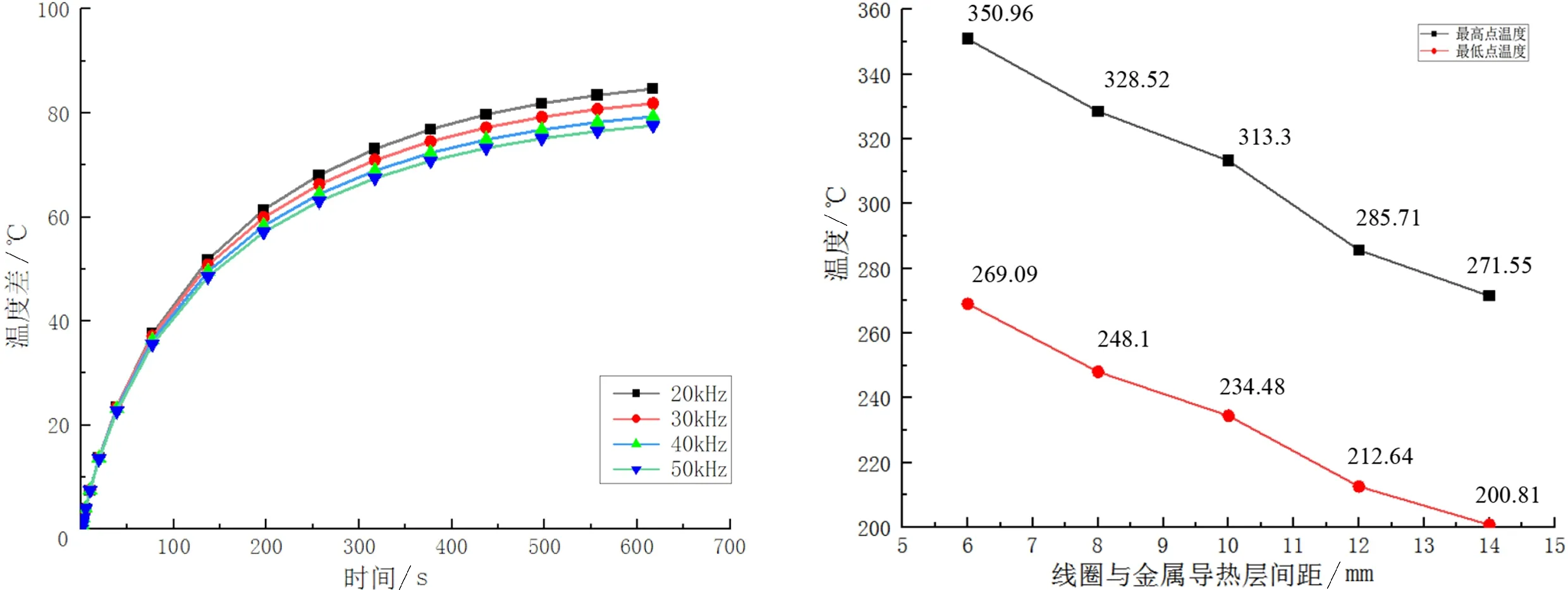
图7 不同频率下温度差随时间变化情况 图8 不同间距时的温度最高值和最低值
3.3 矩阵式多线圈结构仿真温度均匀性分析
现以11槽的富硒绿茶理条机为例,锅槽尺寸为64 cm×100 cm.对电磁加热模型在COMSOL软件中进行建模.采用方形线圈间距不均匀型模型,将其由内向外分为3段,每段线圈的圈数分别为40、30、20 T,而导线间的间距分别为1.25、0.75、1.75 mm.线圈均通入频率为30 kHz、大小为7.5 A的交流电.将建立的单一线圈模型进行2×3的阵列操作,得到与锅槽尺寸相同的电磁加热装置模型.
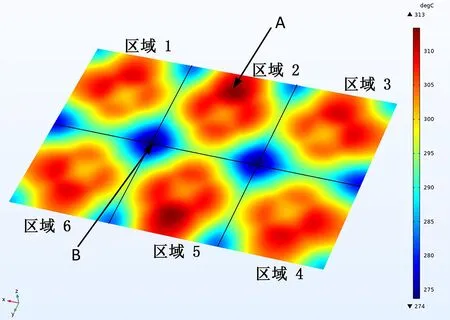
图9 矩阵式多线圈结构金属导热层温度分布云图Fig.9 Cloud diagram of temperature distribution of metal heat conducting layer with matrix multi coil structure
对构建好的模型进行仿真,设置加热时间为600 s,得到矩阵式多线圈金属导热层温度分布云图,如图9所示.
由图9可知,A点为温度最高点313 ℃,B点为温度最低点274 ℃,温差为39 ℃.温度均匀性与上述单一线圈结构相比,得到了明显地提升.因为采用矩阵式多线圈结构,线圈之间会相互影响,穿过区域2和5金属导热层的磁感线将会是区域1、3、4、6线圈所产生的叠加,因此温度会过高.在B点处产生温度较低的原因,是因为线圈间距相对稀疏,磁感线不如中部密集.矩阵式多线圈结构可以改善线圈中心的温度死区问题.
4 结论
在COMSOL中对富硒绿茶电磁理条线圈结构进行了优化设计,设计出4种单一结构的线圈:圆形线圈间距均匀型、圆形线圈间距不均匀型、方形线圈间距均匀型、方形线圈间距不均匀型,仿真后进行温度均匀性的对比分析,发现方形线圈间距不均匀型的温度均匀性更好.通过改变电流强度、频率、线圈和金属导热层间距,分析其对温度均匀性的影响.得到电流强度越小、频率越高、间距越大、温度均匀性越好的结论.最后,建立符合11槽富硒绿茶理条机尺寸的2×3矩阵式多线圈结构进行仿真分析,结果显示温度均匀性进一步提升.通过对线圈结构的优化设计以及温度均匀性分析,为富硒绿茶电磁理条机加热温度均匀性的改造提供了一定参考.

