限界约束下高铁升力翼气动布局研究

严日华，高 超，*，武 斌，刘 亚，丁绍成，倪章松，薛 明

(1.西北工业大学翼型叶栅空气动力学重点实验室,西安 710072；2.中国空气动力研究与发展中心,绵阳 621000)

0 引言

随着中国高铁技术的飞速发展，中国高铁已然成为了中国新的“外交名片”。为进一步推动中国高铁的发展，《交通强国建设纲要》中提出“合理统筹安排时速400公里级高速轮轨客运列车系统等技术储备研发”[1]。高速列车的再次提速虽然可进一步缩短高铁运输的时空距离，能为我国乃至世界提供一流的高品质、高安全、高科技含量的交通服务，但伴随着车速的提升，轮轨列车的车轮磨耗将加剧，这势必缩短车轮的镟修周期和使用寿命[2]。

近年来，一种带有升力翼的新型高速列车设计思路引起了人们的兴趣，这种新型高速列车[3]能有效提高列车气动升力，提升高速列车节能环保能力。日本东北大学[4-6]首先提出了气动悬浮列车概念模型，通过列车两侧的机翼在地面效应作用下产生较大的升力，从而提高运载经济效率。重庆理工大学赖晨光[7-9]等对单向翼布置的气动悬浮列车的地面效应进行了相关研究。但是鉴于现有高速铁路限界的约束，在高铁车厢两侧布放升力翼的方式升力翼的展长十分有限，提供升力较小，而在高铁车厢顶部布置串列翼的方式可以有效地提高升力翼的展长及数量。

目前国内外对于串列翼的研究大多数都是基于巡飞弹及无人机的布局设计，对串列翼布局气动特性的研究仅限于双翼，对多翼布局的研究十分有限。国外学者分析了两翼模型相对位置对升阻特性的影响[10-13]。国内也有学者通过数值仿真的手段对串列翼布局的气动特性随不同参数的变化进行了研究，并对相关布局参数进行了优化[14-18]。还有相关学者研究了串列地效翼布局水陆两栖飞机的气动特性[19]及排式充气机翼的气动布局[20]。对于高铁车厢上布置升力翼的方式，国内外相关研究表明，这种多翼布局存在较大的翼间干扰和严重的壁面效应。

本文基于现有高速列车限界约束，提出了一种高速列车多升力翼气动布局方式，分析了高速列车车厢对升力翼带来的壁面效应及多翼布局存在的翼间干扰影响。所提出的多翼布局方案利用气动升力等效减重，从而达到提高列车服役寿命，降低周期成本，减少列车运行能耗的目的，为气动升力高速协同列车的升力翼气动布局提供了设计参考。

1 升力翼设计参数及壁面效应影响

高铁车厢上可供布置升力翼的区域十分有限，在高速列车上布置升力翼会受到铁路限界的约束，如图1所示。高速列车的车厢宽度为3.4 m，本文约束机翼的展长为3 m。高铁车厢顶部距离桥隧界限的高度为2.4 m，为避免机翼与隧道洞壁产生壁面干扰，同时考虑接触网在极端天气下对机翼的干涉影响，所以需要对机翼布局高度进行约束。依据GB146《标准轨距铁路限界》“接触网距离地面高度为5.65 m，高铁车厢高度一般为3.7 m，车厢距离地面高度为0.35 m”的内容，可知车厢顶部距离接触网距离为1.6 m。为防止接触网与升力翼之间存在的干涉，本文将机翼距离高铁车厢顶部的高度限定在1.5 m。

图1标准轨距铁路界限示意图Fig.1 Schematic diagram of the boundary constraint of the standard gauge railway

图2 为高铁升力翼布局示意图。高铁车厢顶部布置的升力翼不仅受到车厢顶部产生的壁面干扰，还受到多翼布局下的翼间干扰及地面效应的影响。本文旨在分析高铁限界约束下的多翼布局，故在对多翼布局设计时主要考虑壁面干扰及各升力翼翼间的干扰，暂不考虑地面效应对车厢升力的影响。由于加入整车模型计算时间过长，而本文主要是研究壁面效应的影响，所以用平板模型来代替高铁车厢进行计算。

图2 高铁升力翼布局示意图Fig.2 Schematic diagram of the lift wing layout on a high-speed train

1.1 计算方法

忽略空气重力，三维非定常N-S方程在笛卡尔直角坐标系中的积分守恒形式[20]为：

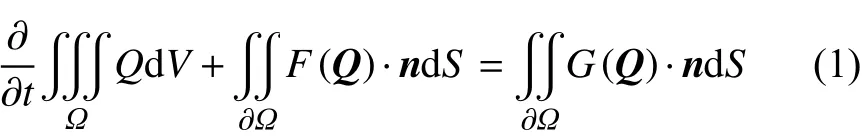
其中：Ω为控制体；∂Ω 为控制体单元的边界；Q为守恒变量；F(Q)为 无黏通量；G(Q)为黏性通量。

湍流模型选用S-A一方程模型，湍流黏性系数为：

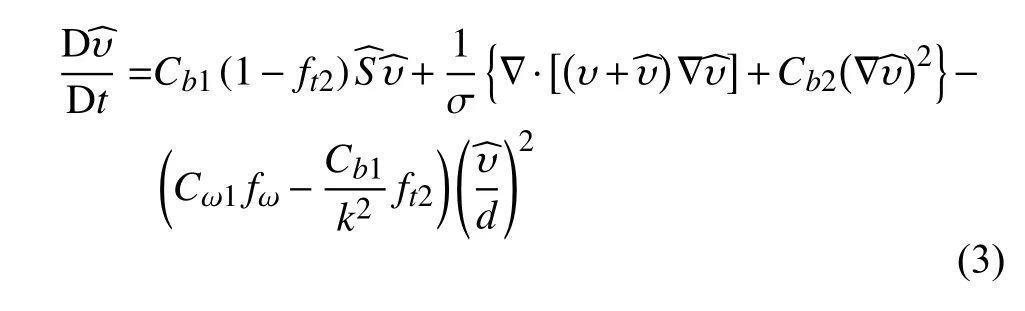
上述方程和控制方程的离散求解均采用中心格式的有限体积法。

在边界条件处理上，将远场定义为压力远场，速度为450 km/h；出口边界定义为压力出口，出口压力为101325 Pa；机翼及平板模型表面为无滑移物面边界。

1.2 算例验证

为了验证算法的准确性，本文对M6标模机翼在来流马赫数Ma = 0.8395、机翼迎角为3.06°状态下进行数值计算，将算得的M6机翼沿展向z/L=0.2、0.65、0.9剖面处的压力系数与实验结果[21]进行对比。结果如图3、图4、图5所示，可见本文计算值与实验值吻合较好，验证了算法的准确性。

图3 M6机翼沿展向z/L = 0.2剖面处的压力系数分布Fig.3 Chordwise pressure distribution at the spanwise location z/L = 0.2 of M 6 Wing

1.3 机翼参数

图4 M6机翼沿展向z/L = 0.65剖面处的压力系数分布Fig.4 Chordwise pressure distribution at the spanwise location z/L = 0.65 of M 6 Wing

图5 M 6机翼沿展向z/L = 0.9剖面处的压力系数分布Fig.5 Chordwisepressure distribution at the spanwiselocation z/L = 0.9 of M6 Wing

本文采用课题组自研的高升力翼型，该翼型相对厚度为20%，最大弯度位于弦长40%处，最大升力系数可达2.0，失速迎角为20°，在无人机的机翼设计中运用良好。由于在机翼设计中，平直翼产生升力的效率最高，故升力翼设计采用平直翼。机翼的展弦比选取直接影响机翼的升阻比。机翼展长一定时，展弦比减小，机翼特征面积增大，阻力增加；展弦比增大，机翼特征面积减小，升力降低。综合升阻比及特征面积，选取升力翼展弦比为6，升力翼展长为3 m，弦长为0.5 m，不同迎角下的机翼升力系数见表1和图6。

表1 不同迎角下升力翼升力系数Table 1 Lift coefficients of the lift wing at different anglesof attack

从表1和图6可知，升力翼的失速迎角为17°，此时升力翼的升力系数为1.655。考虑安装及升力翼迎角调节机构的误差，故将在升力翼的迎角为16°时分析多个升力翼的布局方案。

1.4 壁面效应对升力翼的影响

图6 机翼升力系数随迎角变化Fig.6 Lift coefficient variation with the angle of attack for the lift wing

图7 单翼壁面效应模型及网格划分图Fig.7 Computational model and grid for a single wing under wall effect

机翼的弦长为0.5 m，分别选取机翼距离壁面0.25、0.5、0.75、1 m四个不同高度进行数值仿真，此时机翼迎角为0°，分析壁面高度对壁面效应的影响。单翼壁面效应模型及网格划分如图7所示。迎角0°下单翼壁面效应计算结果如图8所示。机翼在距离壁面0.25 m高度上布置时，其升力受到明显影响，随着高度增加，壁面效应影响逐渐减弱，在高度达到0.50 m时，机翼升力恢复正常。继续增加机翼与平板模型之间的高度，机翼的升力系数几乎不变。可以得到：在壁面高度大于1倍弦长时，壁面效应对升力翼的影响将消失。

图8 0°迎角下升力翼升力随高度变化Fig.8 Lift force variation with the wall-normal height for the lift wing at 0°angle of attack

2 双翼布局方案研究

车厢上部布置单翼的布局方式升力十分有限，为增大车厢升力，需进行多翼布局，但此时翼间存在尾涡干扰。本节的主要目的是研究两片翼之间的距离及高度差等布局参数对其气动性能的影响。从上一节的数值仿真结果可以看出，当机翼离车厢高度超过1倍翼弦长时，车厢对机翼存在的壁面效应将消失，故在后续的计算中所有机翼离车厢的高度均超过1倍弦长。

2.1 同一高度，不同间距

为研究双翼间不同位置对整体气动性能的影响，本小节对双翼布局之不同翼间距进行分析。翼间距定义为前翼尾缘到后翼前缘的距离。由于在实际布放中翼间距会受到高铁车厢长度的约束，故在此节中仅对间距分别为1倍、2倍、3倍、6倍弦长四个工况进行计算，以分析翼间距对气动性能的影响规律。

本算例研究两片升力翼在同一高度（距离车厢上壁面均大于1倍弦长）、迎角同为0°时，不同翼间距的计算结果。计算结果列于表2。

表2 不同翼间距下升力翼升力系数Table 2 Lift coefficients for lift wingswith different wing spacing

如图9所示，前翼升力几乎不受翼间距影响，升力系数在0.39附近略有波动，这可能是由于数值计算过程中存在的误差导致。但是后翼升力系数变化明显：当翼间距为0.5 m（1倍弦长）时，后翼升力系数仅为前翼的46.5%；当翼间距为3.0 m（6倍弦长）时，后翼升力系数为前翼的61.25%。由计算结果可以得到：翼间距对双翼布局的气动性能影响较大，随着翼间距的增大，前翼对后翼升力系数的影响越小。

这是由于前翼翼梢附近的流体在绕翼梢卷起的同时，还要随来流向下游运动，此时会在翼梢形成尾旋涡，机翼的翼梢尾旋涡会在机翼周围产生小的向下的诱导速度，也就是下洗速度。前翼翼梢涡及尾流的影响，使得后翼的有效迎角降低，从而大大减小了后翼的升力。随着翼间距的增加，前翼产生的尾涡影响逐渐减弱，从而对后翼的升力影响逐渐减小。

图9 升力翼升力随翼间距变化Fig.9 Lift force variation with the wing spacing of lift wings

2.2 同一间距，不同高度

为研究双翼间不同高度差对整体气动性能的影响，本小节对双翼布局下不同翼间高度差进行分析。翼间高度差定义为前翼前缘点到后翼前缘点的高度差。双翼布局在高度方向上的高度差受到高压电缆和车厢之间距离的界限约束。现有资料显示，高铁车厢与高压电缆之间的高度差为1.5 m。基于1.4节的计算结果，为减少壁面效应的影响，机翼与车厢的高度差至少为0.5 m。所以本小节两片机翼之间的高度差最大不能超过1 m。

本小节研究两片升力翼在距离车厢顶部高度均大于1倍弦长、翼间距为3.0 m、迎角同为0°时，不同翼间高度差的计算结果。选取翼间高度差为0.2、0.5、0.8、1.0 m四个工况进行数值分析，数值计算结果如表3所示。

表3 不同高度差下升力翼升力系数Table 3 Lift coefficients of lift wings with different wall-normal height differences

从获得的数值计算结果可以看出：前翼升力几乎不受翼间高度差的影响，升力系数在0.389附近略有波动，这可能是数值计算过程中存在误差导致的。但是后翼升力系数变化明显：当翼间高度差为0.2 m时，后翼升力系数仅为前翼的66.2%；当翼间高度差为0.5 m时，后翼的升力系数为前翼的73.5%；当翼间高度差为0.8 m时，后翼的升力系数为前翼的80.4%；当翼间高度差为1.0 m时，后翼的升力系数为前翼的83.9%。由图10可知，翼间高度差对串列翼布局的气动性能影响较大，翼间高度差越大，前翼对后翼升力系数的影响越小，双翼布局的总体升力将增加。

图10 升力翼升力随翼间高度差变化Fig.10 Lift force variation with the wall-normal height difference for lift wings

这是由于下洗速度和来流速度叠加后会在机翼各个剖面处形成一个相对下偏的当地速度。作用在有限展长机翼上的下洗减小了每个翼型剖面所感受到的迎角。随着翼间高度差的增加，前翼下洗及尾缘涡对后翼的影响逐渐减弱，后翼的有效迎角逐渐增大，所以后翼的升力系数有所回升。

3 六翼布局方案研究

为进一步提升高铁车厢上升力翼提供的升力，本小节对六翼布局进行计算分析，迎着来流方向将各机翼 依 次 定 义 为Airfoil1、Airfoil2、Airfoil3、Airfoil4、Airfoil5、Airfoil6。分别对机翼距离高铁车厢顶部高度逐渐增加、高度逐渐降低以及同一高度三种不同布放方式下机翼产生的升力进行数值仿真。由于机翼数量较多，机翼后缘处需要网格加密，为减少计算量，本小节的三种布放方式均采用半模计算。

3.1 逐渐降低布局

升力翼的迎角均为16°，各升力翼距离车厢顶部的高度不同，第一片翼距离车厢顶部高度为1.5 m，机翼距离车厢顶部高度依次降低0.1 m，第六片翼距离车厢顶部高度为1.0 m。机翼在水平方向等间距均匀分布，翼间距为4.2 m。计算模型为半模。

计算得出：半模六片机翼总升力为38740.1 N，平均升力系数为0.9477，平均阻力系数为0.2008，总阻力为8206.1 N。由此可知，机翼总升力为77480.2 N，占单节车厢总重量（35 t）的22.59%。

表4表明，高度逐渐降低布局下，前四片翼的升力系数逐渐减弱，从第五片翼开始，升力系数逐渐增加。这是由于前翼上置、后翼下置的布放方式，后翼受到前翼尾缘涡的下洗作用更明显。前翼下表面存在的高压区域会使得后翼上表面的压力有所提升，此时后翼的上下表面压差减小，从而升力系数降低。结合图11可以看出从Airfoil1到Airfoil4，升力翼上表面低压区域逐渐减小，从Airfoil5开始升力翼上表面低压区域逐渐增大，上下表面压力差增大，从而导致升力系数有所回升。

表4 逐渐降低布局下升力翼升力系数Table 4 Lift coefficients of lift wings with gradually reduced wall-normal heights

图11 逐渐降低布局下对称面处六翼压力云图Fig.11 Pressure contours in the symmetry planesof six wings with gradually reduced wall-normal heights

3.2 同一高度布局

各升力翼的迎角均为16°，且距离车厢顶部高度相同，均为1.0 m。升力翼在水平方向等间距均匀分布，翼间距为4.2 m。计算模型为半模，网格数为980万。

计算得出：半模六片机翼总升力为45 720.1 N，平均升力系数为1.1184，平均阻力系数为0.21，总阻力为8 582.4 N。由此可知，机翼总升力91 440.2 N，占单节车厢重量的26.66%。

表5表明：同一高度布局下，前三片翼的升力系数逐渐减弱，从第四片翼开始，升力系数逐渐增加。结合图12可以看出，在该布局方式下，Airfoil1上表面的低压区域最大，由于前翼尾缘压力较高，前翼翼梢产生的尾旋涡会作用于后翼，后翼上表面压力有所提升，故Airfoil2上表面低压区域逐渐减小，Airfoil3受到Airfoil1和Airfoil2尾涡的共同作用，其上表面低压区域进一步减小，所以升力系数降低。从Airfoil4开始，后面的机翼上表面低压区域大小有所回升，从而升力系数逐渐增大。这是由于在同一高度布局下Airfoil1的尾涡强度最强，后翼产生的尾涡强度相比前翼有所降低，随着距离的增加尾涡强度逐渐衰减。Airfoil4与Airfoil1的水平距离超过15倍特征长度，Airfoil4所到Airfoil1尾涡的影响十分有限，因此Airfoil4所受到前三片升力翼的尾涡叠加强度不如Airfoil3所受到的前两片翼尾涡叠加强度大。并且从Airfoil4开始往后的机翼受到前面机翼的尾涡叠加强度逐渐减小，所以后三片升力翼的升力系数逐渐增大。

表5 同一高度布局下升力翼升力系数Table 5 Lift coefficients of lift wings with the same wall-normal height

3.3 逐渐升高布局

每片升力的迎角为16°，其距离车厢顶部的高度不同，第一片翼距离车厢顶部高度为1.0 m，机翼距离车厢顶部高度依次增加0.1 m，第六片翼距离车厢顶部高度为1.5 m。机翼在水平方向等间距均匀分布，翼间距为4.2 m。计算模型为半模。

计算得出：半模六片机翼总升力为45 402.81 N，平均升力系数为1.1083，平均阻力系数为0.214285，总阻力为8 758.9 N。由此可知，机翼总升力90 805.62 N，占单节车厢重量的26.47%。

图12 同一高度布局下对称面处六翼压力云图Fig.12 Pressure contours in the symmetry planes of six wings with thesame wall-normal height

表6表明，同一高度布局下，前三片翼的升力系数逐渐减弱，从第四片翼开始，升力系数逐渐增加。这是因为从Airfoil4开始，后面的升力翼受到前面升力翼叠加的涡强度逐渐减小，故升力翼上表面的低压区域逐渐增大，上下表面的压力差逐渐增大，所以升力系数逐渐增加。不同于同一高度布局，该布局下前三片翼的升力系数均有所提高，但后三片翼升力系数有所降低。这是因为随着翼高度差的增加，后翼受到的前翼下洗作用减弱，所以Airfoil2的升力系数相比同一高度布局有所提升，此时Airfoil2上下表面压力差增大，导致Airfoil2的尾缘涡强度增强。对比图13和图12可以明显看出：同一高度布局下Airfoil6上表面的低压区域明显比逐渐升高布局下Airfoil6上表面的低压区域大。从Airfoil4开始，高度的增加带来的升力提升量不足以抵消由前三片翼尾涡强度增强带来的升力降低量，故该布局下Airfoil4升力系数减小。

表6 逐渐升高布局下升力翼升力系数Table 6 Lift coefficient of lift wingswith gradually increased wall-normal heights

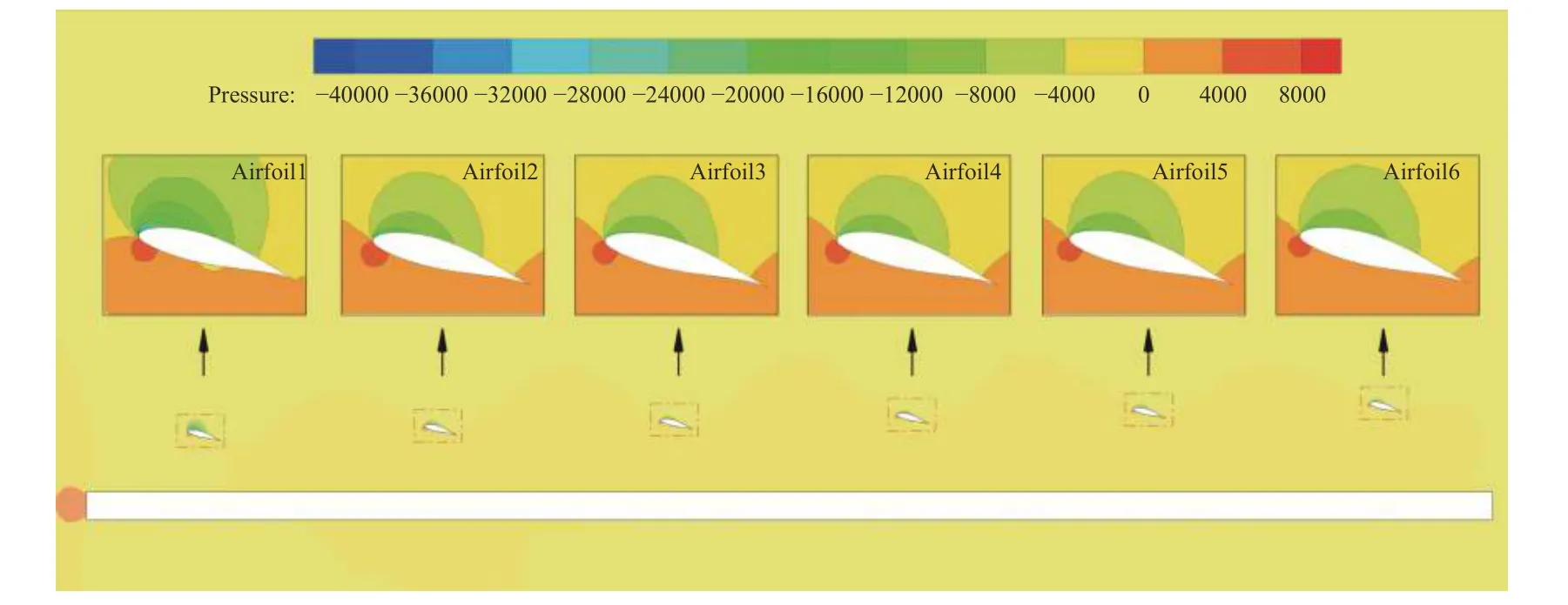
图13 逐渐升高布局下对称面处六翼压力云图Fig.13 Pressure contours in the symmetry planesof six wingswith gradually increased wall-normal heights

4 结论

本文基于现有高铁限界约束，探索了一种在高铁车厢上布置多片升力翼的气动升力协同高速列车概念模型，揭示了该布置方式下壁面效应及翼间干扰的影响规律，得到了三种六翼布局方式下高铁升力翼的气动性能参数，分析了各升力翼气动性能变化的原因，为气动升力协同高速列车的概念设计提供参考。具体结论如下：

1）壁面效应会严重影响升力翼的气动特性，随着升力翼距离车厢顶部高度逐渐增加，壁面效应逐渐减弱，在壁面高度大于1倍弦长时，壁面效应将消失。

2）多翼布局气动性能受两翼相对位置的影响较为敏感，前翼尾缘翼尖涡及下洗作用会减小后翼的有效迎角，随着翼间距及高度方向上距离的增加，翼间干扰将会减少，后翼的升力损失降低。

3）设计了三种六翼布局方式，三种布局方式的总阻力变化不大，总升力变化较大，同一高度布局方式总升力最大，可达到单节车身重量的26.66%。

本文工作侧重于现有高铁限界约束下气动升力协同高速列车概念模型的设计，重点分析了该设计下壁面效应及多翼间存在的翼间干扰的影响规律及原因，得到了一种能减少单节车厢26.66%重量的六片串列翼布局初步方案。暂未考虑地面效应对高铁升力翼的影响，在后续工作中将继续考虑整车模型及地面效应的影响，从而进一步优化多升力翼布局方式。