基于支持向量回归积和改进粒子群算法的特定区间盾构机作业参数选取

许哲东 侯公羽 杨 丽 黄小军

1.安徽工程大学建筑工程学院，芜湖，2410002.中国矿业大学(北京)力学与建筑工程学院，北京，100083

0 引言

在盾构机施工过程中，掘进参数对地表沉降有着非常重要的影响[1],如何选取最佳掘进参数是一个需要不断研究的课题。以地表沉降值为控制目标，掘进最优参数的选取包括非线性关系模型的建立和参数优化，非线性建模和优化方法的性能直接影响参数选取的准确性和可靠性。学者们采用了不同的方法来解决此类问题。基于对所选参数的分析，MOEINOSSADAT等[2]应用神经模糊推理系统建立所选参数与地面沉降值之间的非线性关系，通过不断更改选定的参数值，使地面沉降值最小化。李杰等[3]为在确保开挖面稳定的基础上提高实际施工现场盾构机掘进效率，进行了正交试验，同时，建立了掘进速度与掘进参数之间的数学模型，在MATLAB中对隧道参数进行了优化。曹曦等[4]分析了密封舱土压与掘进参数的关系，并采用最小二乘支持向量机建立了土压预测模型，同时基于粒子群算法实现了掘进参数的在线优化。羌培[5]针对超大直径的掘进参数匹配问题，采用BP神经网络模型建立了各盾构施工参数与隧道轴线上方地表沉降值之间的关系，再采用遗传算法实现了参数寻优。

学者们在一定程度上采用了不同的方法实现掘进参数匹配，但是，随着施工复杂度的提高，传统的参数选取方法难以实现，另外，随着工程项目越来越复杂，考虑的因素越来越多，对数据挖掘技术的性能要求也越来越高，在解决实际问题时，由于数据的不同特点，数据挖掘方法应用的性能也存在差异。因此，在目前盾构直径以及深度在逐渐增大的情况下[6]，如何提高特定区间掘进参数选取的准确性和可靠性是一个需要研究的问题。本课题从掘进参数选取中非线性建模和参数优化两个方面分别进行研究。

对于难以准确建立数学表达式的非线性关系建模，通常采用机器学习方法，如支持向量回归积(e-support vector regression，e-SVR)、随机森林(random forest，RF)和人工神经网络(artificial neural network，ANN)[7-9]，这些方法各有优缺点，在解决实际问题时，有必要根据具体问题分析选择最佳方法。为了更准确地实现特定区间掘进参数的选取，同时考虑地层参数、几何参数、掘进参数与地表沉降值之间的非线性关系，建立盾构机作业参数非线性关系模型。以实际盾构施工数据为基础，分析e-SVR、RF和ANN模型性能，得到建立盾构机作业参数非线性关系模型的最佳方法。

对于工程参数优化，智能算法是首选，它为各个行业提供了很多有效的解决方案。智能算法包括退火算法[10]、PSO算法[11]和遗传算法[12]等，其中，PSO算法广泛应用于许多领域[13-14]，但是，研究表明，标准PSO算法存在一些缺陷，很多学者对标准PSO算法进行了改进。SHI等[15]提出了一种线性递减的惯性权重调整等式，且给出了权重取值范围0.4～0.9。韩江洪等[16]为了降低算法出现“早熟”现象的概率，提出一种自适应调整惯性权重的PSO算法。封京梅等[17]为了求解不可微的NP难的绝对值方程问题，结合指数函数的曲线特征，提出了惯性权重指数递减的策略。根据学者们的研究得出惯性权重在迭代前期应取较大值，在迭代后期应为较小值的结论，然而，学者们并没有研究在迭代过程中，惯性权重下降速度对PSO算法性能的影响，因此，本文基于指数递减调整等式，采用指数函数中不同指数形式来控制迭代过程中惯性权重的下降速度，通过仿真实验，分析惯性权重降低速度对PSO算法性能的影响。根据实验结果，提出一种改进惯性权重降低速度粒子群优化(improved inertia weight decreasing speed particle swarm optimization，IIWDSPSO)算法。最后，基于e-SVR和改进粒子群算法实现对特定地层参数和几何参数区间的掘进参数优化选取。

1 PSO算法及其惯性权重降低速度仿真实验

PSO算法是模拟鸟群觅食的过程[18]。在迭代过程中，粒子速度和位置主要由两个最佳位置更新，包括粒子个体最佳位置和所有粒子中全局最佳位置。速度和位置由下式更新[19]：

vis(t+1)=ωvis(t)+c1r1(pis(t)-xis(t))+
c2r2(pgs(t)-xis(t))

(1)

xis(t+1)=xis(t)+vis(t+1)

(2)

式中，ω为惯性权重；r1、r2为位于(0,1)的随机值；c1、c2为加速因子；pis为第i个粒子在第s个方向上的个体最优位置；pgs为在第s个方向上的全局最优位置；xis为第i个粒子在第s个方向上的位置；t为迭代次数。

目前学者们所研究的惯性权重调整等式主要有线性递减调整等式：

(3)

随机调整等式：

ω=ωmin+(ωmax-ωmin)·rand(·)

(4)

非线性递减调整等式：

(5)

(6)

式中，ωmin为惯性权重最小值；ωmax为惯性权重最大值；rand(·)为随机函数；t为当前迭代次数；T为总迭代次数；d1、d2为常数。

根据指数递减函数曲线特点，可以发现这种函数曲线的变化趋势与迭代过程中惯性权重的变化是一致的。因此，采用指数函数中不同形式的指数来控制迭代过程中惯性权重的降低速度，可以看出它对算法性能的影响。

1.1 实验设置

根据指数递减函数式

(7)

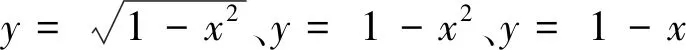
(8)

(9)

(10)

(11)

设置T为100，ωmin为0.4，ωmax为0.9，四种调整等式下惯性权重在迭代过程中的变化曲线如图1所示。

图1 惯性权重变化曲线

由图1可得，式(8)对应的惯性权重值在前期下降最慢，能够较长时间保持较大值，其次是式(9)和式(10)对应的惯性权重下降速度较慢，式(11)对应惯性权重值在早期阶段下降最快。保持其他条件相同，采用表1中10个经典测试函数研究惯性权重降低速度对PSO算法性能的影响。

表1 10个经典测试函数

表1中f1、f2、f3、f4、f5为单峰值函数，只有一个最优值，f6、f7、f8、f9,、f10为多峰值函数，存在局部最优值。四种不同惯性权重降低速度对应算法分别对每个函数独立运行20次。评价算法性能的指标有：20次运行的最小值、平均值、均方根误差(RMSE)和收敛目标完成率。实验参数设置如下：T=100，ωmin=0.4，ωmax=0.9，学习因子c1和c2为2，粒子种群规模为50。使用四种不同惯性权重降低速度的粒子群优化算法分别对10个函数进行优化,最终实验结果如图2～图5所示。

图2 20次独立运行的最小值

图3 20次独立运行的平均值

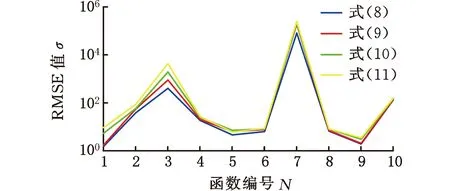
图4 20次独立运行的RMSE

图5 收敛目标完成率

1.2 实验结果分析

由图2可知，四种不同惯性权重降低速度的算法对单峰值和多峰值函数20次独立运行的最小值折线从低到高依次是式(8)、式(9)、式(10)和式(11)。与求解单峰值函数实验结果相比，四种不同惯性权重降低速度的算法求解多峰值函数得到的最小值折线比较接近，主要原因是多峰值函数中存在多个局部极值，因此获得全局最优值的难度更大。图3中，除了式(11)对应算法在f5函数中获得的寻优平均值低于式(10)对应算法寻优平均值外，在其他函数中，式(8)～式(11)对应算法获得的寻优平均值从小到大排序为：式(8)、式(9)、式(10)、式(11)。结果表明，在迭代初期，惯性权重下降速度越慢，算法优化单峰值和多峰值函数的准确性越高。

RMSE值是一个评价稳定性的指标。由图4可知，仅函数f5中式(11)对应算法寻优的RMSE值小于式(9)和式(10)对应算法寻优的RMSE值，但仍大于式(8)对应算法寻优的RMSE值。在其他函数中，RMSE值从小到大排列为：式(8)、式(9)、式(10)、式(11)。RMSE值表明在迭代初期惯性权重下降速度越慢，PSO算法在求解单峰值和多峰值函数中的稳定性越好。

根据图5中的收敛目标完成率条形图可得，除了f5，其他函数中收敛目标完成率值γ均满足γeq.(8)≥γeq.(9)≥γeq.(10)≥γeq.(11)，因此，从整体数值规律可以得出，在前期迭代中惯性权重下降速度越慢，收敛目标完成率越高。

由四种不同惯性权重降低速度对应算法在单峰值和多峰值函数中的性能分析可得，迭代前期惯性权重降低速度越慢，PSO算法精度、稳定性、收敛目标完成率越好。因此，基于实验结果，当采用指数递减函数式(7)的形式调整惯性权重时，指数x的最佳形式是圆心为0、半径为1的圆形公式，因此基于此提出了IIWDSPSO算法。

2 基于e-SVR和IIWDSPSO的特定区间盾构机作业参数选取模型

2.1 基于e-SVR的盾构机作业参数非线性关系建模

以地表沉降值作为控制目标，建立掘进参数、地层参数、几何参数与地表沉降值之间的非线性关系模型。掘进参数、地层参数与几何参数数值组成输入变量X，对应的地表沉降值作为输出变量yi。将训练样本映射到一个高维(l维)特征空间，采用下式线性回归：

f(X)=WTφ(X)+b

(12)

式中，W为l维权重向量；φ(X)为高维空间映射函数；b为偏置项。

基于ε不敏感损失函数，将回归问题转化求最优值问题：

(13)

约束条件为

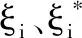
将以上优化形式进行转化：

(14)

对式(14)中W、b、ξ、ξ*求偏导，且令其为零，得

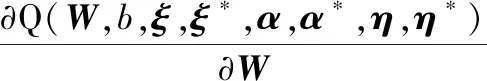
(15)

(16)

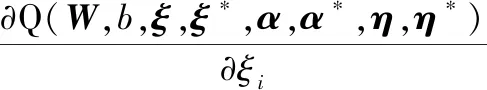
(17)

(18)

将式(15)～式(18)代入式(14)中，得其对偶问题：

(19)

约束条件为

基于实际盾构施工参数数据，求得最优解：

(20)

偏置项b通过卡罗需-库恩-塔克条件求解：

(21)

(22)

2.2 IIWDSPSO算法优化特定地层参数和几何参数区间的掘进参数

基于e-SVR构建的能够表达几何参数、地层参数、掘进参数与地表沉降值之间非线性关系的模型，以地表沉降值最小为优化目标，运用IIWDSPSO算法对特定几何参数和地层参数的区间掘进参数进行优化。

首先设置惯性权重的ωmin和ωmax，加速因子c1和c2，最大迭代次数T以及种群规模M。粒子空间位置向量由掘进参数、几何参数和地层参数构成，假设掘进参数、几何参数和地层参数共q个，则每个粒子空间位置Xs=(xs1,xs2,…,xsq)(s=1,2,…,M)。初始化算法迭代过程中掘进参数变化值作为粒子速度Vs=(vs1,vs2,…,vsq)(s=1,2,…,M)。注意，几何参数和地层参数是人为无法改变的量，因此，对应方向的速度需设为0。

根据最终训练得到的e-SVR模型计算IIWDSPSO算法中每一个粒子的适应度值，粒子j(j=1,2,…,M)的适应度ffit计算为

(23)

ffit(s)=1/f(Xs)

(24)

将初始化的粒子位置分别作为第一次迭代之前的每个粒子的个体极值Ps=(p1,ps2,…,psq)=(xs1,xs2,…,xsq)(s=1,2,…,M)，其中适应度值最大的粒子g的位置作为群体极值Pg=(pg1,pg2,…,pgq)=(xg1,xg2,…,xgq)。通过式(1)和式(2)更新迭代，惯性权重调整等式采用式(8)，循环迭代直到满足最大迭代次数结束。

3 基于实际盾构施工数据的模型验证

3.1 基于e-SVR构建的盾构作业参数非线性关系模型实际性能

结合实际工程盾构施工数据，对e-SVR建立的几何参数(深跨比H/D)，地层参数(水位d和重度W)，掘进参数(扭矩T0、总推力F、土舱压力ps、出渣量V、注浆量S和贯入度C)与地表沉降值h之间的非线性模型进行训练和测试，与此同时，和RF和ANN模型进行对比分析。施工数据来源于长株潭城际铁路工程项目[20]。所选参数和相应的样本数据折线图见图6～图8所示。

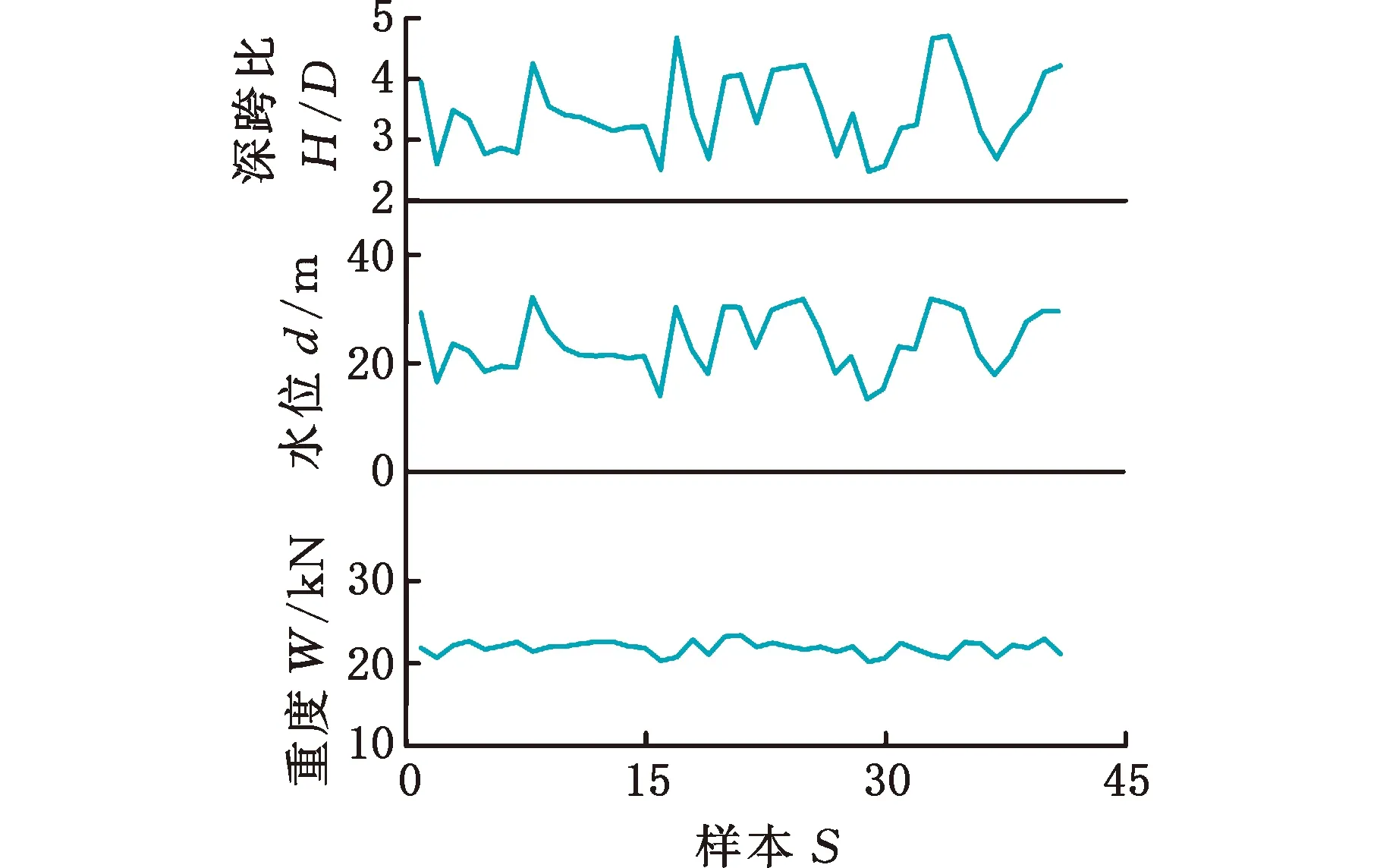
图6 41组几何参数值和地层条件参数值

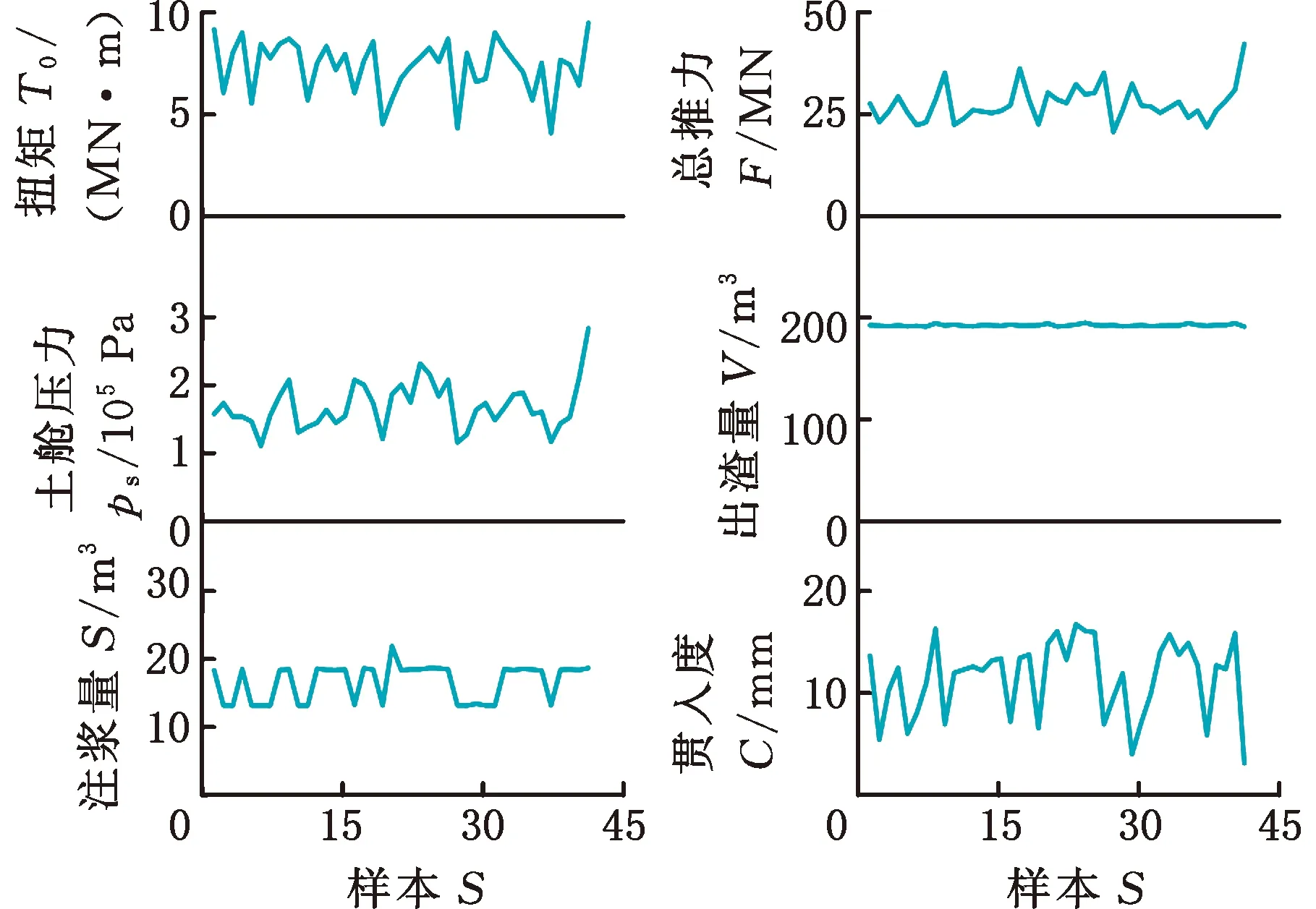
图7 41组掘进参数值

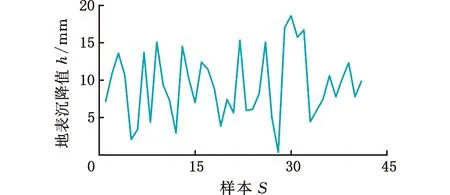
图8 41组地表沉降值

将图6和图7中前37组几何参数、地层参数和掘进参数作为训练输入样本，对应的图8中前37组地表沉降值作为训练输出样本,对e-SVR、RF和ANN模型进行训练。在实验中，通过反复训练得到各模型的最优结果。最终e-SVR模型中的参数值设置如下[21]：核函数类型为RBF，惩罚参数c=1.8，核函数的系数g=1.5，损失函数值为0.0001；RF模型主要参数设置为[22]：决策树最大深度为14，树的数目为50，分裂边界的个数为5；ANN模型参数值[23]：最大迭代次数为5000，学习效率为0.1。

最终得到的e-SVR、RF和ANN模型地表沉降预测值和实际值比较如图9所示。由图9可知，e-SVR模型中除了4个点不在直线上，其他点均拟合较好。RF模型各点基本都在直线上，而ANN模型对样本点的拟合较差。

(a)e-SVR模型

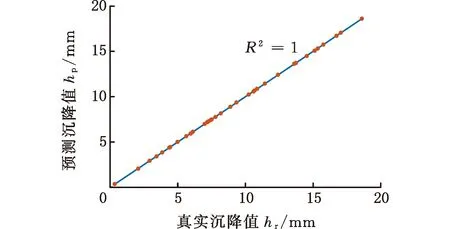
(b)RF模型

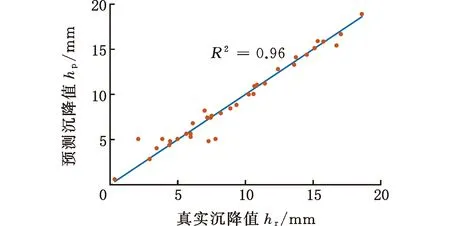
(c)ANN模型图9 模型拟合效果

基于训练得到的e-SVR、RF和ANN模型，使用测试集测试模型泛化能力，测试结果如表2所示。测试集中e-SVR、RF和ANN模型预测的相对误差平均值分别为0.06、0.24和0.07。所以，e-SVR模型得到的相对误差平均值最小。虽然RF模型对盾构作业参数样本有很好的拟合效果，但其测试结果相对误差平均值是最大的，表明了RF模型的泛化能力较差。因此，综合模型对盾构作业参数样本的拟合和泛化能力，可以得出e-SVR模型综合性能最好的结论。

表2 测试结果

3.2 IIWDSPSO算法优化特定地层参数和几何参数区间的掘进参数性能

基于3.1节获得的长株潭城际铁路工程数据建立的e-SVR模型，采用IIWDSPSO算法对几何参数和地层条件参数值如表3所示的隧道区段掘进参数进行优化，同时，与其他三种不同惯性权重降低速度的算法进行比较，最终优化得到的地表沉降值如表4所示。

表3 几何参数和地层条件参数值

表4 优化所得地表沉降值

由表4可得，IIWDSPSO算法获得的地表沉降值相对更小。基于IIWDSPSO算法得到的各掘进参数值分别为：刀盘扭矩值8406.99 kN·m，盾构推力值28 481.97 kN，土舱压力值1.85×105Pa，出渣量值194.32 m3，同步注浆量值17.96 m3，贯入度值16.27。最终优化得到的地表沉降值较为接近，但是根据本文方法的性能分析可知，基于e-SVR和IIWDSPSO模型获得的结果具有更高的可靠度。

在实际工程中，影响地表沉降的因素很多。目前，在模型中很难考虑所有因素，因此，在施工过程中，还需要根据模型得到的掘进参数值再进一步微调，模型的准确性和可靠性直接影响后期参数调整的效率。通过实验分析，本文提出的基于e-SVR和IIWDSPSO特定区间盾构机作业参数选取模型可以为实际工程中掘进参数的选取提供更准确和可靠的方法。

4 结论

为了提高特定区间盾构机作业参数选取的可靠性和准确性，研究了优化方法中PSO算法惯性权重降低速度对算法性能的影响，并提出了改进惯性权重降低速度粒子群优化(IIWDSPSO)算法。同时考虑掘进参数、地层参数、几何参数与地表沉降之间的非线性关系，基于实际盾构施工数据，将e-SVR与ANN、RF算法分别用于构建其关系模型并进行性能对比分析。最后基于e-SVR和IIWDSPSO算法实现特定几何参数和地层参数区间的掘进参数优化，得出主要结论如下：

(1)以地表沉降控制为目标，基于实际盾构施工数据，分析了e-SVR、RF和ANN模型的拟合和泛化能力，结果表明，e-SVR、RF模型对盾构作业参数样本有较好的拟合效果，但RF模型的泛化能力较差。综合考虑模型的拟合和泛化能力，e-SVR模型是盾构机作业参数建模的最佳选择。

(2)无论是单峰值函数还是多峰值函数，PSO算法的惯性权重在迭代初期降低速度越慢，PSO算法的优化能力越好。当采用指数递减函数(式(7))的形式调整惯性权重时，指数x的最佳形式是圆心为0、半径为1的圆形公式，即式(8)。

(3)基于实际工程中获得的掘进参数、地层参数、几何参数与地表沉降值之间的非线性关系e-SVR模型，采用IIWDSPSO算法和其他三种不同惯性权重降低速度的算法对特定地层参数和几何参数区间掘进参数进行优化，基于IIWDSPSO算法得到的最终地表沉降值相对更小。因此，所提出的基于e-SVR和IIWDSPSO算法的特定区间盾构机作业参数选取模型可以为实际工程中参数调整提供更准确可靠的参考。