自适应区间二型直觉模糊聚类算法研究
陈艺蕾,毕 杨
(1.西安航空学院 电子工程学院,西安 710077;2.西安邮电大学 通信与信息工程学院,西安 710121)
0 引言
图像分割是根据颜色、纹理等特征将图像分割为若干部分的操作,是图像预处理的重要组成部分[1-7],常见的图像分割方法有基于阈值的方法[8]、基于区域的方法[9]、基于边缘的方法[10]以及基于聚类的方法[11]。
模糊c-均值聚类算法(Fuzzy C-means Clustering Algorithm,FCM)[12-17]首次将模糊集的相关理论与聚算法相结合,将数据和样本类别之间的关系由“非此即彼”扩展为“亦此亦彼”,能够较为准确地描述数据的多重特征以及和样本类别之间的多种从属关系。但是,FCM中仅有一个模糊指数能够构造左右对称的模糊边界,因此对数据的要求较高,仅能够处理密度、大小相似的团状数据。为了解决这一问题,有学者在FCM的基础上提出区间二型模糊c-均值聚类算法(Interval Type-2 Fuzzy C-means Clustering Algorithm,IT2FCM)[18-19],通过两个模糊指数构造左右不对称的模糊边界,减少对处理数据的限制。但是,与FCM相同,IT2FCM通过聚类中心和隶属度交替迭代实现目标函数最小,这种方式使得聚类效果依赖于初始聚类中心的选择,如何确定合适的初始聚类中心是研究的一个热点问题。
本文提出一种全新的自适应区间二型直觉模糊聚类算法(Adaptive Interval Type-2 Intuitionistic Fuzzy Clustering Algorithm,AIT2IFCM),通过提取图像中的直方图信息进行平滑处理并且设计波峰与聚类中心的对应规则确定合适的初始聚类中心;另外,为了更好地处理图像中的细节信息,提出一种融合直觉模糊信息的目标函数,通过类内类间两方面的信息共同评判聚类效果;最后,将本文算法应用于彩色图像分割中更加直观具体的验证算法性能。
1 区间二型模糊聚类算法

(1)

(2)
IT2FCM通过两个模糊指数将隶属度扩展为一个区间,通过Karnik-Mendel算法[20]将二型模糊集进行降型进而计算得到与之相对的区间聚类中心[vL,vR],计算方法如下所示:
(3)
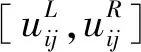
(4)
其中,M表示像素的维度。最后取区间的中间值得到确定隶属度uij和隶属中心vj。当‖vj-vj-1‖≤ε时,则算法停止迭代,最终利用最大值取模糊法得到聚类结果。计算公式如下所示:
当uij>uik,k=1,2,…,c,j≠k,则xi属于第j个聚类中心。
2 自适应区间二型直觉模糊聚类算法
2.1 确定直方图引导的初始聚类中心
图像的统计直方图蕴含丰富的信息,可以直观的反映出图像各像素的数量及其占比。长久以来,直方图作为一种显著的特征信息被广泛应用。在本文中,将图像的直方图信息应用于IT2FCM的初始聚类中心确认中,结合待处理数据为彩色图像的特点,对图像R、G、B三个维度的特征分别进行直方图统计。以伯克利图库中#3 096为例,图像及其统计直方图拟合曲线如图1所示。图1(a)为图像;图1(b)为R维度的直方图拟合曲线;图1(c)为G维度的直方图拟合曲线;图1(d)为B维度的直方图拟合曲线;图1(e)为R维度的平滑直方图曲线;图1(f)为G维度的平滑直方图曲线;图1(g)为B维度的平滑直方图曲线。如图1(b)、图1(c)、图1(d)所示在图中可以直观看到波峰和波谷,也可以看到原直方图中存在非常多的细小毛刺,这些毛刺对于波峰的选取有较大的干扰,因此,本文利用高斯滤波函数对直方图进行平滑处理,从而消除毛刺对选峰的干扰。具体方式如下所示:
F(x)=H(x)×G(x)
(5)
其中:F(x)表示平滑滤波完成后统计直方图的拟合曲线;H(x)是将原图统计直方图拟合曲线进行傅里叶变换得到的频域信息;G(x)则表示频域高斯滤波函数[21],计算方式如下所示:
(6)
其中:x表示像素值;σ表示图像像素的标准差。如图1(e)、图1(f)、图1(g)所示,经过平滑的直方图拟合曲线能够在保持数据特征的基础上去除毛刺,避免对选峰产生影响。

图1 图像及其统计直方图拟合曲线
在实际应用中,直方图中存在的波峰数量f往往与理想的聚类数目c不匹配,因此,设计了波峰和聚类中心的对应规则,具体如下所示:
(1)若f≥c,则选择峰值最大的c个波峰所对应的像素值作为聚类中心;
(2)若f 传统的目标函数仅仅考虑了数据与聚类中心之间的距离和从属关系,未考虑各个类别之间的关系。为了更加全面的评价聚类的效果,本文提出一个新颖的融合直觉模糊信息的目标函数fAPI,不仅同时考虑到类内紧致性和类间分离性两方面的内容,还通过加入直觉模糊信息更好地处理细节信息,具体计算方式如下所示: (7) 其中:c表示聚类数目;E1表示整个数据的紧凑程度;Ec表示区间二型模糊聚类的类内,其计算方式如下所示: (8) (9) 将直觉模糊信息引入模糊聚类的评价中时,xi扩展为隶属度t(xi)、非隶属度r(xi)和犹豫度π(xi)三个分量。r(xi)通过Yager′s生成函数[22]计算得到: r(xi)=(1-t(xi)α)1/α,0<α<∞ (10) 其中,α取经验值0.85,π(xi)通过三个关系计算得到: π(xi)=1-t(xi)-r(xi) (11) 直觉模糊距离dIFS(xi-vj)的计算方式为: dIFS(xi-vj)=sqrt((t(xi)-t(vj))2 (12) 表示类间分离的函数Dmax通过下述方式计算得到: (13) 为了进一步验证AIT2IFCM的有效性,本文将FCM、直觉模糊聚类算法和区间二型模糊聚类算法作为对比算法,其中三种对比算法均为随机初始聚类中心。对于模糊指数,FCM和IFCM为一个模糊指数,取经验值m=2,IT2FCM和AIT2IFCM中两个模糊指数分别取m1=2,m2=2.5。将本文算法和对比算法分别用于伯克利图像的彩色分割中,利用分割准确率评价各算法的聚类分割效果,各算法准确率对比如表1所示。 表1 各算法准确率对比 为了更加直观的展示分割的结果,分别将#135 069、#147 091和#238 011的分割展示在图2至图4中。 在图2中,两个大雁中间白色部分为分割的难点,可以看到,其他对比算法均有大面积错分,只有本文算法能够准确地将图像分为三个部分。对于#147 091,FCM、IFCM和IT2FCM虽然能够准确分割出松树,但右上角的错分比较严重,本文算法不仅能够准确的分割出松树,右上角的错分情况有明显的减少。综上可得出结论,加入了直觉模糊信息的目标函数能够有效的处理图像中的细节信息。在#238 011中,月亮所占像素比例较小,初始聚类中心不当时,月亮的信息不能准确的提取出来,利用直方图信息确定聚类中心能够准确地确定出三个初始聚类中心并得到良好的分割结果。 图2 #135 069 (a)原图;(b)标准图;(c)FCM分割图;(d)IFCM分割图;(e)IT2FCM分割图;(f)AIT2IFCM分割图 图3 #147 091 (a)原图;(b)标准图;(c)FCM分割图;(d)IFCM分割图;(e)IT2FCM分割图;(f)AIT2IFCM分割图 图4 #238 011 (a)原图;(b)标准图;(c)FCM分割图;(d)IFCM分割图;(e)IT2FCM分割图;(f)AIT2IFCM分割图 针对区间二型模糊聚类算法对聚类中心敏感的问题,本文提出了一种全新的自适应区间二型直觉模糊聚类算法(AIT2IFCM)。首先提取了图像中的直方图信息进行平滑处理并且设计了波峰与聚类中心的对应规则确定合适的初始聚类中心;另外,提出一种融合直觉模糊信息的目标函数,通过类内类间两方面的信息共同评判聚类效果,从而更好地处理图像中心的信息;将本文算法应用于伯克利图像分割中,结果表示本文算法不仅能够准确地确定合适的初始聚类中心并且能够有效地处理图像中心的细节信息。2.2 构造融合直觉模糊信息的目标函数
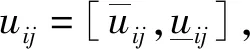
+(r(xi)-r(vj))2+(π(xi)-π(vj))2)3 实验结果及分析




4 结论

