漂浮式光伏网格对海上天气突变的感知方法

姜淏予， 王沛伦， 葛泉波， 徐今强， 罗 朋， 姚 刚

(1. 广东海洋大学 电子与信息工程学院，广东 湛江 524088； 2. 上海海事大学 物流工程学院，上海 200135； 3. 南京信息工程大学 自动化学院，南京 210044)

近年来，中国连续提出海洋发展战略，在广东省西部地区主要表现在海洋农业向远海区域的开发利用.但海上突发气象变化往往对养殖业造成不利影响，且由于远海监测条件有限，海上气象环境更为复杂多变，使得有关系统对局部极端天气的预测能力不足.如果不能提前估计海上天气变化并做出保护反应，有可能会对产量造成频繁冲击甚至绝收[1].因此需要依托海上相关工程，在边缘层实现海上气象的自动化智能感知，进而依托无人系统开展保护与管控.对无人系统尤其是远海条件无人系统供给能量，主要依托海上可再生能源，包括风能、太阳能、波浪能、潮汐能等[2].漂浮式光伏系统作为近年来高速发展的一种可再生能源发电技术，具有技术相对成熟、施工难度较低的优势.

传统漂浮式光伏发电系统最早应用于美国、日本等发达国家[3]，主要用于缓解光伏建造工程占地面积大导致的成本过高问题.作为最早的研究国家之一，日本在漂浮式光伏系统应用方面保持着世界领先地位，先后在Hyogo、Higashira、Yamakura、Aichi、Okinawa、Umenoki、Furugori等地建设有示范工程，发电功率最大达到了13.4 MW[4].我国于2015年在湖北枣阳建成首个水面漂浮式光伏发电站试验项目，装机200 kW[5]，随后装机容量不断扩大，直到近些年多个项目达到100 MW的规模并成功并网.然而，当前漂浮式光伏系统在海上的应用较少，原因在于以上漂浮式光伏系统主要以大型发电建设为主要目标.考虑到海底电缆的施工技术要求以及海洋水下环境的复杂性，在地上优质水面资源没有完全开发之前，漂浮式光伏的商业应用不会优先在海上开展.

采用漂浮式光伏作为能源系统对海上边缘侧的无人系统供电避免了通过海底电缆传输回陆地的主要矛盾，因此，结合近年来已有研究[6]，海洋漂浮式光伏发电作为海上无人系统电源是可行的.由于光伏出力极易受到辐照度、环境温度、风速等因素的干扰，所以其非连续、随机的特点吸引了大量的相关研究.文献[7]通过将气象条件相似的天气进行分类后选择相似日，对每个相似日的光伏出力进行建模并预测.文献[8]在选择相似日后探讨建模过程并由神经网络进行构建；文献[9]在选择相似日后，进一步对由光伏电站空间分布造成的区域气象变化进行分类，以期取得更好的建模条件.文献[10]进一步指明通过聚类与数据挖掘能够预测某些系统，即人工智能方法对于功率预测具有实践意义.目前，多数研究都在采用人工智能方法的基础上结合数据挖掘等技术从光伏功率出力角度进行建模，这种统计学习方法虽然避开了复杂的物理机理研究，但需要较多历史数据，在光伏电站预测的效果上仍存在泛化性能较差等问题.但是，这种由于气象强相关性而导致的光伏出力预测性的难点却可以用来感知海上气象环境的高度突发性与不确定性，且有助于利用相关性来融合估计目标光伏出力，从而避免采用端到端过度复杂的模型以及传统方法过拟合的风险.本文主要讨论该漂浮式光伏系统，在针对海上牧场网格化建设后，通过对其出力状态的分析，判断该系统是否可以感知气象条件的突变.

1 问题描述

1.1 模型描述

采用固定式浮筒安装方式，浮筒之间采用螺栓刚性连接，并在外围布置减震器.部分采用活动铰接装置，将浮体、连接杆和陆地等固定物串联在一起，或用缆绳锚固于岸上，部分水域采用打钢桩、预制桩固定.以上安装方式使得海上光伏的U-I机理模型从理论上更接近陆地的理想状态，主要因为海上环境内的灰尘更少，使得组件不会因为灰尘附着而减少功率输出，且水对光伏阵列的冷却作用可以提高输出电量[11].根据光生伏特效应，通过光伏电池将光能转化为太阳能，其U-I特性[12]为

(1)

式中：I为太阳能电池的输出电流；Iph为光伏电池的光生电流；Id为反向饱和电流；q为电荷常数；U为光伏电池电压；Rs为内部串联损耗；A为二极管品质因子；K为玻尔兹曼常数；T为光伏电池温度；Rsh为光伏电池等效并联电阻.Iph与Id是随环境变化的量，需要根据光照强度和温度确定，其计算式为

(2)

(3)

式中：Isco为标准日照和标准温度时的短路电流；ht为温度系数；Tref为标准温度，数值为25 ℃;S为当前辐照强度；额定太阳辐射强度Sref=1 000 W/m2；系数a1=1.336×104,b1=225.最后考虑光伏电池浮体在海面受到海浪影响的摆动作用[13]，根据六自由度的水动力分析，在规则波影响下可认为海浪中浮体的角度摆动为简谐运动.对于轻浪与中浪的海况条件，根据线性波理论可知浮体质点的运动近似于圆周运动：

(4)

(5)

式中：α为海浪中浮体的角度；αmax为浮体摆动的最大角度；γ为浮体摆动周期；α0为初始相位；XA、YA为在一个规则海浪作用下质点在二维平面两个基方向的运动轨迹；R为波高的一半；θ为近似圆周运动的角度；υ为波速；τ为时间.

总体而言，在一个摆动周期内海上光伏电池接收辐射能约为陆地最佳条件的87%，但这主要针对小规模的漂浮体、4级以上海况而言.对于水上漂浮式光伏面积较大、海况等级较低的情况，可以认为海上光伏的实际出力与陆地接近.根据物理法对光伏出力的预测模型，光伏阵列由多个光伏电池串并联而成，由于客观上存在的串联限制电流与并联限制电压的作用，N块光伏组件的组合的光伏出力并不是单个光伏组件的N倍.描述光伏阵列U-I特性的5参数模型[14]如下：

(6)

式中:Vpv、Ipv分别为光伏阵列输出电压、电流；Npp为光伏组件串的并联数；光电流IL、二极管反向电流IO、理想因子ε、串联电阻R1和并联电阻R2为模型的5个参数；Ns为单个光伏组件中光伏电池的串联数；Nss为光伏组件串的串联数.只要已知未来时刻的5个参数，即可通过模型进行预测.物理法具有不需要大量历史数据、结构清晰等特点，缺点在于实时的气象条件数据难以获得，电站的精确建模困难.对海上问题而言，由于光伏电池表面的辐射能由直射辐射、散射辐射和反射辐射3部分组成，所以式(1)中的Iph与式(6)中的IL作为一个电流源实际上是与海面反射率与大气透明系数有关的函数，影响作用如下：

(7)

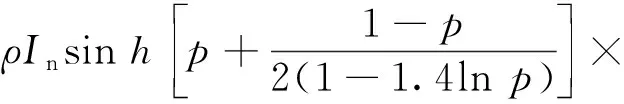
(8)

式中：Is、Ig分别为散射辐射与反射辐射；In为地表总辐射能；h为太阳高度角；p为大气透明系数；ω为光伏电池安装夹角；ρ为海面反射率.

可以看到，如果直接采用物理模型方法，则有些参数不易被实时精确获取，因此考虑引入数据统计法.统计法使用的模型方式较多，通常是对不同天气情况下的数据分类后寻找规律，构建模型.常用的方法有灰度模型、时间序列分析中的差分整合移动平均自回归(ARIMA)模型等，包括人工智能算法先对数据进行数据聚类分析改进的神经网络构建模型[15]等方式.统计法的优点在于从历史数据中找寻规律，从而无需获得实时的气象数据.本质上，统计法的依据是气象条件的相似性以及气象情况在时空间上的连续性.这些变化会客观地反映在数据之中，寻找出数据规律即可创建模型.以上两种方法的结合如图1所示，其重点放在气象条件的分析处理上，通常使用相关性分析、主元分析法等方法筛选出对光伏出力数据影响最大的因素，将这些气象因素作为神经网络等其他人工智能方法的输入[16-17]，训练模型后进行预测，结合法的目的为选定对光伏功率出力影响最大的气象因素，通过建模手段预测得出未来的气象因素状况，代入至光伏阵列的物理模型中得到预测结果，该预测结果包括对天气的预警信息.

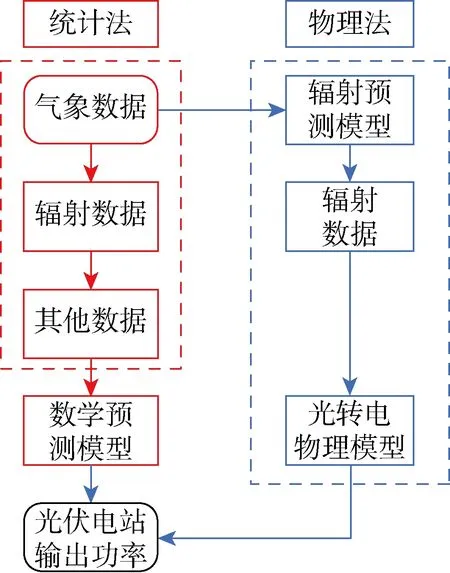
图1 物理法与统计法流程Fig.1 Process of physical method and statistical method

1.2 研究动机

图2所示为光伏发电流程与影响因素，由于气象条件与光伏电站的输入高度相关，所以各种预测方法要直接或间接考虑气象条件的影响[18].例如传统物理方法基于太阳辐照传递方程、光伏组件运行方程等物理方程进行预测，需要光伏电站详细的地理信息以及气象和太阳辐照数据，对于分布式光伏电站建模过程复杂，且难以模拟一些极端异常天气情况和环境及光伏组件参数随时间发生的缓慢变化，模型抗干扰能力较差，鲁棒性不强，这种特点在海上漂浮式光伏网格系统中尤其明显，可以视为分布式光伏问题.采用纯粹的统计学方法，基于预测模型输入、输出因素之间的统计规律进行预测，目前缺少准确的甚至可迁移的历史运行数据.因此在实际应用中大概率会出现过拟合问题，使得建立的模型复杂且不具有通用性.

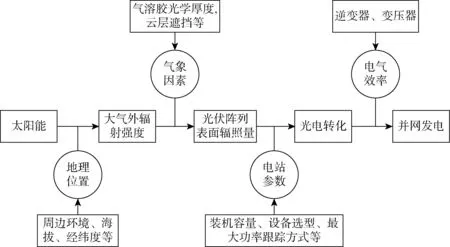
图2 光伏发电流程与影响因素Fig.2 Photovoltaic power generation process and influencing factors

在结合法思想基础上，针对上述光伏出力预测思路中存在的问题，对海上光伏系统有关问题提出以下改进思路：① 基于云层移动带来的客观变化特点，进一步分析选取相似电站的影响因素，并提出一种改进密度聚类方法以精确选择相似电站；② 由光伏功率能量来源有限的特点引入物理法中的光照辐射强度模型与光伏阵列模型以约束预测值；③ 设计一种简单的方法给出光伏功率预测范围，并采用长短时神经网络拟合各环节中忽略的因素造成的误差，修正后给出预测值，进而等效于给出气象问题中云层移动变化的追踪预警结果.

2 相似电站的因素分析及其选取

相似电站[19]即功率曲线相似的电站，常常用以补全异常数据或扩大数据集.对相似电站的选取，通常使用斯皮尔曼相关系数或时序相关性分析.从海上气象感知问题出发，主要分析相似电站过程的时空影响因素.

2.1 电站的固有影响因素

由1.1节讨论的光伏阵列模型相对复杂，工程上一般从能量的角度给出模型.光伏阵列输出功率计算公式[20]如下：

(9)

式中：PG为装机容量；S0为辐照强度；T0为环境温度；0.036[1-(T0-25)]为温度T0造成的影响项.辐射照度为光伏功率的能量来源，其对光伏功率的影响不言而喻.电站的装机容量为系统建立时即可确定的参数，决定了电站能够接受能量的大小.其他因素如积灰、倾角、温度等造成的影响相较于辐射照度与装机容量影响不大.在预测工作中，装机容量数据易于获得，而经云层遮挡的光伏阵列表面辐射照度数据难以获得，对预测工作造成极大困扰，因此统计法期望寻找云层移动反映在数据上的规律并建模.但光伏发电数据波动的来源有两部分：辐射照度的时间变化和云层遮挡造成照度变化.这使得使用数据训练建模的过程变得复杂，由于晴朗天气下的光照强度模型简单，将其引入至统计法的流程中以更好地探寻由云层遮挡带来的变化.

2.2 电站间距离的影响及其分析

在相似电站的选取过程中，通常会显现距离相近的电站出力结果相似的现象.如图3所示，图中数字1～7为电站编号，7个电站间距离最远的两个电站间距为1.5 km，装机容量皆为15 kW.7个电站在同一天的功率曲线如图4所示，图中k为时刻.

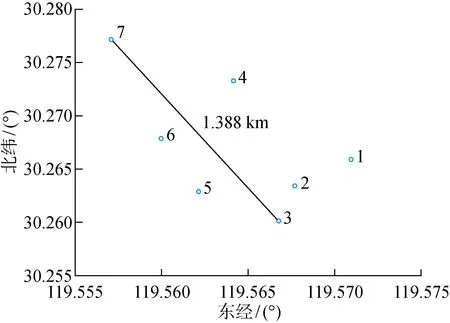
图3 电站分布位置Fig.3 Distribution location of power stations

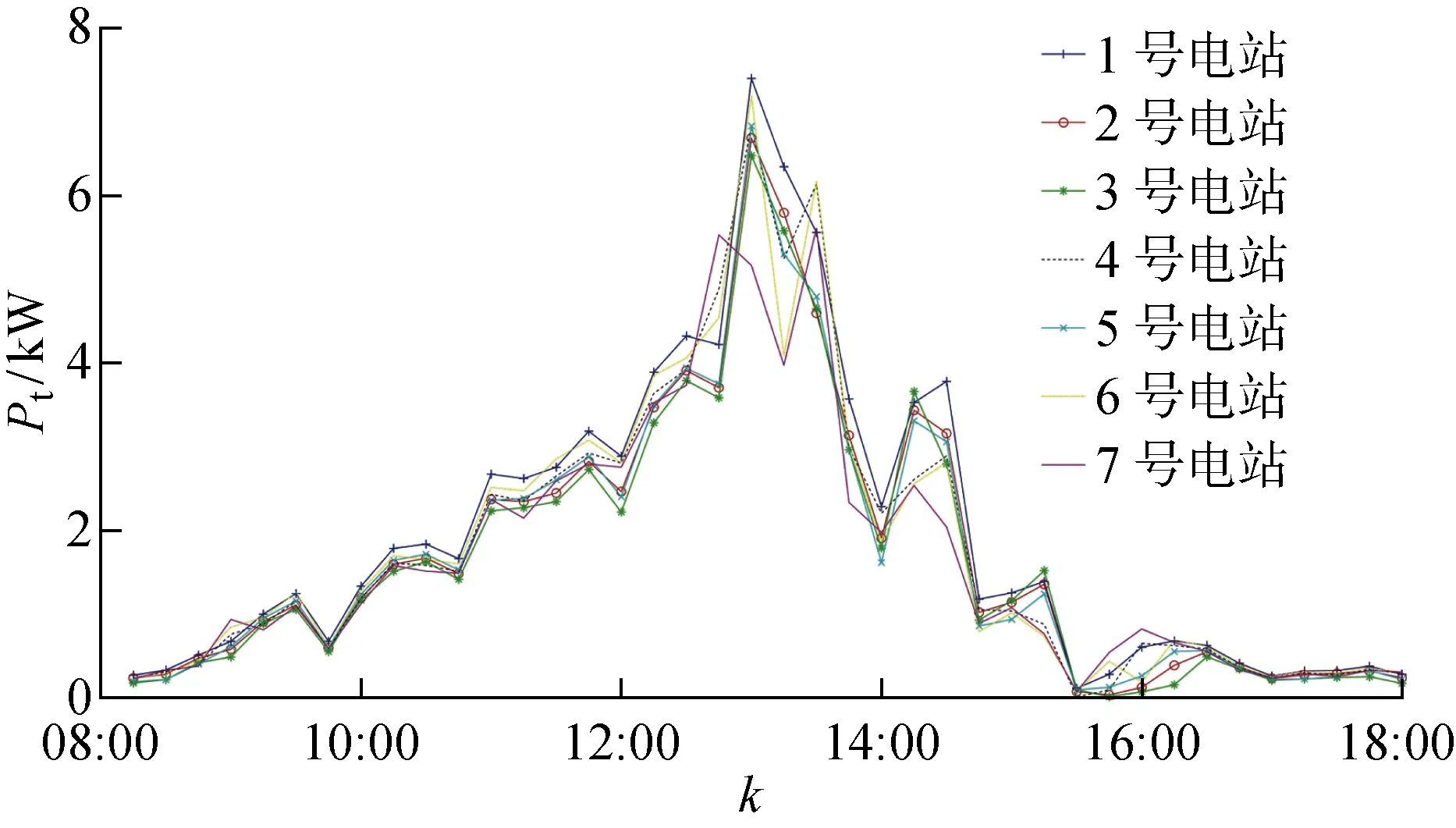
图4 电站出力功率曲线Fig.4 Output power curves of power stations

可以看出，处在相同区域内的光伏电站的出力功率曲线高度相似性，以5号电站为目标电站，分析其他电站日出力曲线对该电站的时间序列相关系数，在一个月的数据中，相关系数最小为0.76，最大为0.99，从而认为距离相近的电站有相似性.

为了探寻相似电站选取与距离的关系，选用一个更大区域内分布的电站，分别使用时序相关性与聚类方法选择相似电站.截取区域内的46个电站，装机容量皆为15 kW，电站空间分布位置如图5所示.仍然选择5号电站为目标电站，将其余45个电站与5号电站做相关性系数计算，数据量为29 d内8:00—18:00的数据，时间间隔为15 min.计算45个待选电站相对目标电站的相关系数平均值与方差，45个待选电站29 d内相关系数的方差均小于0.01，将45个电站相对目标电站的距离和相关系数平均值做线性回归，得到如图6所示的曲线.回归方程为R′=-0.003 3L+0.901 8,L为距离，R′为相关系数.决定系数R2为 0.562 8，通常，R2在 0.5～0.75时，认为存在良好的关联性.综合数据与线性回归方程，可以认为相似电站的选取与距离有关，并且对于某一个电站，距离其越远的电站相关性越弱.在本文实验数据中，对于任意电站，其1 km以内的电站的相关性均高于0.98，功率出力曲线十分相似.

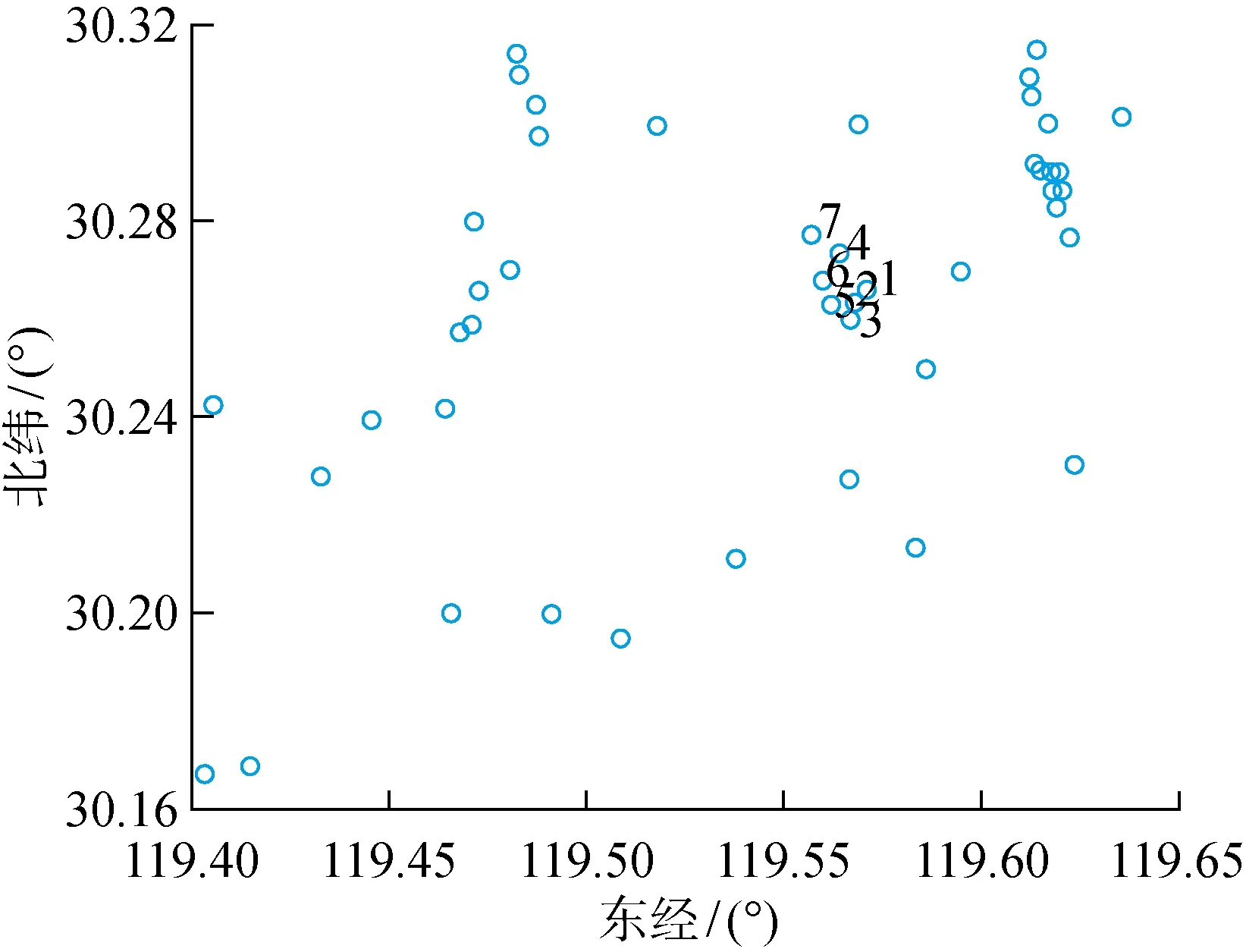
图5 电站位置分布(大区域)Fig.5 Location distribution of power stations in large area

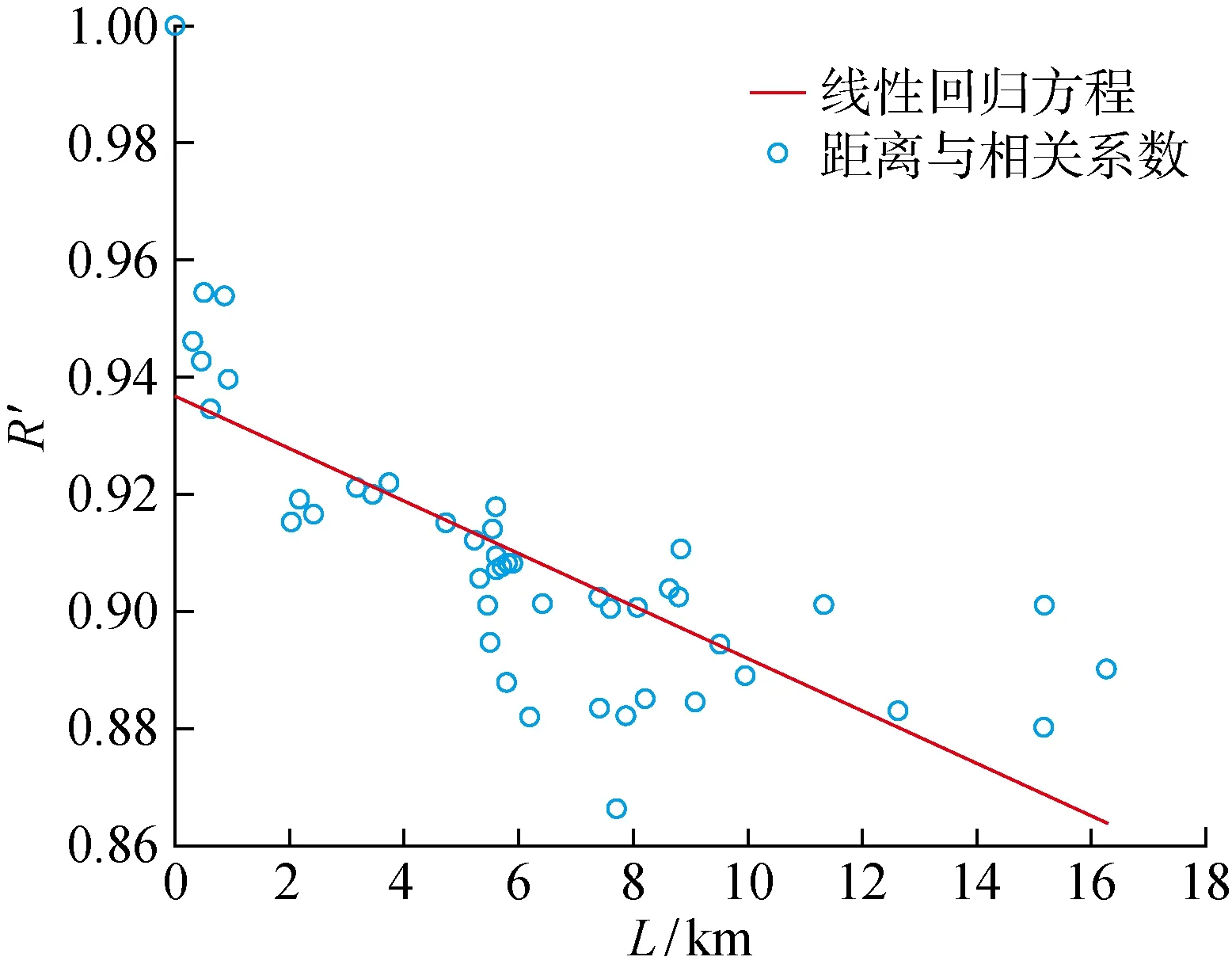
图6 距离与相关性均值的线性回归Fig.6 Linear regression of distance and mean value of correlation

为了进一步论证以上结论，使用了K-均值聚类算法对图5中46个电站29 d内的光伏出力数据进行聚类.聚类结果显示，距离为1 km内电站聚为一类的频率极高，再次验证了距离与相似电站选取的关系.综上，空间位置在1 km以内的电站出力变化不大， 在后续预测过程中对1 km以内的电站只取1个电站分析，减少算法接受的重复信息，以帮助运算.1 km为本文数据集运算的中间结果，在其他数据集上的运算结果可以不同.

2.3 电站间的时序延迟相关性分析及其影响

在距离与相关性的分析过程中，出现距离目标电站较远的电站仍有很好相关性的现象，聚类分析过程中同样出现某些电站与目标电站出力聚为一类的情况.为了探究其原因，仍以5号电站为目标电站，对某日功率曲线做相关性分析，距5号电站最远的电站距离为16.3 km，最近为0.4 km；46个电站间的相关系数最小为0.87，最大为0.99，具有足够高的相关性.选取其中3个电站的出力作为对比，其相对于5号电站的相关系数为0.87、0.91、0.96，功率曲线如图7所示.图中黑色曲线为目标电站的光伏功率曲线，红色曲线对比黑色曲线在时间尺度上有超前，蓝色曲线对比黑色曲线有滞后.考虑时间序列的延迟相关性，时间序列的延迟相关性关系[21]如下：

(10)

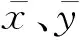
分析区域内的所有备选电站对目标电站间的时间相关性，综合相关性的变化情况选择延迟时间长度为1 h，对应图7中时间序列的4个时间点.首先对数据集中的所有时间(29 d)均做了延时相关性分析，以相关性大于0.8作为选择依据，统计出各个电站在每天相对于目标电站的延时常数后取平均值.距离与平均延时做线性回归后如图8所示，图中T1为平均时延.从图中看出，距离与延迟时间具有一定线性关系，线性回归得图中红色曲线，曲线方程为T1=0.581L+1.310 9，计算所得相关性系数为 0.685 1，认为两者间存在相关关系.计算按最优延迟或超前时间做延迟后各备选电站与目标电站间的相关性.重新做距离与相关性平均值线性回归, 得到图9所示结果.与图6相比，图9在距离较远处的相关系数有微小提升.图中线性回归所得曲线仍与图5中曲线一致，相关性系数下降至 0.357 9， 认为存在弱关系.结合距离与平均延时间的关系来看，在光伏电站的相关性分析中，由距离导致的电站功率出力存在的时间差异是距离对不同光伏电站间相关性存在差异的部分原因.

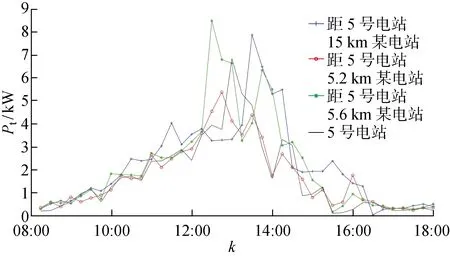
图7 4个电站的出力曲线Fig.7 Output curves of four power stations

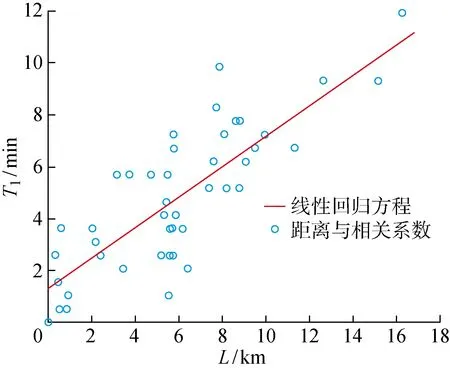
图8 距离与平均延时的线性回归Fig.8 Linear regression of distance and average delay

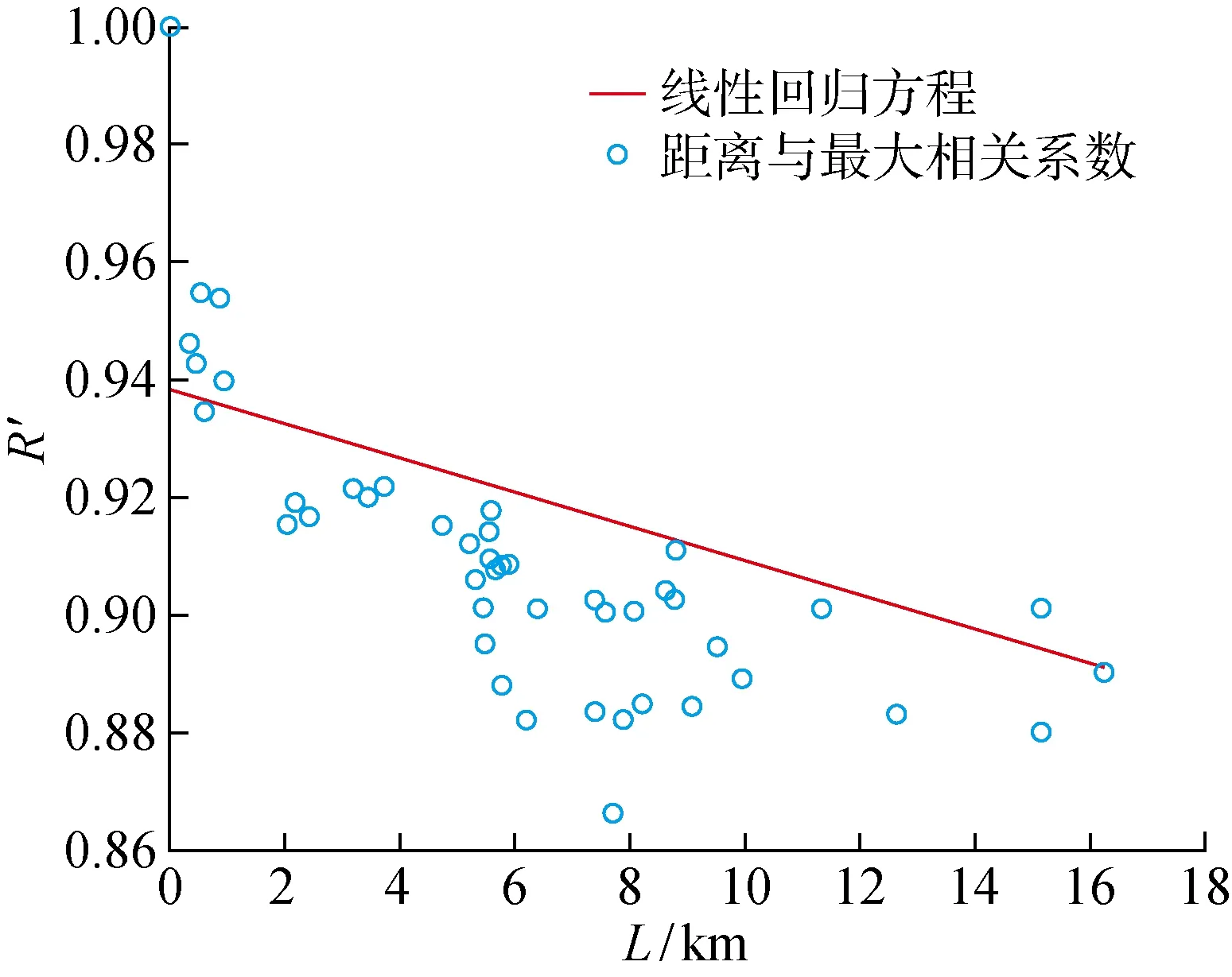
图9 距离与修正相关性均值的线性回归Fig.9 Linear regression of distance and modified correlation mean

在时序分析的过程中，距离在1 km以内的电站计算所得的延迟时间基本为0.其余相似电站的延迟时间并不相同，本文中的延迟时间是相对概念，包括超前与滞后.例如时序上超前1 h与滞后1 h均认为延迟1 h，这是因为多数电站既有超前时刻也有滞后时刻.电站间的功率出力时间序列存在延迟能够很好地帮助预测，若能找到在时序上超前目标电站的相似电站，显然会使预测工作难度下降.

2.4 气象状况与光伏电站出力的关系

光伏功率产生波动的主要原因是气象条件的不确定性，而其中主要影响为云层移动及遮挡带来的空间辐射照度变化，其他如悬浮颗粒、光伏电站安装位置及朝向、逆变器等参数的影响相对固定，在1 d内造成的变化不大.为探究云层移动带来的功率变化，选择了某日的出力回归数据，将1 km2区域作为最小单元，研究光伏电站分布位置与出力值，如图10所示，图中δ′为光伏出力占比.不同时刻的出力情况变化显示出了光伏功率出力随时间与空间位置不同而存在的差异，说明了不同位置光照强度的变化.这种差异来自于云层遮挡效应，一定程度上能够为光伏功率的预测提供帮助.由于区域内整体出力良好且有向西变化的趋势，所以可推测西南角部分(左下)接下来时刻的功率出力出现在0.6～0.8 之间.图11所示为13:15─13:30时段内区域出力变化情况.西南角部分光伏电站的出力承接了图8的变化趋势.事实上，西南角部分的电站出力情况对应图7中蓝色曲线，12:15─13:30对应该曲线中的 13:00—14:45时刻.图10和11网格为研究圈定的一个空间区域，一小格约为1 km，但由于存在一定的投影偏差，所以不做定量标度.由以上分析可知，不同位置电站功率存在的出力时间延迟或超前现象主要由云层移动造成，并且相同云层在不同时刻对太阳辐射照度的折损基本相同，从而进一步认为在相对目标电站有延时关系的相似电站中，存在着与目标电站受相同云层影响的电站.

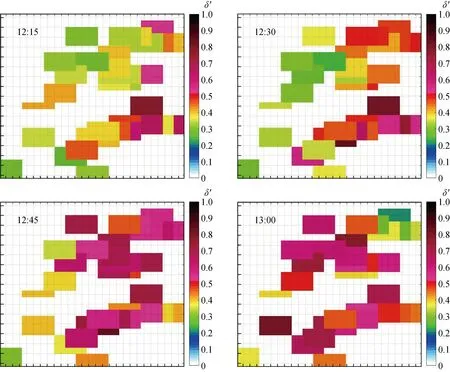
图10 12:00─13:00时段内区域出力变化情况Fig.10 Changes of regional output from 12:00 to 13:00

图11 13:15─13:30时段内区域出力变化情况Fig.11 Changes of regional output from 13:15 to 13:30

2.5 光伏出力相关性与空间位置分布

图10中，随时间推移，自东向西的出力情况变得良好，与之对应的是区域中时间延迟特性中的分析，位于目标电站西边的电站呈现出延迟，位于东边的电站呈现出超前.这种情况出现的原因与气象条件有关，选择超前于目标电站的相似电站对于预测工作是有意义的，因此在选择相似电站的过程中要考虑与目标电站的方位.

综上所述，对相似电站的选取有以下几个原则：① 距离为1 km以内的电站认为其相对目标电站恒为相似电站，其出力值可用于异常值检测或缺失值补全等过程；② 距离与相似电站的选取并无显著联系，真正影响因素为云层移动随距离远近造成时序上存在超前或延迟的特性；③ 做时序处理时，最大限度不超过1 h.特别地，云层在1 h以上的时间飘移出分布式电站所在区域，或云层发生变化从而对光资源的影响需要重新考虑.

3 数据预处理

数据因采集、传输等过程不可避免地存在缺失、重复等问题，或因数据间量纲不一致影响分析甚至导致结论错误，从而有必要做数据异常处理与归一化.基于位置相近电站出力相似的结论做数据异常值出力，基于光伏电站模型做数据归一化处理.结合光伏功率出力特点做数据预处理，从而有益于预测工作.

3.1 数据异常识别与处理

由前文可知，距离1 km以内的电站可以认为出力值相似，因此对于某个电站的缺失值进行检测并确定位置后，可选取距离1 km以内的电站将同一时刻的数据进行补充.本文中异常值的识别使用两种方法：① 装机容量使得光伏电站发电功率存在上限，检测是否存在超出装机容量的出力数据，若存在则为异常值；② 基于前文分析结论，选取某电站及其 1 km 以内的电站做相关性分析，对于相关性明显较低的电站，再次采用局部离群因子(LOF)算法检测异常值，并采用相似电站的数据替换异常值.相较于传统的均值增补方法，使用1 km内相似电站处理异常值更贴近真实数据.

3.2 归一化

晴天时，光伏功率出力曲线呈正弦形状，客观上存在的辐照强度变化规律是导致光伏出力曲线波动的原因之一，使用符合日照强度变化规律的曲线作为归一化标准，使得晴天下的光伏功率出力近似为一条直线.由式(9)可知，已知辐照强度与温度即可计算光伏电站的理论出力值.而HOTTEL晴天模型作为日辐射照度模型中的一种，对于地面所接受到的辐射有着良好的拟合效果，通常误差控制在5%，包括直接与散射辐射照度两部分.直接辐射照度Sb(β,α)的计算方法[22]如下：

Sb(β,α)=Smτbcosδ

(11)

cosδ=cosβsinh+

sinβcoshcos(ψ-ω)

(12)

式中：Sm为总辐射；τb为直射辐射透明度系数；δ为太阳光线对倾斜面的入射角；β为电池板倾斜面与水平面间的夹角；ψ为太阳方位角，从正南算起，向西为正，向东为负.式(11)适用于晴朗无云的情况，与电池板所在海拔高低相关.τb计算式为

(13)

式中：A0、A1、Ak为方程的特征系数.式(13)适用于大气能见度23 km, 海拔低于 2 500 m的情况，系数由海拔与气候类型相关，在中纬度夏季时：

A0=0.419 719-0.007 963 7(6-A*)2

A1=0.495 39+0.005 831(6.5-A*)2

Ak=0.276 522+0.018 951 6(6-A*)2

其中:A*为海拔高度.

散射辐射照度可以用下式计算：

(14)

式中：系数τd的经验公式为

τd=0.271-0.294τb

(15)

由此可由经纬度、海拔、日期和时间计算得到任意时刻某个倾斜角度时太阳能电池板水平面上的总辐射能St=Sd+Sm.值得一提的是，太阳能电池板具有倾斜角度，且依据最大功率追踪原则该倾斜角度是变化的，该数据难以获得，此处认为电池板为水平的.本文中的光伏电站出力数据为 8:00-18:00 时间段内的数据，每15 min采集一次，光伏电站分布位置在东经 119.4 °～ 119.56 °和北纬 30.12 °～30.16 ° 内，东西距离24 km，南北距离 17 km，可以认为该范围经大气层衰减后的光照强度一致.由2.1和2.2节计算所得的理论曲线如图12所示.

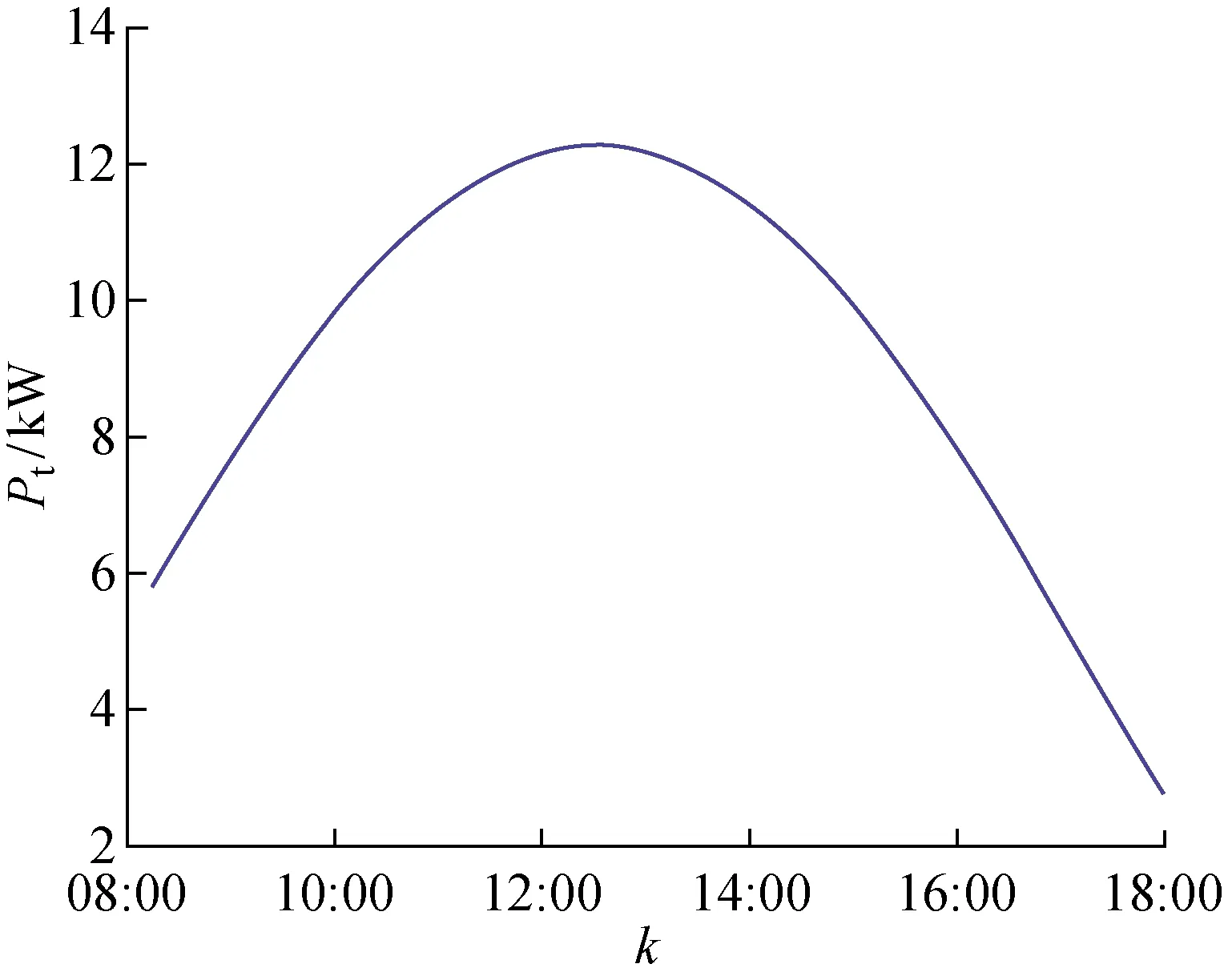
图12 理想晴天出力曲线Fig.12 Output curve of an ideal sunny day

事实上，使用HOTTLE晴天日照辐射模型所得到的光伏出力曲线在17:00─18:00的理想出力曲线在某些情况下略低于实际光伏出力曲线，可能原因有：① 模型本身的误差；② 现实中散射辐射照度并不是各向均匀同性；③ 模型本身忽略了地面反射辐射；④ 存在其他光源.其中因素②和③在直射辐射强度较大的时段可以忽略，但在直射辐射强度很小的傍晚时刻影响较大.尽管存在一定误差，但使用HOTTEL模型与光伏阵列模型做归一化方法相较于传统归一化方法在由云层移动造成的数据波动上更为精准.

4 基于时空间特性与长短期记忆网络的目标电站预测方法

基于前文分析，提出一种改进的密度聚类方法，寻找存在时间空间特性的相似电站，以此为基础设计了一种光伏功率预测算法.相似电站选取需要注意几个特性，并且认为某个电站距离较远的电站因云层移动而在时序上有前后关系.本质原因是相同的云层对太阳辐射强度的遮挡情况一致，当云层在分布式光伏发电所在的区域内移动时，当前受其遮挡效应影响的电站的功率与之前受影响的电站间的光伏功率出力会有相同的下降幅度，而在云层移开时有相同的上升幅度.基于这种特性，结合前文分析论证结果，综合设计了一种寻找时序上对于目标电站有先后顺序的电站，进而通过出力状态的预测反推出天气可能的变化.

4.1 基于改进聚类算法的出力特征匹配算法

归一化后的数据最大限度反映了云层移动对各位置电站功率出力的影响，相同的云层经过造成的上升与下降的幅度大致相等，云层遮挡时出力降低，云层移开时出力上升，呈倒三角状.目标电站的出力波动在过往时间段内出现在周围电站上，期望寻找到有延时的相似电站，将其作为预测依据.由此提出一种改进的密度聚类方法.聚类算法中用数据间的距离为聚类提供依据，常用的距离有曼哈顿距离、欧氏距离、余弦距离等，基于相同云层造成出力波动相似结论，要求聚类所得曲线在距离、轮廓上均要相近.余弦相似度是评价向量间轮廓相似度的有效工具，提出引入余弦相似度改进向量A、B间的距离公式：

(16)

式中：Ai、Bi为向量A、B的元素；b为偏置量，本文取0.1.

改进距离公式做聚类的结果相较于欧氏、曼哈顿距离有效剔除了轮廓不相似的结果，缩小了相似电站的选取范围.选用密度聚类的原因[23]在于找到整个区域内与目标电站出力相似的电站群，概率上大范围的相似电站群预测更为精确，对于其中与目标电站相似很高的离群点电站，仍可进一步考虑，从而改进密度聚类算法流程(扫描半径Eps为聚类算法中需要设置的一个阈值).

(1) 选定目标电站A，截取当前时刻t至t-4时刻值为At，其余备选电站截取t-1时刻至t-5时刻为Bt.

(2) 设定最小包含点数(Minpts)与Eps为密度聚类算法提供参数, Minpts由空间电站分布决定, Eps考虑HOTTEL模型5%误差，留出裕度选取为0.15.

(3)At作为聚类中心在Bt中寻找小于Eps的电站集合E.

(4) 采用密度聚类算法对这些电站进一步聚类分析，在原有的改进距离公式上进一步加入权重值：

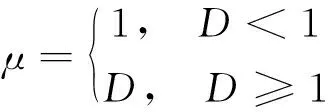
(17)

式中：D为当前聚类点与其余聚类点之间的距离.

(5) 经过密度聚类算法，综合计算相对电站的均值，选取均值最小的类作为一组相似电站.在预测算法中将对目标电站改进距离最近的电站的t时刻功率出力作为目标电站t+1时刻的功率预测值.

4.2 基于时空特性的目标电站出力预测方法

如图13 所示，改进密度聚类选择时间上有延迟特性的相似电站做预测，预测的精确程度取决于所选择的相似电站在现实上是否真正与目标电站受相同云层影响，并在时间上有先后顺序，仅使用改进密度聚类算法很难确定.例如空间上存在的云层在短时间内发生形变、重叠等变化，使得不存在Eps小于0.15的电站.为了解决以上问题，可适度扩大阈值Eps，并设立上限以保证精度.本文取Eps上限为0.4.此时仍无法选择电站时，取上一时刻目标电站周围电站出力的均值作为预测值.因此算法中部分点不可避免的存在误差，尽管在Eps选用0.4时少有无法选择电站的情况，然而增大阈值的方式会难以获得真正的相似电站，从而进一步增大了误差.

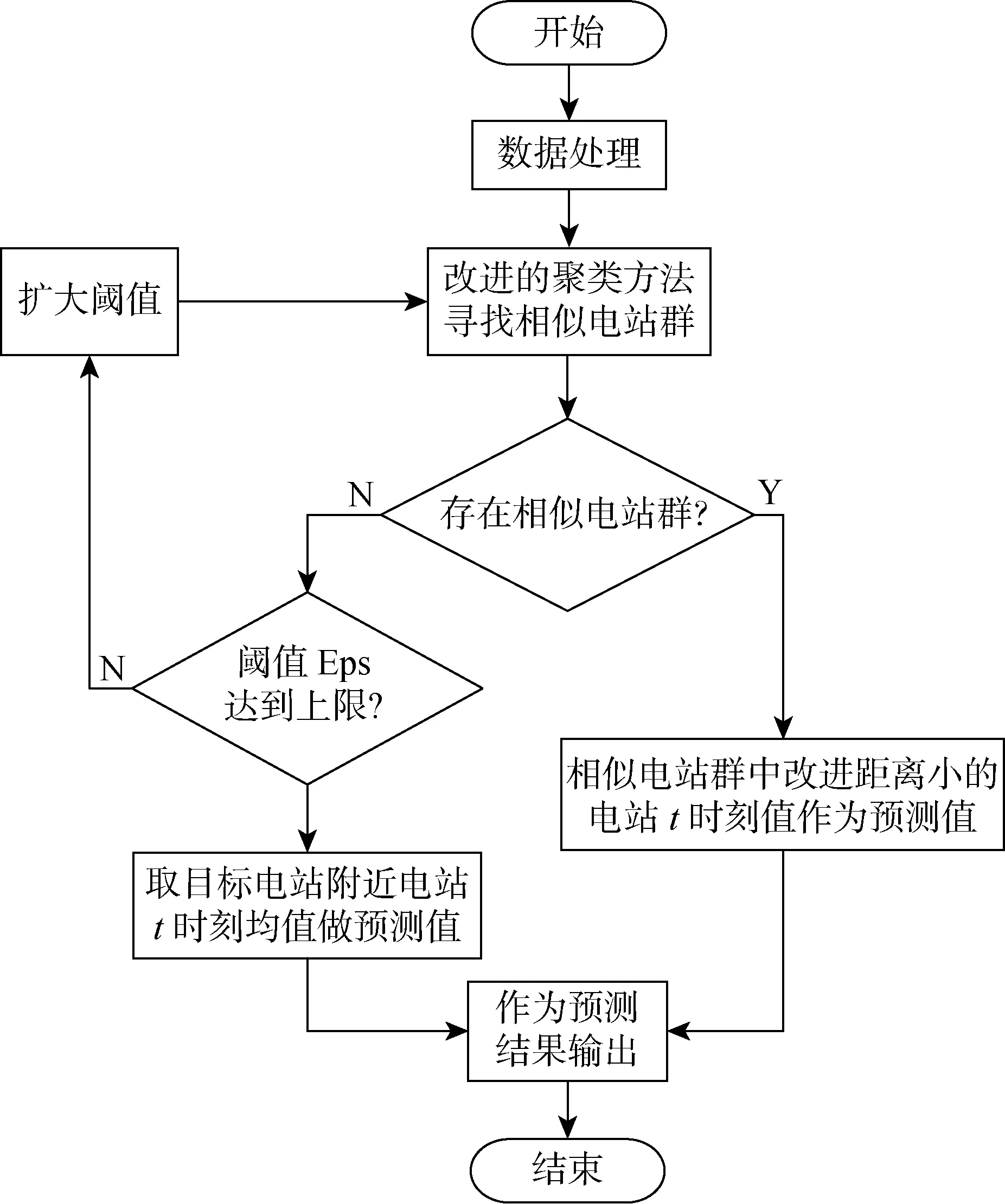
图13 基于时空间特性的光伏出力预测方法Fig.13 Photovoltaic output prediction method based on time and space characteristics

4.3 长短期记忆神经网络优化

长短期记忆(LSTM)神经网络[24]是一种基于循环神经网络(RNN)改进的深度学习算法，尤其对处理时序数据有很好的效果.LSTM继承了RNN的递归属性，充分利用时序数据的同时，也弥补了RNN 梯度消失和梯度爆炸以及长期记忆能力不足的缺点.使用考虑时空特性的目标电站预测算法后，将每日得到的预测值作为数据输入，实际值作为输出，使用LSTM去除由HOTTEL模型、温度等其他随时间变化因素带来的误差.基于前文分析，提出了一种依据时空间特性选择相似电站的方法，并进一步提出一种光伏功率预测算法，相较于同模式的其他光伏功率预测算法，本方法的创新之处在于：① 引入了辐照模型与电站模型，提出更适合光伏功率出力的归一化方法；② 提出了一种改进的聚类距离公式，公式兼顾了聚类向量间的欧氏距离与轮廓相似度，缩小了相似电站的选取范围；③ 采用延迟时间方式选取得到相似电站的时空间特性明确，有利于预测工作进行；④能够在一定程度上给出预测是否精确的提示，为调度安排提供准备时间.

5 仿真分析

鉴于国内目前海上漂浮式光伏工程的缺失，验证数据由浙江国家电网合作提供，包含浙江省杭州某地区几百平方千米一个月内的分布式光伏电站的功率数据及其电站的装机容量.数据中的信息时间段为08:00─18:00的功率数据，每15 min采集一次，故1 d内数据点为40个.经由异常处理后，2018年6月3日因数据缺失严重不予使用，从而数据集共有29 d的115个电站数据.此外查询了2018年6月份的天气情况，全部为阴雨或多云天气，每日温差最高为11 ℃.

如图14所示，在选定目标At与时间上相差为 15 min 后的Bt，即不做归一化，以欧氏距离使用K-means聚类得到聚类段，以期寻找在不同时间段内受相同云层影响的电站作为相似电站.聚类段4相对目标段更符合云层在不同位置移动造成的变化，但功率大小有明显差异，这是因为当前时刻t为 13:00，此时辐射强度氏于聚类段所在的12:45时刻，造成了距离上的差异.此外，聚类段4所在电站可作为有时序特性的相似电站，然而在欧氏距离上聚类段1却是最近的，这体现出仅使用欧氏距离选择有时序特性的相似电站有极大困难.表1所示为其距离与电站标号对应的聚类段.

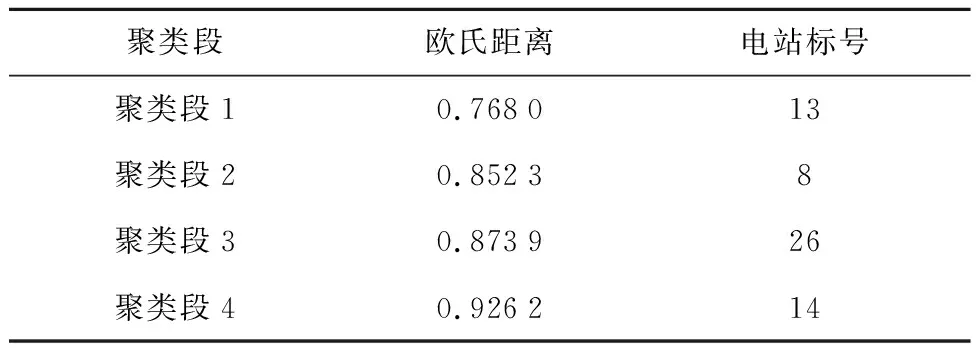
表1 未归一化聚类算法所得聚类段Tab.1 Clustering paragraphs obtained by unnormalized clustering algorithm

如图14所示，未经归一化使得因辐射照度变化在聚类过程中影响着欧氏距离的计算，同时干扰特征匹配的精准度.在图15中的最优聚类段对应的电站标号为14，在表2以及图15中同样聚类得到了14号电站.这体现了使用归一化方法能够很好地消除辐照强度随时间变化带来的因素，并且还得出更符合特征匹配要求的16号电站.在形状上，聚类段1与目标段有良好的对应关系，且其在时序上超前目标15 min.改进距离公式客观上增大了形状不相似间向量的距离，从而更为有效地选取受相同云层影响的电站.选定某个电站，使用图13中基于时空间特性的光伏功率预测算法对数据集中的29 d做光伏功率预测，图16所示为其中2 d的功率值以及对应预测结果.

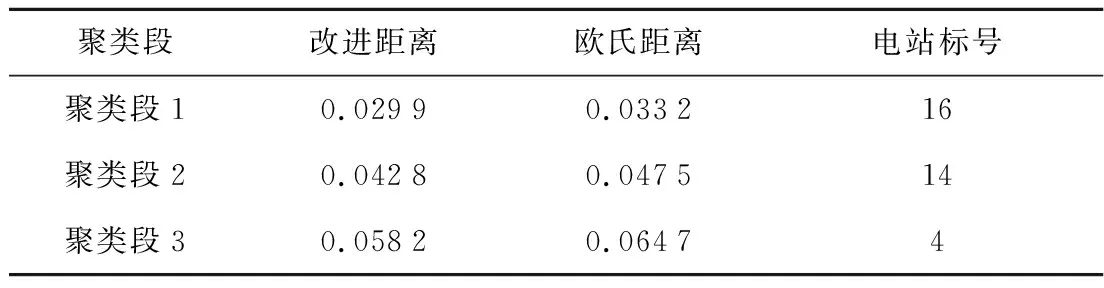
表2 归一化后改进聚类所得聚类段Tab.2 Clustered paragraphs obtained by improved normalization clustering algorithm

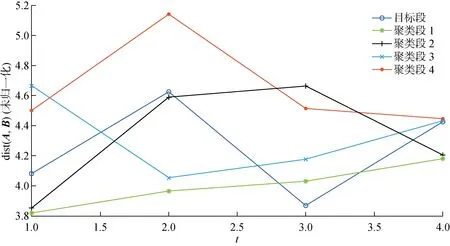
图14 某时间段K-means聚类效果图Fig.14 Effect of K-means clustering in a certain period

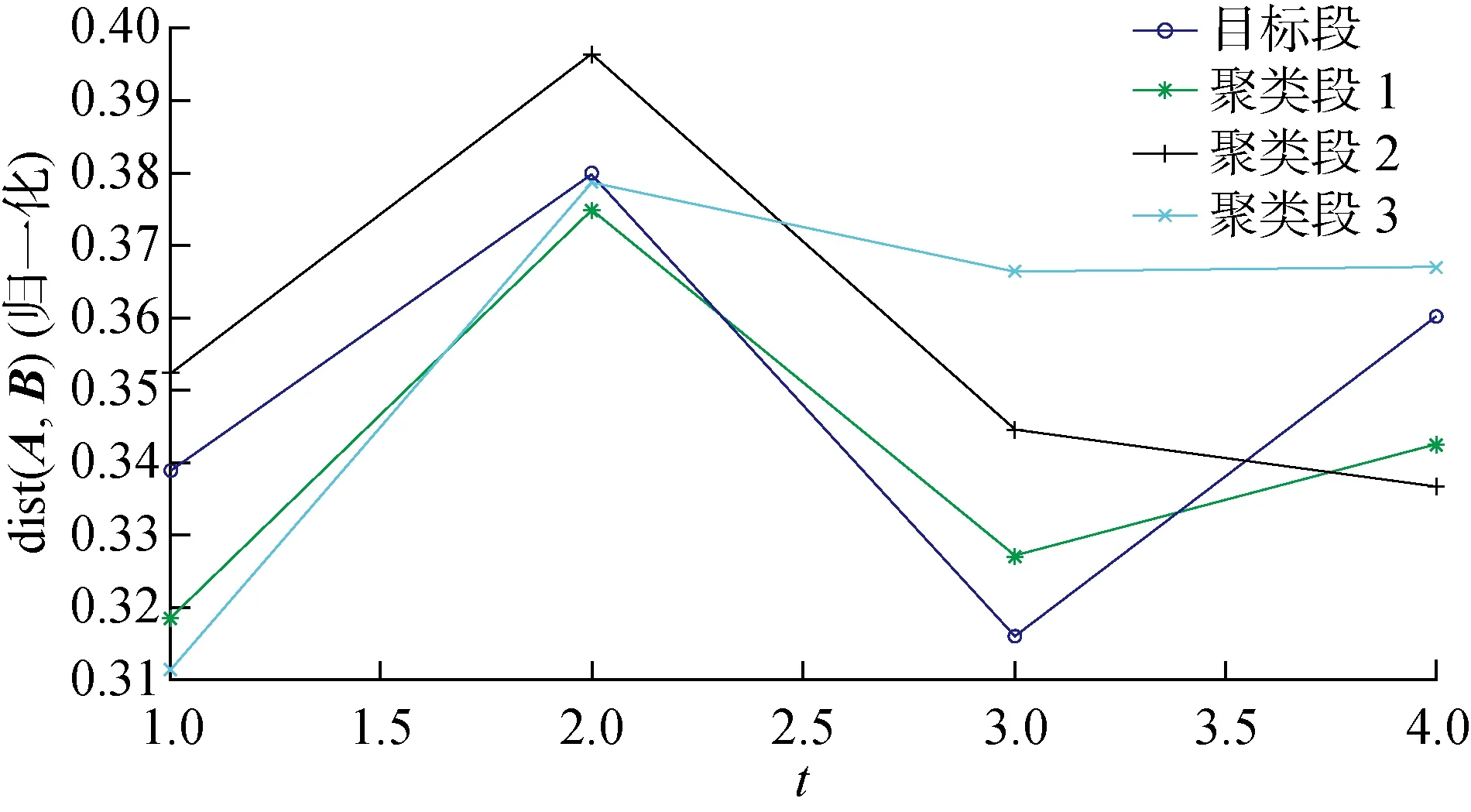
图15 改进聚类效果图Fig.15 Improved clustering effect diagram

29 d内全部预测值与实际值间的均方根误差(RMSE)如图17所示，经由LSTM神经网络优化的部分结果如图18所示.图16～18预测结果在大部分时间段内的预测值精度较高，但在部分时序的预测仍有差别，这些误差的来源是：① 在建模过程中所使用的光伏电站模型仅考虑辐射照度造成的差别，忽略了温度、电池板倾角等其他因素，所使用的太阳辐射照度计算模型本身有5%误差，且不计最大功率跟踪问题；② 算法中Minpts、Eps参数的不合适选取, 使得难以聚类到相似电站，并且本身区域内有多个对光资源有相同影响的云层移动，使得相似电站难以确定；③ 区域内气象变化过于剧烈，在一个采样点15 min内该区域气象完全发生变化；④ 电站与电站间地处海拔、周边环境、板面积灰等其余因素造成的误差.LSTM神经网络在一定程度上具有优化功能，但对于优化前预测精度较高的情况优化结果十分有限，表3所示为部分日优化对比.

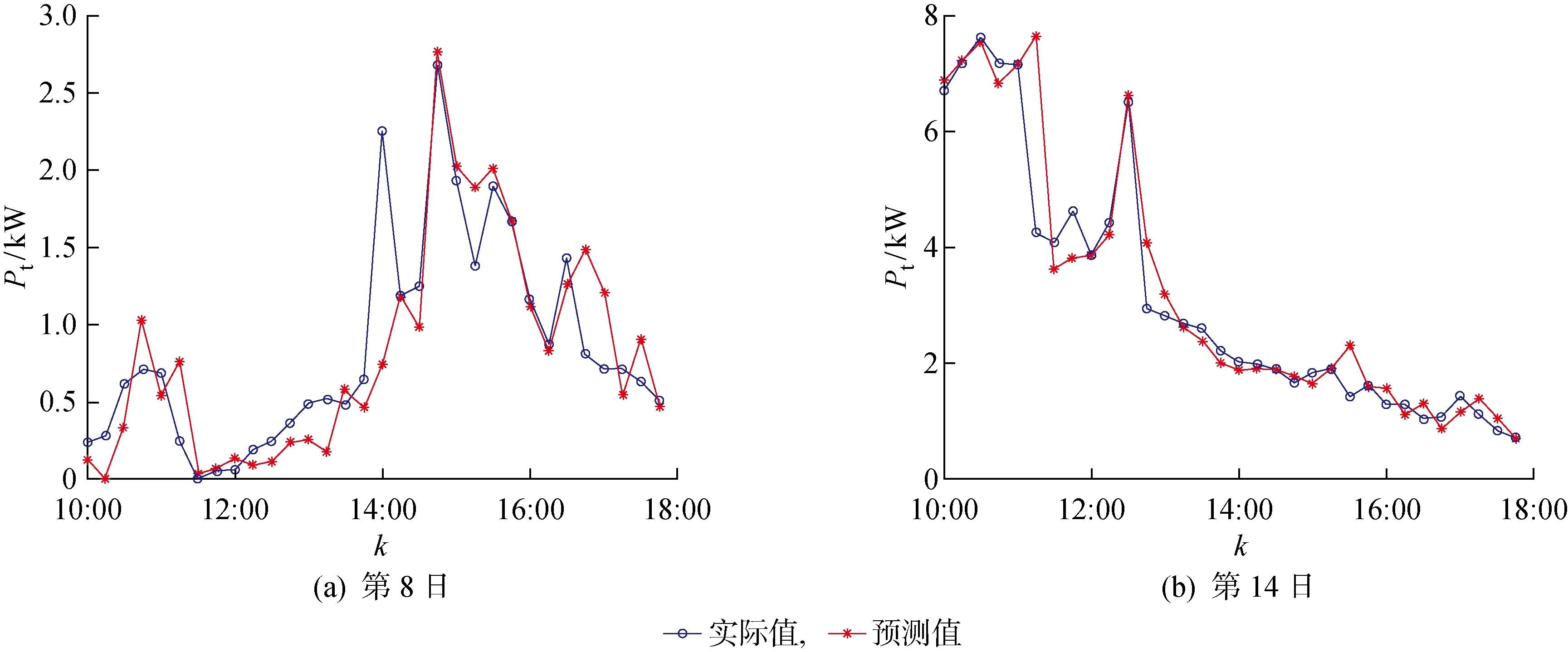
图16 第8日及第14日预测结果Fig.16 Forecast results of the 8th and 14th day

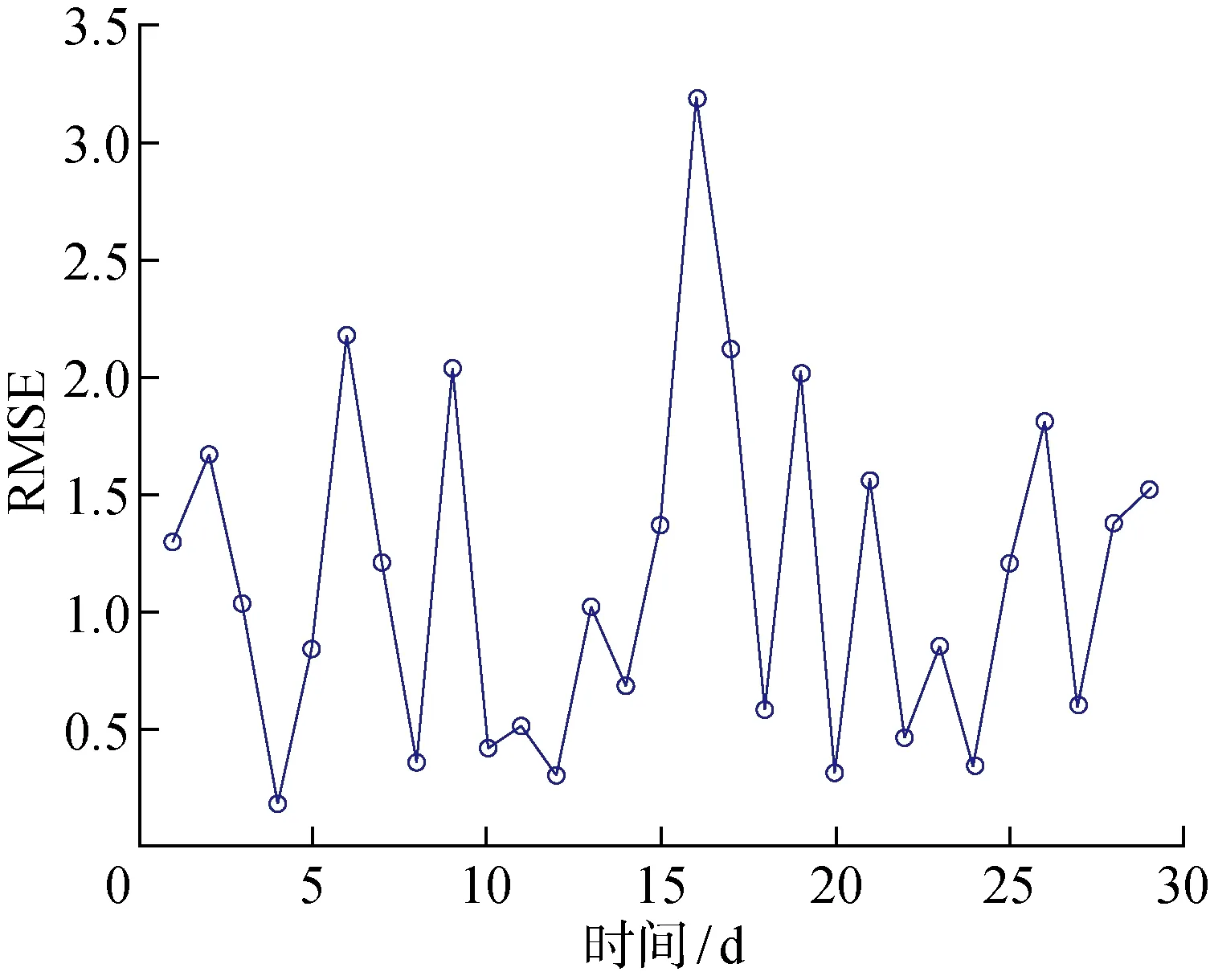
图17 29 d的RMSE分布情况Fig.17 RMSE distribution at 29 days

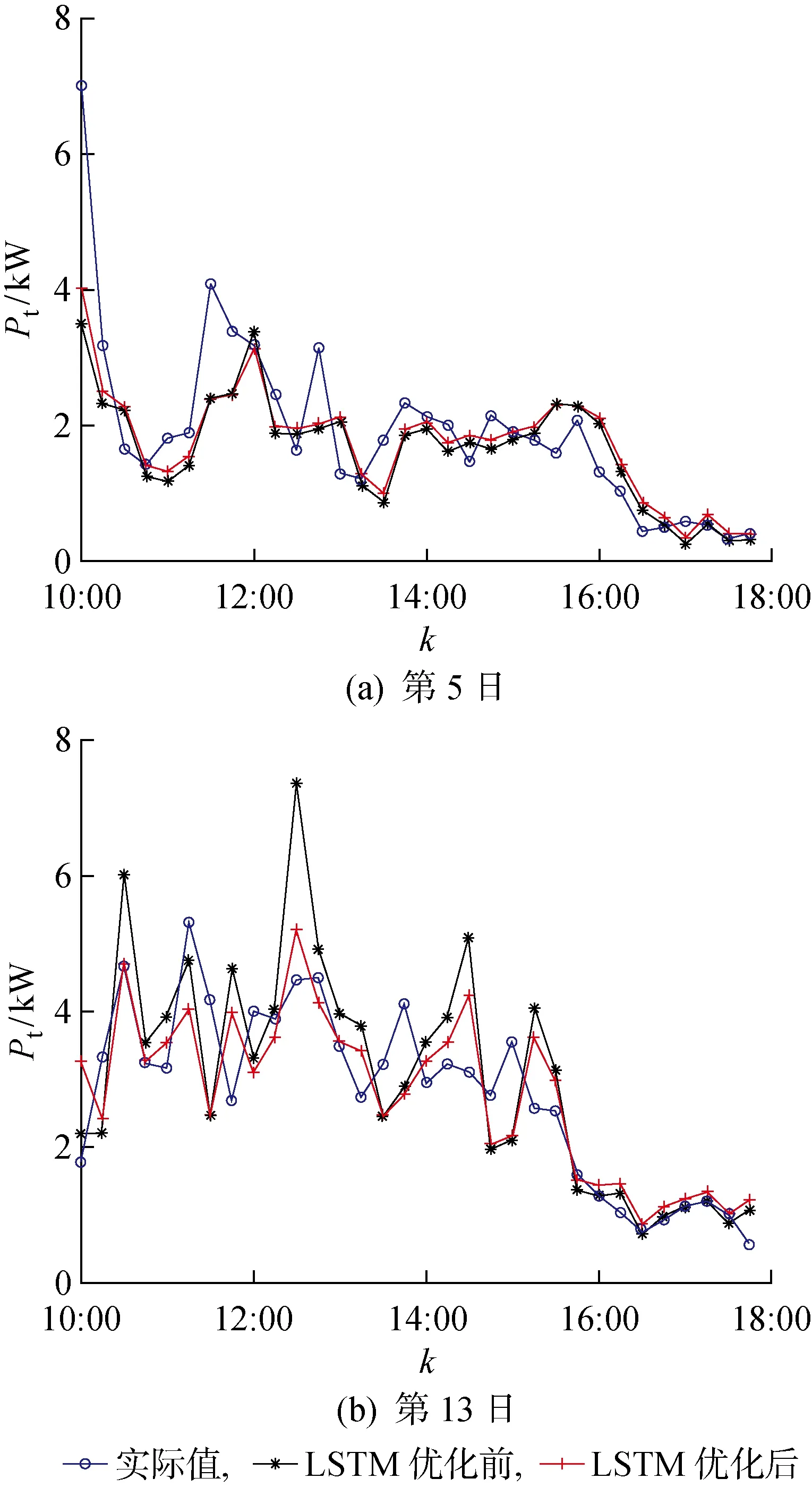
图18 第5日和第13日优化结果Fig.18 Optimization results of the 5th and 13th day

如表3所示，第16日预测结果为23.14%，误差在15%以上，优化后为14.35%，幅度为8.79%，预测优化幅度在7%～9%之间.但是对于原本预测结果在8%以下的情况优化幅度有限.要进一步开展优化需要从更为完整的数据集入手， 同时从时空特性出发研究更为精确的机理模型来针对部分气象变化剧烈的情况.同时本方法对分布式光伏电站的分布提出一定要求，目标电站的周围各个方位在一定距离内均需要有足够数量的电站才能够使得预测精准，这对于海上漂浮式光伏网格系统是完全可行的.但对于定性的气象突变感知及预警，已经达到要求.

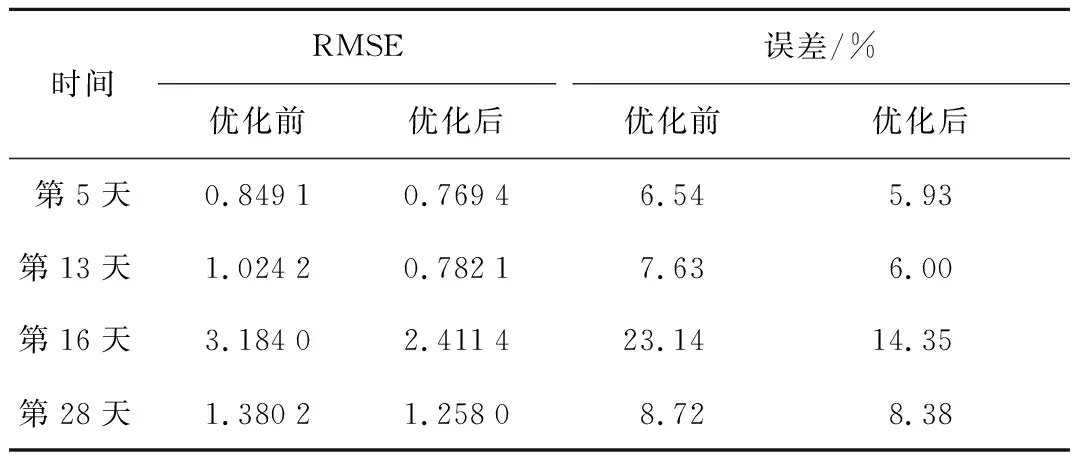
表3 LSTM优化前后RMSE对比Tab.3 Comparison of RMSE before and after LSTM optimization

6 结语

建设海上光伏系统并实现网格化有利于实现海上牧场等场景的无人化管理，不仅表现在有关机器人的电力供给，还可以作为传感器感知海上复杂的气象变化，让系统及时针对性地作做出预警保护反应.本文通过基于时空间相关性的相似电站研究，采用信息融合得到目标位置的预测出力，首先通过因素分析以及数据统计得出待预测区域内的一般规律，针对因客观云层移动带来不同位置间电站功率出力的变化，设计了一种改进距离的密度聚类算法，并依旧算法设计出一种预测方法.通过仿真算例验证了基于时空间相关性的目标电站预测方法在预测精度上有良好表现，进而可以完成突变天气预警要求的感知任务.所提研究思路可以在一定程度上克服传统基于数据驱动的光伏预测算法的黑箱-过拟合缺点，且面向的海上突变天气的感知-预警问题要比可再生能源并网对电力系统的冲击问题有更高的误差裕度.这种预警在时间上的提前量主要是由应用场景的最低要求决定的，可以由光伏网格规模等因素充分调节.主要结论在面向4级及以下海况条件有效，更复杂的风浪条件有待验证.