基于GA-ACO优化BP算法的齿轮箱初期故障诊断研究

庞晓霞，王 强，张 峰

（1.郑州城市职业学院智能制造学院，河南 郑州 452370；2.河南科技大学信息工程学院，河南 郑州 452370；3.河南新志通信工程有限公司技术部，河南 荥阳 450100）

齿轮箱在动力传输部件中获得广泛使用，可以快速完成传输载荷和转速的精确调节，对于保障机械传输结构的控制性能发挥了重要作用［1］。考虑到齿轮箱通常需承受高载荷的高速运行工况，面临恶劣的外部环境，极大提高了故障概率，也是造成机械设备运行故障的关键原因。对机械运行过程产生的各类故障进行统计分析发现，接近15%的故障都是由齿轮箱引起的。为确保机械部件运行安全性，越来越多的学者都开始关注齿轮箱故障诊断方面的新技术开发，对提升工业动力系统整体控制性能也具有较大意义。

赵艳丽等［2］则在齿轮箱故障诊断过程中加入了模糊关联的方法，同时根据隶属函数获得每个参数隶属度数据，能够准确识别出齿轮箱发生表面磨损、局部点蚀、组织交联或断齿等故障问题；Liu 等［3］通过粒子群优化算法确定信号特征，经测试发现该算法可以实现故障的高效诊断；杜设亮等［4］提取得到10 种故障参数，同时建立了组织体系BP 算法，可以准确诊断齿轮箱产生的4 类主要故障；王凯等［5］选择小波神经网络的处理方法诊断齿轮故障；Chen 等［6］同时利用粗糙集理论和神经网络进行信号数据处理，可以高效诊断出旋转机械运行故障特征；艾利等［7］开发了一种以GA 与BP 算法对故障进行快速分析的新算法，同时设置权值与阈值作为自变量，经迭代计算获得最优解，达到训练BP 算法的效果，能够精确诊断齿轮箱故障问题。

为了同时提升算法处理精度及收敛效率，本研究针对BP算法实施优化，设计得到一种通过GA-ACO方法对BP算法优化算法。根据蚁群算法确定神经网络的最优权值与阈值，再利用上述优化结果组成BP算法，并诊断不同结构齿轮箱运行故障信号。相对蚁群优化神经网络，GA-ACO优化BP可以更加准确诊断故障，并缩短了处理时间。

1 齿轮箱振动特征分析

1.1 齿轮箱振动机理

齿轮箱发生振动时呈现明显的非线性运动特性，需要构建复杂的振动模型。为了更高效分析齿轮箱振动作用机制，需建立简化结构的齿轮副模型［8］，从而便于分析齿轮箱故障。简化模型的具体结构如图1所示。

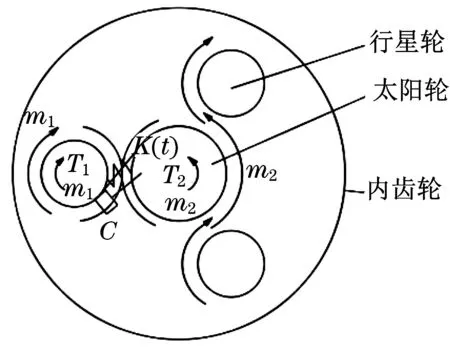
图1 齿轮运动模型Fig.1 Schematic algorithm of gear motion model

将模型运动过程表示成以下的形式：

式中：M为等效质量，M=m1m2/（m1+m2）；C为啮合阻尼；x为齿轮运行位移；k（t）为啮合刚度；E1为静弹性变形；E2（t）为故障函数。

1.2 齿轮箱信号分析

根据齿轮箱振动信号判断运行状态，可获得比其他故障判断方法更高效的结果。通过振动信号诊断齿轮箱故障前，需从振动信号内选择有价值的特征信号。为满足以上要求，需对齿轮箱振动信号分别从时域与频域2个层面开展全面分析。

结合前期研究结果可知，在出现初期故障的情况下，受到峭度与裕度的显著影响，而当故障经过一段时间推移后，出现了稳定性降低的现象。峰值与偏态指标虽然在初始阶段不具备较高的敏感度，但可以保持良好稳定性。利用上述特征共同诊断故障时，有助于模型达到更高的故障识别准确率。

不同频率下的变化幅值与相位参数不同，频域特征指标包含相关因子与谐波因子，具体计算公式如下：

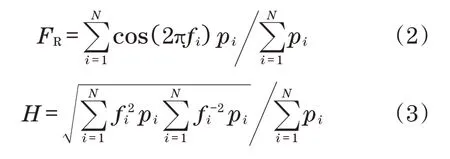
式中：fi为i时刻功率谱频率；pi为i时刻功率谱变化幅度。

2 GA-ACO优化BP算法

第1 步利用GA 算法进行寻优计算，获得BP算法的最优权值与阈值；然后，对信息素分布实施初始化，使优化解路径上形成更高浓度的信息素，促使ACO 搜索过程获得更快收敛速率并提升结果精度。

根据如下公式完成信息素初始化：

式中：τG为经过GA 寻优处理得到的信息素浓度；c为信息素恒定值。

第2 步以GA-ACO 对BP 算法优化的过程如下：

首先，对BP 算法与蚁群参数实施初始化；然后，S只蚂蚁进行信息素的数据搜索与更新。由蚂蚁确定之后的节点，直至所有蚂蚁搜索过程结束。搜索过程中，蚂蚁可以通过如下公式对各边信息素实时更新：

式中：P为信息素挥发系数；Δτj为在j元素路径上产生的信息量。

第3 步将遗传算法融入蚁群算法中。完成蚁群的交叉与变异计算后，得到新个体计算式：

式中：x为蚁群的后一路径节点。

利用式（6）得到适应度，并判断是否符合最优解条件。当结果符合时将其代到第4 步，反之则代到第2步。

第4 步根据上述蚁群算法寻优所得的结果对BP算法进行训练，得到误差e，存在以下关系：

式中：Oq为期望值；Yq为预测结果；q为神经元数量，q取值为1，2，…，n。

第5 步结合上一步结果对BP 算法权值与阈值进行更新，分析结果是否符合要求。当结果符合判断条件时算法结束，并确定故障特征；反之跳转到第4步。

GA-ACO优化BP算法流程如图2所示。

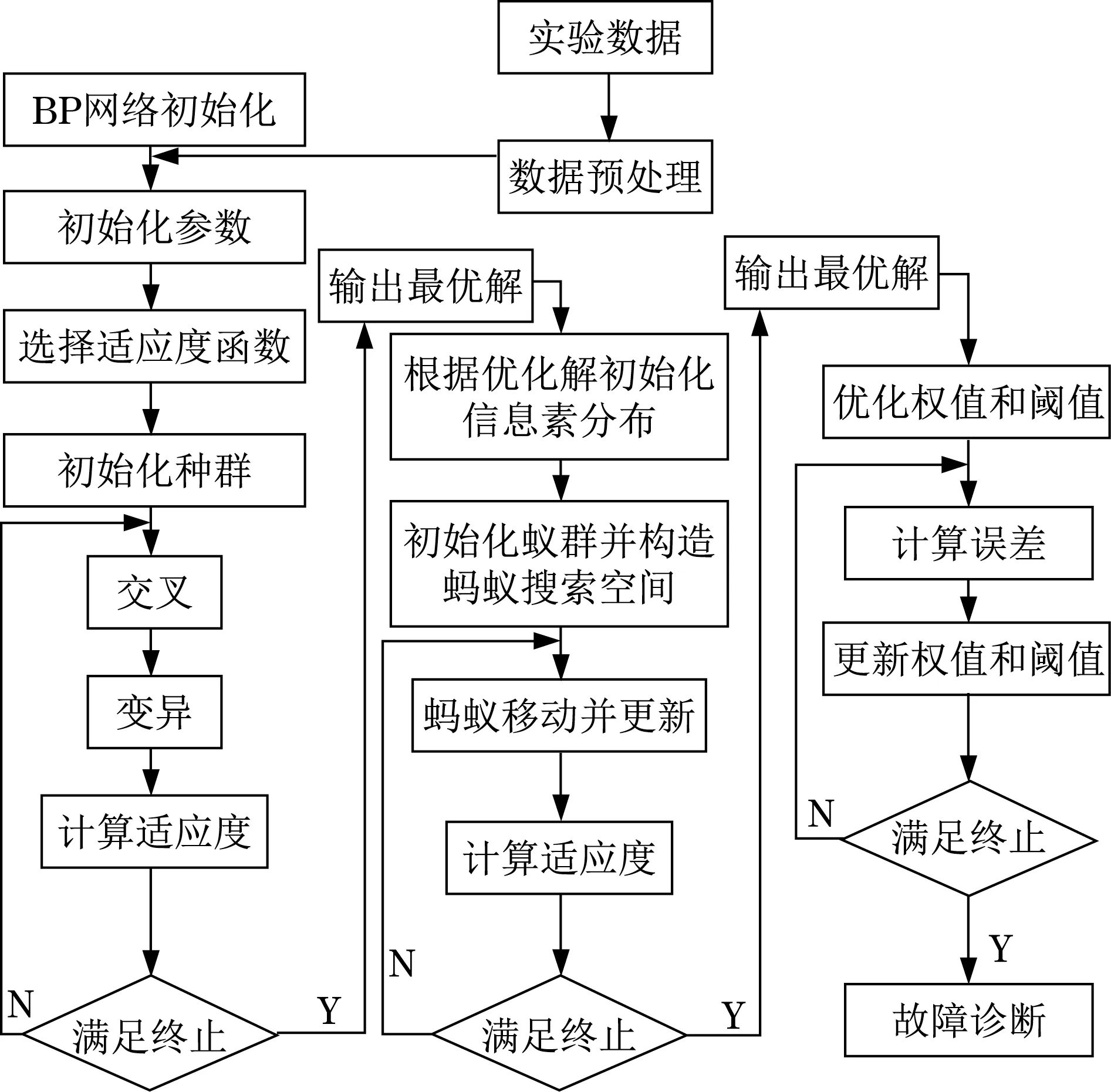
图2 GA-ACO优化BP算法流程Fig.2 Flow chart of GA-ACO optimization BP algorithm

3 实验结果分析

3.1 实验方案

本研究从某故障诊断平台上采集各项故障数据，分别测试了点蚀、表面磨损、断齿与正常运行参数。测试平台与故障测试过程如图3所示，测试得到的初始信号如图4所示。

图3 实验现场示意Fig.3 Schematic diagram of experiment site

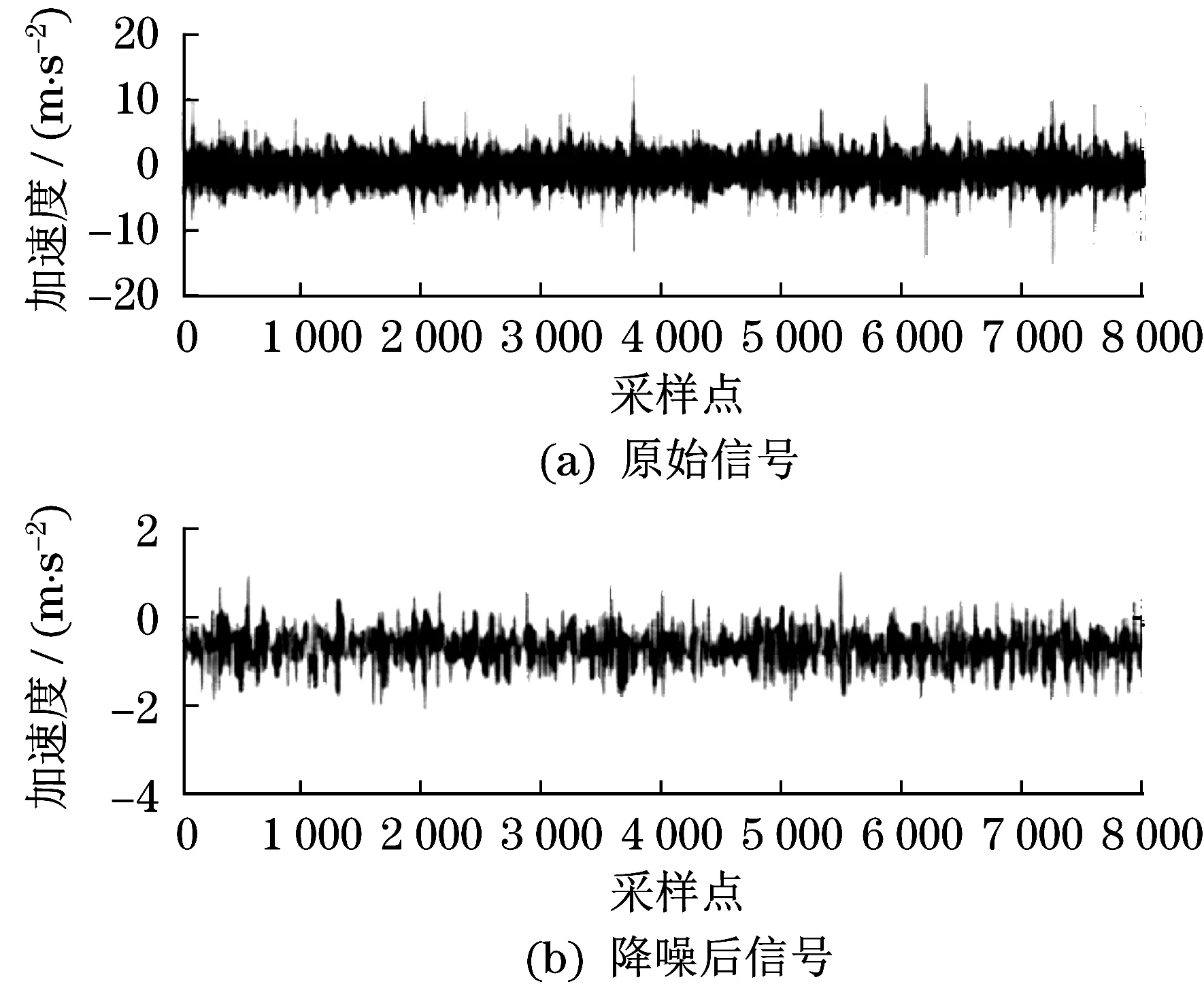
图4 小波变换降噪前后对比Fig.4 Comparison of wavelet transform before and after denoising

为同时提升模型收敛速率与精度，应对以上各项特征值实施归一化，得到训练、测试样本见表1和表2。根据表1和表2可知，齿轮箱主要形成了5种不同模式，包括4种故障与1种正常的运行模式。

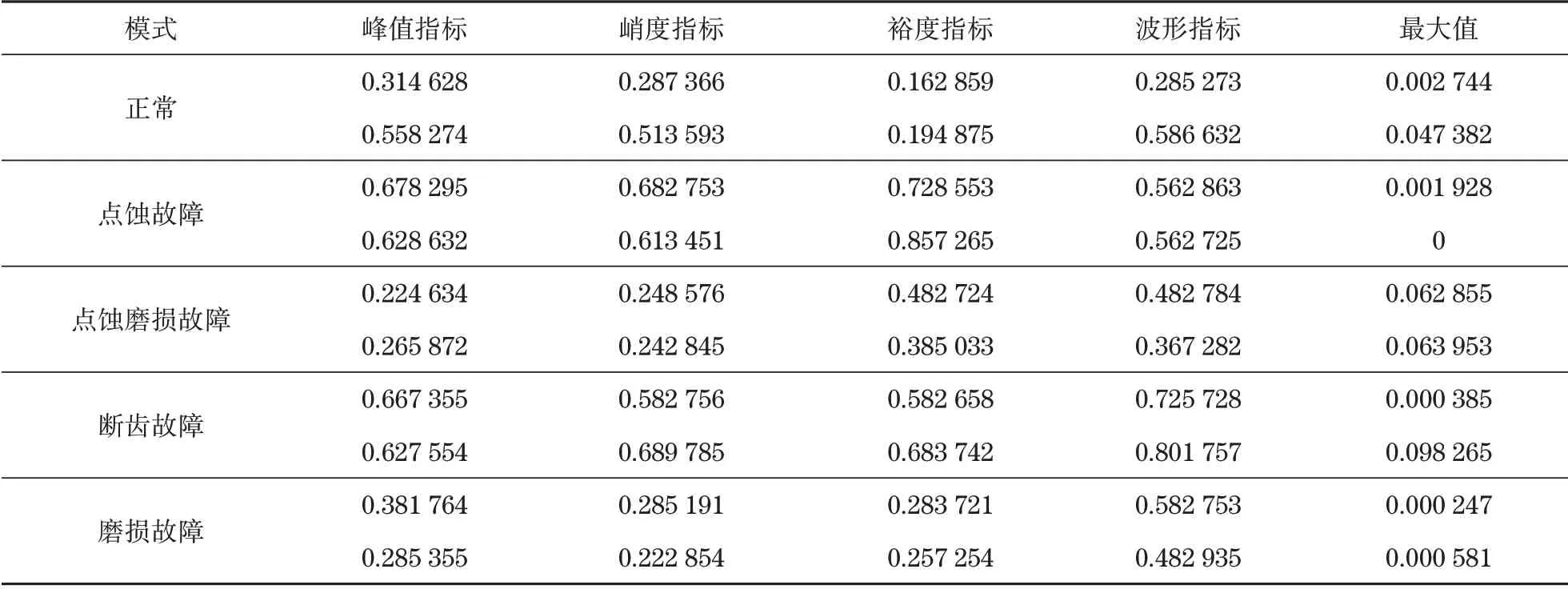
表1 训练样本特征值归一化Tab.1 Normalization of eigenvalues of training samples

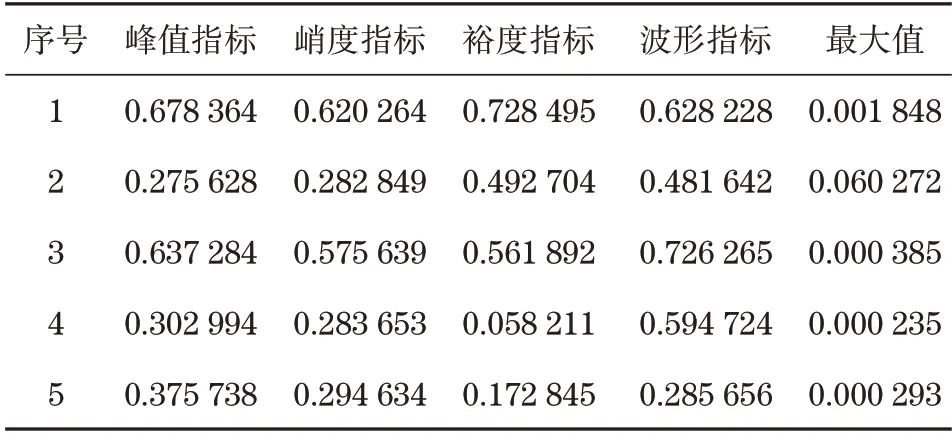
表2 测试样本特征值Tab.2 Test sample eigenvalues

3.2 神经网络建立及参数选择

可以通过3层神经网络完成n维至m维之间的函数映射，设计5-11-5网络。学习率0.01，目标误差0.001，迭代上限1 000。利用函数Sigmoid激励隐含层与输出层，以Trainlm作为训练函数。将GA种群设置在50，迭代上限为100次，交叉率0.6，变异率0.01，到达迭代数量上限时进化过程停止。设定蚁数目S为50，信息素挥发系数ρ为0.02，目标误差E为0.01。

总共选择10组参数对神经网络进行训练，各工作状态分别设置了两组，单组数据中包含了5个特征值。共设置50个特征参数实现神经网络的训练过程。输入向量是包含50个特征向量的矩阵，其大小为5×10。

3.3 2种算法效果比较

以GA-ACO对BP算法优化后再完成样本的训练过程，总共迭代20次获得图5中的训练结果，各项参数见表3。对表3进行分析可知，模型实际和期望输出形成了相近的故障诊断结果，误差0.000 185，满足目标控制标准。以上结果表明，对BP 算法实施GA-ACO优化处理后，可以对齿轮箱故障达到很高的诊断准确率。

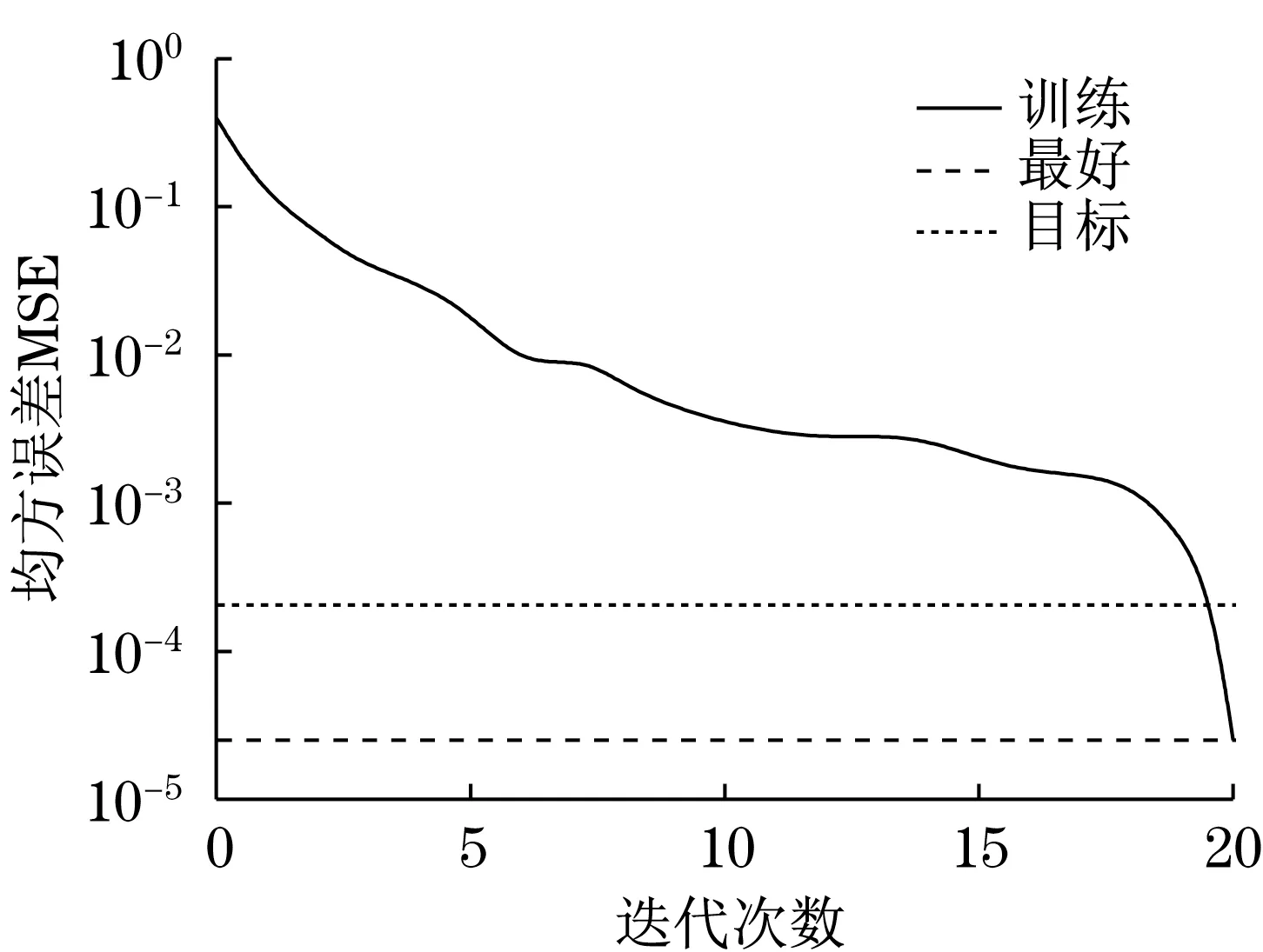
图5 GA-ACO优化BP算法训练结果Fig.5 Training results of GA-ACO optimization BP algorithm

表3 GA-ACO优化BP算法故障诊断输出Tab.3 GA-ACO optimized BP algorithm fault diagnosis output

对比本文2 种算法诊断性能，保持各项参数不变的条件下，以ACO 优化BP 算法实施训练。迭代61 次后，获得训练误差为0.000 965。以ACO 优化后BP 算法可以准确识别齿轮箱故障，测试误差只有0.013 8，未达到本文设计方法的性能。

测试结果差异性见表4。根据表4可知，同样的测试与训练数据，且保持各项参数一致的条件下，本文方法具有与ACO 优化BP 算法同样的分类准确率，而经GA-ACO 优化BP 算法则达到很小误差，且可以发现CPU 处理时间更短。因此，采用GA-ACO 优化BP 算法可以同时实现故障诊断精度与收敛速率的提升。

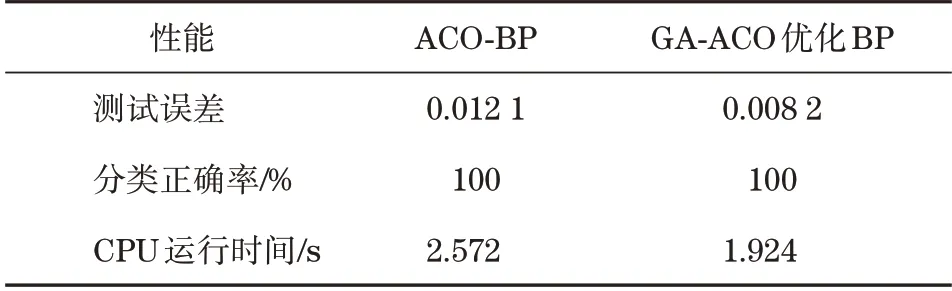
表4 性能结果比较Tab.4 Comparison of performance results

4 结论

模型实际和期望输出形成了相近的故障诊断结果，误差0.000 185，满足目标控制标准。表明对BP算法实施GA-ACO优化处理后，可以对齿轮箱故障达到很高的诊断准确率。相比较ACO 优化BP 算法，经GA-ACO优化BP算法达到很小误差，CPU处理时间更短，实现故障诊断精度与收敛速率的提升。