基于模糊可拓层次分析的梯级水库群安全评价
史 佳 枫,李 伟,朱 延 涛,徐 利 福
(1.河海大学 水利水电学院,江苏 南京 210098; 2.长江设计集团有限公司,湖北 武汉 430010; 3.流域水安全保障湖北省重点实验室,湖北 武汉 430010)
0 引 言
中国是世界上建设梯级水库群最多的国家[1],梯级水库的合理开发能提高水能资源利用率,对整个社会有着重要的经济、环境等效益,水库群的安全运行也显得尤为重要。梯级水库群是由水力联系而构成的复杂系统,任一决策调度或者环境变化都会影响流域系统内其他单元的安全性态,在实际调度运行管理中需时刻掌握系统整体以及各坝的安全性态,才能进行科学合理的调度安排。
自大坝建成之日起,其工程性态均随时间与环境影响而动态改变,在日常管理中需要对大坝的安全进行评价控制,保证工程与公共安全。流域梯级系统内各水库大坝受到不同环境因素影响,且之间互相影响互相关联,一旦受到极端风险灾害影响,极可能造成连锁反应扩大受灾范围,若处理不当,则会导致灾害效应激增,对整个流域的人民生命安全、环境安全、经济安全造成严重影响。因此,对梯级水库群进行日常的安全检查与定期的系统安全评价,对保障梯级系统工程安全与公众安全尤为重要。定期对梯级系统进行安全评价,能够及时发现并处理系统内薄弱环节,科学合理地进行补强加固,在灾害发生时有效阻断风险传播,指导安全管理以及调度工作。
目前,学者对于水库大坝的安全评价研究大多都集中于单一水库大坝,且更多针对工程本身安全进行评价,而忽略了对梯级水库群调度安全的研究。李晓璐等[2]结合层次分析法与模糊数学理论建立了多层次模糊综合评价模型,得到大坝安全综合评价的定量结果。陈曦等[3]采用多位专家评分,构建了水库大坝安全二级模糊综合评价体系,并对某农村地区水库大坝进行了安全评价。但是,这些研究大部分都侧重于定性评价方法,使得评价结果存在主观性与模糊性。
本文利用可拓层次分析法[4-5],结合模糊学理论,提出了一种基于模糊可拓层次分析的综合评价方法。以梯级水库群为研究对象,综合考虑水库群的工程安全与调度安全,建立完整的评价指标体系,利用可拓区间数建立判断矩阵确定指标权重,通过模糊隶属函数将专家评价结果定量化、模糊化,对梯级水库坝群进行综合安全评价,以期提升系统安全评价的准确性。
1 模糊可拓层次分析综合评价方法
传统的水库大坝安全评价主要以定性方法为主,存在主观性过强、局限性较大的缺点。同时,梯级水库群系统规模大、影响因素多、结构关系复杂,其安全评价指标同时具有定性因素与定量因素的特点,具有较强不确定性,不宜用传统方法进行安全评价。
层次分析法通过对定性与定量指标模糊量化,计算层次单排序与总排序,适用于多层次复杂的目标系统,在大坝安全评价中占据重要地位。但其在构造判断矩阵时忽略了人为判断的模糊性,只考虑了判断的两种极端情况,而实际情况中,人的判断往往存在一个区间,这种缺陷最终导致判断矩阵存在一致性问题[6]。一旦判断矩阵不满足一致性条件,其计算结果也失去了理论依据。可拓层次分析法结合可拓学理论与层次分析法,利用可拓学集合与物元的概念、区间数构造判断矩阵,模拟人为判断的区间,弥补了传统层次分析法构造矩阵时的极端情况,消除了度量不准确的缺点。
1.1 可拓层次分析法确定各层次因素权重
1.1.1构造可拓判断矩阵
可拓层次分析(Extension analytic hierarchy process,EAHP)法通过两两对比因素指标建立可拓判断矩阵,目的是将原始数据规范化。将因素集内的同一层次指标的重要性进行两两对比,利用可拓区间数判断其相对优劣性,构造可拓区间数判断矩阵A=[aij]n×n。
(1)
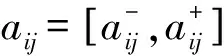
矩阵A为正反互补矩阵,因此:
(2)
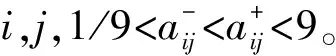

表1 1~9标度
1.1.2计算可拓判断矩阵和权重向量
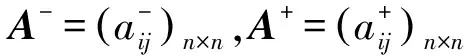
(2)计算权重系数。根据公式(3)计算可拓判断矩阵的权重系数k、m[6]:
(3)
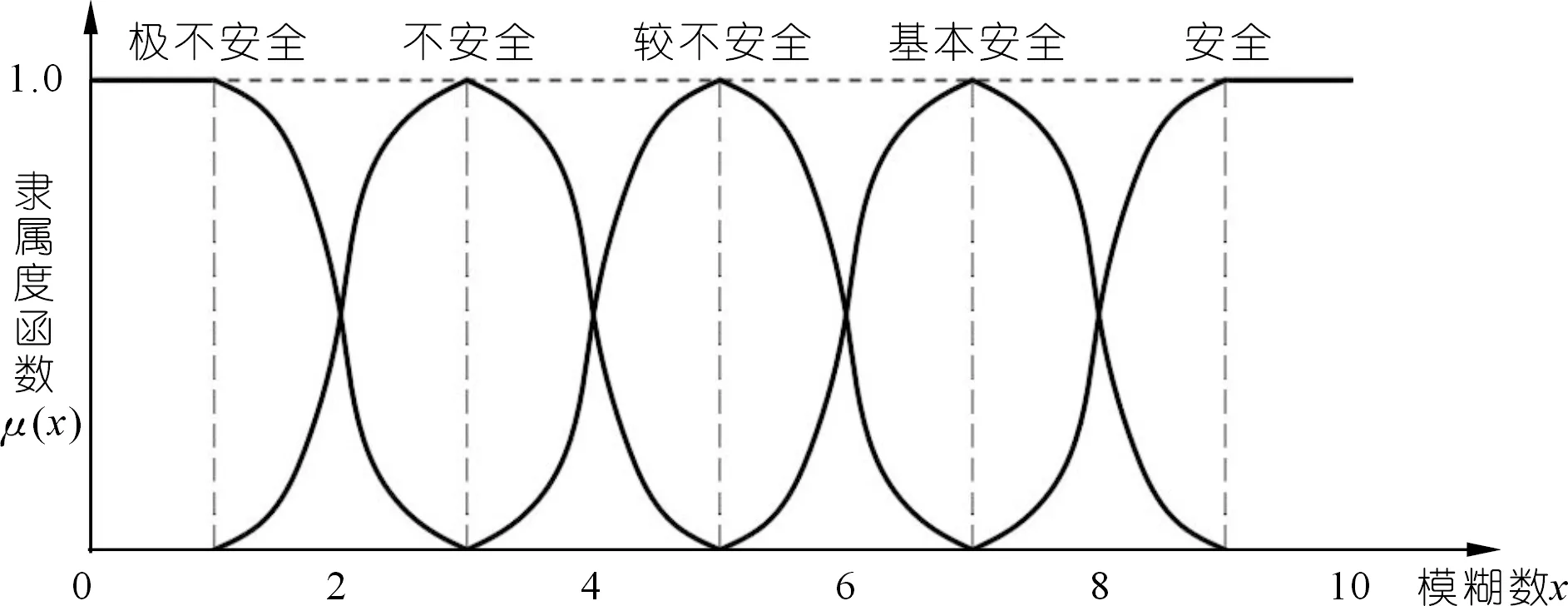
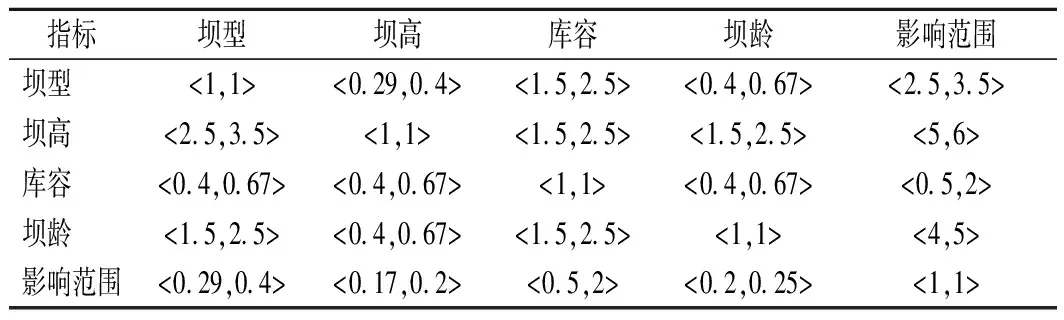
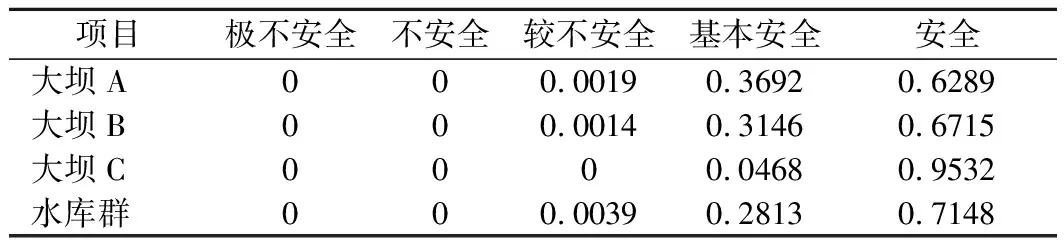
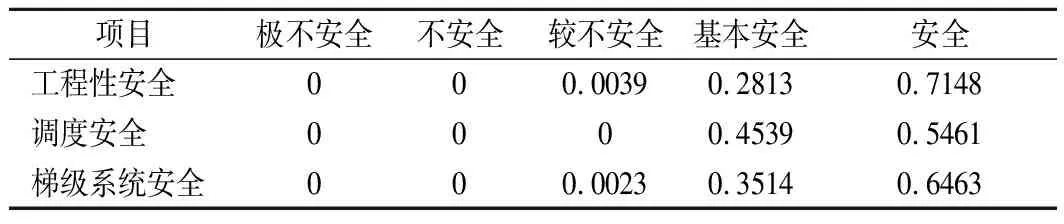
式中:k、m满足0 (3)判断矩阵一致性。由上式计算得到权重系数k、m的值,若满足0≤k≤1≤m,则表明判断矩阵一致性较好;反之,则一致性较差,需采取措施对判断矩阵进行校正或重新进行专家评审,直至满足一致性要求。 (4)求出权重向量。根据下列公式求出判断矩阵A关于特征值λ=[λ-,λ+]的特征向量,即该层次各因素指标的权重向量W[8]。 (4) 1.1.3 区间数权重单值化处理 (5) 式中:vi为第k层次中第i个指标所占的权重,经过归一化后得到的权重向量Vk=(v1,v2,…,vi)T即为该层次内各指标权重值组成的权重集。 为对水库大坝的安全性做出定量评价,根据SL 258-2000《水库大坝安全评价导则》[10]中的规定,与相关文献对梯级水库坝群系统不同安全风险状态的描述,得到其安全评价标准如表2所列。 表2 梯级水库群系统安全评价标准 由于不同指标的性质不同,对于评价指标的度量方法也不统一。表2中对于梯级水库群的定性描述只适用于部分评价指标,对于定量指标,仅通过专家对其安全状态定性描述打分过于主观片面。结合实际的监测数据,并进行计算分析,对应评判标准才能与其安全状态相关联。对此,可利用置信区间法[11],在实际监测数据的基础上,建立相对应的效应量与影响因素模型,利用效应量预测方程预测其效应量。 结合表2的安全评价标准,根据置信区间将实测效应量划分成如下5个区域: 根据实测效应量判断其所属的置信区间,得到其对应的评语集与对应的评分。 由于评价指标体系中的指标边界存在一定程度的模糊性,不同级别之间并无清晰的界限,且专家评审打分也具有主观性和不确定性。为了提高评价打分这一定性描述的准确性,本文采用模糊分布函数确定隶属度,将专家的主观意见与客观事实相结合,确定各指标的隶属度。在模糊集中,不同级别之间的边界最为模糊,中间部分相对清晰[12]。因此,本文采用岭形分布函数建立各项指标的模糊隶属函数,对评分进行模糊化处理,使专家评价更具准确性。模糊隶属函数通式如式(6)所示,其中首段采用降岭形,中间段采用窄域岭形,末段采用深岭形分布隶属函数[13]。 (6) 式中:c1、c2、c3分别为区间(u1,u2)、(u2,u3)、(u3,u4)的中值点。 根据表2中设立的评语集,将专家打分标准设置为十分制,即将对应表2中评语集的评分集定为U=(u1,u2,u3,u4,u5,u6)=(0,2,4,6,8,10),并以此构造相对应的模糊隶属函数,函数图像如图1所示。 图1 岭形模糊隶属函数 经专家打分后,将评分代入模糊隶属函数中,计算得到该层次各因素的评价模糊集μik(i=1,2,…,n,k=1~m)。 (7) 重复上述步骤,建立上一层次可拓判断矩阵,两两比较指标因素的重要性,求出权重向量,并与安全评价向量进行计算耦合,逐层计算得到最终的梯级水库群系统整体安全评价向量: M=(m1,m2,m3,m4,m5) (8) 根据表2可知,梯级水库坝群评价标准隶属度集μ={极不安全,不安全,较不安全,基本安全,安全},按照最大隶属度原则,M中最大值mi对应的隶属度评价等级,即为梯级水库坝群系统所处的安全等级。 梯级水库坝群系统安全评价是一个多层次、多因素的综合评价问题。按照梯级水库坝群系统中大坝所处位置,从上到下分别记为大坝1,大坝2,…,大坝n。对于流域内的梯级水库坝群系统安全评价可分为水库坝群工程性安全与水库坝群调度安全评价两个方面,并由此往下划分建立梯级水库坝群的层次分析结构,(见图2)。 图2 梯级水库坝群系统安全性评价指标体系 根据SL 258-2017《水库大坝安全评价导则》的内容,水库群中大坝的工程性安全可划分为工程质量评价、防洪标准复核、结构安全评价、渗流安全评价、抗震安全复核、金属结构安全以及运行管理评价七大方面,即体系中的准则层。其中七大方面又包括了诸多影响因素子集,可继续进行细部划分。如工程质量评价就包括了工程水文地质条件、工程施工质量、坝基库岸处理状况3个部分,该层次称为指标层。 由于在系统中影响大坝所占权重的因素众多,不同大坝个体之间的重要性不便于两两比较,故选取对大坝权重影响较大的坝型、坝高、库容、坝龄以及影响范围5个因素建立层次关系,根据相关安全导则制定的判断标准,通过可拓层次法进行两两比较打分,求得各大坝在系统中所占权重。 梯级水库坝群调度安全层次结构较为简单,包括了梯级预报水平、梯级调度水平、梯级预警水平3个方面。 (1)确定各水库大坝权重。梯级水库群系统中,各坝的重要程度难以直接反映。如图2所示,本文选取对大坝影响较大的5个因素“坝型、坝高、库容、坝龄、影响范围”作为指标,通过因素指标的可拓层次分析来确定各坝权重。 专家以导致大坝失事的重要程度对5个指标进行两两比较,建立可拓判断矩阵,计算指标间的相对权重,并得到单值处理后的各因素权重值。再结合梯级水库群系统安全评价标准,对比得出各坝相对安全度,分别建立梯级系统内不同因素指标下各坝安全性相互比较的可拓判断矩阵,求出其权重向量,与单因素权重综合计算,得到各坝所在梯级系统内的安全评价权重值。 (2)以梯级系统整体安全性为标准,专家对同一层次内各指标的重要性进行两两比较,得到不同层次的可拓判断矩阵,根据公式(3)~(5)计算得到各指标归一化后的权重值。 (3)专家通过现场视察、试验、计算复核等方式,结合相关实际监测数据,依据SL 258-2017《水库大坝安全评价导则》给定的各指标的安全评价方法,分别对水库坝群内各坝工程性安全的18个因素指标以及坝群调度的3个指标进行评审打分。 (4)将每个指标评分进行模糊化处理,得到各指标的模糊隶属度向量。 (5)将指标层内各指标的权重值与模糊隶属度向量计算耦合,得到准则层内各指标的安全评价向量。 (6)按照梯级水库坝群系统安全评价指标体系的层次关系,重复步骤(3)~(5),直至得到各坝的安全评价模糊隶属度矩阵。 (7)将各坝在水库群内所占的权重值与模糊隶属度矩阵计算耦合,得到水库群工程性安全评价向量;同理,可得到水库群调度安全评价向量。 (8)将梯级水库群工程性安全与调度安全的评价向量与其权重值耦合,得到梯级水库群系统安全评价集。 (9)按照最大隶属度原则,对照安全评价表标准,得出梯级水库群的安全评价等级。 流域顺流依次建有A、B、C 3座水库大坝。大坝A处于该流域支流东支河流,是一座以防洪为主,兼灌溉、发电、旅游等一体的综合性水利工程,1952年开始动工,1954年竣工。水库总库容4.96亿m3,防洪标准为1 000 a一遇。该坝为混凝土连拱坝,由20个坝垛、21个拱和两端重力坝组成,最大坝高75.9 m,坝顶高程129.96 m,水电站装机容量3.1万kW。大坝距离县城17 km,距离市区60 km,下游65 km处有公路、铁路、高铁等重要民用和军事通讯设施。大坝B处于该流域支流东支河流,与大坝A相距25 km,位于大坝A上游,两坝构成串联式梯级枢纽,是一座以防洪为主,结合灌溉、发电的水利工程,1956年动工,1968年竣工。该大坝为混凝土大头坝,该坝具有12个双支墩、两岸各3个单支墩及转折段重力坝,坝高82 m,总库容3.37亿m3,防洪标准为5 000 a一遇。该坝建成后与大坝A共同调节径流,发挥综合利用效益。大坝C处于该流域支流西支河流,位于A大坝上游,相距26 km,两坝构成串联式梯级枢纽,是一座以防洪为主,供水、发电、灌溉为辅的水利工程,2005年动工,2014年竣工。大坝为碾压混凝土拱坝,最大坝高104 m,水库总库容4.60亿m3,电站总装机容量2×25 MW。大坝C的建成,将下游大坝A的防洪标准提高至5 000 a一遇,总体上解决了其防洪标准不足的问题。 根据梯级水库坝群系统安全性指标体系及具体步骤,邀请有关方面专家进行评价打分。首先,对影响大坝的5个因素进行两两重要性比较,经专家打分后,建立可拓判断矩阵,如表3所列。 表3 大坝影响因素判断矩阵 根据公式(3)~(4),结合表3中数据计算得到其权重系数k=0.902 2、m=1.072 0,满足判断矩阵一致性要求(0≤k≤1≤m),一致性良好,并计算得到各因素指标的区间权重向量 (9) 得到各因素的权重向量W后,根据公式(5)对区间向量进行单值化处理,最终得出影响大坝的各因素的重要性比较权重为V=(0.181 5,0.406 7,0.105 9,0.258 1,0.047 8)。同理,再分别建立5个影响因素对水库坝群内各坝的可拓判断矩阵,计算得到相应单值化后的权重值,得到结果如表4所列。 表4 影响大坝安全的因素权重计算 根据步骤(1),综合表3~4中的权重值,耦合计算可得到各坝在水库群中所占的权重集为v=(0.558 6,0.203 2,0.238 3)。 根据步骤(2),对梯级水库群系统安全指标体系中,工程安全性指标层内的同层次因素指标进行重要性比较,经专家打分给出区间数,分别建立同层次内各指标的可拓判断矩阵。 再利用相关公式,得出各体系内各指标单值化后的权重向量分别为:V1=(0.022 6,0.417 1,0.560 3),V2=(0.548 8,0.410 6,0.042 7),V3=(0.867 8,0.132 2),V4=(0.031 7,0.968 3),V5=(0.031 7,0.968 3),V6=(0.022 6,0.558 9,0.418 6),V7=(0.675 5,0.258 5,0.033 4)。 同理,分别建立准则层各指标以及有关水库坝群调度指标的可拓判断矩阵,如表5所列。计算得到准则层各因素指标间的权重集为v1=(0.185 1,0.039 8,0.290 4,0.268 4,0.157 6,0.025 4,0.033 4)。 表5 准则层因素可拓判断矩阵 根据2.2节中步骤(3),利用公式(6)的岭形分布隶属度函数,将专家对3座大坝的18个指标因素评分进行模糊化处理,计算得到各评价指标的隶属度,构造评分的模糊隶属度矩阵。 根据步骤(4),利用公式(7)将各坝指标层各因素的权重值与其隶属度计算耦合,得到指标层的安全评价矩阵,该矩阵即为准则层各指标的隶属度矩阵。 根据步骤(5),将各指标的隶属度矩阵与准则层权重集计算耦合,得到准则层内各指标的安全评价向量。 根据步骤(6),分别计算各坝的安全评价向量,并进行综合计算,得到各坝的安全模糊隶属度矩阵: (10) (11) (12) 将各坝隶属度矩阵与权重综合计算,得到梯级水库坝群系统及各坝的工程性安全评价结果如表6所列。 根据表6中结果,按照最大隶属度原则对比评价集可知,该梯级水库群中的3座大坝的整体工程性态均为安全,大坝A与大坝B存在部分安全隐患;梯级系统整体也处于工程性安全状态。 表6 梯级水库群安全评价结果 根据步骤(7),对梯级水库坝群调度安全的3个指标分别进行重要性比较,建立可拓判断矩阵如表7所列。计算得到有关水库坝群调度安全的3个指标的相对权重集v2=(0.105 9,0.587 1,0.307 0)。利用模糊隶属函数将专家打分模糊化后得到各指标的隶属度矩阵,将权重集与隶属度矩阵计算耦合,得到水库坝群调度安全的综合评价向量E=(0,0,0,0.453 9,0.546 1)。 表7 梯级水库群调度安全可拓判断矩阵 根据步骤(8),建立梯级水库坝群系统安全评价判断矩阵如表8所列,计算得到有关梯级水库坝群系统安全评价两个方向的相对权重v=(0.594 0,0.406 0)。将权重向量与其综合安全评价矩阵计算耦合,得到最终的系统安全评价如表9所列。 表8 梯级水库群系统可拓判断矩阵 表9 梯级水库坝群系统综合安全评价 根据步骤(9),按照最大隶属度原则,查表可得该梯级水库坝群的工程性安全与调度安全均处于安全状态,整体的梯级系统也处于安全状态。 运用传统的层次分析法对该梯级水库群进行安全评价,比较两种方法的评价结果。由表10可知,其所得结果相一致,且均符合该梯级水库坝群的实际运行安全状况,证明了该方法的合理性。同时,相较于AHP法,本文中使用的EFAHP法不需进行大量的计算验证一致性,提高了计算效率,且评价结果偏安全,更为合理。 表10 不同安全评价方法结果比较 本文针对传统层次分析法存在的人为判断极端性导致结果不准确的缺点,结合梯级水库群规模大、影响因素多、结构关系复杂的特点,提出了模糊可拓综合层次分析法。首先,从梯级水库坝群工程性安全与调度安全两方面入手,改进了单一水库的安全评价体系,综合考虑了影响梯级系统整体安全的复杂结构,建立了梯级水库坝群安全指标体系,使得评价指标体系更贴近实际情况。引入可拓区间数优化判断矩阵,改进了指标权重的确定,在计算过程中同时检验其一致性,较传统的权重计算更加简便准确。通过岭形分布模糊隶属函数对专家打分模糊化,清晰化不同评价级别边界,提高了系统安全评价的合理性与准确性,使得整体评价更具客观性。通过3级串联水库群工程实例,验证了模糊可拓层次分析评价法对于水库坝群安全状态评价的合理性与准确性。该方法提高了掌握水库大坝整体安全状态的准确性,适用于梯级库群日常运行安全管理与定期检查报告,可发现系统内薄弱环节并提出必要的改进建议,为梯级库群日常养护修理、经费安排以及合理管理调度提供了科学依据。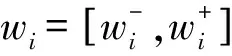
1.2 确定评语集
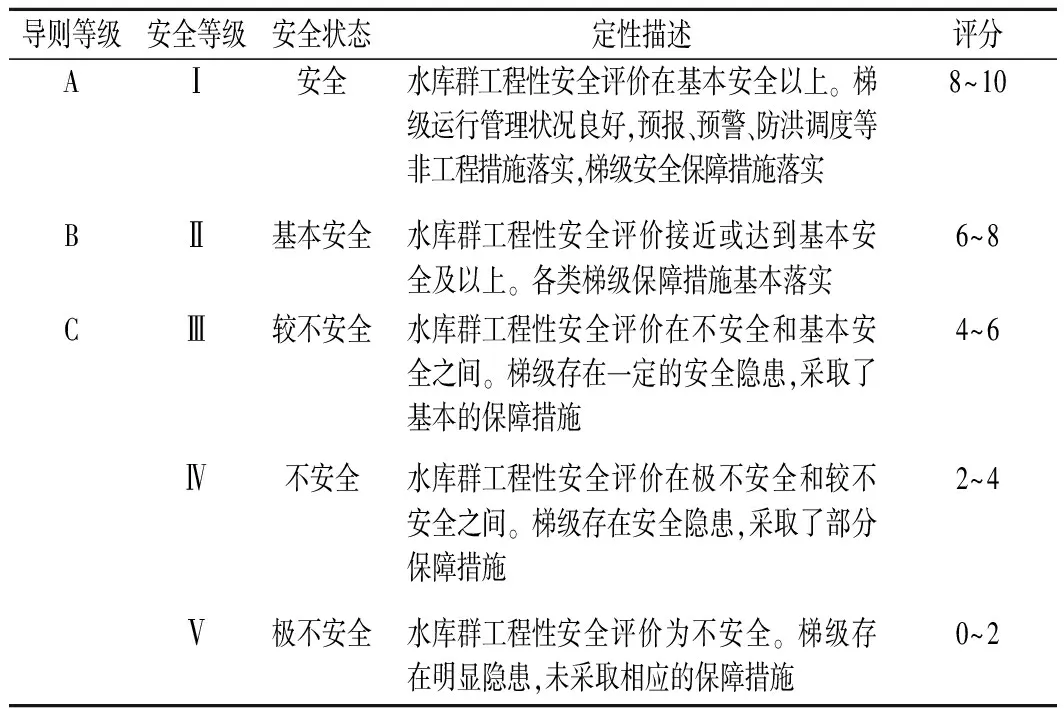
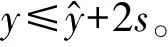
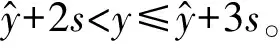
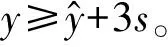
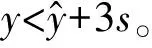
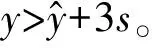
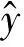
1.3 评分模糊化处理
1.4 系统安全综合评价
2 梯级坝群安全指标体系及具体评价步骤
2.1 建立层次结构模型

2.2 具体步骤
3 工程实例验证
3.1 工程概况
3.2 评价结果





4 结 语

