基于转动惯量辨识的PI控制器参数自整定

丛峰武 傅国辉 李熙然 徐振兴

1.鞍山钢铁集团有限公司齐大山选矿厂；2.大连交通大学

巡检机器人运动控制系统中，交流伺服系统的控制性能直接影响机器人系统运动的稳定性，而电机结构参数中转动惯量对系统性能的影响最为显著。本文先采用扩展卡尔曼滤波器算法对电机转动惯量进行辨识，在辨识结果基础上，根据最佳系统设计法，在保证系统快速响应能力和强抗干扰性的原则下，得出速度环PI控制器比例增益随转动惯量作线性调整时能够满足系统控制要求。

近年来，变频调速技术发展迅速。永磁同步电机因其结构简单、平均效率高、体积小、重量轻、调速范围大等优点，成为伺服系统动力输出的重要驱动模块，但是其缺点同样明显。首先，当外界温度过高或者过低时，电机可能会发生失磁现象，使得电机性能下降甚至损坏，影响伺服系统的控制性能。其次，当永磁同步电机长时间运行时，电机结构的参数会随时间产生变化，电机转轴的转矩输出特性也随着负载的频繁变化而降低。为了解决此问题，同步获取电机参数的变化，并且根据变化的参数调整控制器内部增益或给出补偿，能缓解参数变化给伺服系统控制效果带来的影响[1]。目前工程应用中的伺服器多采用人工手段对控制器参数加以调整，该方法要求工作人员有极高的专业知识储备和丰富的调试经验。为了保证控制效果，当改变电机负载之前，都需要调整控制器参数，这会增加生产成本和延长制造周期[2]。这些因素极大地影响了伺服控制技术的发展与推广。

1 系统整体方案设计

永磁同步电机具有复杂性、非线性、强耦合等特性[3]，为精确控制伺服电机的速度，在中小功率的伺服系统中，通常采用直轴电流为零的转子磁场定向矢量控制策略[4]。为了实现解耦控制，系统采用电流环与速度环双闭环反馈控制策略，近似解耦方式的反馈解耦能够得到良好的动静态性能，能高精度线性控制电机转矩，达到近似解耦控制的目的，如图1所示为系统设计方案的整体结构框图。

图1 系统整体结构框图Fig.1 System overall structure block diagram

2 转动惯量辨识

转动惯量的变化会直接影响系统的控制性能[5]，对系统性能调节的前提和依据是在线监测转动惯量的变化趋势。本文采用基于扩展卡尔曼滤波器的电机转动惯量辨识算法，在电机低频转速时，能实时监测电机速度状态，并能估计负载状态和某些参数[6]。

扩展卡尔曼滤波器主要包括状态预测和校正反馈两个阶段，预测过程为时间更新过程，校正过程为测量更新过程。预测过程中，在k时刻状态估计x^ (k)，利用系统的状态微分方程可预测k+1时刻的状态，先验估计值x^ (k+1)[6]；校正过程中，以实测值来校正经过上一步预测得到的状态先验估计值，其递推流程如图2所示。

图2 扩展卡尔曼滤波器辨识流程Fig.2 Extended Kalman filter identification

将永磁同步电机的机械运动方程改写为如式（1）所示：

在永磁同步电机伺服控制系统中，可测量输出转矩和转子机械角速度，因此B=0，T为卡尔曼滤波器的采样周期，可将永磁同步电机的机械运动方程和输出方程如式（2）、式（3）所示的状态方程表示：

对上述方程进行离散化，可得系统的梯度矩阵如式（4）所示：

变换矩阵如式（5）所示

根据迭代方程及系统状态方程，可得扩展卡尔曼滤波器辨识算法，算法流程为在辨识子程序运行前对系统进行初始化，包括电机特性参数、算法采样周期、仿真总时长等。设定仿真的采样周期为0.0001s，采样时长为0.6s，状态变量初值x(0)经对次仿真验证选取10-6kg·m2，估计噪声协方差矩阵初值P(0)取为diag(1,1,10)，测量噪声的协方差矩阵初值R(0)取为0.05。因为电机速度发生变化时辨识才有意义，仿真时设转速幅值为200r/min和300r/min，其变化频率为25Hz，并添加电机在运行过程中外部扰动引起的噪音，即转速振荡。当电机空载启动时，转动惯量的输出值即为电机本身的转动惯量，其转动惯量的辨识输出曲线如图3所示。

图3 扩展卡尔曼滤波器惯量辨识结果曲线Fig.3 Curve of extended Kalman filter inertia identification result

转动惯量的辨识结果曲线可知：辨识结果在0.32s时接近真实值，稳态时惯量输出值为0.0007974kg·m2，其误差为0.33%，是在误差允许范围之内。以给定方波脉冲转速模拟外部扰动引起的电机转速变化时，转动惯量输出曲线、转速输出曲线变化频率相同频率，最大误差不超过1.5%。在惯量不发生变化时，辨识算法在外部干扰作用下，其输出能够保证较高精度，对于复杂时变系统有着很强的跟踪特性，满足参数自整定需要。

3 控制器参数自整定

根据伺服系统控制器参数整定得先内环后外环的原则，先对电流环进行整定。两个电流环控制器通结构设计相同，因此选择转矩电流环作为研究对象[7]。其中电流环的开环传递函数如式（6）所示：

其中，Ti为积分时间常数，Tif为反馈滤波时间常数，Ki为电流环PI控制器比例增益；KPWM为逆变器放大系数，TPWM为逆变器时间常数，它们的取值与IGBT开关频率有关；Ra为电枢绕组等效电阻，La为电枢绕组等效电感，Ka为电流检测反馈增益。

电流环PI控制器整定后比例及积分常数如式（7）所示：

根据上式分析可得，电流环控制器参数通常与伺服系统本身的结构有关。

速度环的开环传递函数如式（8）所示：

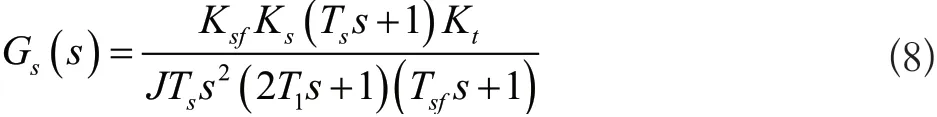
速度环PI控制器比例及积分常数的整定结果如式（9）所示：

根据上式可得，速度环PI控制器积分时间常数通常与伺服系统本身的结构有关，而比例增益要随转动惯量作线性调整，以补偿因转动惯量变化带来的系统性能下降。

电机转动惯量变化范围设置为从无负载状态至初始转动惯量值的10倍，递增步长为0.0008kg·m2，记录每次比例增益调整值，如表1所示为其输出结果。

表1 速度环比例增益与转动惯量变化关系Tab.1 Relationship between proportional gain of speed loop with the moment of inertia

将速度环比例增益与对应时刻的转动惯量进行线性拟合，拟合曲线如图4所示，两者之间可在线建立线性正比关系，拟合曲线的确定系数为1，验证了算法设计的有效性，自整定控制算法的输出结果能够对转动惯量的变化进行动态跟踪，并实时做出相应的调整。

图4 速度环比例增益与转动惯量拟合曲线Fig.4 Fitting curve of velocity ring proportional gain and moment of inertia

设定电机给定转速为1000r/min，施加1N·m的负载转矩，在0.1s时突加负载转矩，此时负载转矩为5N·m，转速及电磁转矩的输出曲线分别如图5和图6所示。

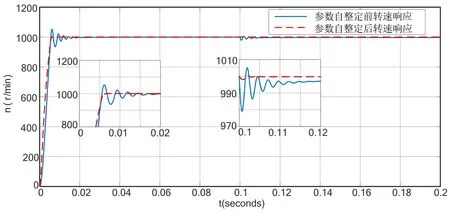
图5 两种控制模式下电机转速仿真曲线Fig.5 Simulation curves of motor speed under two control modes

图6 电磁转矩输出曲线Fig.6 Electromagnetic torque output curves

如图5所示，参数整定前PI控制器控制转速时，其最大超调量达到6.7%，转速超调量大，多次振荡后趋于稳定，稳态时间为0.022s，调节到稳态得时间过长，振荡次数过多，使电机在运动过程中发生抖动现象，长时间处于非平稳启动状态容易毁坏电机[7]；转动惯量辨识的PI自整定控制方式，转速响应快，超调量小，调节时间比整定前下降61%。在电机运行过程中加负载转矩时（0.1s），整定前转速会下降约给定转速的1.1%，影响电机平稳工作；反而整定之后施加负载，电机在外部干扰下其转矩下调量为0.1%左右，电机能稳定运行。

如图6所示，控制器参数整定前电机在启动阶段转矩产生振荡，增加电机能耗，稳定性降低，产生冲击电流，影响电枢绕组，严重时电机会烧毁。当扰动发生（增加负载转矩）时，电磁转矩也会发生轻微脉动，对外部负载的干扰也比较敏感。参数自整定后，启动阶段转矩比较平稳、电流超调较小，在外部扰动的情况下，转矩接近无抖动状态，系统的抗干扰能力显著提升。

4 结论

本文主要研究了基于扩展卡尔曼滤波器的转动惯量在线辨识方法，基于此种辨识方法实时监测转动惯量的变化趋势，以此为依据设计了交流伺服系统电流环与速度环控制参数整定方案，并在上位机进行系统仿真，得到如下结论：

（1）转动惯量辨识速度快，在0.32s辨识输出曲线趋于收敛，稳态误差为0.33%，在受到外部扰动时的最大误差不超过1.5%。

（2）参数自整定后，系统在启动阶段转速超调量有明显下降，调节时间降低61%，且启动电流更小；在突加负载时，转速脉动降低1%，转矩实现了无抖动调节。

引用

[1]陶涛,林荣文,李伟起.基于蚁群算法的交流永磁伺服系统控制器参数寻优研究[J].电气开关,2020,58(3):64-69.

[2]ZHENG W J,LUO Y,CHEN Y Q,et al.A Simplified Fractional Order PID Controller's Optimal Tuning:A Case Study on a PMSM Speed Servo[J].Entropy,2021,23(2):130.

[3]杨晓辉.数控机床中永磁同步电机非线性混沌同步控制算法的研究[D].南昌:南昌大学,2016.

[4]王子昭,费骏韬,史林军,等.永磁同步电机电流控制策略比较分析[J].电机与控制应用,2019,46(5):64-71.

[5]徐勇.交流伺服系统控制器在线参数自整定方法[J].电机与控制应用,2017,44(6):45-50.

[6]贾勇.交流伺服系统PI控制器参数自整定方法研究[D].大连:大连交通大学,2018.

[7]陈鹏展.交流伺服系统控制参数自整定策略研究[D].武汉:华中科技大学,2010.